类电磁机制算法求解模糊流水车间调度问题＊

邵 扬 王晓娟

（武汉理工大学物流工程学院 武汉 430063）

0 引 言

很多调度优化问题都针对的是静态环境下的，但是实际生产过程中，由于设备、环境和人为因素的影响，工件的加工时间、交货期等参数通常是不确定的值.不确定环境下的流水车间调度问题（flow shop scheduling problem，FFSP）已经引起了国内外一些学者的关注，Balasubramanian和Grossmann［1］提出了一种新型的分支定界方法求解了加工时间不确定的流水车间调度问题，Nezhad和Assadi［2］提出了一种改进的CDS算法求解了模糊流水车间调度问.Javadi等［3］针对多目标无等待的流水车间调度问题提出了一种模糊多目标的线性规划模型.Hong和Wang［4］研究了加工时间不确定的柔性流水车间调度问题.Wu［5］给予遗传算法求解了加工时间和交货期不确定的流水车间调度问题.类电磁机 制（electromagnetism－like mechanism，EM）算法由Birbil在2002 年提出［6］，是一种基于群体的全局优化算法，它通过模拟电磁场中的吸引－排斥机制，来实现对全局最优值的搜索.该算法已在函数优化［7］、神经网络训练［8］等优化问题中获得成功应用.本文采用模糊数来表示不确定的加工时间和交货期，通过引入随机键的表达方式，采用了EM 算法对模糊流水车间调度问题进行了求解.

1 类电磁机制（EM）算法简介

1.1 EM 算法的基本原理

类电磁机制算法是一种基于种群的优化算法，将每个解比作一个带电粒子，每个粒子的电荷的多少由该粒子对应的目标函数值确定，而电荷的多少决定了该粒子对种群其他粒子的吸引或者排斥的强弱，目标函数值越优，吸引或排斥力就越大.然后通过吸引或排斥力确定每个粒子下一步的移动方向，使搜索粒子都向着较优解所在区域移动.

1.2 EM 算法的基本步骤

EM 算法主要由4个基本步骤组成：初始化、局部搜索、计算合力和移动粒子.下面以函数优化为例，介绍该算法的基本步骤，求目标函数f（x）在可行域中的最小值.

1.2.1 初始化 从已知可行域中随机选取m 个点作为初始粒子，然后计算出每个粒子的目标函数值f（xi），并将目标函数值最优的粒子记为xbest，也称其为当前最优粒子.

1.2.2 局部搜索 局部搜索主要用来在单个粒子的领域范围内改进当前种群已搜索到的解.实验表明，当只对当前最优粒子进行局部搜索时，能较好地维持速度和精度的平衡.

1.2.3 计算每个粒子的合力 首先根据每个粒子的目标函数值计算每个粒子所带的电荷量，电荷的计算公式为

然后计算作用在粒子i上的合力Fi，根据下式计算.

根据这个公式，目标函数值较优的粒子将拥有较大的电荷数，具有更强的吸引或者排斥力力；另外，目标函数值较优的粒子将吸引其他粒子，反之，目标函数值较差的粒子将排斥其他粒子.

1.2.4 移动粒子 粒子i将沿着合力Fi的方向移动，步长λ为一个在［0，1］上均匀分布的随机值.在式（3）中，RNG 为一个向量，其分（向）量表示对应的朝上边界uk或者下边界lk移动的可行步长.粒子每一步移动为：

2 模糊数相关理论

2.1 模糊数和操作

本文用模糊数来表示不确定的加工时间和交货期，用三角模糊数表示不确定的加工时间，三角模糊数如图1所示.用梯形模糊数来表示不确定的交货期，如图2所示.

图1 三角模糊数

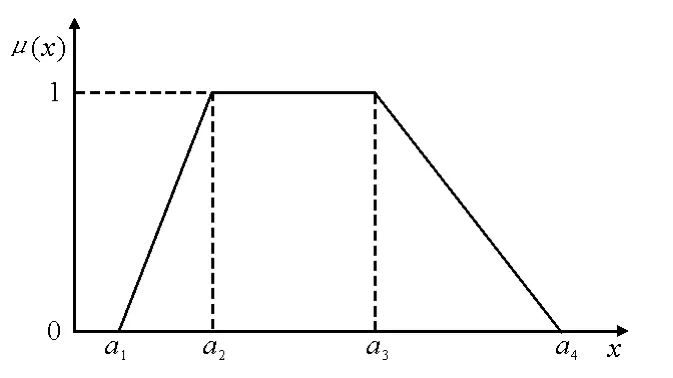
图2 梯形模糊数

模糊调度问题中，模糊数的操作是很重要的问题，它包括模糊数的求和、取大以及模糊数的比较.

1）求和 对于三角模糊数和梯形模糊数，求和操作为

2）取大 三角模糊数的取大操作为

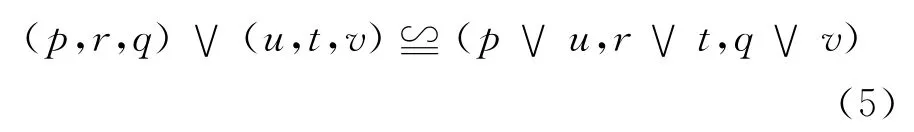
2.2 模糊数的比较

模糊数间的比较操作，采用Sakawa等人提出的准则进行［9］.

3 EM 求解模糊流水车间调度问题

3.1 优化目标

1）最大化平均满意度

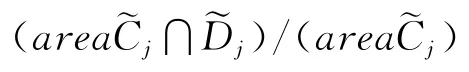
图3 满意度（AI）

2）最小化最大模糊完工时间

3.2 求解流程

通过引入随机键的编码方式，将离散型的工件排序编码转换成能用EM 算法直接求解的连续型编码.基于EM 的模糊流水车间调度算法的步骤如下.

步骤1 将每个粒子通过随机键的编码方式映射成调度问题的一个解，初始化粒子.

步骤2 利用模糊数的求和与取大操作，计算出各粒子的目标函数值.

步骤3 进行局部搜索.

步骤4 根据式（1），（2）计算合力.

步骤5 根据式（3）计算位移，移动粒子.

步骤6 若算法达到最大迭代次数，则算法停止；否则，返回步骤2继续迭代.

4 测试与结果比较

1）最大化平均满意度 本文采用了文献［10］和［11］中的测试实例，以最大化平均满意度为优化目标进行了测试，结果如表1所列，与文献中的结果相比，本文的测试结果要优.

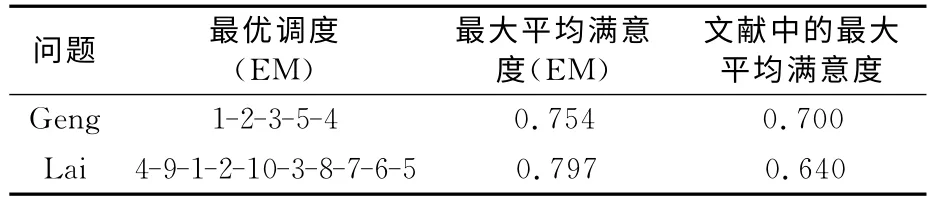
表1 文献［10］和［11］中的实例测试结果

2）最小化最大模糊完工时间 在以最小化最大模糊完工时间为优化目标的测试里，采用了文献［12］，［13］和［14］中的实例进行测试.因为文献［13］和［14］中的问题是无等待模糊置换流水车间调度问题，所以这里只是用到了文中数据，未对结果进行比较.EM 算法的参数设置如下：种群数为20，算法的迭代次数为100，测试结果如表2 所列.

表2 文献［12］，［13］和［14］中的实例测试结果

为了测试算法的收敛速度，这里给出了迭代次数和目标函数值之间的关系，依次如图4所示，从图4可以看到，针对这3个问题，本算法都有较快的收敛速度，针对文献［12］和［13］中的问题，当迭代次数在10左右时，算法就已经收敛.对于文献［14］中的问题，当迭代次数不到30时算法也已收敛.

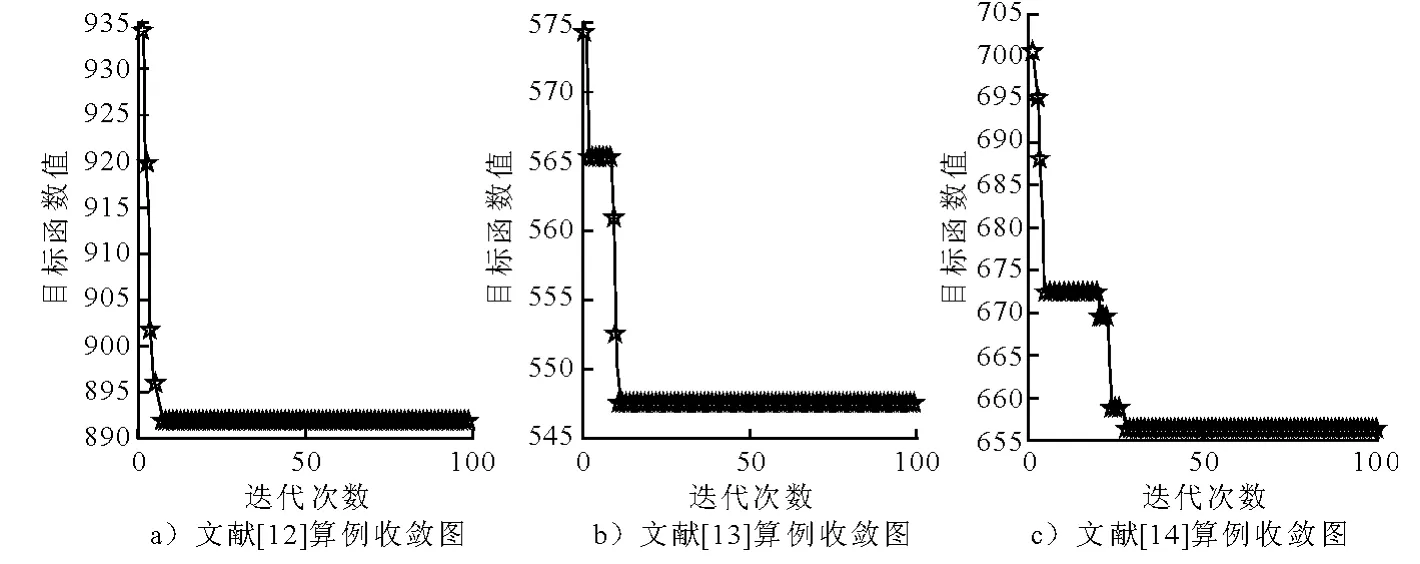
图4 文献［12］，［13］，［14］中算例的收敛图

5 结束语

本文通过引入随机键的方法，采用了一种元启发式算法——类电磁机制（EM）算法求解了模糊流水车间调度问题，优化目标有最大化平均满意度和最小化最大模糊完工时间.测试实例和结果显示，类电磁机制算法能较好地求解模糊流水车间调度问题.在以后的研究中，将采用更多的测试实例进行验证，并进一步提高EM 算法的优化性能.

［1］BALASUBRAMANIAN J，GROSSMANN I E.A novel branch and bound algorithm for scheduling flowshop plants with uncertain processing times［J］.Computers and Chemical Engineering，2002，26（1）：41－57.

［2］NEZHAD S，ASSADI R.Preference ratio－based maximum operator approximation and its application in fuzzy flow shop scheduling［J］.Applied Soft Computing，2008，8（1）：759－766.

［3］JAVADI B，MEHRABAD M S，HAJI A，et al.No－wait flow shop scheduling using fuzzy multi－objective linear programming［J］.Journal of the Franklin Institute，2008，345（5）：452－467.

［4］ HONG Tzungpei，WANG Tzutin.Fuzzy flexible flow shops at two machine centers for continuous fuzzy domains［J］.Information Sciences，2000，129（1－4）：227－237.

［5］WU Hsienchung.Solving the fuzzy earliness and tardiness in scheduling problems by using genetic algorithms［J］.Expert Systems with Applications，2010，37（7）：4860－4866.

［6］BIRBILŞ˙I.Stochastic global optimization techniques［D］.Raleigh Thesis：North Carolina State University，NC，USA，2002.

［7］BIRBILŞ˙I，FANG S C.An electromagnetism－like mechanism for global optimization［J］.Journal of Global Optimization，2003，25（3）：263－282.

［8］WU Peitsang，YANG Wenhung，WEI Naichieh.An electromagnetism algorithm of neural network analysis－an application to textile retail operation［J］.Journal of the Chinese Institute of Industrial Engineers，2004，21（1）：59－67.

［9］SAKAWA M，KUBOTA R.Fuzzy programming for multi－objective job shop scheduling with fuzzy pro－cessing time and fuzzy duedate through genetic algorithm［J］.European Journal of Operational Research，2000，120（2）：393－407.

［10］GENG Zhaoqiang，ZOU Yiren，Using genetic algorithm to solve fuzzy flow－shop scheduling problem［J］.Systems Engineering and Electronics，2002，24（6）：5－7.

［11］LAI Pengjen，SHU Minghung.Tardiness in fuzzy flow shop scheduling problems based on possibility and necessity measures［J］.Eighth International Conference on Intelligent Systems Design and Applications，Kaohsiung City，Taiwan，2008（26－29）：437－441.

［12］XU Zhenhao，GU Xingsheng.Flow shop scheduling problems under uncertainty based on fuzzy cut－set［C］∥International Conference on Natural Computation，Changsha，China，2005：880－889.

［13］徐震浩，顾幸生.不确定条件下具有零等待的流水车间免疫调度算法［J］.计算机集成制造系统，2004（10）：1247－1251.

［14］郑 璐，顾幸生.含零等待模块的存储时间有限型混合模糊Flow shop生产调度问题［C］∥第五届全球智能控制与自动化大会会议论文集（4），2004：2909－2913.