飞行冲突解脱与恢复几何模型及管制策略＊

朱承元 孟 旭

（中国民航大学空中交通管理学院 天津 300300）

目前空中交通仍然采用集中式管制方法［1］，由管制员负责航空器飞行的统一指挥、调度与决策.由于采用大量先进的通信、导航与监视设备，未来飞行需要提高航空器保持自主飞行间隔的作用，需要飞行员与管制员的协同工作和融合［2］.

近年来，国内外学者采用多种方法解决来研究这一问题，如遗传算法［3－4］、蚁群算法［5］、神经网络［6］、对策理论［7］、图论［8］及半定规划等［9］.本 文重点在于保证到达目标点的预计到达时间（ETA）不变的限制条件下，研究几何最优和两次机动（解脱机动和恢复机动）下2航空器间的飞行冲突解脱模型和飞行恢复几何模型.不仅研究了适合飞机机载计算机和管制自动化系统计算机的解脱与恢复算法，还研究了适合于管制员进行人工飞行解脱与恢复的管制策略.

通用符号规则说明：s为航空器位置变量；v为航空器速度变量；t为时间.s或v 下标中含o为本机的位置或速度变量；s或v 下标中含i为入侵机的位置或速度变量；s或v 下标不含o或i为两机相对位置或速度变量，s或v 下标中含x，y或z 表示在相应轴上的位置或速度坐标分量.解脱段所涉s或v 变量上标加一撇，恢复段所涉s或v 变量上标加两撇.其余变量在文中说明.

1 冲突解脱与恢复过程

采用三维笛卡儿坐标，z 轴垂直向上，如图1所示.入侵机位于原点，本机相对位置s＝so－si，相对速度v＝vo－vi.其中s＝（sx，sy，sz）；so＝（sox，soy，soz）；si＝（six，siy，siz）；vo＝（vx，vy，vz）；vo＝（vox，voy，voz）；vi＝（vix，viy，viz）.入侵机保护区：P＝｛（x，y，z）｜x2＋y2＜D 且｜z｜＜H｝.其中D 为保护区半径；H 为保护区的高度.若s＋tv∈P 则可以判明航空器之间存在冲突.

假设入侵机一直保持原有飞行，由本机进行冲突解脱和恢复机动.为使机动数最少，本机仅执行解脱机动和恢复机动这2次机动.机动航迹分解为解脱航迹和恢复航迹2个直线航迹，如图1所示.t′为转换时间；t″为预计到达时间.

图1 解脱－恢复机动过程

若解脱航迹和恢复航迹与入侵机保护区相切，不仅可以满足冲突解脱与恢复限制要求，同时使整个机动距离最短且本机所需做出的机动数最少.本文考虑单环形和解脱－环形两种垂直机动情况，入侵机处于平飞状态.单环形情况，解脱和恢复航迹分别切圆柱形保护区上（下）底面圆环和上（下）底面圆环且不穿透保护区侧面，适合于本机处于平飞状态；解脱－环形情况，仅有解脱航迹切圆柱形保护区上（下）底面圆环且不穿透保护区，适合于本机处于爬升或下降状态.

2 解脱与恢复模型

2.1 解脱与恢复时间

在限定条件下通过解全系数二次方程求出解脱和恢复时间可行解.

2.1.1 航空器水平接近时间 2航空器水平飞行状态情况下，即vz＝0，本机相对位置s＋tv，若其与保护区P 相交，有

化简为t的二次方程，得到判别式Δ

若Δ＞0，与保护区有2个交点，称Θ′为进入点时间，Θ″为离开点时间.

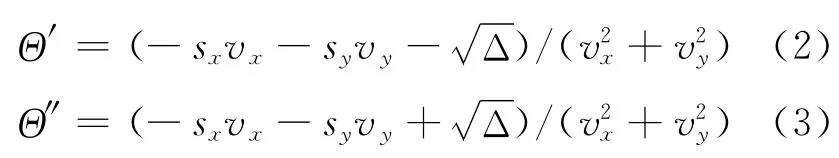
若解脱航迹与恢复航迹分别与保护区侧面相切，则到达2个切点的时间分别为

2.1.2 到达高度H 和－H 的时间 本机相对入侵机有高度变化，即vz≠0，本机到达保护区上圆环H 或下圆环－H 的时间分别为

2.1.3 转换时间 为保证预计到达时间不变，解脱航迹转移到恢复航迹的转换点的转换时间t″要满足下列向量关系

式中：t″为预计到达时间.

2.2 仅改变垂直速度的解脱恢复策略

2.3 仅改变地速的解脱恢复策略

设解脱恢复阶段水平方向地速改变倍数k，j＞0，垂直速度不变.本机在解脱恢复阶段地速改变关系

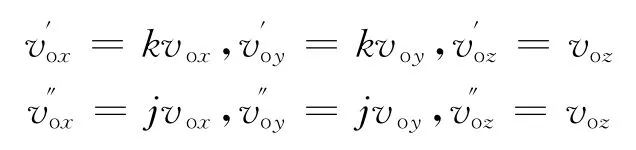
绝对地速不为0，易证k≠j且（k－1）（j－1）＜0.解脱恢复策略目的是确定t′，k 和j.转换时间t′由式（8）可得.

解脱恢复阶段水平方向地速改变倍数k，j按下式确定.

2.3.1 单环形 解脱航迹在Γ′时与环形相切，由（6）式求Γ′并验证0＜Γ′＜t″，有等式

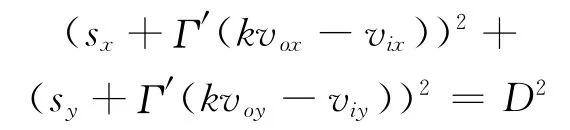
求k.式（9）求t′，验证Γ′＜t′.

恢复航迹与环形在Γ″时相切，据式（7）求Γ″并验证0＜Γ″＜t″满足，有

从中求得j.式（9）求t′，验证t′＜Γ″.

2.3.2 解脱－环形

0＜Γ″＜t″，由式（10）求j，t′＝Γ′，解式（9）得

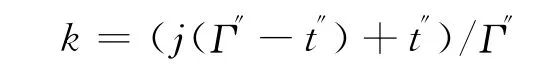
2.4 改变航向的解脱恢复策略

改变航向的方法在解脱段只改变航向，恢复段不仅改变航向还要改变地速.满足

2.4.1 单环形 验证0＜Γ′＜t″，解脱段满足：

验证τ′＜Γ″＜t″.在Γ″时刻，航空器之间水平距离为D：

从中求t′.继而解得

2.4.2 解脱－环形 验证0＜Γ′＜t″，解脱段满足：

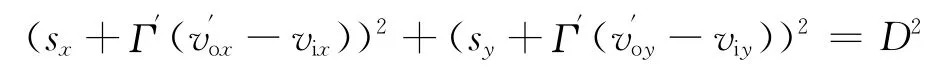
从式（8）推导出恢复段的速度，即：

3 仿真分析

3.1 单环形解脱恢复策略

2机同高度层平飞，本机速度vo＝（Vosinα，Vocosα，0），km／h，入侵机 速度vi＝（Visinβ，Vicosβ，0），km／h.α和β 分别为本机和入侵机的飞行航向.决策时间t（定义为本机预计到达入侵机保护区边缘的时间）为10min.保护区半径为10 km，高度为0.3km.研究使用单环形解脱与恢复策略时不同地速和不同航向角差（α－β）条件下的转换时间t′变化.设入侵机向东飞行，β＝90°不变，分别取α－β＝0°（同向飞行），45°，90°，135°，180°（对头飞行），计算结果见表1～表3.计算还表明，无论vo，vi及其航向夹角如何变化，解脱段爬升垂直速度和恢复段下降垂直速度均为0.5m／s.

表1 2机航向角差α－β＝45°／90°／135°时对应的转换时间t′ s

表2 2机对头飞行（α－β＝180°）时对应的转换时间 s

表3 2机同向飞行（α－β＝0°）时对应的转换时间t′ s

由表1观察分析可知，在2机飞行航向角固定的情况下，本机或者入侵机飞行速度大时，转换时间t′均减小.在2机飞行速度相对固定的情况下，航向角差大时，转换时间t′小.当2机航向差45°、速度均为300km／h时，转换时间t′为最大757s；当2机航向差135°、速度均为1000km／h时，转换时间t′为最小625s.因此可见，在一般民航客机速度范围内，2机不同地速和航向的配对情况下，使用单环形解脱与恢复策略时转换时间t′区间为757～625s.表2反映出在2机对头飞行时，2机速度之和越大，转换时间越小.转换时间t′区间为660～630s.对于这2个表格中所有情况选取t′＝757s均可以满足解脱与恢复的要求.表3提供了2机同向飞行，本机处于追赶情况下转换时间随2机速度差变化的关系.上述表格，给出了2机不同速度不同航向下采用单环形解脱恢复策略时转换时间在极限情况下的数量关系，实际管制应用中管制员需要在上述表格基础上给出安全裕量.

3.2 解脱－环形解脱恢复策略

考虑本机在爬升过程中与平飞入侵机产生的冲突，设本机爬升率为8km／h，即2.2m／s.本机速度vo＝（Vosinα，Vocosα，8）km／h，入侵机速度vi＝（Visinβ，Vicosβ，0）km／h.α和β 分别为本机和入侵机的飞行航向.保护区半径为10km，高度为0.3km.决策时间t为10min.设入侵机向东飞行，β＝90°不变.航向角差选取α－β＝0°（同向飞行），45°，90°，135°，180°（对头飞行）5种情况.在此讨论在一般民航客机速度范围内不同地速及其航向角差对解脱－环形解脱与恢复策略的影响.

用解脱－环形策略计算可得，无论vo，vi及其航向夹角如何变化，转换时间相同，均为600s.本机和入侵机不同地速和不同航向差条件下采用解脱－环形策略所需的垂直速度如表4.

表4 爬升与平飞交汇解脱－环形所需爬升垂直速度策略

表4 中“其他”一栏是在2 机速度为300，500，800，1000km／h和航向角差45°，90°，135°，180°时不同配对组合下计算结果经分析、简化综合而成，是最保守的解脱恢复策略，可以满足不同配对组合下的所有情况.表4可看做是一张人工调配管制策略表，给出了本机爬升率为2.2 m／s时的解脱－环形的解脱恢复策略.表中数据均为切保护区边界的极限情况.实际应用中应视具体情况对其放宽处理，给予适当的安全裕量即可.

4 结束语

本文从几何最优和机动数最少的角度，研究了在保证到达目标点的预计到达时间不变下垂直机动的冲突解脱与恢复模型.大量仿真研究证明了其模型的有效性.在该模型仿真的基础上，根据冲突两机不同的飞行速度和航向角的配对组合，进行综合归类简化得到了管制决策时间10min的解脱与恢复策略表.该策略表反映了切保护区边界的极限情况下的解脱与恢复策略，可直观指导管制员进行两机飞行冲突的管制决策工作.

［1］PERRY T S.In search of the future of air traffic control［J］.IEEE Spectrum，1997，34（8）：18－34.

［2］林 红，王 璇.未来的空中管制飞行［J］.中国民用航空，2009（5）：33－37.

［3］刘 星.遗传算法在飞行冲突探测解脱中的应用［J］.南京航空航天大学学报，2002，34（1）：67－71.

［4］杨尚文，戴福清.基于一种免疫遗传算法的自由飞行冲突解脱［J］.航空计算技术，2007，37（1）：45－49.

［5］郭 茜，聂润兔，王 超.多机飞行冲突解决方法研究［J］.武汉理工大学学报：交通科学与工程版，2010，34（3）：460－463.

［6］DURAND N，ALLIOT J M，MEDIONI F.Neural nets trained by genetic algorithms for collision avoidance［J］.Applied Intelligence，2000，13（3）：205－213.

［7］TOMLIN C，PAPPAS G，SASTRY S.Conflict resolution for air traffic management：a study in multiagent hybrid systems［J］.IEEE Transactions on Automatic Control，1998，43（4）：509－521.

［8］CHIANG Y J，KLOSOWSKY J，LEE C，et al.Geometric algorithms for conflict detection／resolution in air traffic management［C］∥Proceedings o f the 36th IEEE Conference on Decision and Control.San Diego，CA，1997（2）：1835－1840.

［9］靳学梅.自由飞行空域中多机冲突探测与解脱技术研究［D］.南京：南京航空航天大学，2005.