舰船配电网络拓扑表达新方法

冀欣，张晓锋

（海军工程大学电气工程学院，武汉430033）

0 引言

电力网络的拓扑表达及其分析是配电网管理系统（DMS）的重要组成部分。作为电力系统结构分析与数值计算之间的纽带，电网的拓扑表达对电力系统数字实现的难易程度、可扩充性、可维护性及推理计算效率等方面有直接影响[1]。

舰船配电网络属于辐射状结构，其拓扑表达一般采用邻接矩阵法和支路-节点关联矩阵法，这两类方法能够对节点间或节点与支路间的连接关系进行直观描述[2-5]。对于舰船配电网络，其配电板分散地布置于不同的舱室中。由于各舱室的工作环境不尽相同，因而各配电板的可靠性存在差异[6,7]。为了提高对负载持续供电的能力，需要对各配电板之间的连接关系进行优化。配电网的拓扑结构属于决策变量，它包括配电板间和负载与配电板间的连接关系两部分[8,9]。因此，需要采用适当的电网拓扑表达方法对这两类决策变量进行数学描述。但是，传统的拓扑表达方法不便于计算舰船配电网络的配电层次、配电板的出线数量和各配电板输出功率等配电信息，并且无法保证优化结果满足配电网络的辐射状结构要求。

本文定义了配电板关联矩阵和负载-配电板关联矩阵，分别用于描述配电板间以及负载与配电板间的配电关系，并且针对舰船配电网的辐射状结构建立了相关约束条件的数学模型。对一典型的舰船配电网络结构进行了设计，结果证明了该拓扑表达方法及约束条件数学模型准确性和有效性。

1 舰船配电网拓扑表达方法

舰船配电网络主要由配电板、负载及馈线构成，其拓扑结构是指配电板之间以及配电板与负载之间的连接关系。本文分别定义下列两种矩阵对上述两类连接关系进行数学描述。

1）配电板关联矩阵A。矩阵元素ai,j的取值为0或1。若配电板Sj位于Si的配电下游，即Si向Sj供电，则ai,j= 1；反之则ai,j= 0。另外，矩阵的对角元素取值为1。假设配电网中配电板（含主配电板）的数量为N，则该矩阵为N×N维。

2）负载-配电板关联矩阵B。矩阵元素bi,j的取值为0或1。若负载Lj直接连接于配电板Sj下，则bi,j= 1；反之则bi,j= 0。假设网络 中配电板的数量为N，负载数量为L，则该矩阵为L×N维。

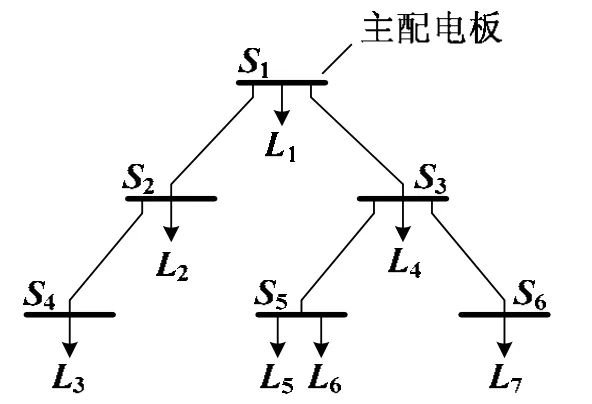
图1 典型舰船配电网络结构示意图

如图1所示，该舰船配电网络中包含6个配电板和7个负载，其对应的配电板关联矩阵A和负载-配电板关联矩阵B分别为

2 约束条件

在舰船配电网络中，各级配电板和馈线构成以主配电板为根节点的辐射状网络。也就是说，对于主配电板外的任意一个配电板，其只能直接连接于一个配电板下[10]。为保证配电板关联矩阵和负载-配电板关联矩阵所描述的配电网络符合辐射状结构性要求，需要建立如下约束条件。

2.1 配电板关联矩阵的约束条件

1）根据定义，除主对角线元素外，矩阵中其余元素取值为0或1。即

其中1≤i,j≤N且i≠j。

2）若配电板Si向配电板Sj供电，则Sj不能向Si供电。该约束可表述为：若ai,j= 1，则aj,i= 0。即

其中，1≤i,j≤N且i≠j。

3）若配电板Si向配电板Sj供电，则位于Sj下游的所有配电板也应位于配电板Si的配电下游。该约束表述为：若ai,j=1且aj,i= 0，则ai,k=1。即

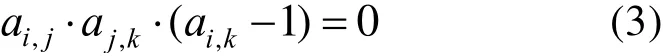
其中，1 ≤i,j,k≤N且i≠j,j≠k,i≠k。

（4）若配电板Si不向配电板Sj供电，且Sj不向Si供电，则由Si供电的所有配电板均不能位于Sj的配电下游。该约束可表述为：若ai,j= 0,aj,i= 0，且ai,k=1，则aj,k= 0。即

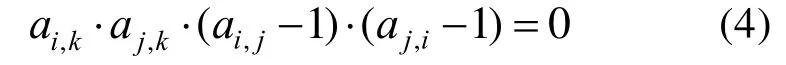
2.2 负载-配电板关联矩阵的约束条件

1）根据定义，矩阵元素取值为0或1。即

其中，1≤i≤L且1≤j≤N。

2）各负载一次仅能连接于一个配电板上。该约束条件可表述为：矩阵B中任意行的各元素中有且仅有一个元素取值为1。即

其中，1≤i≤L。

3 配电网络属性计算

在舰船电网结构分析中，需要计算诸如配电网络的配电层次、各配电板的出线数量和输出功率等诸多配电信息。基于上文定义的配电板关联矩阵和负载-配电板关联矩阵，可以方便地计算出上述配电信息，具体计算方法如下。

1）配电网络的配电层次

配电板关联矩阵A中元素ai,j用于表示配电板Si是否位于Sj的配电下游。假设主配电板的配电层次为第1级，则配电板St的配电层次dt在数值上等于主配电板至配电板St的连通路径上的配电板数量。因此，dt可表示为配电板关联矩阵中第t列的元素之和，即

其中，N为配电网络中配电板的数量。进而，整个配电网的配电层次d可以表示各配电板的配电层次的最大值，即

2）配电板的出线数量

假设配电网络中配电板数量为N，负载数量为L，且配电板Sk和配电板St的配电层次分别为dk和dt，则仅当dk满足

时，式

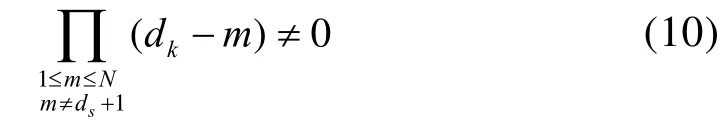
成立。此时，有

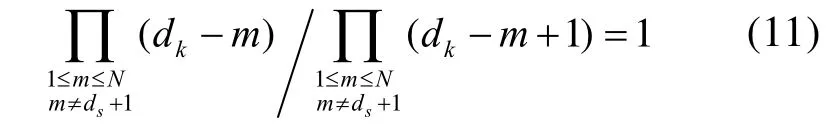
故仅当配电板Sk的配电层次dk满足式（13），且其位于配电板St的配电板下游时，有

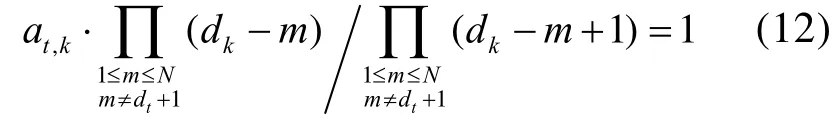
反之，上式等号左边的表达式值为0。因此，仅当式（14）成立时，配电板St直接连接于Sk下。由此，直接连接于配电板St下的配电板数量可表示为

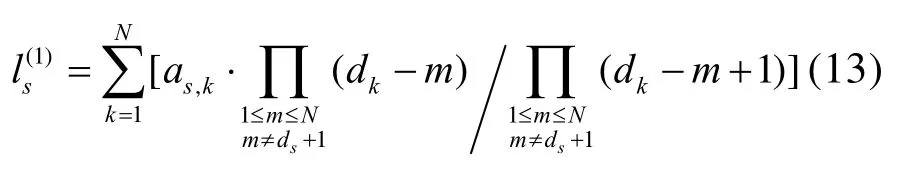
直接连接于配电板St下的负载数量(2)tl可表示为

因此，配电板St的出线数量tl为

3）配电板的总输出功率

假设配电网络中配电板数量为N，负载数量为L。定义N维列向量F、N维列向量F′和L维列向量P。其中，元素fi表示直接连接于配电板Si下负载的总额定功率；元素fj′表示配电板Sj向下游馈送的总功率；元素kp表示号负载kL的额定功率。

根据负载-配电板关联矩阵的定义，直接连接于配电板Si下负载的总额定功率fi可表示为

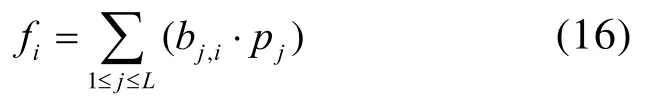
其中，pj为负载Lj的额定功率。直接连接于各配电板下负载的总额定功率的向量F可表示为

其中，向量P表示各负载的额定功率。

根据配电板关联矩阵的定义，配电板Si向下游输出的总功率fi′可表示为

因此，各配电板总输出功率的向量F′可表示为

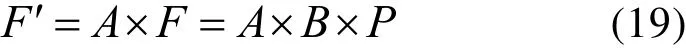
4 算例

基于上文提出的配电网络拓扑描述方法及约束条件数学模型，对一典型舰船配电网络进行优化。该配电网中含有11个配电板和30个负载，如图2所示。各负载的额定功率及其所连接的配电板见表1；各配电板及其对应馈线的独立故障概率见表2。对该配电网络中各配电板间的连接关系进行优化，以保证损失负荷的数学期望值最小。另外，要求该配电网络的配电层次不得超过4级，且各配电板下至多允许连接2个配电板。

该规划问题可表述为：

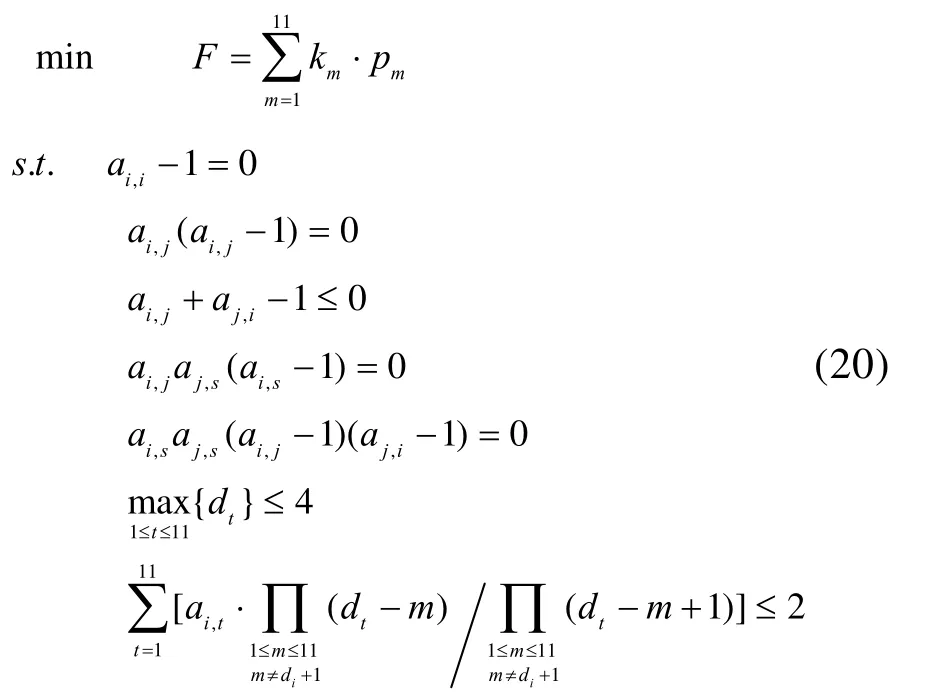
其中，km为配电板Sm的失电概率；pm为直接连接于配电板Sm下的负载总额定功率；且

采用填充函数法求解该规划问题。优化前的配电网损失负荷的数学期望值为2.91 kW；优化后的配电网络结构如图3所示，其损失负荷的数学期望值为2.37 kW，较优化前降低了18.6%，且该配电网络结构满足辐射状结构性要求。

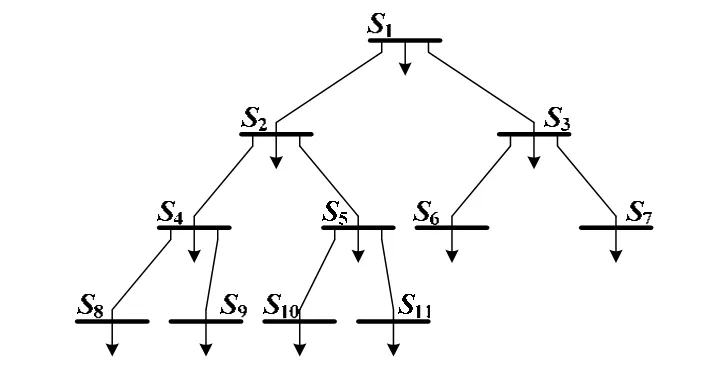
图2 优化前配电网结构示意图

5 结论

本文定义了配电板关联矩阵和负载-配电板关联矩阵，以描述舰船配电网络中各配电板之间以及配电板与负载之间的供配电关系。在此基础上，建立了约束条件以保证这两类矩阵所描述的舰船配电网络满足辐射状结构的要求，并提出了舰船配电网络相关属性的计算方法，为舰船配电网络优化设计提供了前提条件。对一典型舰船配电网络结构进行了优化设计，结果证明了本文所提出的拓扑表达方法的准确性和有效性。

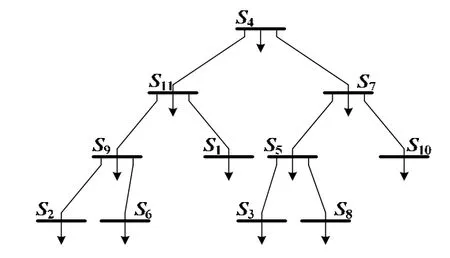
图3 优化后配电网结构示意图

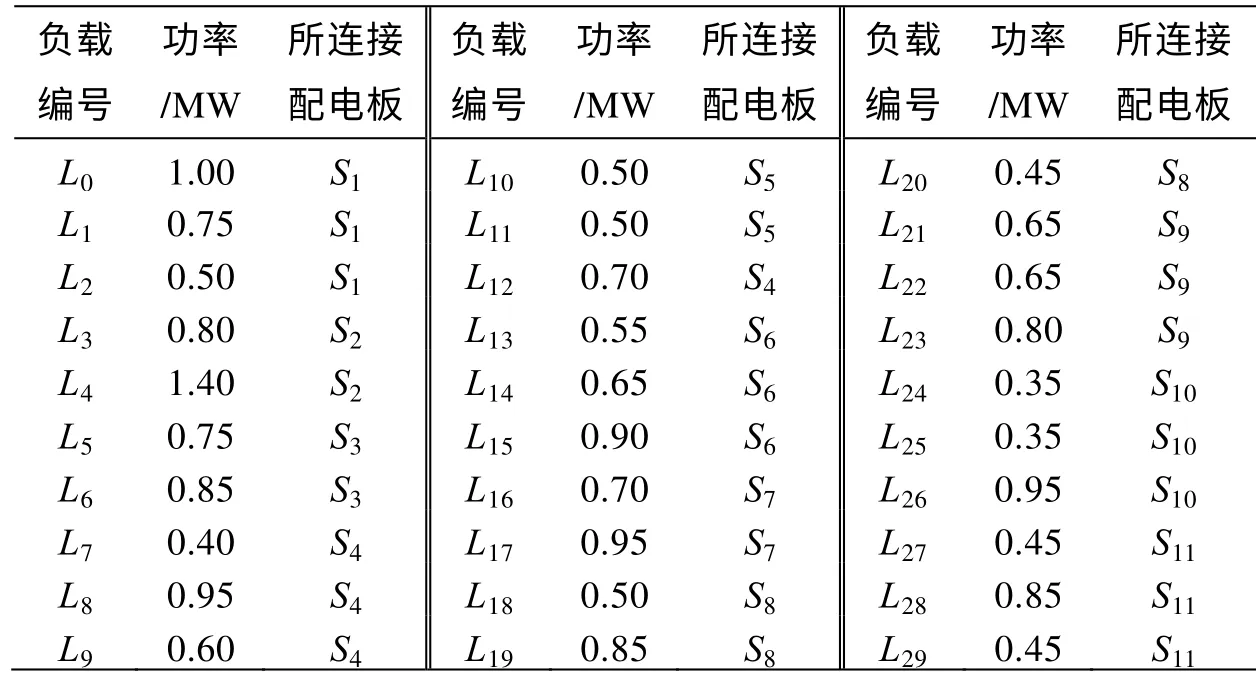
表1 负载参数

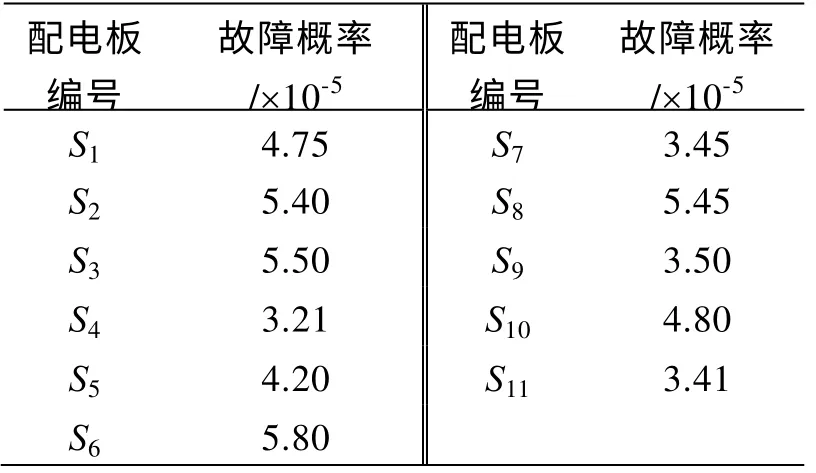
表2 配电板独立故障概率

[1] 黄靖, 张晓锋, 蒋心怡. 一种启发式舰船电力网络拓扑分析方法[J]. 电力系统及其自动化学报, 2008,20(2): 110-116.

[2] 贺宏锟, 史浩山. 基于关联矩阵的网络拓扑辨识方法研究[J]. 西安交通大学学报, 2006, 40(4):477-479.

[3] 程路尧, 庄浩俊, 李哲. 基于邻接矩阵法的独立电网拓扑分析方法研究[J]. 船电技术, 2010, 30(8):19-23.

[4] M Prais, A Rose. A topology processor that tracks network modifications over time[J]. IEEE Trans. on Power Apparatus and Systems, 1988, 3: 992-998.

[5] G A Dgar. Topology and fractal geometry [M]. New York: Springer, 1990.

[6] 孙诗南. 舰船电力系统的研究与设计[M]. 北京: 国防工业出版社, 1990.

[7] 王文义. 船舶电站[M]. 哈尔滨: 哈尔滨工程大学出版社, 2006.

[8] 王锡凡. 电力系统优化规划[M]. 北京: 水利电力出版社, 1990.

[9] 孙洪波. 电力网络规划[M]. 重庆: 重庆大学出版社,1996.

[10] 李麟, 沈兵, 庄劲武. 舰船电力系统[M]. 武汉: 海军工程大学出版社, 2001.