关于正定矩阵的两个定理

卢占化,曹林芬（河南师范大学数学与信息科学学院,河南新乡453007）

关于正定矩阵的两个定理

卢占化,曹林芬
（河南师范大学数学与信息科学学院,河南新乡453007）

引入矩阵反顺序主子式及相关顺序主子式的新概念,并运用反顺序主子式和相关顺序主子式刻画了实对称矩阵的正定性,为研究实矩阵提供了新的思路.同时,给出具体的例子说明了这类矩阵的存在性.

顺序主子式；实对称矩阵；反顺序主子式；相关顺序主子式

实对称矩阵正定性问题是高等代数的重点内容之一[1-3].矩阵的正定性与矩阵的特征值与实二次型、顺序主子式都有密切联系[1,4-5],并且这部分内容对于几何学中相关问题的研究也有极大帮助.众所周知,一实对称矩阵正定的充分必要条件是它的各级顺序主子式大于零[1].这个结论揭示了矩阵正定性与顺序主子式之间的联系.矩阵正定性是实对称矩阵的重要内容之一.本文引入矩阵的反顺序主子式及相关顺序主子式的概念,利用分块阵的初等变换以及归纳方法证明了实对称矩阵A正定的充分必要条件是A的各级反顺序主子式大于零；实对称矩阵A正定充分必要条件是A的各级相关顺序主子式大于零.对进一步研究矩阵,研究二次型及二次型的应用有重要参考意义[6].

1 反顺序主子式

定义1设A为n级方阵

一般地,n级方阵A的反顺序主子式恰为n个.

定理1若A为n级实对称矩阵,则A为正定矩阵的充分且必要的条件为A的各反顺序主子式大于零.

证明：必要性仿照文献[1]易得.

充分性

设A为n级实对称矩阵且满足题中条件

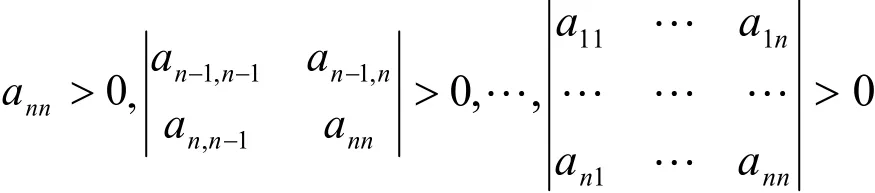
用归纳法证明A为正定矩阵.

首先n=1结论显然成立.假定结论对于n-1级同类矩阵成立,下面分析满足题上条件的n级矩阵A.记

其中A1为n-1级矩阵并且满足题上条件.运用分块阵的初等变换可得

显然B与C合同.

由行列式理论知C＞0,记a-αA-1α′=a,此时a＞0,根据归纳假设正定,因而存在可逆阵G,G′AG =E.

由易知D正定.但是B与D合同,故B为正定阵.

2 相关顺序主子式

定义2设A为n级方阵,如果n为奇数,下列行列式

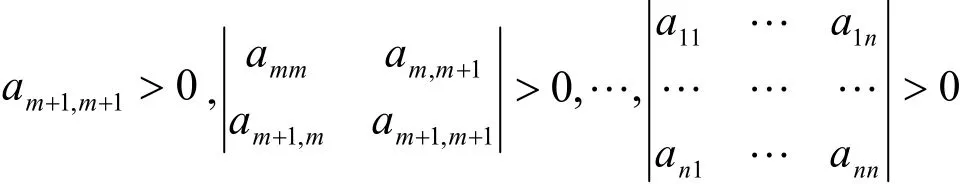
称为元的相关顺序主子式.当n=2m为偶数时,位于m,m+1行,m,m+1列；m-1,m,m+1行,m-1,m,m+1列；…,…；1,2,…,m+1行1,2,…,m+1列；…,…；1,2,…,n行,1,2,…,n列交叉位置上的元按原来的顺序构成的这些行列式称为的相关顺序主子式.

定义3矩阵A施行一次初等行变换,再施行一次同类型的初等列变换,称之为成对的初等变换.

定理2如果A为级n实对称方阵,当为奇数时am+1,m+1＞0,am+1,m+1的相关顺序主子式全大于零,则A为正定矩阵.如果n为偶数,的相关顺序主子式全大于零,则A为正定矩阵.

证明利用成对的初等变换仅对n=2m+1的情况证之.设A满足题上条件

B的各级顺序主子式全大于零,B正定.但A与B合同,因而A正定.当A为偶数阶实对称矩阵时,类似可证A为正定矩阵.

定理证毕.

3 小结

本文结果揭示了反顺序主子式大于零,相关顺序主子式与正定矩阵之间的内在联系.同时也体现出正定二次型中各变量的平行地位,比如以y轴为对称轴抛物线中x与y是对称的.

[1]北京大学数学系几何与代数教研室代数小组.高等代数[M].3版.北京：高等教育出版社,2003.

[2]徐忠,陆全,张凯院,等.高等代数导教、导学、导考[M].西安：西北工业大学出版社,2004.

[3]卢占化.初等变换的若干应用[J].高等数学研究,2006,9（6）：42-43.

[4]樊恽,郑延履.线性代数学习指导[M].北京：科学出版社,2003.

[5]卢占化.秩1矩阵的分解[J].中国科学教育,2005（5）：22-23.

[6]卢占化.迁移在高等代数中的作用[J].高师理科学刊,2006,26（1）：83-85.

（责任编辑：卢奇）

On two theorem s of a positive definitematrix

Lu Zhanhua,Cao Linfen
（CollegeofMathematicsand Information Science,Henan NormalUniversity,Xinxiang453007,China）

Concepts of anti-order principal minor and related-order principal minor was defined.The positive definiteness of a real symmetricmatrix is characterized by using this two concepts,which provides a new way to study realmatrices.Meanwhile,the concrete examples to illustrate the existence of suchmatrix are presented.

symmetricmatrices；anti-order principalminor；related order principalminor；principalminor

G442

A

1008-7516（2013）02-0057-03

10.3969/j.issn.1008-7516.2013.02.014

2013-01-29

国家自然科学基金（11001076）；河南省教育厅项目（2011A110008）

卢占化（1955-）,男,河南洛阳人,硕士,副教授.主要从事代数学研究.

曹林芬（1975-）,女,河南林州人,博士,副教授.主要从事几何与代数研究.