决策表方程描述及在作物病害诊断中的应用

罗来鹏

（华东交通大学基础科学学院,江西南昌330013）

决策表方程描述及在作物病害诊断中的应用

罗来鹏

（华东交通大学基础科学学院,江西南昌330013）

以粗糙集中属性约简的核属性求解与应用问题,为决策表提出一种基于矩阵方程的描述方法.首先将各属性所决定的等价类用矩阵来表示,然后建立一个以矩阵为系数的矩阵方程并转化为一般方程组,根据属性约简以及核属性的定义,通过求解该方程组某个方程的最优解,得到对应的核属性.给出了该方法一般步骤,并将该方法应用到一个棉花疾病诊断系统中,验证其有效性.

粗糙集；数据挖掘；属性约简；疾病诊断

粗糙集是1982年由波兰学者Pawlak提出的一种处理不确定性的数学理论[1].它主要用来处理一个概念在一组标准基（等价类）下的近似表示与计算.当一个概念不能完全由给定的标准基来表示时,由此导出一对上、下近似集[1-2].粗糙集在处理数据方面一个重要特征是不用象模糊集那样需要先验知识隶属度,处理结果更能反映问题客观本质.近年来粗糙集在数据挖掘、机器学习、农业领域等方面得到广泛应用[3-6].它应用的主要理论基础是在满足条件属性与决策属性所决定的等价类之间关系的条件下,对于用表来表示的信息系统进行属性约简来获取更为简洁的规则知识.但是实际应用中,由于信息系统中的关系、论域、对象、概念的复杂性、多样性和不确定性,传统的粗糙集模型很难满足应用需求.近些年来建立与发展了多种类型的粗糙集模型,如：变精度粗糙集模型、模糊模型、随机模型等,在这些模型下得到代数方法、信息熵的约简方法、区分矩阵方法等很多不同的约简方法.这些模型与方法能很好地解决不同条件下的粗糙集理论与应用问题,也极大丰富了这门新兴不确定性的处理理论.矩阵是信息处理中一种重要的计算工具,由于它直观、计算简便、易于在计算机上实现,得到了广泛应用.利用矩阵来研究粗糙集也有不少结果.Guan JW等[7]最早提出了信息系统下的矩阵算法,将信息系统下的等价关系用矩阵的形式进行了重新描述,并基于此提出了新的约简算法.国内在此方面也进行了一些研究,发展了该方法的一些计算,并将该方法推广到更为一般的决策表矩阵计算与属性约简[8-10].本文结合这些结果对决策表提出一种新的描述方法,将决策表描述为矩阵方程形式,通过对矩阵方程的求解与计算,获取其核属性,并将方法应用到一个作物疾病的诊断系统中.

1 基本概念

定义1：一个知识表示系统S是一个四元组,可表示为S=（U,R,V,F）.其中U是有限对象的集合, R=C∪D是有限个属性的非空集合,V是属性值的集合,F为信息函数F：U×R→V.当子集C和D分别为条件属性和决策属性时,知识表达系统又称为决策表[1].

对于任何条件,都可以决定一个等价关系,所有等价类集合表示为U/B,设U/B={X1,X2,…Xm},其中Xi∩Xj=Φ,i≠j.i,j=1…m并且

在决策表中,如果一个条件属性的删除不改变条件属性和决策属性集合所决定的等价类之间的关系,那么该属性是可删除或者说不重要的,一个决策系统的属性约简总是存在但往往不是唯一的.

设{Bi,i≤k}表示系统的所有约简,则为系统的核心.一般来说,核心属性不一定构成约简,若核心集非空,则任何约简都包含核心属性,且核心中的属性是任何约简都必须的,因而是绝对必要属性.是相对必要属性,出现在某些约简中.是绝对不必要属性集,不出现在任何约简中.

对于协调决策表,如果记Dd（[xi]C,[xj]C）为[xi]C与[xj]C的决策辨识集,则下列命题等价[3]：

（1）a∈C为核心属性；

（2）存在xi,xj∈U,Dd（[xi]C,[xj]C）={a}；

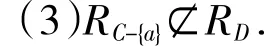
定义2：设B是域U上的等价关系,则B对应一个方阵为：MB=[pij]n×n,其中n=.否则矩阵MB称为B的关系矩阵或者B的属性矩阵[7].

这样的矩阵主对角线上元素都为1,且具有对称性与稀疏性（就是有很多0元素）的特点.同一行中等于1的为相同的类.这种表示是一一对应的,并且之间一些计算可以转化为矩阵的形式.

定义3：设矩阵M=[mij]n×n,W=[wij]n×n,对于任意i,j（i,j≤n）,若有mij≤wij,则记为：M≤W；若有mij≥wij,则记为：M≥W.

根据定义3,决策表S=（U,C∪D）中,如果有条件属性集关系矩阵与决策属性集关系矩阵MC≤MD,那么该决策表是协调的,否则不协调.同时也很容易得到在协调决策表中,若属性集为一个约简,当且仅当满足：①MA≤MD；②不存在且MA′≤MD.

显然可利用上述方法来判断一个属性是否重要,但是由于矩阵中的元素为0或1,所以判断某个属性是否重要可以进一步简化为只需要比较MD是否等于0则可.同时也容易得到更进一步的求解核心属性的方法.

若记[Ma]ij为属性a所决定的关系矩阵第i行第j列的元素,则下列命题也等价：

（1）a∈C为核心属性；

（2）存在i,j有[Ma]ij=1,而任何b∈C,[Mb]ij=0；

（3）RC-{a}≤RD不成立.

2 决策表矩阵方程的描述

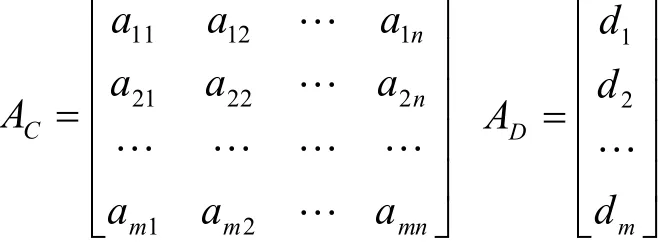
在数据挖掘与智能信息中,常用矩阵或向量来表示对象的基本特征或对象之间的某种关系,如：用p个属性来描述n个对象,在数据库中可以用一二维表来描述,也可用数据矩阵来描述.数据矩阵是一个对象-属性结构,通常也称为双模式矩阵,结果如下

每一行描述一个对象,每一列表示不同对象在相同属性上的取值.也就是说可以借助数据矩阵对应表示一张关系二维表.决策表S=（U,C∪D）见表1,条件属性集C={C1C2…Cn},D为决策属性.

表1 一般决策表Tab.1 Generaldecision table

若记

根据属性约简定义,一个属性集为约简集,必须要满足：①不能改变原来表中所蕴涵的条件属性与决策属性集之间的关系；②所含属性是某次迭代计算过程中属性个数最少的.从方程解的角度来说,方程的解为最优,一方面必须满足关系式；另外一方面非零解X应该是最优解.在所有最优解中如果xi=1,那么Ci一定为核属性.

由于关系很难转化为一种数学的计算,为此将结果作进一步处理.根据定义2,每一个属性都可以决定一个等价关系,而等价关系可以用一个关系矩阵来表示.因此如果记MCi表示Ci所决定的关系矩阵,那么方程可以表示为（其中⊕表示的是一种运算,具体看实际情况）.

如果决策表是协调的,那么式子可变为：满足①MC1⊕表示一种取小运算）条件下,求X.

需要说明的是,如果xi=0,那么Mc·ixi予以删除,不参与任何运算.

3 方程的解与核属性计算

由于各关系矩阵中有很多0元,具有很大的稀疏性,因此得到很多重复与无效的方程,真正有效方程个数不多.虽然求解简化后方程组的所有最优解有一定的困难,但是在实际中求解一些特殊的解（比如核属性所对应的解）来判断核属性是完全可行性的.核属性在任何约简中都必须存在,联系方程组,在所有的最优解中核属性所对应的分量必须都是1.如果方程组中,存在某个方程的最优解是唯一的而且只有一个非0分量,那么非0分量所对应的属性必为核属性.如果有多个这样方程,那么所有的这样属性集为核心属性集.归纳起来具体步骤如下：

步骤1：计算条件各属性及决策属性集的关系矩阵；

步骤2：构造矩阵方程,列出方程组；

步骤3：找唯一0方程,对应属性为核心属性,所有核心属性构成的集合为该系统的核心属性集.

4 应用算例

表2为一棉花病害的诊断系统,其中{a,b,c,d}为条件属性集,e为决策属性.分别表示为：a-“diseased spotcolor”,b-“disease site”,c-“disease shape”,d-“feature”,e-“the type ofdisease”,计算导致该病害的核心因素.

表2 棉花病害诊断算例Tab.2 An exampleofcotton desease diagnosis

（1）计算各属性的关系矩阵

（2）构造矩阵方程

（3）转化为有效方程组（删除了重复和结论显然成立的）

分析这个方程组的解答情况：若方程（1）成立,那么x1必须为1；若方程（2）成立,只需x1或x2或x4为1即可；若方程（3）成立,只需x2或x4为1即可；若方程（4）成立,只需x2或x3为1即可；若方程（5）成立,只需x1或x3或x4为1即可.从方程（1）来看,属性a必须要存在,是不可缺的,所以属性a必为核属性.在整个方程组中这种形式的方程是唯一的,最优解只有一个,因此核属性集合为a,结果与其地方法相同.也就是因素a-“diseased spotcolor”是致病的关键因素.

5 结论

属性约简是粗糙集应用中的核心内容,核心属性计算与求解体现核心关键指标,先约简再求核心属性非常复杂.虽然研究人员一直在寻求高效的属性约简算法,并取得了一定成果,但更多的集中在代数方法、信息熵、分辨矩阵、布尔矩阵等方面.本文所提出的矩阵方程方法不仅直观,而且计算简单,对于使用粗糙集来分析指标因素的重要性具有一定价值.

[1]Pawlak Z.Rough sets[J].International JoumalofParallelProgramming,l982,11（5）：34l-356.

[2]张文修,梁怡,吴伟志.信息系统与知识发现[M].北京：科学出版社,2003.

[3]李树平,赵杰,夏春艳,等.粗集理论在农业生产中的应用[J].安徽农业科学,2011,39（29）：17762-17763.

[4]朱琼瑶,张光新,冯天恒,等.基于粗糙集和证据理论的水质分析预警技术研究[J].浙江大学学报：农业与生命科学版, 2012,38（6）：747-754.

[5]吴昊,李书.基于粗糙集的属性约简算法在农业机械中的应用[J].农机化研究,2009（3）：171-174.

[6]徐月,徐艳蕾,黄东.基于粗糙集的迭代阈值选择的玉米苗期背景分割算法研究[J].吉林农业大学学报,2012,34（4）：459-463,467.

[7]Guan JW,BellDA,Guan Z.Matrix computation for information systems[J].Information Sciences,2001,131（1/4）：129-156.

[8]罗来鹏,刘二根,曾毅.粗糙集理论研究的矩阵方法[J].系统工程与电子技术,2009,31（4）：859-862.

[9]王磊,李天瑞.基于矩阵的粗糙集上下近似的计算方法[J].模式识别与人工智能,2011,24（6）：756-762.

[10]XuW H,LiY,Liao XW.Approaches to attribute reductions based on rough setandmatrix computation in inconsistentordered information systems[J].Knowledge-Based Systems,2012,27（3）：78-91.

（责任编辑：卢奇）

Equation description of decision table and its application in desease diagnosis of crop

Luo Laipeng
（SchoolofBasic Sciences,EastChina Jiaotong University,Nanchang330013,China）

Aiming at the computation and application problem of core attribute in rough set,a description method of decision table based on matrix equation is presented.Firstly,equivalence classes introduced from all the attributes are expressed by matrix,matrix equation whose coefficient is above matrix is built.Matrix equation is transformed to general equations.According to definition of attribute reduction and core attribute,the optimal solution of equation is correspondence core attribute are obtained.At last,the general steps and effectiveness of the approach are shown in an desease diagnosis of cotton.

rough set；datamining；attribute reduction；desease diagnosis

TP182

A

1008-7516（2013）04-0048-05

10.3969/j.issn.1008-7516.2013.04.012

2013-05-11

华东交通大学校立课题（10JC04）

罗来鹏（1973-）,男,江西吉水人,硕士,副教授.主要从事粗糙集理论与应用研究.