基于D-S证据理论直接求代数约简和代数核*
2011-07-24曾凡智卢炎生黄国顺
曾凡智,卢炎生,黄国顺,文 翰
(1.佛山科学技术学院 计算机系,广东 佛山 528000;2.华中科技大学 计算机学院,湖北 武汉 430074;3. 佛山科学技术学院 理学院 ,广东 佛山 528000)
粗糙集(Rough Set)理论是由波兰数学家Pawlak[1]于20世纪80年代初提出的用于数据分析的理论,作为处理不确定信息的有效工具,粗糙集理论已被成功地应用于数据挖掘、机器学习与知识发现、模式识别等领域,成为当前研究热点之一。
属性约简是Rough 集理论的核心问题之一,也是知识获取的关键步骤之一,因此属性约简研究深受各研究者的关注。目前已有多种属性约简方法被提出,归纳起来主要有Pawlak原始定义的属性约简,称之为代数约简; 基于条件信息熵的属性约简(称之为信息熵约简)[2-3];基于包含度理论的分布约简、最大分布约简、分配约简及近似约简等[4];基于D-S证据理论的属性约简方法等[5-7]。其中信息熵约简与分布约简是完全等价的[8],分配约简与近似约简也完全等价。对于一致决策表,上述各约简方法所得约简结果是一致的,但在不一致决策表下,它们所得的各约简结果及核属性都不尽相同[9-12]。针对不一致决策表,目前通常的处理过程是将不一致决策表转化为一致决策表,再对所得到的一致决策表计算其代数约简[6-9],其中文献[6]的方法先将不一致决策表转化为一致决策表,然后基于D-S证据理论求出其广义决策约简,然而具体的算例表明广义决策约简与原始决策表的代数约简并不相同。本文的研究结果表明广义决策约简仅与分配约简等价。与广义决策约简为了维持某种“不变”的判定指标而人为去将不一致决策表转化成一致决策表不同,本文修改了求属性约简的判定指标,从而避免将不一致决策表转化为一致决策表这一过程,提出一种不需转换过程,直接针对不一致决策求出其代数约简和代数核的新方法。
1 相关基本概念
定义1 决策表S=
若POSC(D)=U称其为一致决策表,如果POSC(D)=∅称其为完全不一致决策表,其余情形称为部分不一致决策表。若POSB(D)=POSC(D), 则称B为C的代数协调集,若B是C的代数协调集且B的任何真子集都不是其代数协调集,则称B为C相对于D的代数约简。
由于判断两集合是否相等比较费时,文献[13]提出一种简化的判断方法,即POSC(D)=POSB(D)的充分必要条件是|POSC(D)|=|POSB(D)|, 它将判断一个属性集B是否为条件属性集C的代数协调集简化为只需判断两集合的基数是否相等,从而大大简化了计算过程,提高了计算效率。
定义2 给定决策表S=
文献[10]指出,当时B⊆C,对任意的x∈U,δB(x)=δC(x)当且仅当∀y∈[x]B,δB(y)=δC(x)。 这为分布约简的判断提供了途径。
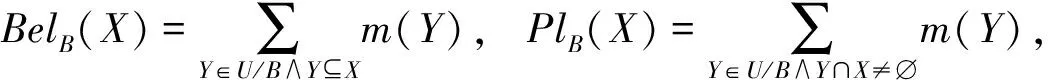
定理1[6]若S=
1)RBRD;

对于不一致决策表S=
定理2[6]设S=
1)B⊆C是C的广义决策约简;
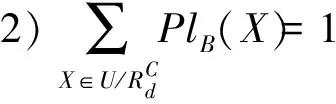

2 广义决策约简等价于分配约简
本节将首先通过具体的算例说明,在不一致决策表下,广义决策约简与代数约简并不完全一致,然后从理论上证明广义决策约简实质上只与分配约简等价。
先考察文献[14]的算例。
例1 在表1的决策表S1中,U={x1,x2,…,x6},C={a,b,c},D={d}。

表1 决策表S1
易得POSC(D)={x6},其代数约简为{b}。如果按照求广义决策约简的计算方法,其广义决策值∂C(x)如表2 所示。

表2 决策表S1的∂C(x)

虽然广义决策约简与代数约简在不一致决策表上所得的结果并不完全相同,下面结论指出广义决策约简和分配约简是等价的。
定理3 给定决策表S=
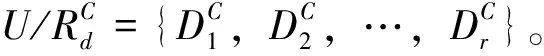
反之,若RB则对∀x∈U,有某个存在,使得[x]B⊆又因决策表

1)RB
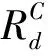
根据定理3和4知,B⊆C是C的广义决策协调集当且仅当它是C的分配协调集,从而知道广义决策约简与分配约简是等价的。根据文献[12]知,广义协调集必为代数协调集,从而知,若存在一个代数约简,则一定存在一个相应的广义决策约简,使得该代数约简是相应广义决策约简的子集,但两者并不完全一致,如例1中的决策表S1,其代数约简为{b}, 广义决策约简为{a,b},{b}⊆{a,b}。
3 基于D-S证据理论直接求代数约简和代数核的方法
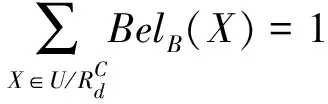
基于以上事实,下面提出一种求属性约简新的判定指标,从而跳过将不一致决策表转化为一致决策表这一过程,提高了计算效率。理论上证明了其计算过程一定能得到代数协调集和代数核。
属性约简新的判定指标由下面的定理给出。
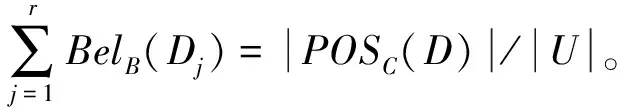

上述证明过程是可逆的,从而有结论成立。

证明根据代数协调集与代数约简的定义及定理5知结论成立。

若决策表S的相对核为CORE(C,D), 由此给出基于D-S证据理论的代数核属性判断准则推论2。

证明根据定理5和相对核CORE(C,D)的定义即知结论成立。
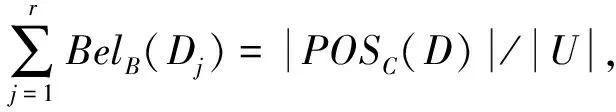
4 计算实例
通过两个算例说明采用新的属性约简的指标函数,直接求代数约简与代数核新方法的有效性。
例2 继续考察例1决策表S1。
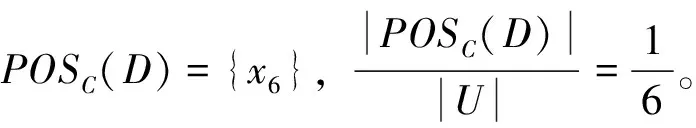
为进一步说明广义决策约简、分配约简与代数约简之间的异同以及本文求代数约简和代数核的新方法,引用文献[10]的算例进一步验证如下。
例3 给定决策表S2=

表3 决策表S2


表4 U/C等价类的分配函数值与广义决策值

显然δB(x)=δC(x),∂B(x)=∂C(x),同理,若令B={a,c,e,g},知其也是广义决策协调集.并且可验证它们都是C的分配约简和广义决策约简。

表5 U/B等价类的分配函数值与广义决策值


5 结 语
基于D-S证据理论的属性约简方法在一致决策表上所的结果与代数约简的结果是一致的,对于不一致决策表,现有的方法是先将不一致决策表转化成一致决策表,然后求其广义决策表约简,但它与代数约简并不完全相一致.本文讨论了这种不一致性问题,理论上证明了广义决策约简仅与分配约简等价,进一步地,提出了一种在D-S证据理论下采用新的属性约简指标直接求代数约简和代数核的新方法,从而避免了不一致决策表转化的问题,减少了转换的复杂度与提了算法效率,为在不一致决策表下直接计算代数约简的高效算法的探索打下了基础。
参考文献:
[1]PAWLAK Z. Rough sets [J]. International Journal of Information and Computer Science,1982,11(5):341-356.
[2]MIAO Duoqian,WANG Ju. An information represention of the concept and operations in rough set theory [J]. Journal of Software,1999,10(2):113-116.
[3]王国胤,于 洪,杨大春. 基于条件信息熵的决策表约简[J].计算机学报,2002,25(7):759-766.
[4]ZHANG Wenxiu,MI Jusheng,WU Weizhi. Approaches to knowledge reductions in inconsistent systems [J]. International Journal of Intelligent Systems,2003,18(4): 989-1000.
[5]ZHANG Mei,XU Lida,ZHANG Wenxiu,et al. A rough set approach to knowledge reduction based on inclusion degree and evidence reasoning theory [J]. Expert Systems,2003,20(5): 298-304.
[6]WU Weizhi,ZHANG Mei,LI Huaizu et al. Knowledge reduction in random information systems via Dempster-Shafer theory of evidence [J]. Information Sciences,2005,174: 143-164.
[7]曾凡智,卢炎生.不一致决策表下基于D-S证据理论的知识约简[J] . 小型微型计算机系统,2009,30(2): 317-321.
[8]袁修久,张文修.决策表的分布约简和严凸函数下约简的等价性[J].系统工程,2003,21(5): 5-7.
[9]WANG Guoyin,ZHAO Jun,AN Jiujiang et.al.. A comparative study of algebra viewpoint and information viewpoint in attribute reduction [J]. Fundamenta Informaticae,2005,68(6):289-301.
[10]李凡,刘启和,叶茂,等. 不一致决策表的知识约简方法研究[J]. 控制与决策,2006,21(8): 857-862.
[11]黄国顺,刘云生. 不一致决策表信息熵约简与代数约简的核计算与转化[J].小型微型计算机系统,2008,29(2):308-312.
[12]黄国顺,刘云生. 不一致决策表各种属性约简的不一致性分析与转化[J]. 小型微型计算机系统,2008,29(4): 703-708.
[13]黄国顺. 基于数据库系统的决策表核和属性约简算法[J]. 计算机应用,2008,28(5):1180-1182.
[14]王国胤. 决策表核属性的计算方法[J]. 计算机学报,2003,26(5):611-615.
