含分布式电源的配网无功优化混合算法

王卫平，王主丁，张 昀，王 凯，申 威，赵俊光

（1．输配电装备及系统安全与新技术国家重点实验室，重庆大学电气工程学院，重庆 400044；2．杭州市电力设计院有限公司，杭州 310009；3.杭州市电力局，杭州 310009；4.重庆市电力公司江津供电局，重庆 402260）

含分布式电源的配网无功优化混合算法

王卫平1，王主丁1，张 昀2，王 凯3，申 威3，赵俊光4

（1．输配电装备及系统安全与新技术国家重点实验室，重庆大学电气工程学院，重庆 400044；2．杭州市电力设计院有限公司，杭州 310009；3.杭州市电力局，杭州 310009；4.重庆市电力公司江津供电局，重庆 402260）

针对多机电为了保证分布式电源并网后配电网的电压控制在一个合理的水平，同时解决以设备安装容量作为无功上/下限约束可能造成解搜索空间偏大的问题，文中提出一种基于节点补偿容量动态区间法的含分布式电源的配电网无功电压运行优化混合算法。在种群进化后期，引入模拟退火法、罚因子自适应调整机制及动态灾变算法，以改善算法寻优质量及精度。通过算例分析验证了本文算法的高效性及实用性。

配电网；无功电压运行优化；分布式电源；节点补偿容量动态区间法；改进遗传混合算法

配电网无功电压运行优化是电力系统提高电压合格率、降低损耗的一个重要途径，因而受到了广泛的重视[1-5]。传统的电力系统无功优化控制策略可归纳为两类[6]：一类属于局部优化控制方法，如变电站的电压无功控制VQC（voltage quality control）；另一类属于全局优化方法，如自动电压控制AVC（automatic voltage control），着重于从全局的角度实现无功/电压的自动优化控制，达到电压优质和网损最小。另外，根据问题研究的时间长短，无功运行优化研究有静态和动态无功优化两类。静态无功优化一般只针对电力系统某一时间断面的运行方式进行的无功优化，以有功损耗最小为目标，并考虑电压等约束。动态无功优化一般在数学模型中引入一天内设备动作次数的约束，以获得整天电能损失最小的全天各时段无功调度模式。

鉴于无功电压优化模型的混合非线性特性，求解方法主要有数学规划法和各种智能方法。文献[8]将遗传算法和Alopex方法相结合作为无功优化的求解方法，可实现全局优化，又具有一定方向性。但算法在初始解生成中，以设备安装容量作为无功上限约束，对于在轻载负荷情况时，可能导致搜索解空间偏大。文献[9]提出一种改进遗传混合算法，其运用于无功规划优化之中，取得较好效果，但该文只考虑了补偿容量上限约束，而未能给出补偿动态区间约束，也没有考虑到有载调压变压器分接头和分布式电源的影响。

分布式电源DG（distributed generation）的接入为电网运行优化提供了新的调节手段。将DG与传统无功电压调整装置相协调配合，以达到对电网实时、经济、可靠地控制，成为当前研究的热点[10-12]。文献 [10]将能够提供无功功率的分布式电源与传统的电压调节手段相结合，建立了无功优化问题的多智能体免疫模型，利用基于聚类和竞争克隆机制的多智能体免疫算法实现无功优化。文献[11]提出基于遗传算法的含分布式电源的配电网无功优化算法，构建包含分布式发电系统的配电网无功优化数学模型，考虑了网损最小和节点电压约束。文献[12]引入静止无功补偿器SVC（static var compensator）作为配电网补偿设备并考虑配电网中可控制无功输出的柴油发电机的无功贡献，建立以有功能耗费用、SVC安装费用和柴油发电机无功生产费用为目标函数的含风力发电的配电网无功优化模型。

静态无功优化是动态无功优化的基础，而且已有不少文献可将动态无功优化转化为静态无功优化[6～8]，因此本文重点分析和研究含DG的配电网静态无功优化，提出一种基于节点补偿容量动态区间的无功电压运行优化混合算法。通过变电站主变分接头、DG和无功补偿装置（包含变电站低压母线侧、中压馈线及配变低压侧补偿）的协调控制，实现中低压配电网的全局优化运行。如果在变电站主变分接头及变电站低压母线电容器组的调度权属上级电网AVC的情况下，可将上级电网AVC系统优化得到的变电站低压母线电压作为已知值，仅对DG、中压馈线及配变低压侧并联电容器组进行协调控制，实现馈线的无功优化。

1 含分布式电源的配电网无功优化模型

本文建立综合考虑DG、有载调压变压器分接头及并联电容器组协调控制问题的无功优化模型，实现在满足技术条件下系统的有功降损效果最大。

1.1 目标函数

本文目标函数为

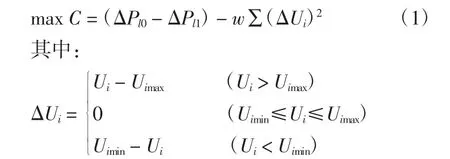
式中：ΔPl0为系统无功优化前的最大有功功率损耗，kW；ΔPl1为系统无功优化后的最大有功功率损耗，kW；Ui、ΔUi为节点i的电压、电压越界值；Uimax、Uimin为节点 i电压的允许上下限；w为惩罚因子。

1.2 约束条件

无功优化的等式约束为功率平衡方程

式中：PGi、QGi分别为节点i的发电机有功功率、无功功率；PDi、QDi分别为节点i的负荷有功功率、无功功率；Ui、Uj为节点i、j的电压幅值；Gij、Bij为节点i、j之间的电导、电纳；δij为节点i、j之间的电压相角差；j∈i表示所有与节点i相连的节点。

控制变量（即变压器的分接头档位、无功补偿装置的投切组数和分布式电源的无功出力等）的约束条件为

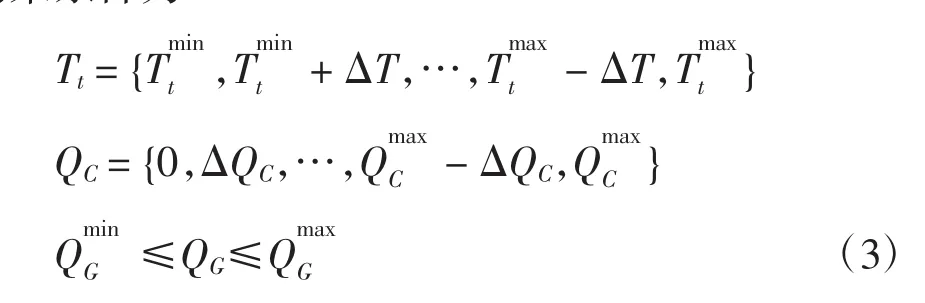
式中：变压器分接头Tt和无功电容器QC为离散变量，其中分别为变压器的总档位数和无功电容器的总补偿组数；分布式电源无功出力QG为连续变量，分别为无功出力上、下限值。分布式电源能否向电网提供无功补偿取决于分布式电源的并网形式[10]。变速恒频双馈风电机组能够按系统调度在其容量范围内发出或吸收无功。燃料电池、光伏系统和微透平机组等DG通过控制并网逆变器，向电网提供无功。柴油机、小水电和海洋能等基于励磁电压可调型同步发电机的DG通过同步发电机励磁系统，调节其无功输出。

状态变量的不等式约束条件为

2 含分布式电源配网节点无功补偿动态区间计算方法

在配电网运行优化研究中，电容器组、分布式电源的位置及相应的可调无功容量的范围约束已给定。但此约束可能只适合最大负荷情形，同时考虑到节点在无功补偿后对无功分布的影响，因此若将设备的极限调节容量作为遗传算法中随机产生初始解的上限/下限约束值，则相当于扩大了算法搜索空间，难免会产生一定数量的不可行解而影响求解效率。为此，本文提出了节点无功补偿动态区间的计算方法。通过定量计算基于补偿降损效果最大、基于节点电压约束两种情况下的节点无功补偿上/下限，构建节点无功补偿动态区间（综合构建方法详见本文3.2节步骤3）。在满足节点电压要求和配网经济运行条件下，该区间将随着其它节点无功补偿及主变分接头档位的随机调节而实现双向动态变化，有效压缩算法搜索空间。

2.1 基于补偿降损效果最大的补偿容量上限/下限

假定单独在节点i进行无功补偿时，所带来的降损效益Ai可近似表示为

式中：H为节点i的所有上游支路（指从源节点出发到达该节点的最短路径上的所有支路）的集合；Qb为补偿节点上游支路最新（动态）最大无功潮流；Qic为节点i的无功补偿容量，由电容器装置或分布式电源提供，当为分布式电源时，其值可正亦可负；Rb为支路b的电阻；Ub为支路b下游端节点的电压。

将Ai对Qic求导，得

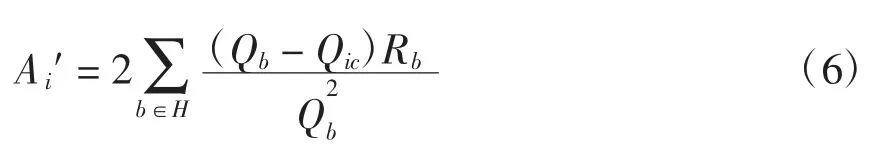
令Ai′=0，本次单独（考虑了其他优先补偿节点已确定的无功出力）在节点i最佳补偿时的无功功率，并将其设置为上限值

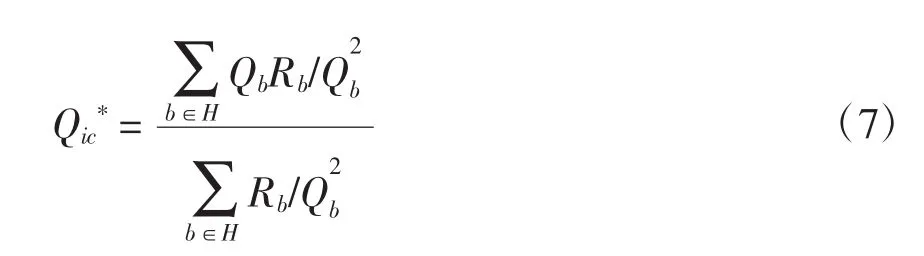
2.2 基于节点电压约束的补偿容量上限/下限

当单独在节点i补偿无功容量为Qic时，节点的电压可近似表示为

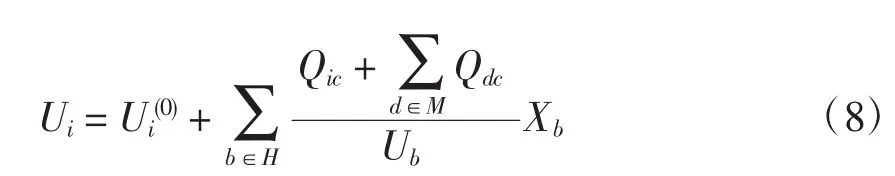
式中：Ui(0)为节点i无功补偿前的电压；M为节点i所有下游支路的集合；Qdc为支路d下游端节点补偿的无功容量；Xb为支路b的电抗；Ub为支路b下游端节点电压。

当考虑变压器分接头对各节点电压的影响时，式（8）可进一步表达为

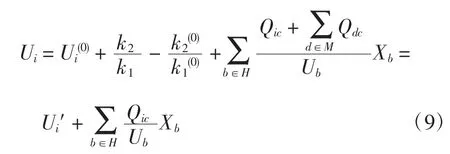
式中：k1=U1/U1B；k2=U2/U2B（上标“0”表示节点i无功Qic补偿前的值）；U1、U2分别为高压变电站主变一次侧和二次侧绕组实际匝数相对应的电压；U1B、U2B分别为主变一次侧和二次侧相连网络的基准电压；Ui′为Qic=0时节点i无功补偿前的电压。

根据计算得到的节点i无功补偿前的电压Ui′，分别对Ui′高于规定上限值、Ui′低于规定下限值和Ui′合格等3种不同情况进行节点无功补偿容量上限或下限的计算。

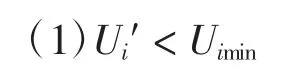
配电网中，各节点的电压值不能低于规定的下限值Uimin，即

把式（9）带入式（10）可得到考虑变压器分接头对节点电压的影响时，节点i满足电压要求所需的最小补偿容量

（2）Ui′＞Uimax

配电网中，各节点的电压值不能高于规定的上限值Uimax，即

把式（9）带入式（12）可得到考虑变压器分接头对节点电压的影响时，节点i满足电压要求所需的最大补偿容量

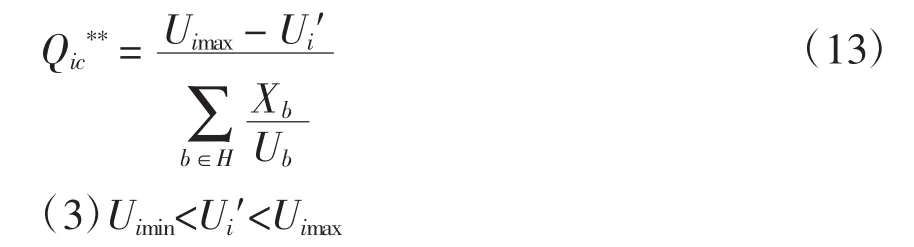
节点i的电压满足要求，有

3 配电网无功电压综合协调优化算法

3.1 编码

在本文算法中染色体采用实数与整数混合编码的方式，基因信息包括变压器主变分接头档位、无功补偿点的电容器补偿组数和分布式电源的无功出力。其中，变压器的变比和补偿电容器组数属于离散变量，分布式电源的无功出力属于连续变量。结合前面的数学模型，文中的染色体编码X为

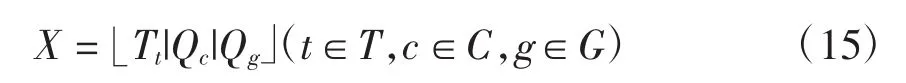
式中：T为有载调压变压器集合；C为无功电容器的补偿点位置集合；G为分布式电源的补偿点位置集合。

3.2 初始种群的动态生成策略

本文提出的初始种群的生成方法具体步骤如下。

步骤1对属于集合T内的主变分接头，分别在其档位调节约束范围内随机产生一数值，作为当前初始解中主变的变比参数。

步骤2基于节点优化编号[13]顺序对节点k进行补偿，k∈（C∪G）。

步骤3确定节点k的动态最大/最小计算补偿容量Qkc，m。其大小应与其上游支路的最新动态无功潮流（详见步骤7）和相应主变分接头档位最新的位置相关。

（1）如果分别由式（7）和式（11）计算得到该节点的Qkc*和Qkc**，则取两者值较大者作为Qkc，m值；

（2）如果分别由式（7）和式（13）计算得到该节点的Qkc*和Qkc**，则取两者值较小者作为Qkc，m值；

（3）如果分别由式（7）和式（14）计算得到该节点的Qkc*和Qkc**，则取Qkc*作为Qkc，m值。

步骤4检查Qkc，m是否超出节点设备容量上下限的约束：

步骤5若补偿节点时k∈C，补偿的电容器组数上限mkc，max可表示为

式中，Qkc为电容器标准容量。由于电容器无功补偿是以组为单位，是离散的整数，而mkc，max可能计算出来不是整数，本文保守的取其上限整数值（非负，最小值为0）。

在[0，mkc，max]之间产生一个随机的整数，它即为在这一个解中此节点补偿的标准电容器组数，用这个整数乘以电容器的单位容量可得此节点无功补偿的近似容量。

步骤6若补偿节点k∈G时，Qkc，m属于连续型变量。在[0，Qkc，m]之间产生一个随机的实数值，以作为该节点分布式电源的无功出力。

步骤7使用节点优化编号中得到的上游节点信息可找到此节点上游的所有支路，将这些支路潮流的无功功率分别减去此节点的无功补偿的容量，所得的结果为相应支路更新后的无功功率。

步骤8如果节点k是（C∪G）集合中最后一个节点，则转到步骤9；否则，转到步骤2（按次序对下一个补偿点进行补偿）。

步骤9停止。

至此，一个初始解已生成，重复如此操作便形成了初始种群中的各解。

以上过程既具有随机性，又具有确定性，两者相互影响。首先，有载调压变压器分接头的档位位置为随机产生，而这一随机值将会对补偿点无功上限/下限容量的确定性求解过程产生影响；其次，每个补偿点无功补偿值是在无功补偿动态区间内随机产生的，而这一随机值又会影响到后续补偿点无功补偿动态区间的构建过程。因此，这种既随机又确定的方法不仅能合理地压缩解空间，而且可将很大部分不可行解自动排除掉，比完全靠随机产生的初始种群更能有效地产生可行解。

3.3 混合启发式搜索算法的新应用

在遗传算法优化过程中，引入模拟退火法、罚因子自适应调整机制及动态灾变算法等现有优秀的启发式算法，形成混合启发式搜索算法，将其应用于含分布式电源的配网无功运行优化这一领域，以改善算法寻优质量及精度。

（1）在遗传算子杂交过程中融入智能启发式思想[14]，使子代个体更加多样化，更具有方向性。

（2）为避免评估淘汰机制出现种群“家族垄断”的现象，本文在个体生存策略中引入了模拟退火思想[15]，使得在种群进化初期适应度低于生存阀值的个体能够以一定的机会存活下来，保证了进化样本的多样性。

（3）本文在电压越限罚因子的取值问题上引入了罚因子自适应调整机制[16]，能使本代中的绝大部分可行解个体适应值优于非可行解。

（4）为解决遗传算法可能存在的“早熟”问题和提高算法的全局搜索性能，本文在收敛判据中引入了保留最优解的灾变技术[9]。

3.4 处理电压约束的两阶段寻优策略

在配电网无功优化中，对于大多数实际系统而言，当仅考虑经济收益时，优化结果能自动使电压满足要求；并且对于这类系统，由于没有考虑电压约束减小了搜索空间和计算负担，反而更能保证解的质量和计算效率。为此，本文采用一种两阶段考虑电压约束的寻优策略[9]，每一个初始解的产生都采取“补偿-电压校验-补偿”的循环搜索方法，使形成的初始种群绝大部分为满足电压要求的可行解。

3.5 算法收敛及流程

本文算法的收敛需依次满足以下4项判据，分别如下。

判据1：如果一代中的解平均适应度与最优适应度的相对误差小于0.001，并且连续10代中的最优解保持不变。

判据2：种群进化代数大于预先设定的最小进化代数。

判据3：若为算法的第一阶段（即不考虑电压约束），各节点电压自动满足要求。

判据4：若已达到最大允许遗传代数，则给用户提示信息，输出当前最优解，算法结束。

本文所提出的配网无功电压综合协调优化算法总体流程如图1所示。

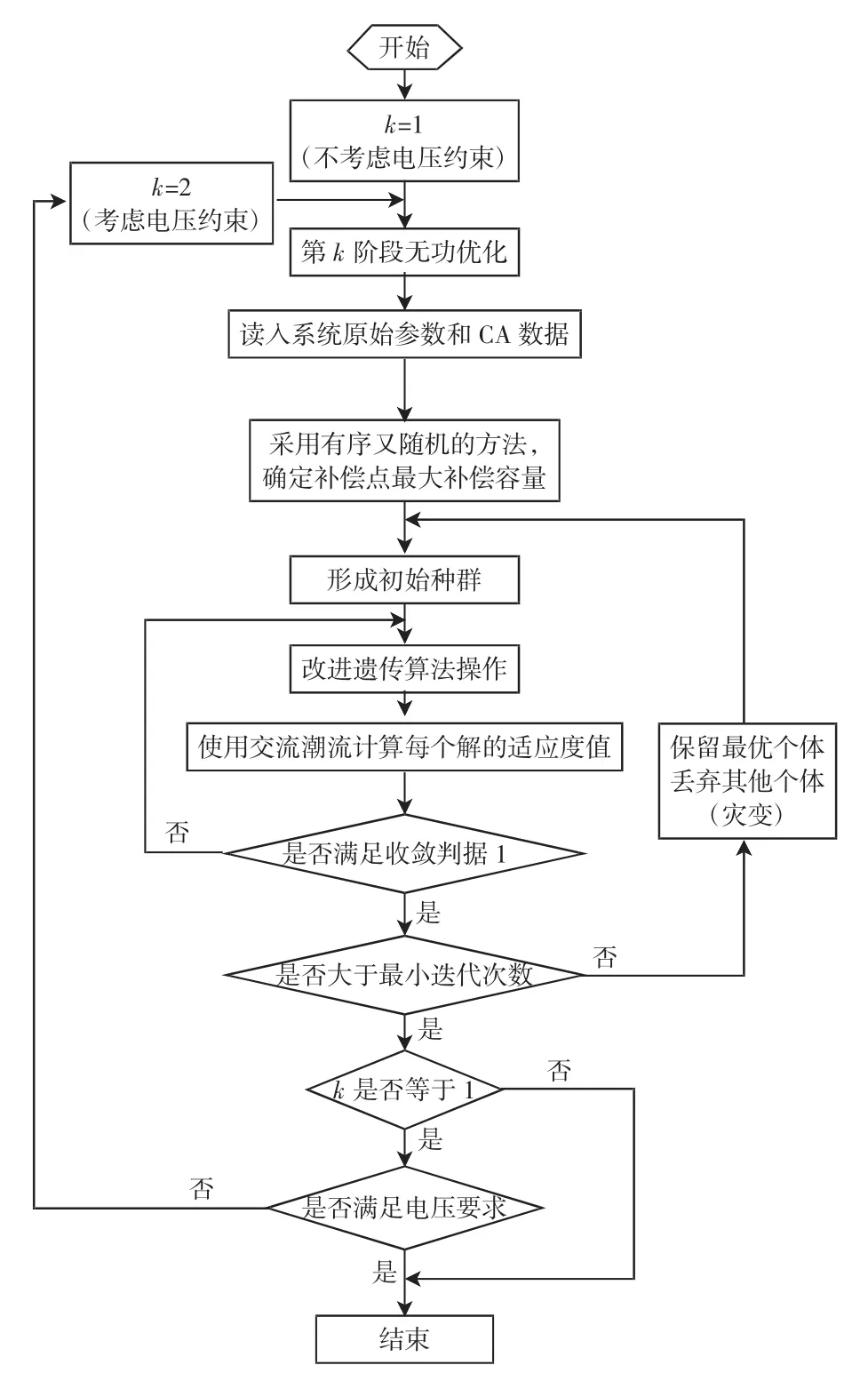
图1 配网无功电压综合协调优化算法流程Fig.1 Flow chart of the coordinate optimization algorithm for reactive power and voltage in distribution networks

4 算例分析

现采用IEEE33节点网络进行算法的仿真测试，如图2所示。

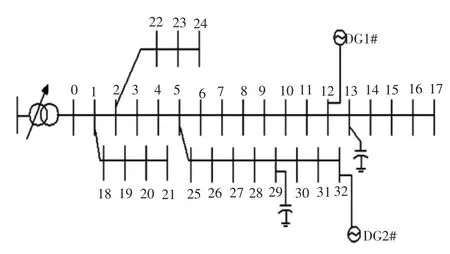
图2 IEEE33节点网络Fig.2 IEEE33 node network

有载调压变压器一台，SN=31.5 MVA，110±8× 1.25%/10.5。在节点13和节点29处分别安装馈线并联电容器若干组。在节点12和节点32处各有1座小型水电站，编号分别为DG1#、DG2#，该类型DG既可提供无功，又可吸收无功。具体参数设置见表1和表2。

表1 IEEE33节点网络中分布式电源参数设置Tab.1 Parameters of distributed generations of IEEE33 node network

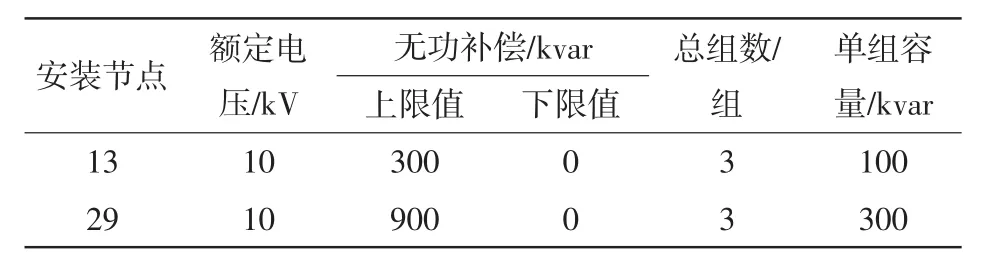
表2 IEEE33节点网络中无功补偿电容器参数设置Tab.2 Parameters of capacitors of IEEE33 node network

本文在“最大负荷最小发电”和“最小负荷最大发电”等两种配网运行方式下，采用改进混合遗传算法进行无功电压优化计算分析，设置最大迭代次数为300代，最小迭代次数为50代，网络节点电压约束为[9.3，10.7]kV。

4.1 最大负荷最小发电

这种运行方式可视为系统重载可能引起低电压的情况，无功优化前后的相关指标对比情况详见表3、表4和图3。

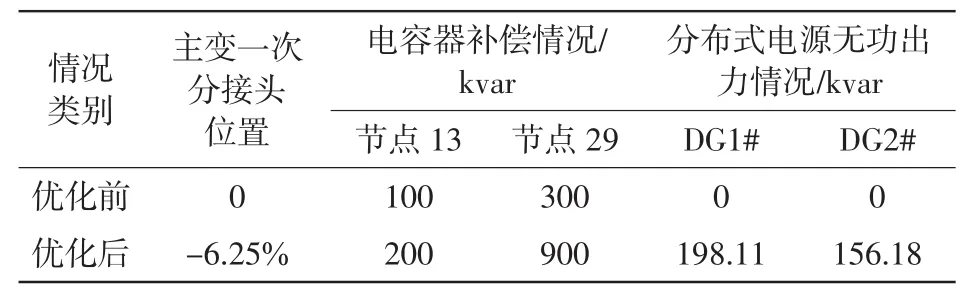
表3 IEEE33节点网络无功优化前后的设备状态对比Tab.3 Comparison of device status before and after the reactive power optimization

表4 IEEE33节点网络无功优化前后的网损对比Tab.4 Comparison of real power losses before and after the reactive power optimization

由表3、表4可以看出：IEEE33节点系统经过无功优化计算后，主变一次分接头调至-6.25%，节点13、节点29处的电容器补偿容量分别多投入100 kvar、600 kvar，节点12、节点32处的DG1#、DG2#无功出力分别为198.11 kvar、156.18 kvar，网络损耗减少了0.200 72 MW，降损效果较好。经过优化后，所有节点电压质量满足要求，如图3所示。

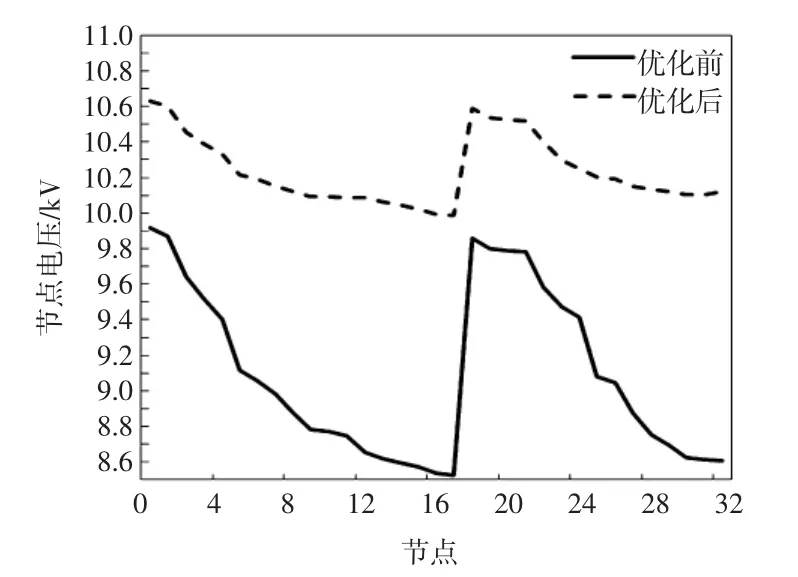
图3 IEEE33节点网络无功优化前后的电压质量对比Fig.3 Comparison of voltages before and after the reactive power optimization

结合表3、表4和图3的结果进行分析可得：在系统大负荷的情况下，流经线路的电流较大，网络损耗主要由线路和变压器中串联支路电阻损耗引起，其值与节点电压的平方近似成反比关系；通过调低主变分接头档位、投入部分电容器组和增加分布式电源无功出力等多种手段，尽可能地提高节点电压，进而使得网络降损效果最大；同时算法中考虑了节点电压约束，在降损效果最大的同时节点电压均不能越上限，保证电网安全、经济地运行。

4.2 最小负荷最大发电

这种运行方式可视为系统轻载、潮流倒送可能引起高电压的情况，无功优化前后的相关指标对比情况详见表5、表6和图4。

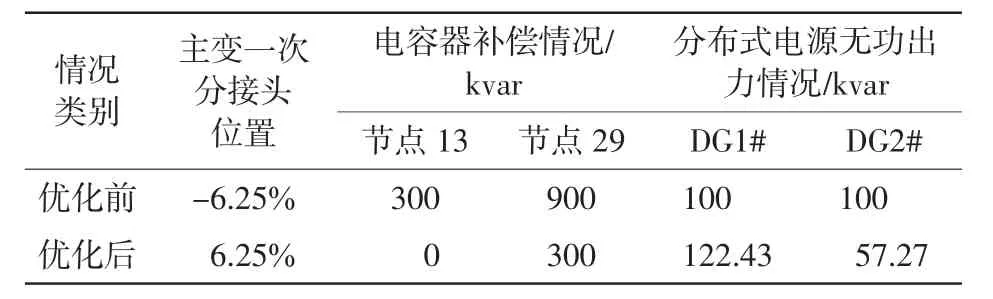
表5 IEEE33节点网络无功优化前后的设备状态对比Tab.5 Comparison of device status before and after the reactive power optimization

表6 IEEE33节点网络无功优化前后的网损对比Tab.6 Comparison of real power losses before and after the reactive power optimization

由表5、表6可以看出：与“最大负荷最小发电”运行方式相比，IEEE33节点系统经过无功优化计算后，主变一次分接头由-6.25%调至6.25%，节点13处电容器组退出运行，节点29处电容器补偿容量减少至300 kvar，节点12处DG1#无功出力为122.43 kvar，节点32处DG2#无功出力减少至57.27 kvar，网络损耗减少至0.033 59 MW，降损效果良好。经过优化后，所有节点电压的数值均变小，如图4所示。

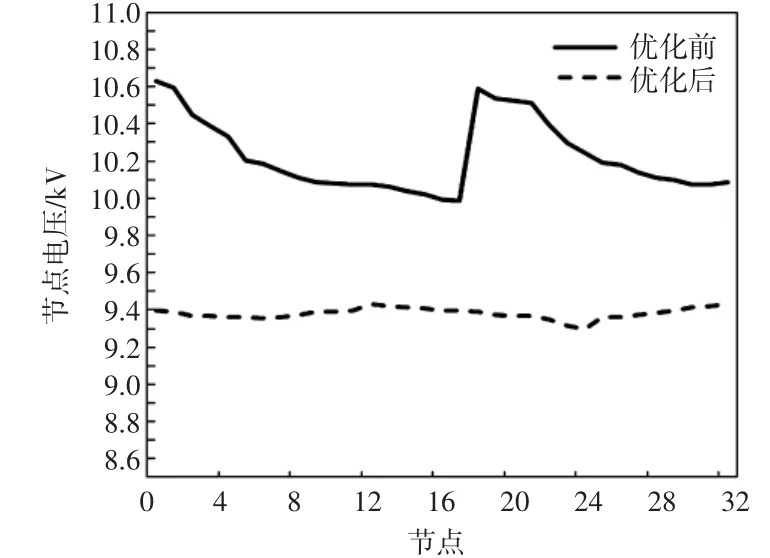
图4 IEEE33节点网络无功优化前后的电压质量对比Fig.4 Comparison of voltages before and after the reactive power optimization

结合表5、表6和图4的结果进行分析可得：在系统轻载的情况下，流经线路的电流较小，网络损耗主要由线路和变压器中对地并联支路的电阻损耗引起，其值与节点电压的平方近似成正比关系；通过调高主变分接头档位、切除部分电容器组和调节分布式电源无功出力等多种手段，尽可能地降低节点电压，使得网络降损效果最大；同时算法中考虑了节点电压约束，在降损效果最大的同时节点电压均不能越下限，保证电网安全、经济地运行。

另外需说明的是，本文采用的补偿容量动态区间法与固定上、下限法（即将节点处所安装的补偿容量作为其上、下限）相比，在算法效率上具有一定的优势。就本文算例而言，经计算得知：动态区间法相比于固定上下限法，在最优性相当的情况下，其计算速度提高近20%～30%，尤其在最小负荷最大发电情况下效果更加明显。分析其原因为：在负荷较小时，各节点需补偿的电容器组数小于其安装组数，因此采用动态区间法可依负荷情况合理下调补偿上限值，有效压缩解空间，提高可行解的生成概率，缩短遗传算法的迭代次数、潮流迭代次数及总的计算时间。

5 结论

（1）本文提出一种综合考虑DG、有载调压变压器分接头及并联电容器组协调控制问题的配电网无功电压运行优化模型及算法。

（2）在满足节点电压要求和配电网经济运行条件下，本文提出的节点补偿容量动态区间将随着其他节点无功补偿及主变分接头档位的随机调节而实现双向动态变化，有效压缩了算法搜索空间。通过IEEE33算例仿真，验证了提出的优化算法是可行的，具有较强的收敛性和寻优质量。

（3）本文重点研究含DG的配电网静态无功优化问题，未计及设备动作次数约束。下一阶段将对计及设备动作次数约束的配电网动态无功优化进行深入研究。

[1]杨晓萍，张强，薛斌，等（Yang Xiaoping，Zhang Qiang，Xue Bin，et al）.考虑静态电压稳定性的多目标无功优化（Multi-objective reactive power optimization with static voltage stability）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：138-144.

[2]李惠玲，盛万兴，孟晓丽（Li Huiling，Sheng Wanxing，Meng Xiaoli）.基于改进小生境遗传算法的配电网全网无功优化（General reactive power optimization of whole distribution network based on improved Niche genetic algorithm）[J].电网技术（Power System Technology），2009，33（4）：34-37，50.

[3]刘红文，张葛祥（Liu Hongwen，Zhang Gexiang）.基于改进量子遗传算法的电力系统无功优化（A reactive power optimization method based on improved quantum-inspired genetic algorithm）[J].电网技术（Power System Technology），2008，32（12）：35-38，50.

[4]许文超，郭伟（Xu Wenchao，Guo Wei）.电力系统无功优化的模型及算法综述（Summarize of reactive power optimization model and algorithm in electric power system）[J]．电力系统及其自动化学报（Proceedings of the CSUEPSA），2003，15（1）：100-104.

[5]Liang Ruey-Hsun，Cheng Chen-Kuo.Dispatch of main transformerULTCandcapacitorsinadistributionsystem[J]. IEEE Trans on Power Delivery，2001，16（4）：625-630.

[6]赵登福，刘昱，夏道止（Zhao Dengfu，Liu Yu，Xia Daozhi）.考虑开关动作次数约束的配电网无功电压控制方法的研究（Reactive power/voltage control of distribution system considering the constraint of the maximum allowable number of switching operations）[J].西安交通大学学报（Journal of Xi’an Jiaotong University），2003，37 （8）：783-786.

[7]胡泽春，王锡凡（Hu Zechun，Wang Xifan）.配电网无功优化的分时段控制策略（Time-interval based control strategy of reactive power optimization in distribution networks）[J].电力系统自动化（Automation of Electric Pow－er Systems），2002，26（6）：45-49.

[8]李林川，李俊元，武文杰（Li Linchuan，Li Junyuan，Wu Wenjie）.考虑变压器分接头动作次数限制的综合无功优化（Synthetic reactive power optimization considering constraints of maximum allowable number of tap changer operations）[J].中国电力（Electric Power），2005，38（2）：49-52.

[9]赵俊光，王主丁，张宗益，等（Zhao Junguang，Wang Zhuding，Zhang Zongyi，et al）.基于节点补偿容量动态上限的配电网无功规划优化混合算法（A dynamic upper limit to node compensation based hybrid optimization algorithm for reactive power planning in distribution networks）[J].电力系统自动化（Automation of Electric Power Systems），2009，33（23）：69-74.

[10]张丽（Zhang Li）.包含分布式电源的配电网无功优化（Reactive power optimization for distribution system with distributed generators）[J].电工技术学报（Transactions of China Electrotechnical Society），2011，26（3）：168-174.

[11]李晶，王素华，谷彩连（Li Jing，Wang Suhua，Gu Cailian）.基于遗传算法的含分布式发电的配电网无功优化控制研究（Research of reactive power optimization control in distribution networks based on genetic algorithm）[J].电力系统保护与控制（Power System Protection and Control），2010，38（6）：60-63.

[12]陈琳，钟金，倪以信，等（Chen Lin，Zhong Jin，Ni Yixin，et al）.含分布式发电的配电网无功优化（Optimal reactive power planning of radial distribution system with distributed generation）[J].电力系统自动化（Automation of Electric Power Systems），2006，30（14）：20-24.

[13]Wang Zhuding，Shokooh F，Jun Qiu.An efficient algorithm for assessing reliability indexes of general distribution systems[J].IEEE Trans on Power Systems，2002，17（3）：608-614.

[14]江道灼，张树森，章鑫杰（Jiang Daozhuo，Zhang Shusen，Zhang Xinjie）.改进遗传算法在无功优化算法中的应用（The application of improved algorithm in reactivepower optimism）[J].浙江理工大学学报（Journal of Zhejiang Sci-Tech University），2006，23（4）：442-445.

[15]刘科研，盛万兴，李运华（Liu Keyan，Sheng Wanxing，Li Yunhua）．基于改进遗传模拟退火算法的无功优化（Research on reactive power optimization based on improved genetic simulated annealing algorithm）[J].电网技术（Power System Technology），2007，31（3）：13-18.

[16]张粒子，舒隽，林宪枢（Zhang Lizi，Shu Jun，Lin Xianshu）.基于遗传算法的无功规划优化（Reactive power planning based on genetic algorithm）[J].中国电机工程学报（Proceedings of the CSEE），2000，20（6）：5-8.

Hybrid Algorithm for Reactive Power Optimization in Distribution Networks with Distributed Generations

WANG Wei-ping1，WANG Zhu-ding1，ZHANG Yun2，WANG Kai3，SHEN Wei3，ZHAO Jun-guang4
（1.State Key Laboratory of Power Transmission Equipment&System Security and New Technology，Chongqing University，Chongqing 400030，China；2.Hangzhou Electric Power Design Institute Co.，Ltd.，Hangzhou 310009，China；3.Hangzhou Electric Power Bureau，Hangzhou 310009，China；4.Chongqing Power Company Jiangjin Power Supply Bureau，Chongqing 402260，China）

In order to make reactive power and voltage control in distribution networks at a reasonable leveland solve the problem that the varcompensationupper orlower-limit of equipment capacity may result in larger space of solution search，a hybrid optimization algorithm for reactive power and voltage of distribution networks with distributed generation based on changeablerange of node compensation capacity is presented in this paper.Moreover，a simulated annealing，an adaptive adjustment mechanism of penalty factors and a dynamic disaster mechanism are employed in the late period of population evolution，which improves the quality and accuracy of search.The simulation results and analysis demonstrate the efficiency and practicality of the proposed algorithm.

distribution networks；reactive power and voltage control optimization；distributed generation；changeablerange of node compensation capacity；improved genetic hybrid algorithm

TM714.3

A

1003-8930（2013）06-0093-08

王卫平（1985—），男，硕士研究生，研究方向为电力系统规划与运行优化。Email：wang6527@163.com

2012-04-28；

2012-06-27

科学技术部科技型企业技术创新基金项目（06C26225110507）

王主丁（1964—），男，博士，教授，研究方向为电力系统规划、运行与优化。Email：mmluck@yahoo.com

张 昀（1976—），女，硕士，工程师，从事电力设计工作。E－mail：zy51231411@gmail.com