“负荷趋势+混沌”预测法的改进

穆青青，伍永刚，杨纪明

（1.汉江集团信息中心，丹江口 442700；2.华中科技大学水电与数字化工程学院，武汉 430074；3.丹江口水力发电厂，丹江口 442700）

“负荷趋势+混沌”预测法的改进

穆青青1，伍永刚2，杨纪明3

（1.汉江集团信息中心，丹江口 442700；2.华中科技大学水电与数字化工程学院，武汉 430074；3.丹江口水力发电厂，丹江口 442700）

“负荷趋势+混沌”预测法，将负荷拆分成“负荷趋势”和“混沌”部分。但其在分离负荷趋势部分时提取过量，混沌预测模型存在累积误差。针对这些问题文中根据周期与混沌的频谱特性，通过快速傅里叶变换确定周期分离的量；根据邻近点是否是预测值，对加权一阶局域法多步预测的邻近点权重增加因子进行修正；同时对剩余负荷为随机噪声的情况进行了处理。通过对海南地区负荷进行预测，验证了改进后的方法在预测精度方面有明显提高。

短期负荷预测；负荷趋势；混沌；加权一阶局域法；邻近点权重

短期负荷预测是指对未来1天到一周的负荷预测。它是电力系统安全经济运行的基础，对地区或电网范围内的电力规划有着重要作用。为了提高电网的安全性和经济性，改善供电质量，短期负荷预测要有尽可能高的预测精度。

目前电力系统短期负荷预测的基本方法分成两大类。第一类是只依据历史记录进行预测，如时间序列法、混沌预测法、经验模态分解EMD（empirical mode decomposition）法及希尔伯特-黄变换HHT（Hilbert-Huang transform）方法等。时间序列法是根据负荷的发展规律来进行预测的，所需数据少，计算简单[1]；混沌预测方法是利用混沌吸引子在不同层次间的自相似性进行混沌系统的短期预测，它通过相空间重构来近似恢复原来的多维非线性混沌系统；EMD方法是将数据分解为有限几个独立的、近乎周期性的内在模式函数及余项，利用各个分量来进行预测的[2]。HHT方法是对EMD方法的一种改进，是有EMD和Hilbert变换两部分组成的，它是利用一阶差分算法消除EMD模态混叠，通过对各分量的频谱计算和观察，将低频分量进行重构，选取合适模型对各个分量进行预测[3]。第二类方法是考虑天气和社会因素等影响的因果性方法，如采用相似日法、神经网络法、神经网络与替他方法的结合如小波变换、粒子群等，以及第一种方法与负荷影响因素相结合的方法，如基于EMD与因素影响的负荷分析法[2]。虽然第二类方法通常优于第一类方法，但由于预测时所需要的天气等信息也是预测值，一旦天气预报不准确，则可能会引起更大的负荷预测误差；同时第二类方法也是在第一类方法的基础上结合负荷影响因素而产生的。因此只考虑负荷历史记录的预测方法，仍然需要进行深入的研究[4]。

只依据负荷历史记录进行短期负荷预测时，提高预测精度的方法之一，是深入研究历史负荷的规律，并采用多个子模型进行预测[4]。大量的研究[4-6]表明负荷具有周期、混沌、随机的特性，因此很多学者[4-6]将负荷分为3部分即周期部分、混沌部分和随机噪声部分，对这3部分分别建立子模型进行预测，最后再叠加起来即得预测负荷。在目前的研究中，文献[4]发现负荷是以双周期行为（24 h和12 h）为主的，双周期以外的剩余成分是以混沌为主，故为简化预测模型，提出“双周期+混沌”法。该方法采用双周期加混沌这2个子模型来进行负荷预测，具有更高的预测精度和可靠性。

本文基于“双周期+混沌”法在正常日负荷的情况下对负荷进行研究分析，发现负荷除了具有双周期成分外，还有其他周期成分6 h等。文献[4]也根据负荷的多周期性，在文献[7]中提出了“负荷趋势+混沌”预测方法，此方法是“双周期+混沌”法的进一步研究，将负荷的多周期部分即负荷基本趋势提取出来，然后对剩余负荷进行混沌预测，本文就是基于这种方法进行研究的。因此本文采用文献[8]里提出的快速傅里叶变换FFT（fast Fourier transform）将负荷的全部周期成分分离出来，得到了日负荷基本的变化趋势，然后对剩余混沌时间序列采用广泛应用的加权一阶局域法多步预测[9]模型进行预测。

同时之前的研究中[4，7]存在以下两个问题：问题一是在分离多周期部分时周期频率处是全部提取，因负荷序列是周期、混沌、随机的混合，全部提取会引起周期分离量过多，针对此问题文中提出要考虑并确定分离的量。问题二是在运用加权一阶局域法多步预测[9]模型对剩余序列进行预测时，会用到预测值，存在累积误差，针对此问题本文提出在邻近点的权重上增加因子进行自适应修正，消减因预测值代入计算所带来的累积误差。同时本文对剩余序列为随机噪声的情况进行分析处理。

1“负荷趋势+混沌”法预测原理

1.1 电力负荷组成成分及分离方法

实际电力负荷包含着周期性，混沌及随机性，故负荷可被分为3部分：多周期有规律部分即负荷趋势部分，混沌部分和随机噪声部分。在对负荷进行预测时，要分别将这3部分分离出来然后单独建立模型进行预测，最后叠加起来即得预测负荷，其原理如图1所示。在目前的研究中，为简化模型，文献[4]提出了“负荷趋势+混沌”法，是将负荷分为负荷趋势部分和剩余混沌部分，然后分别建立子模型进行预测，最后再叠加起来。负荷趋势部分就是负荷的多周期部分，因在分离周期部分时因任何一个信号都可以用一系列的正弦波来表示，故考虑运用FFT分离出周期性的有规律的部分，对负荷趋势部分可直接外推即可得到预测值。在对剩余负荷进行混沌预测时，一般情况下一阶加权局域法多步预测模型被广泛用于混沌预测。

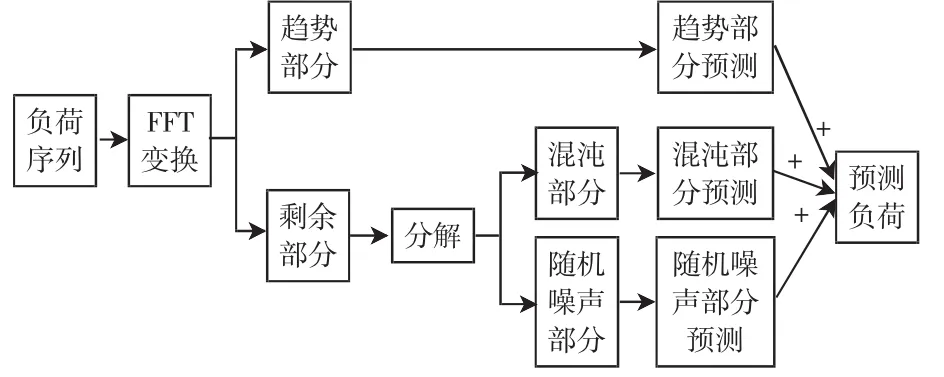
图1 负荷预测原理Fig.1 Schematic diagram of load forecasting

1.2 分离负荷趋势部分

离散傅里叶变换DFT（discrete Fourier transform），尤其是快速傅里叶变换（FFT），已作为普遍应用的数字信号处理技术广泛应用于电力系统的频谱分析中。任何一个时间序列都可分解为一系列的正弦波。故可对负荷时间序列进行FFT分析。通过对负荷序列进行FFT变换，在频域中分析负荷的频谱特性，然后将具有周期特性的频率值经FFT反变换到时域中，得到负荷的周期部分。对海南电网负荷值进行FFT变换，其结果如图2（a）所示，将负荷的频谱图放大即得到图2（b）。从图2（b）中看到实际电力负荷在频域中具有多周期特性，主要的周期频率为0.010 4 Hz和0.020 8 Hz，则在实际电力负荷的主要周期为1/0.010 4和1/ 0.020 8，即为96点和48点。因海南实际电力负荷一天24 h 96点，故实际的负荷周期为一天24 h和12 h即是双周期，此说明海南电网电力负荷具有很明显的双周期性。同时从图中还可看到负荷还有其他不太明显的周期成分如6 h等，故本文在双周期分离的基础上，通过FFT将负荷的所有周期部分均提取出来，且通过自动分离办法将其多周期部分提取出来，得到负荷趋势部分。

图2 负荷频谱图Fig.2 Frequency spectra of the load

1.3 剩余混沌部分预测

通过FFT方法将负荷的负荷趋势部分分离出来，得到剩余负荷，因负荷除具有多周期特性外还具有混沌特性，则对剩余负荷进行混沌判定为混沌，通过混沌预测方法对剩余负荷进行预测，在混沌预测方法中基于相空间重构的加权一阶局域法多步预测被广泛应用。

1.3.1 相空间重构理论

相空间重构理论认为系统任意分量的演化是由与之相互作用的分量决定，因此这些相关分量的信息就隐含在任一分量的发展过程中。这样，可以从某一分量的一批时间序列数据中提取和恢复出系统原来的规律[6]。要对混沌时间序列进行预测，首先要对时间序列进行相空间重构。

假设观测到的混沌时间序列为xk，k=1，2，…，N。相空间模式为

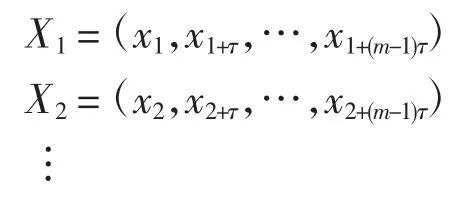
式中：τ为时间延迟；m为嵌入维数；相点总数n= N-（m-1）τ；Xi为重构相空间相点，i=1，2，…，n。

嵌入维数的计算：1983年Grassberger和Procaccia提出了从时间序列计算吸引子关联维数的G-P算法[10]。如果随着嵌入维数m升高，关联维数达到饱和，此时的m为时间序列的重构相空间的嵌入维数。

延迟时间的计算：运用复自相关法[11]计算延迟时间。

1.3.2 加权一阶局域法多步预测模型

利用上述式（1）构造相空间，设中心点为XM，他的邻近点为XMi，i=1，2，…，q。这些邻近点演化k步后的的相点为XMi+k。则加权一阶局域法多步预测模型为

式中，ak，bk是通过加权最小二乘法得到的。

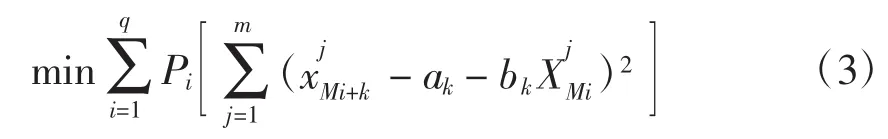
式中，Pi为权重系数，是中心点的第i个邻近点的权重，其计算式为

式中，C为参数，一般情况下取1。根据求得的ak，bk，代入k步预测式（2），即可得到演化k步后的相点预测值XM+k为

式中，XM+k中的第m个元素xM+K+(m-1)τ即为原序列的k步预测值XN+k。

1.4“负荷趋势+混沌”预测算法

“负荷趋势+混沌”预测方法是将负荷分为多周期（负荷趋势）部分和剩余混沌部分，分别对其进行预测，最后再叠加起来即得到预测负荷，其计算步骤如下：

步骤1对负荷序列进行FFT变换到频域中，然后将其有规律（周期）部分通过FFT反变换分离出来，得到基荷即负荷的趋势部分；

步骤2原有负荷序列减去负荷趋势部分得到剩余负荷，对剩余负荷进行计算延迟时间和嵌入维数，构造相空间，然后计算其最大Lyapunov指数；

步骤3最大Lyapunov指数大于0，则剩余负荷为混沌序列，采用第2.3节的加权一阶局域法多步预测模型进行预测，得到剩余序列的预测值；

步骤4剩余序列的预测值加上负荷趋势部分直接外推得到的值，即得到所需的预测负荷。

2 算法改进

在之前的研究中分离负荷趋势部分时是对多周期部分对应的频率处全部提取，会引起提取过多，因负荷是周期、混沌、噪声的混合，将负荷变换到频域中的值是各个成分共同作用的结果；在运用加权一阶局域法多步预测模型进行预测时邻近点在多步之后的点可能是预测值，会引起累积误差；同时序列不为混沌为随机噪声时应怎样处理，基于以上存在的问题，提出如下改进方法。

2.1 负荷趋势部分信号自动分离及分离量

（1）自动分离的办法：因时间序列中有周期部分，需要运用FFT变换到频域中，然后再将某些具有周期性的频域值反变换回去得到周期部分。这就需要将频域中幅值较大的自动分离出，因这部分就是具有周期的有规律的部分。则设定一个阈值，大于此阈值的则分离出来，小于此阈值的认为在该频率处不是主要成分。此阈值的设定为：首先将各个频率处的值按从大到小的顺序排序，然后只取前面的m=n/2×0.5（n为FFT变换后的值的总个数）个较大的幅值，然后求这m个值的均值，此均值即为阈值。

（2）分离周期趋势部分某个频率处的量的问题：首先因为此频率处的值较大满足上面阈值的条件，说明相比较混沌和噪声信号此处为负荷的主要频率成分，所以才将其分离出来。因为混沌信号与噪声信号都是连续分布的宽谱，且实际中的混沌信号与噪声信号的频谱差别很小，故确定提取周期频率处幅值的量的方法是：因为在周期频率处其幅值主要是周期部分的贡献，混沌及随机的贡献较小，故可对要分离的频率处首先设一个权值为0.85，然后一直增加权值，直到剩余的此频率处的值与此频率的前一个和后一个频率处的值相当[（Qsi-Qi-1）/Qi-1+（Qsi-Qi+1）/Qi+1]/2＜0.002即可。其中Qsi为分离的频率处剩余的幅值，Qi-1为分离频率处的前一个频率处的幅值，Qi+1为分离频率处的后一个频率处的幅值。

2.2 加权一阶局域法多步预测的改进

在第2节中式（3）和式（4）没有考虑到邻近点在多步之后的点可能是之前的预测值，代入算法中预测，会引起累积误差。针对此问题，本文在邻近点的权重上增加一个因子进行自适应修正。其修正办法如下。

（1）当k步预测时，若中心点的邻近点在k步演化之后的那个点的序号K＞中心点序号M，则修正为

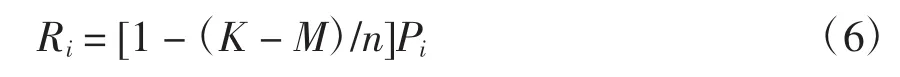
式中：n为预测的点数，Pi为式（4）计算所得的原始的权重，此时因用到预测值考虑到会有累积误差，故消减原有的权重。

（2）若中心点的邻近点在k步演化之后的那个点的序号K=中心点序号M，则修正为

此时是保持原有的权重。

（3）若中心点的邻近点在k步演化之后的那个点的序号K＜中心点序号M，则修正为

此时未用到预测值，用到的是序列的实际值，故增加原有的权重。则最终的权值为

在本文中此n值是10。

2.3 剩余负荷为随机噪声的处理

对剩余负荷计算最大Lyapunov指数进行混沌判定，判别为混沌时，由于剩余部分中还含有噪声部分，则这时是噪声、混沌的混合，需要进行分离，然后再进行预测。但若剩余负荷不为混沌为随机噪声时也要对噪声部分进行处理。具体处理方法如下。

2.3.1 对噪声的处理

对剩余负荷进行混沌判定若不为混沌时，由于之前已经将负荷趋势部分分离出来，而时间序列一般是周期、混沌及噪声的混合，故此时剩余序列不为混沌，则应是噪声部分。噪声具有随机性，是测量设备或是其他外界因素原因而带来的噪声，它是不可预测的，一般实际中时间序列都含有噪声。对噪声处理时可考虑去剩余噪声序列的均值，则可将其均值作为剩余噪声序列的预测值。

2.3.2 剩余负荷为混沌时去噪的处理

当对剩余序列进行混沌判定为混沌时，则说明剩余序列具有混沌特性。则由于噪声的最大Lyapunov指数时接近0的数值，而混沌时间序列的最大Lyapunov指数时大于0的，故若对剩余序列进行混沌判定时最大Lyapunov指数大于0为混沌时，则剩余序列中可能还有噪声部分，这时需要对剩余序列进行处理。

因噪声是不可预测，而混沌时间序列可以根据混沌预测方法进行预测，对混沌剩余序列处理时需要将噪声去掉，将混沌部分提取出来。对混沌部分进行混沌预测，对噪声部分运用上述噪声处理的方法。小波变换时目前许多科学和工程技术领域中很热门的问题之一。它能在时频域中给出信号的良好的局部表示，非常适合对信号进行特征提取。尽管混沌信号与噪声信号的频谱都是连续分布的宽谱，但混沌信号的奇异性与噪声的奇异性在小波变换下有着截然不同的表现[12]。故本文采用小波变换提取混沌部分，实现剩余序列的混沌噪声分离。同时对分离后的混沌部分和噪声部分计算最大Lyapunov指数来验证分离的正确性。

对一个Lorenz混沌时间序列，其中σ=10，γ= 28，b=8/3。并取x、y、z的初始值为11、5、8。其中取x方向的1 000个点作为研究对象，在此混沌时间序列的基础上在叠加上随机信息构成混沌噪声混合时间序列，如图3（a）所示。对此混合信号进行小波变换，分离出的混沌及噪声信号如图3（c）、（d）所示。

从图中可以看到混合信号经小波去噪后基本保持了原有混沌序列的变化趋势。对混合信号中分离出的混沌部分和剩余噪声部分分别进行Lyapunov指数计算，得到分离出的混沌部分为0.024 04，剩余噪声部分为0.000 808 7。可以看出提取混沌后的剩余部分的最大Lyapunov指数接近0，说明剩余部分为噪声，同时也说明利用小波变换成功的实现了混沌与噪声的分离。同时对混合信号及原始混沌序列与随机序列进行最大Lyapunov指数计算分析，得到混合信号的为0.014 7，原始混沌信号为0.027 3，原随机序列为0.000 749 3。由此说明分离后的混沌信号比原始混合信号的最大Lyapunov指数大，也验证了分离的正确性。

3 算例分析

对海南地区2008年6月选取一周的负荷数据，对其进行预测。在选取历史样本时，本文通过对选取历史样本的长短对负荷预测的影响进行了分析比较，发现选取历史数据为20天时得到的预测负荷较好，故本文选取预测日之前的20天为历史负荷数据（一天96点）。因负荷具有周期性，故对历史数据进行均值的处理，得到一天96点的均值序列，对此序列进行FFT变换，利用上述改进算法得到一天所含的负荷趋势（多周期）部分，然后这20天历史数据分别减去这每天的有规律部分得到剩余负荷，对剩余负荷计算得到其相空间的嵌入维数m为12，延迟时间τ为27，其最大Lyapunov指数为0.001 221 096 6（大于0），说明剩余负荷为混沌序列具有混沌特性。

图3 混沌噪声混合信号分离出混沌信号及噪声Fig.3 Chaos signal and noise seperated from the mixed signals

对剩余负荷运用小波去噪后其最大Lyapunov指数为0.001 147 66，去除的噪声的最大Lyapunov指数为0.010 42，说明这部分是混沌部分，不可去除，则剩余负荷主要是混沌序列。利用上述改进的混沌算法对剩余负荷进行预测，得到预测值再加上周期部分的直接外推值得到海南电网负荷的预测值。

结合海南地区的误差指标，本文选用5种误差指标：日最高负荷误差，日最低负荷误差，电量误差，均方根误差，平均相对误差。海南电网的一周预测结果误差见表1所示，并与改进前的“负荷趋势+混沌”方法的预测结果进行比较。其中6月17日96点负荷的预测结果和改进前的比较如图4所示。

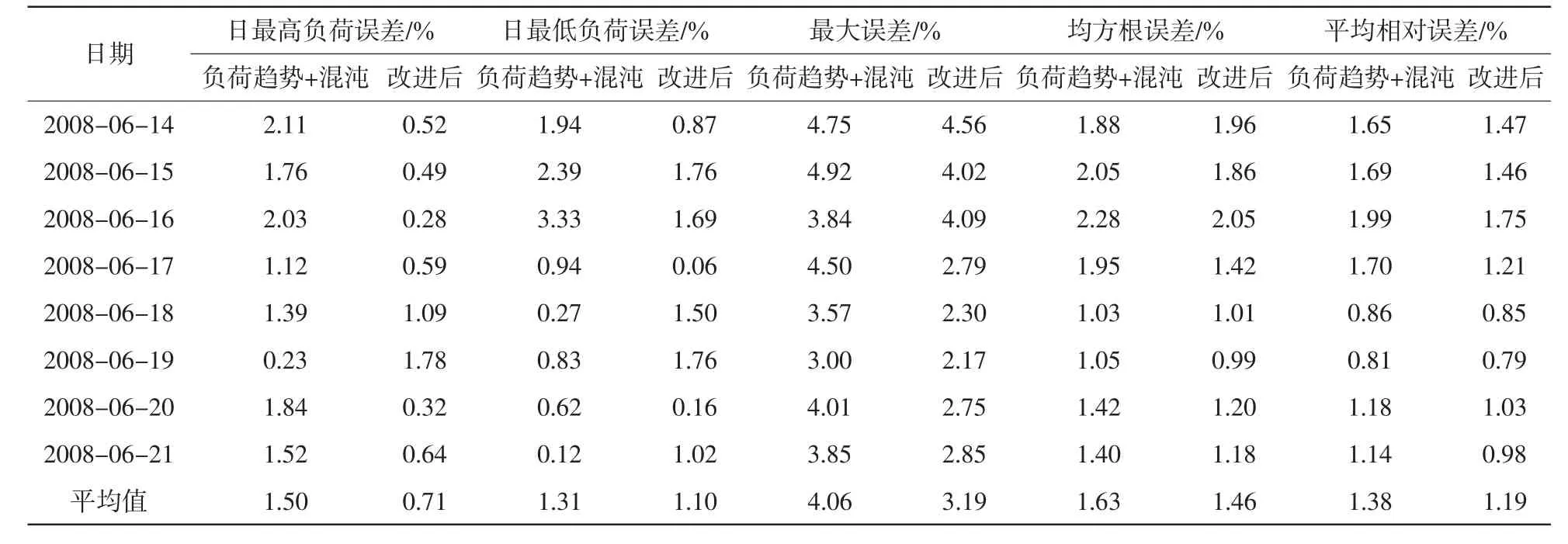
表1 预测负荷的误差指标Tab.1 Error indicators of forecasting load

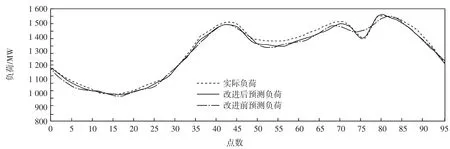
图4 6月17日的改进前后预测结果对比Fig.4 Comparison between the actual load and the forecasting load on June 17

由表1和图4结果分析可见：

（1）从各天误差来看，此种改进方法使预测误差较低，得到了较好的预测结果，提高了预测精度。从每种误差的平均值来看，除最大误差为3.19%外，均可达到1.5%的误差范围。

（2）从5种误差指标来看，日最高负荷误差和最大误差得到了很好的改善，误差较低，能很好地预测负荷的峰值，同时有效地控制了负荷的最大误差，最大误差较小，则负荷的其他误差不会超过最大误差，使得负荷整体的误差都有所改善。均方根误差和平均相对误差也比之前的有所降低。

（3）从图中可看到改进前的方法不能很好地预测负荷序列的峰谷，预测误差较大。通过本文的改进后，其预测结果表明对负荷曲线的峰谷预测较好，同时对日负荷曲线的变化趋势预测的也较好，预测精度明显得到提高。

4 结语

电力系统的短期负荷具有明显的多周期及混沌特性，故“负荷趋势+混沌”预测方法被用于分析研究。但此方法存在周期分离过多和累积误差的问题，针对这些问题本文进行了研究改进，在分离负荷趋势部分时要确定分离的量的问题，对剩余序列运用一阶加权局域法多步预测时在邻近点的权重上增加一个因子进行自适应修正，同时对负荷为随机噪声的情况进行了分析处理。通过对海南电网负荷进行预测分析，结果证明了改进后的方法较改进前的降低了预测误差，提高了负荷的预测精度，取得了满意的结果。本文在进行研究时未考虑负荷的节假日特性，同时负荷还受到天气、温度、湿度、降水量等因素的影响，在对负荷进行预测时需要考虑这些影响因素，在负荷预测方法中相似日法考虑了这些因素，如何将相似日法与本文预测方法结合，将影响负荷的因素进行量化并引入预测模型中，从而提高预测精度。这仍是需要研究的问题。

[1]温权，张勇传，程时杰（Wen Quan，Zhang Yongchuan，Cheng Shijie）．负荷预报的混沌时间序列分析方法（Chaotic time series analysis to load prediction）[J]．电网技术（Power System Technology），2001，25（10）：13-16．

[2]牛东晓，李媛媛，乞建勋，等（Niu Dongxiao，Li Yuanyuan，Qi Jianxun，et al）.基于经验模式分解与因素影响的负荷分析方法（A novel approach for load analysis based on empirical mode decomposition and influencing factors）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（16）：96-102.

[3]白玮莉，刘志刚，彭权威，等（Bai Weili，Liu Zhigang，Peng Quanwei，et al）.一种基于HHT的电力系统短期负荷预测模型 （A power system short-term load forecasting model based on HHT）[J].电力系统保护与控制（Power System Protection and Control），2011，39（2）：55-60，64.

[4]杨正瓴，林孔元，余贻鑫（Yang Zhengling，Lin Kongyuan，Yu Yixin）．短期负荷预报的“双周期加混沌”法中的子模型优选理论探讨（Short term load forecasting by synthesizing double periods and chaotic component：optimization by sub-models）[J]．电网技术（Power System Technology），2003，27（5）：33-36．

[5]杨正瓴，林孔元（Yang Zhengling，Lin Kongyuan）．电力系统负荷记录混沌特性成因的探讨（Discussion on causes of chaos in load records of power systems）[J]．电力系统自动化（Automation of Electric Power Systems），2002，26（10）：18-23．

[6]穆钢，侯凯元，杨右虹，等（Mu Gang，Hou Kaiyuan，Yang Youhong，et al）．一种内蕴误差评价的负荷预报方法（Load forecasting method based on intrinsic error evaluation）[J]．电力系统自动化（Automation of Electric Power Systems），2001，25（22）：37-40.

[7]杨正瓴，张广涛，陈红新，等（Yang Zhengling，Zhang Guangtao，Chen Hongxin，et al）．短期负荷预测“负荷趋势加混沌”法的参数优化（Parameter optimization in synthesizing load trend and chaotic components to short term load forecasting）[J]．电网技术 （Power System Technology），2005，29（4）：27-30，44．

[8]Peng T M，Hubele N F，Karady G G．An adaptive neural network approach to one-week ahead load forecasting[J]. IEEE Trans on Power Systems，1993，8（3）：1195-1203.

[9]郑永康，陈维荣，蒋刚，等（Zheng Yongkang，Chen Weirong，Jiang Gang，et al）．基于混沌理论的短期负荷局域多步预测法 （Local-region multi-steps load forecasting model based on chaotic theory）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（4）：76-79．

[10]黄润生，黄浩．混沌及其应用[M]．武汉：武汉大学出版社，2005．

[11]王抵修（Wang Dixiu）．地学数据分析中的相空间重构预测方法研究（The Study of Phone-Space Reconstruction Prediction Method in Geostatistical Data Analysis）[D]．长春：吉林大学综合信息矿产预测研究所（Changchun：Comprehensive Information Mineral Resources Prediction Research Institute，Jilin University），2008．

[12]王勇，吴旭文（Wang Yong，Wu Xuwen）．混沌信号降噪算法 （The algorithms for noise reduction of chaotic signals）[J]．测试技术学报 （Journal of Test and Measurement Technology），2006，20（2）：179-183.

Improved Method for Short-term Load Forecasting Based on Synthesizing Load Trend and Chaos

MU Qing-qing1，WU Yong-gang2，YANG Ji-ming3
（1.Hanjiang Group Information Center，Danjiangkou 442700，China；2.College of Hydroelectricity and Digitalization Eng.HUST，Wuhan 430074，China；3.Danjiangkou Hydropower Plant，Danjiangkou 442700，China）

The power load series can be divided into two components by the forecasting method of synthesizing load trend and chaos，which namely load trend and chaotic component.However，the part of periodic frequency is totally extracted，meanwhile，the chaotic prediction model can cause the accumulated error.In this paper，the quantity of seperating periodic part is considered and determined by fast Fourier transform according to the periodic and chaotic spectrum characteristics.The weight of adjacent points which are forecasted by the adding-weight one-rank local-region method are modified by adding a factor according to the adjacent points whether is the predictive value.Meanwhile，it makes an analysis on the rest of the load which is the random noise.Moreover，through the Hainan area load forecasting，the results demonstrate that the proposed method is superior to the previous methods in forecasting accuracy.

short-term load forecasting；load trend；chaos；adding-weight one-rank local-region method；weight of adjacent points

TM715

A

1003-8930（2013）06-0160-07

穆青青（1987—），女，硕士，助理工程师，从事水库调度及电网负荷预测的研究。Email：mqq-510@163.com

2011-05-04；

2012-03-12

伍永刚（1963—），男，博士，教授，博士生导师，从事水库优化运行与控制、自动发电控制（AGC）、电价理论、遗传算法、神经元网络等研究。Email：ygangwu@163.com

杨纪明（1985—），男，本科，助理工程师，从事电厂机组运行和维修。Email：332098331@qq.com