计及电力系统N-1的电压稳定裕度估计方法

张继楠，姜 涛，贾宏杰，赵金利，邱璐璐，孔祥玉，李 鹏

（1.天津大学智能电网教育部重点实验室，天津 300072；2.中国南方电网电力调度控制中心，广州 510623）

计及电力系统N-1的电压稳定裕度估计方法

张继楠1，姜 涛1，贾宏杰1，赵金利1，邱璐璐1，孔祥玉1，李 鹏2

（1.天津大学智能电网教育部重点实验室，天津 300072；2.中国南方电网电力调度控制中心，广州 510623）

该文提出一种N-1下电力系统电压稳定裕度快速估计的新方法。首先给出基于局部量测信息的电力系统电压稳定裕度求解模型；在此基础上，推导并给出利用系统支路断线故障前信息快速估计N-1下的系统电压稳定裕度修正模型；最后对所提方法进行了仿真验证。文中方法物理意义明晰、计算速度快，利用系统当前状态即可快速估算出N-1下的系统电压稳定裕度、准确识别出系统电压薄弱节点、给出丰富的电压稳定裕度信息，New England-39、IEEE-300系统仿真结果验证了所提方法的可行性和有效性。

电压稳定；电压稳定裕度；N-1；局部量测信息

随着负荷需求不断增长，大容量远距离输电不断增加，电力系统的电压稳定问题日益突出[1-2]。特别是近年来世界范围内电压失稳事故频频发生，造成了巨大经济损失和严重社会影响，促使研究、运行人员更加关注系统的电压稳定性[3-4]。为了实时掌握系统电压运行状况，及时采取有效措施预防电压失稳，提高系统运行的安全性和经济性，需对电力系统的电压稳定性实时、快速、准确的评估，在线给出系统当前状态下电压稳定裕度信息[5-11]。

广域量测系统WAMS（wide-area measurement systems）在电力系统中的大规模应用，为电力系统在广域范围内实现系统电压稳定在线监测提供了新手段[12-13]。借助广域量测信息在线监测系统的电压稳定性已成为电力系统电压稳定研究的重要方向[14-15]。文献[16-17]在对电力网络戴维南等效的基础上，采用局部量测信息监视电力系统的电压稳定性；文献[18]借助局部量测信息在线监测电力系统的电压稳定性、识别系统中的电压薄弱节点，并进一步提出基于局部量测电压稳定指标的灵敏度方法来改善系统的电压稳定性。上述方法都是基于戴维南等效来研究系统的电压稳定性，理论上，任一时间断面的电力网络都可以简化为某一节点的戴维南等效电路，可戴维南等效是建立在线性电路基础上的，应用到强非线性、时变的电力系统中，自然会具有一定的局限性。文献[19]针对基于多时间断面的戴维南等效存在参数漂移的问题，利用电力系统同步相量测量装置PMU（phasor measurement unit）连续三次测量到的节点电压、电流信息对由测量转差频率引起的相位角偏移进行校正，根据校正后的节点参数值计算各节点戴维南等效参数，然后根据内外阻抗的比值来分析节点的电压稳定性。但这种完全基于量测信息进行黑箱辨识的戴维南等效参数不具有解析特征，不能定量解析影响戴维南等效参数的关键因素，给出当前状态下系统发生N-1开断后的系统电压稳定信息。同一时间断面下，具有解析表达式的网络等值方程，以显式形式反应了系统中负荷和发电机对戴维南等效参数的影响，可用于研究系统N-1状态下的电压稳定信息，然而在这个过程中，需修改节点导纳矩阵、形成消去联络节点后的收缩节点导纳阵、形成负荷阻抗矩阵和负荷与发电机互阻抗矩阵，计算量大。

针对上述问题，本文提出一种电力系统N-1下的电压稳定裕度快速估计的新方法来监测系统的电压稳定性。首先给出基于局部量测信息的电力系统电压稳定裕度的求解模型；在此基础上，推导并给出N-1下快速估计各种支路断线故障的系统电压稳定裕度修正模型；最后通过算例仿真验证了所提方法的可行性和有效性。

1 电压稳定裕度求解模型

电力系统节点电压方程为

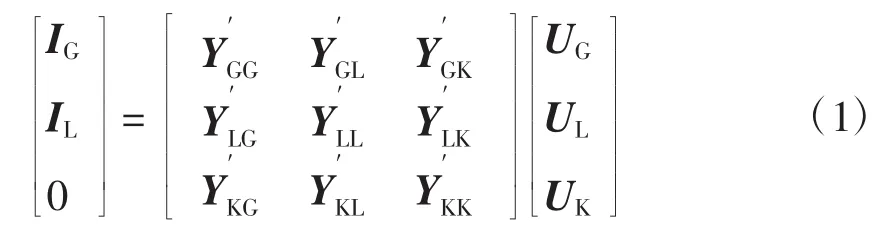
式中：UG和IG分别为发电机节点的电压和电流向量；UL和IL分别为负荷节点的电压和电流向量；UK为系统联络节点的电压向量；，为节点导纳矩阵的子矩阵。

消去网络中联络节点，网络中节点分为两类：一类为网络中全部发电机节点的集合（αG）；另一类为全部负荷节点的集合（αL）。消去联络节点后，式（1）的节点电压方程可变换[20-21]为

令消去联络节点后网络中的负荷节点间的阻抗矩阵ZLL、负荷-发电机阻抗阵ZLG分别为

将式（7）、（8）代入式（2）得

式中：ZLLij为负荷节点i、j间的等效阻抗为负荷节点j注入到网络中的电流；ZLGik为负荷节点i与发电机节点k之间的等效阻抗为发电机节点k的端电压。

其中，

若全网负荷等功率因数增长，则负荷节点i的等效负荷Seqi可进一步表示为式中：S˙0eqi为系统初始状态下负荷节点i的等效视在功率；λ为系统的电压稳定裕度因子。

结合式（15）和（16），由文献[20-21]进一步推导得各负荷节点i的等效临界负荷Screqi为

式中，φeqLLi=-arctan（beqi/aeqi）-arctan（GLLii/BLLii）。

通过式（17）可求出各负荷节点的电压稳定裕度因子λi，由系统电压失稳具有局部性的特点可知：系统电压崩溃通常从系统局部一个或几个负荷节点的电压失稳开始，逐渐扩大到整个系统。其中，首先出现的失稳节点是系统电压最薄弱环节，即系统电压弱节点，弱节点对应着节点电压稳定裕度因子λ最小的节点，即系统电压稳定裕度因子为式中，N为网络中负荷节点的数目。

2 N-1下模型修正

电力系统运行过程中，经常会遇到各种扰动，元件也有可能会发生故障，从而导致某些元件退出运行。研究元件开断情况下系统的潮流分布，计算系统在某些元件开断下的电压稳定裕度，有助于指导运行调度人员及时、合理地采取相关措施消除系统电压失稳发生的可能性，因此研究开断方式下系统电压稳定裕度计算具有十分重要的实际意义。

由于电力系统中元件较多、网络结构复杂，要分析的元件开断情况也非常多，再加上计算要实时进行，所以对电力系统电压稳定裕度的计算速度有较高的要求。电力系统中元件的开断主要包括：支路开断、发电机开断、负荷开断，本文主要关注网络中N-1支路开断时的电压稳定裕度的计算，同时开断前后，系统所有节点应仍连通。对于网络进行N-1开断时，一般而言开断前后负荷功率和发电机的输出功率不变，仅涉及到网络结构的变化，这样仅需对求解模型中式（7）、（8）的ZLL、ZLG进行较少的修正计算，避免重新计算ZLL、ZLG，便可求出系统的电压稳定裕度，可有效提高电压稳定裕度的计算速度。

网络N-1后，系统的负荷阻抗矩阵ZLL、负荷-发电机阻抗矩阵ZLG分别为

式中：ZLL0为支路开断前网络的负荷阻抗矩阵；ZLG0为支路开断前网络的负荷-发电机阻抗矩阵；ZLL1为支路开断后网络的负荷阻抗矩阵的修正矩阵；ZLG1为支路开断后网络的负荷-发电机阻抗矩阵的修正矩阵。

对比式（1）～（8）可知，式（19）修正项ZLL1、ZLG1的计算结果与系统中开断支路的类型有着密切关系，为此本文推导并给出了联络节点间支路开断、联络节点与负荷节点间支路开断、联络节点与发电机节点间支路开断、负荷节点间支路开断、负荷节点与发电机节点间支路开断以及发电机节点间支路开断时各修正矩阵的计算方法。首先定义为式（1）支路开断前的节点导纳矩阵的子矩阵；YGG0、YGL0、YLG0及YLL0为式（2）支路开断前的节点导纳矩阵的子矩阵；分别为支路开断时矩阵的修正矩阵；YGG1、YGL1、 YLG1及YLL1为支路开断时矩阵YGG、YGL、YLG及YLL的修正矩阵。各种N-1下的ZLL1、ZLG1的推导结果如下。

N-1前负荷阻抗矩阵及负荷发电机阻抗矩阵分别为

由式（22）得修正矩阵ZLL1为

由式（24）得YLG1为

再根据式（8）及式（24）、（25）得ZLG为

由式（26）得修正矩阵ZLG1为

由式（28）、（29）得YLL1、YLG1为

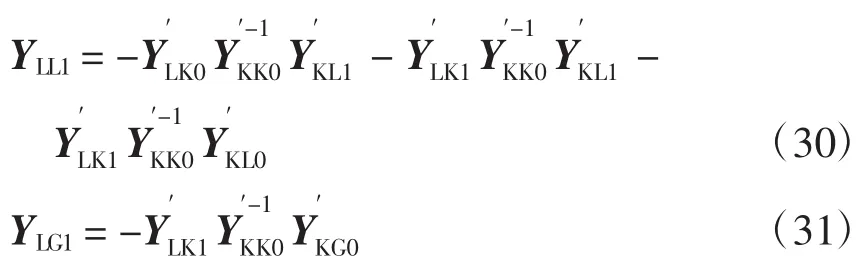
将式（28）～（31）代入式（7）、（8）有

由式（32）及（33）得修正矩阵ZLL1、ZLG1分别为

由式（36）得

将式（36）代入式（7）、（8）分别得

由式（38）及（39）知，负荷阻抗矩阵不变ZLL1= 0，则ZLG1为

（4）负荷节点间支路开断，由式（6）知YLL1=Y再由式（7）得

由式（41）得ZLL1为

再将式（41）代入式（8）得ZLG为

由式（43）得ZLG1为

由式（46）得ZLG1为

式（23）～（48）给出了网络中出现各种断线类型后负荷阻抗矩阵的修正矩阵ZLL1和负荷-发电机阻抗矩阵的修正矩阵ZLG1的求解方程，需要指出的是，在上述计算过程中的绝大部分修正矩阵是稀疏矩阵，可采用稀疏矩阵的相关计算方法来提高计算的速度。当系统在线进行N-1校验时，根据不同支路开断信息，判断支路开断类型，计算对应的负荷阻抗矩阵的修正矩阵ZLL1和负荷-发电机阻抗矩阵的修正矩阵ZLG1；然后根据得到的修正矩阵ZLL1、ZLG1更新ZLL、ZLG；假定支路开断前后，系统各发电机端电压和有功出力、负荷消耗的有功、无功保持不变，依据式（17）便可快速计算各节点的电压稳定裕度，从而确定在不同N-1故障下系统的电压稳定裕度。

3 算例分析

为验证所提出的电压稳定裕度估计方法的有效性和合理性，本文分别在New England 39、IEEE 300测试系统上进行了大量的仿真验证，限于篇幅，本文仅以部分算例为例给予阐述，算例的其他相关结论类似，不再赘述。在仿真验证过程中，本文均采用连续潮流CPF（continuous power flow）的结果来验证所提方法，负荷按恒功率因数增长，发电机出力按照各发电机有功剩余容量的比例分配增加的有功负荷。

3.1 New England 39系统算例

图3从基态出发按确定的负荷增长方式及发电机出力方式，计算得到的New England 39系统的电压稳定裕度曲线，图中横坐标λinc为系统的负荷增长因子；纵坐标λmarg为系统的电压稳定裕度因子；电压稳定裕度VSM（voltage stability margin）为采用本文方法计算得到的电压稳定裕度曲线；CPF为采用连续潮流计算得到的电压稳定裕度曲线。图中CPF电压稳定裕度的计算方法为λmarg= λcr-λinc，因此其电压稳定裕度曲线为线性的，而VSM的电压稳定裕度曲线随着负荷增长因子的增加呈非线性单调递减的特点，由式（25）可知，理论上在系统网络结构保持不变的情况下YLLii不变，发电机未到达无功输出极限时U2eqi不变，全网负荷按等功率因数增加时φeqLLi也保持不变，VSM值随负荷稳定因子的增长应线性变化，但实际计算过程中只有YLLii保持不变，而U2eqi和φeqLLi随着节点电压相位的变化均会发生变化，因而出现如图3所示的结果。同时由图1可知，VSM计算得到的电压稳定裕度值均小于CPF计算得到的电压稳定裕度值，在基态λinc=0下采用本文方法计算得到电压稳定裕度值λmarg为2.112 4，而采用连续潮流计算得到的电压稳定裕度值λmarg为2.213 8，随着全网负荷的增长，采用VSM与CPF计算得到电压稳定裕度都不断减小，当λinc=2.066 4时，采用VSM计算到的电压稳定裕度值λmarg=0，而CPF计算得到的电压稳定裕度值λmarg=0.146 5，即VSM计算得到的电压稳定裕度具有一定的保守性。

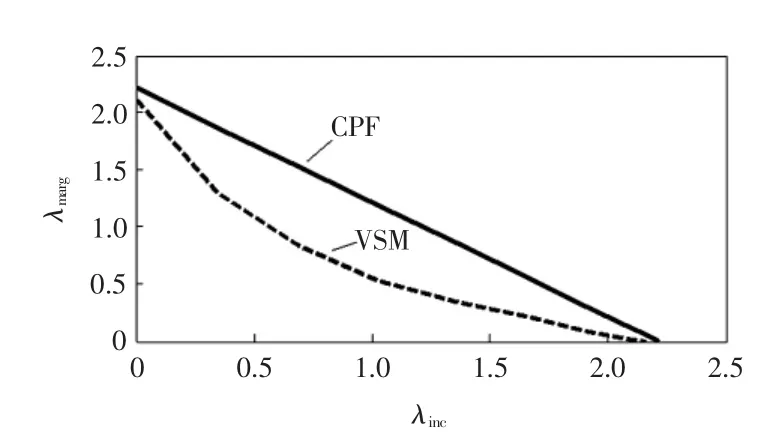
图1 New England 39系统的电压稳定裕度曲线Fig.1 Voltage stability margin curves of New England 39

图2给出了采用本文VSM计算得到的New England 39节点测试系统部分负荷节点的电压稳定裕度曲线，由图可知，在New England 39测试系统中，随着负荷增长Bus8的电压稳定裕度曲线一直位于曲线簇的最底层，且其电压稳定裕度较其他节点最先到达0，因此可判断在采用VSM计算New England 39测试系统电压稳定裕度过程中，母线8为按该负荷增长方式系统最弱电压节点，即Bus8的电压稳定裕度曲线为系统的电压稳定裕度曲线，即图1中的VSM曲线对应于图2中的Bus8的电压稳定裕度曲线。为进一步验证上述结论，表1给出了部分负荷节点在计算过程中的电压稳定裕度值，由表1结果可知，随着系统负荷增长因子的增加，节点8的电压稳定裕度值一直小于其他负荷节点的电压稳定裕度值，且其电压稳定裕度值先于其他节点到0，图2和表1的结果一致说明母线8为系统电压最弱节点，而上述结果与采用CPF计算得到的最弱电压节点结果一致。

图2 New England 39系统节点的电压稳定裕度曲线Fig.2 Voltage stability margin curves of Node for New England 39

为进一步验证本文提出的考虑系统支路开断时的电压稳定裕度修正模型，结合New England 39测试系统的网络拓扑图，分别设置了17种断线故障，并采用修正模型估算系统支路开断模式下的电压稳定裕度，估算结果如表2所示。表中02—03、04—14、04—05、05—08、17—18、21—22的支路开断为联络节点与负荷节点间的支路开断模式；05—06、06—11、12—13为联络节点间的支路开断模式；03—18、07—08、16—24、23—24、25—26、26—28、26—29、28—29为负荷节点间的支路开断模式，其他三种支路开断模式受New England 39测试系统的网络拓扑结构限制，未能测试。对比分析表2结果可知：采用本文方法在系统支路开断模式下计算得到的系统电压稳定裕度值均具有较好的预测结果，未出现过估计的情况。

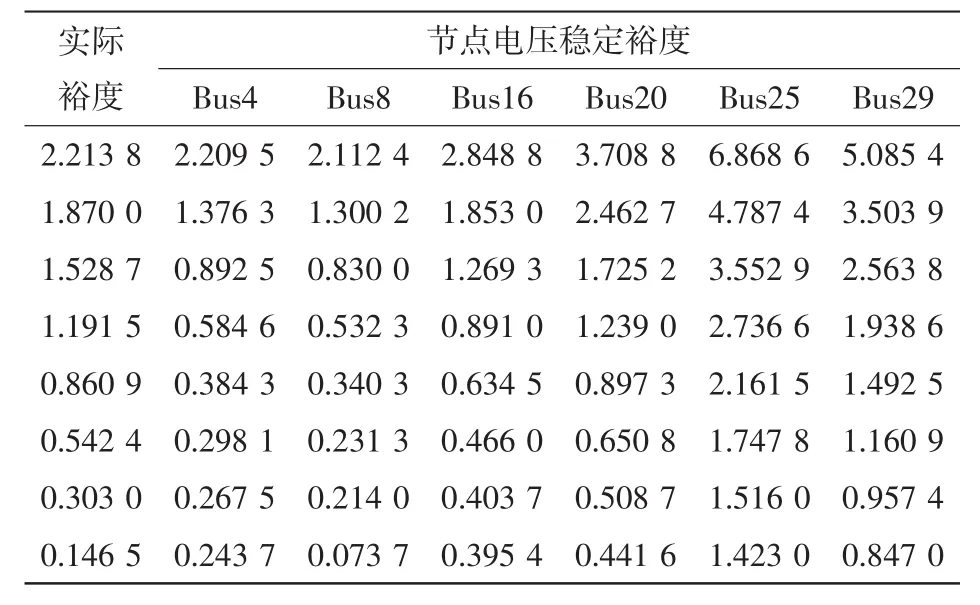
表1 New England 39系统节点电压稳定裕度Tab.1 Voltage stability margin for New England 39

表2 New England 39系统支路开断时的电压稳定裕度Tab.2 Voltage stability margin of New England 39 with branch outage

3.2 IEEE 300系统算例

上节New England 39测试系统算例验证了本文所提方法的有效性和正确性，本节进一步通过在IEEE 300节点测试系统讨论所提到方法在大规模电力系统中应用的可行性，结果如图3～4及表3～4所示。图3给出了采用本文方法和CPF方法计算得到的系统电压稳定裕度曲线，图中VSM的电压稳定裕度曲线特点与New England 39节点测试系统VSM曲线类似，均位于CPF电压稳定裕度曲线以下，基态时采用本文方法计算得到电压稳定裕度值λmarg为0.980 5，而采用连续潮流计算得到的电压稳定裕度值λmarg为1.428 3，随着全网负荷的增长，采用VSM与CPF计算得到电压稳定裕度都不断减小，当VSM计算到的电压稳定裕度值时λmarg=0.003 1，CPF计算得到的电压稳定裕度值λmarg=0.206 2，对比图3、表1可知，采用本文方法计算得到的IEEE300节点测试系统的电压稳定裕度误差较England 39节点测试系统大，主要因为，在IEEE 300节点测试系统中存在的负荷与发电机为同一母线的较England 39节点测试系统多，通常在处理这种共线节点时，在发电机无功未失去调节能力时将负荷发电机节点视为PV节点来处理，这样就没有考虑共线节点中负荷对节点电压稳定裕度的贡献，计算误差较大，而实际电力系统中负荷一般都经过变压器接入高压母线，极少存在负荷与发电机直接为同一母线的情况，因此在实际应用时，这部分误差是可以避免的。

图3 IEEE 300系统的电压稳定裕度曲线Fig.3 Voltage stability margin curves of IEEE 300

图4给出了采用本文VSM方法计算IEEE300节点测试系统得到的电压稳定裕度曲线簇，由图可知，随着全网负荷的增加，母线192的电压稳定裕度曲线一直处于曲线簇的底部，且先于其他节点的电压稳定裕度曲线到达横轴，对比表3的部分负荷节点电压稳定裕度数值计算结果可知，母线192的电压稳定裕度值最先为0，因而可以确定母线192为系统的电压最弱节点，图3中的系统的电压稳定裕度也应为图4中母线192的电压稳定曲线，上述结果与采用CPF追踪系统PV曲线得到的结果一致。

图4 IEEE 300系统节点的电压稳定裕度曲线Fig.4 Voltage stability margin curves of Node for IEEE 300

表3 IEEE 300系统节点电压稳定裕度Tab.3 Voltage stability margin of node for IEEE 300

表4 IEEE 300系统支路开断时的系统电压稳定裕度Tab.4 Voltage stability margin of IEEE 300 with branch outage

为进一步验证本文所提出的考虑系统支路开断时电压稳定裕度修正模型在多节点系统中适应性，结合IEEE300测试系统的网络拓扑结构，设置了19种支路断线故障，其中157—159、228—231、204—205为负荷节点间的支路开断模式；145—146、138—188、190—231为负荷节点与发电机节点间的支路开断模式；117—159、224—226、193—205、44—45、211—212为负荷节点与联络节点间的支路开断模式；194—219、195—219为联络节点间的支路开断模式；143—149、146—147、176—177、152—153、220—221为发电机节点间的支路开断模式；132—170为发电机与联络节点间支路开断模式。上述19种支路断线故障包含了本文所提的6种支路开断模式，限于篇幅文中未给出各支路开断类型的修正矩阵ZLL1、ZLG1，仅给出采用修正模型估算系统在各种支路开断模式下的电压稳定裕度，估计结果如表4所示。对比分析表4结果可知，本文方法均较好地估算出了系统在各种断线模式下的电压稳定裕度，其计算结果均在可以接受的范围内，未出现过估计的情况，可为系统在断线故障时系统电压稳定性判别提供参考信息。

从New England 39、IEEE 300节点测试系统的仿真结果可以看出，本文的电压稳定裕度计算模型均准确识别出系统的电压薄弱节点，给出可接受的电压稳定裕度信息，所提出的考虑支路开断故障的电压稳定裕度修正模型均较好地预测出支路开断后系统的电压稳定裕度，计算精度能满足电压稳定在线监控的需要。

4 结语

本文基于电力系统局部量测信息提出一种在线快速估计系统N-1时的电压稳定裕度新方法，首先给出基于局部量测信息的电力系统电压稳定裕度求解模型；在此基础上，推导并给出利用系统支路断线故障前信息快速估计N-1下的系统电压稳定裕度修正模型；最后对所提方法进行了仿真验证。

New England 39节点测试系统算例验证了本文所提N-1时电压稳定裕度模型的有效性和正确性；进一步通过IEEE300节点测试系统算例验证了所提出求解模型及修正模型在大规模电力系统中应用的可行性。本文方法利用系统当前信息即可快速估算出系统的电压稳定裕度、准确确定系统电压薄弱节点，计算速度快、精度较高，且可给出丰富的电压稳定裕度信息，并可在系统支路开断模式下快速预测各负荷节点及系统的电压稳定裕度信息，有利于调度/运行人员全面掌握系统运行的电压状态。

[1]Pourbeik P，Kundur P S，Taylor C W．The anatomy of a power grid blackout[J]．IEEE Power&Energy Magazine，2006，4（5）：22-29．

[2]Kunder P，Paserba J，Ajjarapu V，et al.Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions[J]．IEEE Trans on Power Systems，2004，19（3）：1387-1401．

[3]Claudio Canizares.Voltage Stability Assessment：Concepts，Practices and Tools[R].Waterloo：School of Electrical and Computer Engineering，University of Waterloo，2002．

[4]李国庆，李小军，彭晓洁（Li Guoqing，Li Xiaojun，Peng Xiaojie）．计及发电报价等影响因素的静态电压稳定分析（Static voltage stability analysis considering influencing factors such as generation bidding）[J]．中国电机工程学报（Proceedings of the CSEE），2008，28（22）：35-40．

[5]贾宏杰，孙晓彦，张沛（Jia Hongjie，Sun Xiaoyan，Zhang Pei）．基于L指标的电压稳定约束下的最优潮流（Optimal power flow with voltage stability constraint based on L index）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（1）：34-38，111．

[6]陈厚合，李国庆，姜涛（Chen Houhe，Li Guoqing，Jiang Tao）．计及静态电压稳定约束的交直流系统可用输电能力（Available transfer capability of hybrid AC/DC power system considering constraint of static voltage stability）[J]．电网技术（Power System Technology），2012，36（2）：75-81．

[7] 魏炜，贾宏杰，王成山（Wei Wei，Jia Hongjie，Wang Chengshan）．PSVSR：一种实用的静态电压安全性评估工具（PSVSR：A practical tool for power system static voltage security assessment）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（3）：25-30．

[8]苗伟威，贾宏杰，董泽寅（Miao Weiwei，Jia Hongjie，Dong Zeyin）．基于有功负荷注入空间静态电压稳定域的最小切负荷算法（A minimum load shedding calculation algorithm based on static voltage stability region in active load power injection space）[J]．中国电机工程学报（Proceedings of the CSEE），2012，32（16）：44-52．

[9]林舜江，李欣然，刘杨华（Lin Shunjiang，Li Xinran，Liu Yanghua）．电力系统电压稳定性及负荷对其影响研究现状（Present investigation of voltage stability and composite load’s influence on it）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（1）：66-74．

[10]吴政球，黄庆云，潘纪良，等（Wu Zhengqiu，Huang Qingyun，Pan Jiliang，et al）．N-1网络电压及灵敏度快速算法（Rapid algorithm of voltage and voltage sensitivity for N-1 power system）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（1）：118-123．

[11]王秀婕，李华强，李波（Wang Xiujie，Li Huaqiang，Li Bo）．基于内点法的交直流系统电压稳定性评估（Voltage stability assessment for AC/DC power systems based on interior point method）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（6）：72-77．

[12]Terzija V，Valverde G，Cai Deyu，et al．Wide-area monitoring protection，and control of future electric power networks[J]．Proceedings of the IEEE，2011，99（1）：80-93．

[13]Karlsson Daniel，Hemmingsson Morten，Lindahl Sture．Wide area system monitoring and control[J].IEEE Power and Energy Magazine，2004，2（5）：68-76．

[14]Leonardi B，Ajjarapu V．Development of multilinear regression models for online voltage stability margin estimation[J]．IEEE Trans on Power Systems，2011，26（1）：374-383．

[15]Taylor C W，Erickson D C，Martin K E，et al．WAC-widearea stability and voltage control system：R&D and online demonstration [J]．Proceedings of IEEE，2005，93（5）：892-906．

[16]李国庆，姜涛，徐秋蒙，等（Li Guoqing，Jiang Tao，Xu Qiumeng，et al）．基于局部电压稳定指标的裕度灵敏度分析及应用（Sensitivity analysis based on local voltage stability margin and its application）[J]．电力自动化设备（Electric Power Automation Equipment），2012，32（4）：1-5，30．

[17]姜涛，陈厚合，李国庆（Jiang Tao，Chen Houhe，Li Guoqing）．基于局部电压稳定指标的电压/无功分区调节方法（A new algorithm for partitioned regulation of voltage and reactive power in power system utilizing local voltage stability index）[J]．电网技术（Power System Technology），2012，36（7）：207-213．

[18]牟晓明，李志民（Mou Xiaoming，Li Zhimin）．电压薄弱节点的在线识别与控制方法（An analytical method for online identification and control of voltage weak buses）[J]．电网技术（Power System Technology），2012，36（8）：163-168．

[19]Abdelkader S M，Morrow D J．Online tracking of Thevenin equivalent parameters using PMU measurements[J]．IEEE Trans on Power Systems，2012，27（2）：975-983．

[20]姜涛，李国庆，贾宏杰，等（Jiang Tao，Li Guoqing，Jia Hongjie，et al）．电压稳定在线监控的简化L指标及其灵敏度分析方法（Simplified L-index and its sensitivity analysis method for on-line monitoring of voltage stability control）[J]．电力系统自动化（Automation of Electric Power Systems），2012，36（21）：13-18．

[21]贾宏杰（Jia Hongjie）．电力系统小扰动稳定域的研究（Studies on Small Signal Stability Region of Electrical Power Systems）[D].天津：天津大学电气与自动化工程学院（Tianjin：School of Electrical Engineering and Automation of Tianjin University），2001．

Voltage Stability Margin Estimation with N-1 Contingency

ZHANG Ji-nan1，JIANG Tao1，JIA Hong-jie1，ZHAO Jin-li1，QIU Lu-lu1，KONG Xiang-yu1，LI Peng2
（1.Key Laboratory of Smart Grid of Ministry of Education，Tianjin University，Tianjin 300072，China；2.China Southern Grid Dispatch and Control Center，Guangzhou 510623，China）

This paper focuses on the online voltage stability margin estimation with N-1 contingency.A model of voltage stability margin estimation is proposed for the large-scale power system.Based on the model，a modified model is developed to predict the voltage stability margin for N-1 contingency，and the proposed method is applied to two benchmark systems.The appeal of the approach has inherently physical intuition and fast calculation performance.It can accurately identify the weakest node and provide more voltage stability margin information using the current status of power system.The New England 39，IEEE 300 test cases are used to numerically validate the viability and effectiveness of the proposed method.

voltage stability；voltage stability margin；N-1 contingency；local measurement information

TM769；TM73

A

1003-8930（2013）06-0001-08

张继楠（1989—），男，硕士研究生，研究方向为电力系统安全性与稳定性。Email：jinan_zhang@yeah.net

2013-04-13；

2013-05-31

国家重点基础研究发展计划（973计划）项目（2009CB219701；2010CB234608）；国家自然科学基金项目（51277128）；天津市科技发展计划项目（09JCZDJC25000-2012）；国家电网公司大电网重大专项资助项目（SGCC-MPLG028-2012）

姜 涛（1983—），男，通信作者，博士研究生，研究方向为电力系统安全性与稳定性、新能源集成。Email：electricpowersys@163.com

贾宏杰（1973—），男，博士，教授，博士生导师，研究方向为电力系统安全性与稳定性、配电系统规划、智能电网。E－mail：hjjia@tju.edu.cn