直驱风电系统双PWM变流器非线性控制策略

马先芹，王久和

（北京信息科技大学自动化学院 北京 100192）

直驱风电系统双PWM变流器非线性控制策略

马先芹，王久和

（北京信息科技大学自动化学院 北京 100192）

在直驱风电系统中，为了提高变流器的性能，该文提出了外环采用PI控制，内环采用无源控制的混合控制策略。根据主电路拓扑结构分别建立了在dq坐标系下的欧格-拉格朗日EL（Euler-Lagrange）模型和端口受控耗散哈密顿PCHD（port control Hamiltonian with dissipation）模型。基于EL模型，采用了注入阻尼的方法，得到无源控制律；而基于PCHD模型，采用能量成形的方法，利用IDA-PBC（injecting dampingpassivity-based contro）控制算法设计无源控制器。仿真结果表明机侧变流器能够实现对转速的控制；网侧变流器实现直流电压跟踪控制、单位功率因数并网。实验验证了所提控制策略的可行性。

永磁同步电机；双脉冲宽度调制（PWM）变流器；无源控制；阻尼注入；端口受控耗散哈密顿

风能是最重要的清洁和可再生能源之一，资源丰富。直驱型是一种新型的风电系统也开始逐渐受到关注，它通过功率变换电路后并入电网，省去了齿轮箱，具有结构简单、发电效率及运行可靠性高、电网低压运行等优点[1-2]。

在PWM变流器设计中，常用的控制策略有功率控制[3]、反馈线性化控制[4-5]、基于无源理论的控制、PI控制。目前基于同步旋转坐标系下的电压、电流双闭环控制策略被众多学者采用[6-7]，但由于只采用PI控制器，调试难度大、结构复杂等不足。对此，本文提出了以无源控制为主、PI控制为辅的混合控制，分别建立了基于EL和基于PCHD的数学模型，利用无源控制理论[8-9]设计无源控制器，使变流器具有良好的性能。实验验证了所提控制策略的可行性。

1 双PWM变流器拓扑结构及建模

1.1 双PWM变流器拓扑结构

直驱风电系统双PWM变流器拓扑结构如图1所示。为建立其数学模型，假设：①电源为三相对称正弦电压；②滤波电感是线性的，且不考虑饱和；③开关为理想开关，无导通关断延时，无损耗。

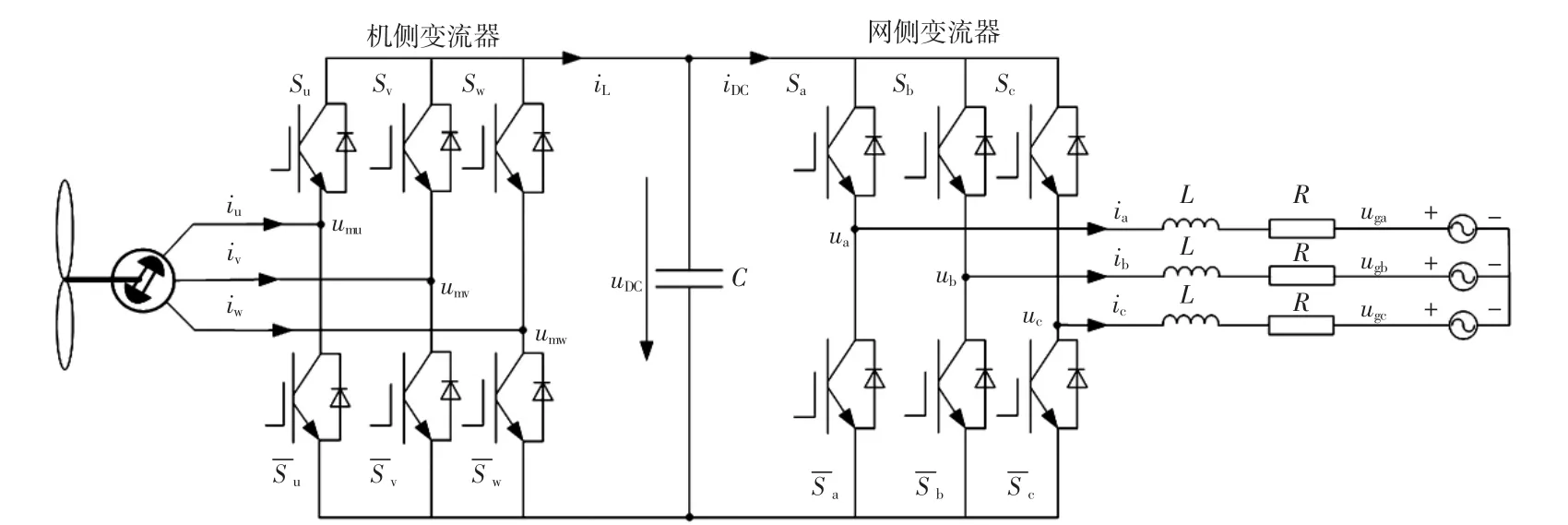
图1直驱风电系统双PWM变流器拓扑结构Fig.1 Topology of dual-PWM converter with direct-drive wind power system

1.2 机侧变流器的数学模型

机侧变流器被控对象为多级低速永磁同步发电机，通常采用转子磁场定向的矢量控制技术，将d轴定位于转子磁链上，可得永磁同步电机在同步旋转dq坐标系下的数学模型为

式中：isd、isq和usd、usq分别为定子电流和电压在dq轴分量；Lsd、Lsq分别为dq轴同步电感分量且Lsd= Lsq=L；ωr为电机的机械角速度；p为极对数；Rs为定子电阻；ψr为转子磁链；Tm1为机械转矩；J为系统的转动惯量；D为与转速成正比的转矩阻尼系数。

将式（1）化成EL方程的标准形式，可得

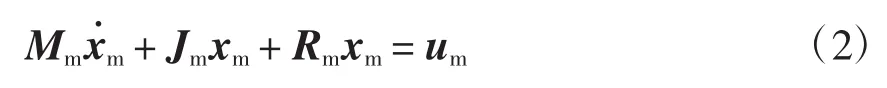
式中：Mm为正定的对角阵；Jm为反对称矩阵，Jm= -JmT，反映系统内部的互联结构；Rm为对称正定矩阵，反映系统的耗散特性；xm为相应变量的矩阵；um为系统与外部的能量交换。其中，下标m表示与机侧变流器有关的参数。各矩阵具体表达式为

1.3 网侧变流器的数学模型

在三相对称电源电压情况下，网侧变流器在三相abc坐标系下的数学模型为

将变流器在三相abc坐标系下的系统等量变换到两相同步旋转坐标系统中，其等量变换的矩阵为

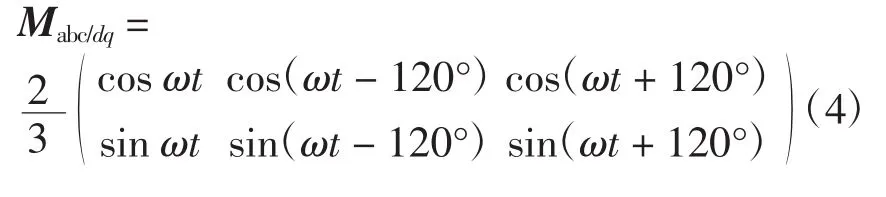
于是可得在同步旋转dq坐标系下网侧变流器的数学模型为

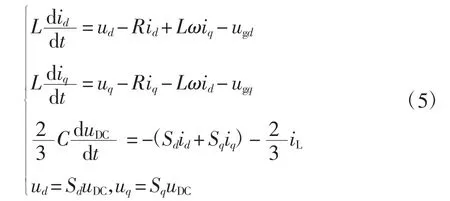
式中：Sd、Sq分别为开关函数在dq轴上的分量；ugd、ugq网侧变流器三相交流电源在dq轴上的分量。其中iL相当于整流器的输出电流。

令x1=Lid，x2=Liq，x3=CuDC，系统的总能量为

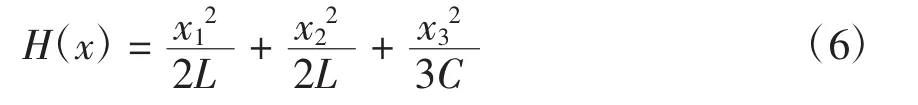
将式（5）变为

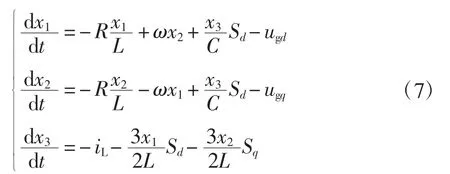
将式（7）写成标准的PCHD形式

式中：J为反对称矩阵，即J=-JT，反映系统内部的互联结构；R为对称正定矩阵，反映系统的耗散特性；g反映了系统的端口特性；u为系统与外部的能量交换。各矩阵具体表达式为

2 控制器设计

2.1 机侧变流器混合控制器设计

2.1.1 转速外环的设计

根据被控对象可确定闭环系统的期望平衡点为

其中：ωr*是系统给定转速；isd*、isq*分别为定子期望电流在dq轴上的分量。对此本文采用电流isd*=0的矢量控制，isq*为PI控制器的输出，其传递函数为

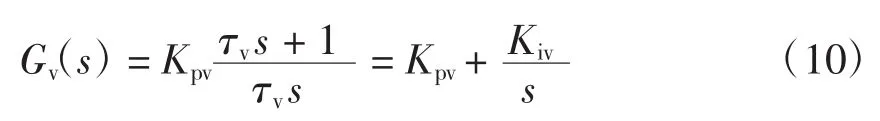
式中，Gv（s）、τv、Kpv、Kiv分别代表传递函数，采样时间常数，PI控制器的比例和积分系数。于是可以按照典型II型系统来选择Kpv和Kiv。

2.1.2 无源控制器设计

式中，xem和分别代表变量的误差和对应变量的期望值。

取误差能量函数

为使系统快速收敛到期望点，使误差能量函数快速变零，需要注入阻尼，加快系统耗散。注入阻尼耗散项为

式中：Ri为系统的总耗散项；Ra为系统具体的注入阻尼，则式（11）可变成

选取控制律为

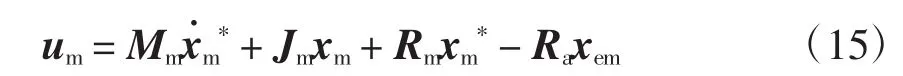
可使

由式（15）可以得到具体的无源控制律为

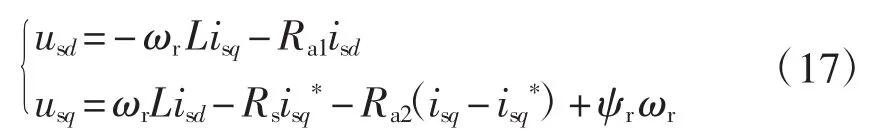
式中，Ra1、Ra2、Rs分别代表系统的注入阻尼和永磁同步电机的定子电阻。

将式（17）带入式（2）可得

由式（18）可以看出，所得到的控制律可以实现电流解耦控制。

2.2 网侧变流器混合控制器设计

2.2.1 电压外环的设计

考虑到网侧变流器直流侧电压uDC的动态性，本文电压外环采用PI控制器，使uDC快速收敛并稳定于直流侧电压给定值uDC*，其设计方法同转速外环的设计。

2.2.2 IDA-PBC设计

IDA-PBC最终目标是找到静态状态反馈控制律u=β（x）使闭环系统具有的结构形式为

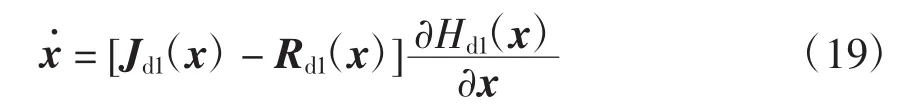
式中：Hd1（x）为闭环系统新的能量函数，在期望平衡点x*有严格局部最小值；Jd1（x）=-Jd1T（x）为新的互联矩阵；Rd1（x）=Rd1T（x）≥0为新的阻尼矩阵。

对于给定的J（x，u），R（x），g（x，u），H（x）和期望稳定的平衡点x*∈Rn。假设能找到β（x）、Ja1（x）、Ra1（x）和一个矢量函数K（x），满足

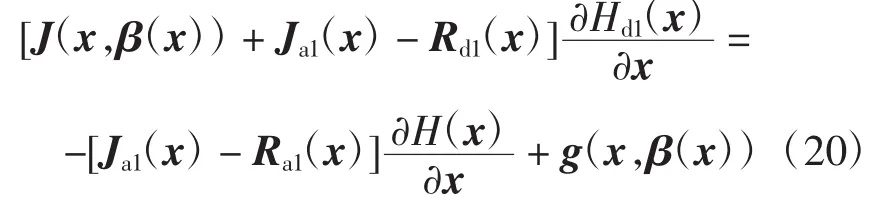
式中：J（x，β（x））、g（x，β（x））分别与式（8）中的J、g意义相同；H（x）为能量函数；Ja1（x）、Ra1（x）分别为系统注入的反对称矩阵和系统注入阻尼。

（1）结构守恒：

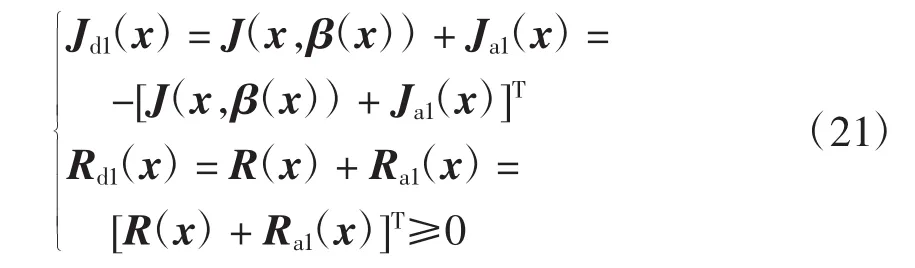
（2）可积性：K（x）是标量函数的梯度

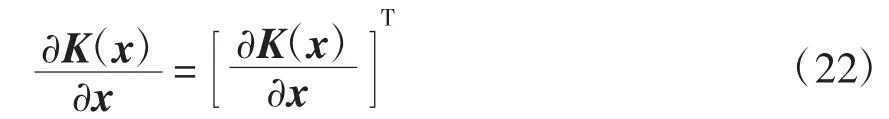
（3）平衡点指定：在期望平衡点x*处，K（x）满足

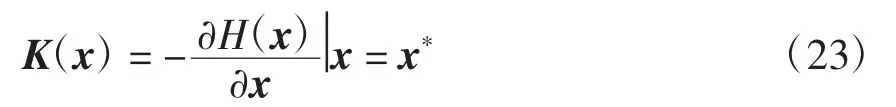
（4）Lyapunov稳定性：在x*处，K（x）的雅克比矩阵满足

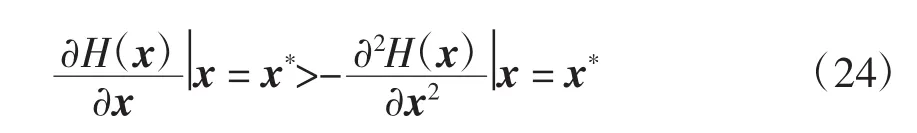
式（24）是Hd1（x）在x*处存在最小值的必要条件。

能量函数Hd1（x）和Ha1（x）为

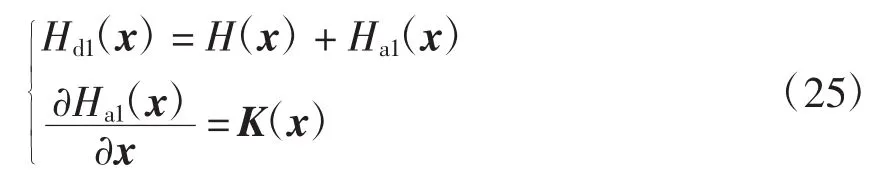
式中：Hd1（x）为新的能量函数；Ha1（x）为一待定函数，它表示通过控制注入系统的能量。

利用式（20）可得

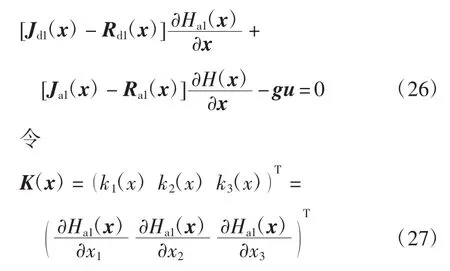
取Ja1（x）=0，Ra1（x）=0，由式（26）可得

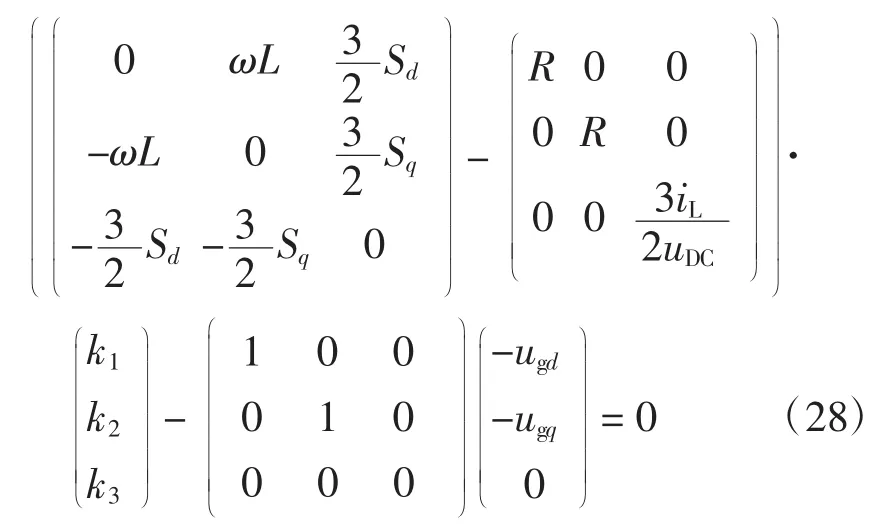
由式（28）可得

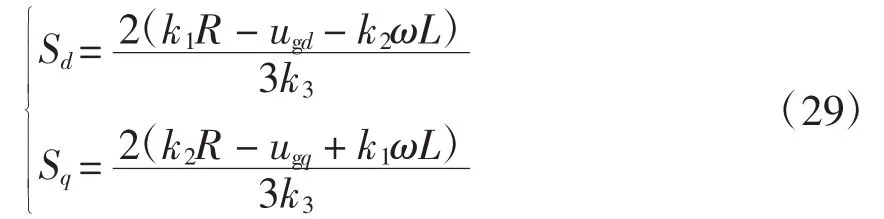
为了简化控制器的设计，设k1（x）、k2（x）、k3（x）均为x3的函数，根据可积性有

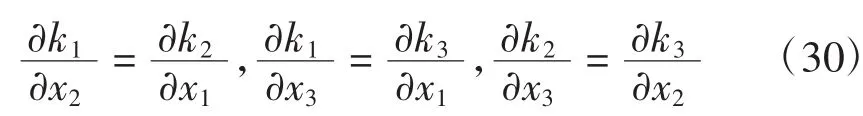
可得k1=A1，k2=A2。

为实现在x*处Hd1（x）有极值，根据= 0，并考虑到，可得

式（31）满足式（23），由式（31）可确定Ha1（x*）为

则有Hd1（x*）=H（x）+Ha1（x*）。由计算可得

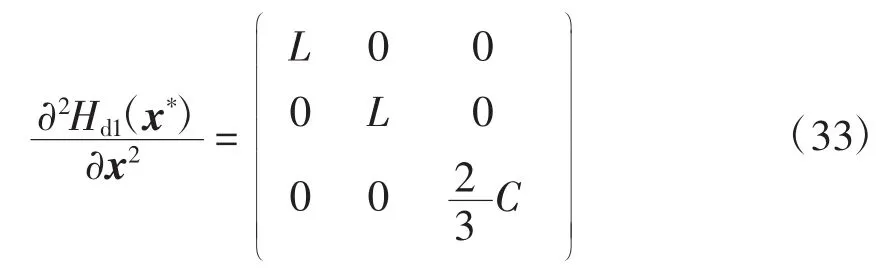
将式（31）带入式（29）中，可得网侧变流器的开关函数为

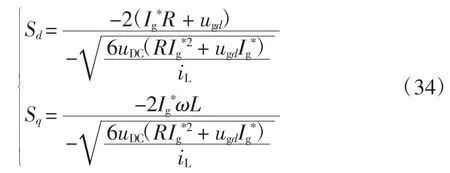
综合以上的控制策略，可得基于无源混合控制策略的直驱风电系统结构框图如图2所示。

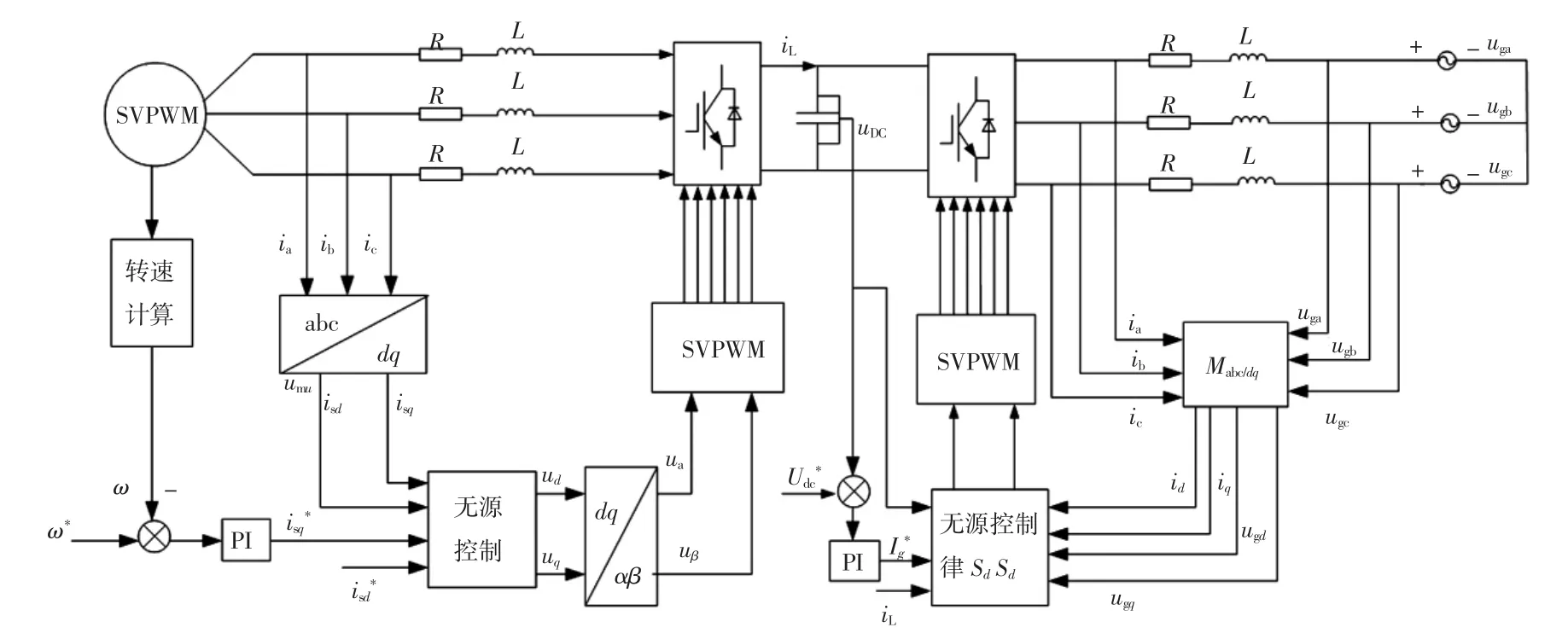
图2 基于无源混合控制的直驱风电系统结构框图Fig.2 Structure diagram of direct-drive wind power system based on passive hybrid control

3 实验研究

3.1 仿真研究

用Matlab/Simulink软件对系统进行仿真，机侧变流器中给定转速ωr*=1 000 r/min，仿真用PMSM参数为：Rs=2.875 Ω，Lsd=Lsq=L=8.5 mH，ψf=0.175 Wb，J=1×10-3kg·m2，D=0，p=4，K=0，Tm=3 N·m；当采用混合控制时，转速环中的参数kp=0.06，ki=0.57，网侧变流器中电压外环的参数kp=0.1，ki=1.77；当采用经典PI控制时，转速环中的PI参数为kp=5，ki=4；电流内环PI参数为kp= 10，ki=2.6；网侧变流器电压外环PI参数为kp= 3.3，ki=2.3；直流电压期望值设为650 V，电抗值为15 mH，电抗器内阻和线路电阻之和为0.3 Ω，电容器为1 000 μF，注入阻尼Ra=100 Ω，电网电源交流幅值为311 V。

机侧变流器仿真结果如图3～图6所示。由图3可以看出三相电流是波形稳定的正弦波，但采用混合控制时性能更好；变流器轴电流仿真波形如图4所示，实现了轴的解耦控制；转速仿真波形如图5所示，可得采用混合控制具有响应速度更快，稳定性更好等优点。

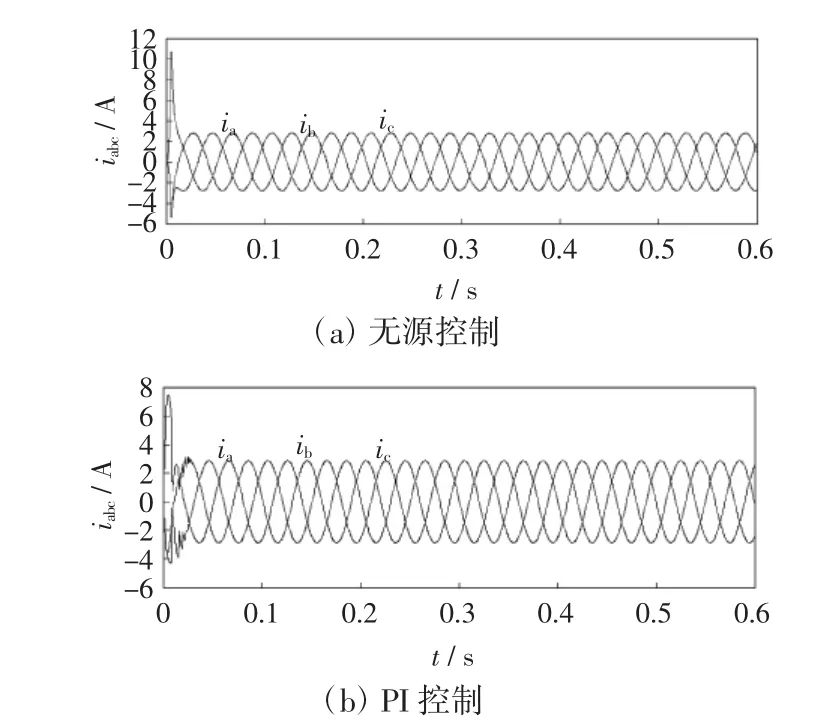
图3 机侧变流器三相电流仿真波形Fig.3 Three-phase current simulation waveform of machine-side converter

网侧变流器仿真结果如图6～图8所示，由图6可知电压外环能很快的跟踪给定电压值，结果表明采用无源混合控制具有动态性能好、波动性小，稳定性好、基本无超调等优点。图7表明采用混合控制时可实现电压电流同步，电流正弦化，并且基本达到单位功率因数并网；THD分析如图8所示，满足THD＜5%要求，可看出采用无源混合控制的THD会更小。

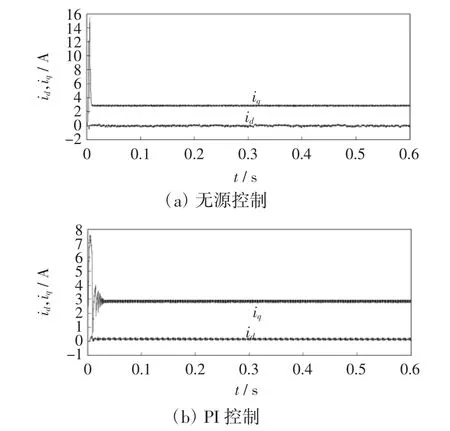
图4 机侧变流器轴电流仿真波形Fig.4 Shaft current simulation waveforms of machine-side converter

图5 转速仿真波形Fig.5 Speed simulation waveform

图6 网侧变流器电压仿真波形Fig.6 Voltage simulation waveform of grid-side converter

图7 网侧变流器a相电压与a相电流仿真波形Fig.7 A phase voltage and current simulation waveforms of grid-side converter

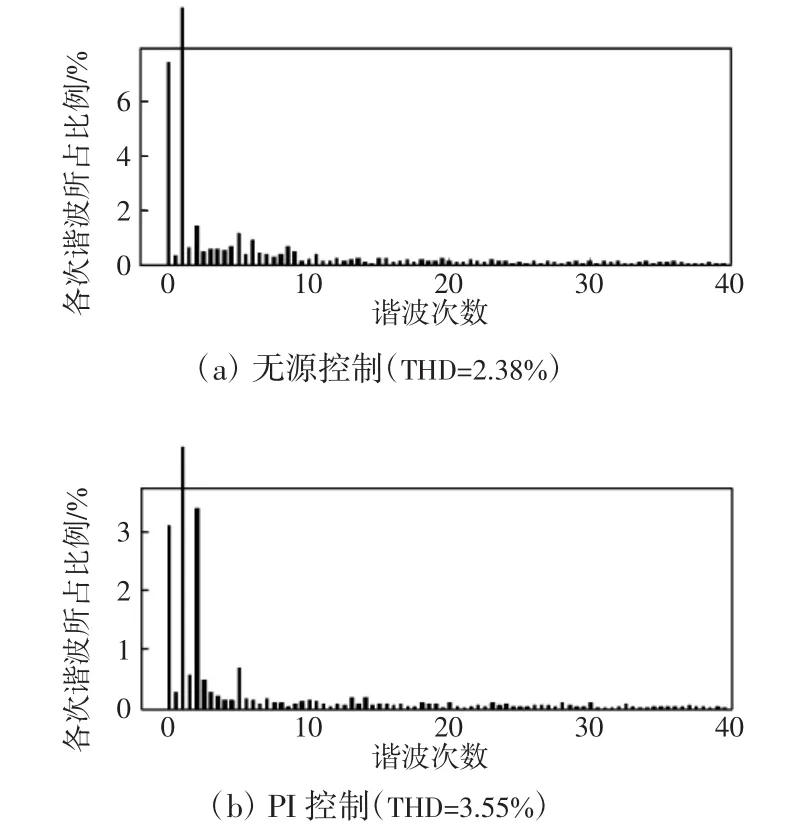
图8 电流总谐波畸变率Fig.8 Total harmonic distortion of current

3.2 实验研究

为验证所提控制策略的可行性，本文进行了局部并网研究，将永磁同步电机和机侧变流器等效为一个电压源。其样机实验平台如图9所示。将直流电压设置为380V，考虑到响应的快速性，在实验中注入阻尼，其Ra=30 Ω。测量部分采用FLUKE电能质量分析仪和Tektronix TP2014 100 M数字隔离示波器进行测量。

图9 硬件实验平台Fig.9 Hardware experimental platform

由FLUKE测量的功率、功率因数、电流谐波畸变率情况分别如图10～图12所示，由示波器测量的相电压和相电流的波形如图13所示，结果表明功率因数可达0.99，电流谐波总畸变率的平均值为2.8%。

图10 功率和功率因数Fig.10 Power and power factor

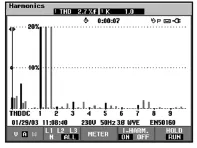
图11 交流侧电流谐波含量柱形图Fig.11 Bar chart of AC current harmonic content

图12 交流侧电流各次谐波分布Fig.12 Harmonic distribution of AC current

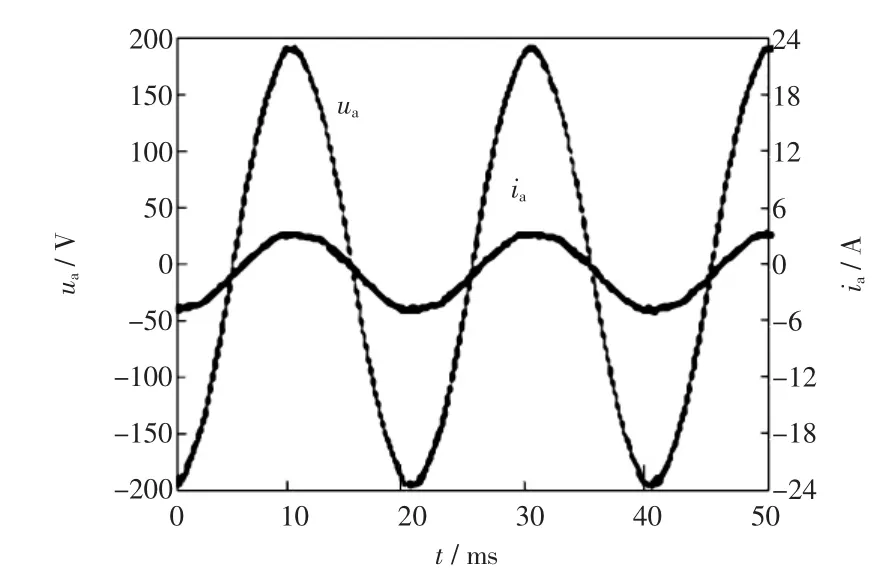
图13 电压电流波形Fig.13 Waveforms of voltage and current

4 结语

本文针对直驱风电系统提出了一种无源混合控制策略。仿真结果表明机侧变流器能够实现对永磁同步电机的转速控制；网侧PWM逆变器能够实现直流侧电压能够快速跟踪期望值，单位功率因数并网。实验验证了所提控制策略的可行性。

[1]李建林，许洪华.风力发电中的电力电子变流技术[M].北京：机械工业出版社，2008.

[2]姚骏，廖勇，李辉，等（Yao Jun，Liao Yong，Li Hui，et al）.直驱永磁同步风力发电机单位功率因数控制（Unity power factor control of a direct-driven permanent magnet synchronous wind-power generator）[J].电机与控制学报（Electric Machines and Control），2010，14（6）：13-20.

[3]李明水（Li Mingshui）.双PWM变换器负载功率前馈直接功率控制（Dual PWM Converter Load Power Feed-Forward Direct Power Control）[D].天津：天津大学电气与自动化工程学院（Tianjin：School of Electrical Engineering and Automation，Tianjin University），2012.

[4]邓卫华，张波，丘东元，等（Deng Weihua，Zhang Bo，Qiu Dongyuan，et al）.三相电压型PWM整流器状态反馈精确线性化解耦控制研究（The research of decoupled state variable feedback linearization control method of three-phase voltage source PWM rectifier）[J].中国电机工程学报（Proceedings of the CSEE），2005，25（7）：97-103.

[5]张平化，杨贵杰，李铁才（Zhang Pinghua，Yang Guijie，Li Tiecai）.三相PWM整流器的反馈线性化直接电压控制（Direct voltage control of three-phase PWM rectifier based on feedback linearization）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（18）：39-46.

[6]李建林，高志刚，胡书举，等（Li Jianlin，Gao Zhigang，Hu Shuju，et al）．并联背靠背PWM变流器在直驱型风力发电系统的应用（Application of parallel back-to-back PWM converter on the direct-drive wind power system）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（5）：59-62．

[7]李燕，梁英（Li Yan，Liang Ying）.永磁直驱风电系统电压源型变流技术（Voltage source converter technology in permanent magnet directly driven wind power system）[J].电力系及其自动化学报（Proceedings of CSU-EPSA），2010，22（1）：65-70.

[8]王久和.无源控制理论及其应用[M].北京：电子工业出版社，2010.

[9]王久和.电压型PWM整流器的非线性控制[M].北京：机械工业出版社，2008.

Nonlinear Control Strategy of Dual-PWM Converter in Direct-drive Wind Power Generation

MA Xian-qin，WANG Jiu-he
（SchoolofAutomation，BeijingInformationScience&TechnologyUniversity，Beijing100192，China）

Inordertoimprovetheperformanceof the converter in direct-drive wind power system，a novel hybrid control strategy based on inner loop passive and outer loop PI was presented.According to the Topology of the power circuit，both EL and PCHD model were respectively established under dq coordinate.Based on EL model，the approach called injecting damping can be adopted to obtain the control law.While，based on PWM inverter，energy forming method based on PCHD model and the IDA-PBC control algorithm were adopted to design passivity-based controller.The simulation results showed that PWM rectifier can achieve speed control.The grid-side inverter can realize voltage control at DC side andunitypowerfactoratACside.Finally，thecontrolstrategywasprovedfeasiblebyexperimentalresults.

permanent magnet synchronous machine；dual pulse width modulation（PWM）converter；passivitybased control；injecting damping；port control Hamiltonian with dissipation（PCHD）

TM315

A

1003-8930（2013）06-0035-07

马先芹（1986—），女，硕士研究生，研究方向为直驱风力发电机系统变流器控制研究。Email：wlxmaxianqin@126.com

2013-07-04；

2013-08-11

国家自然科学基金资助项目（51077005）；北京市高校创新能力提升计划项目（PXM2013_014224_000095）；北京市教委科技发展计划面上项目（SQKM-201211232009）；北京市青年拔尖人才培育计划项目（CIT&TCT201304111）

王久和（1959—），男，博士，教授，博士生导师，研究方向为电力电子技术和电力传动、非线性控制理论与应用。Email：wjhyhrwm@163.com