认知无线视觉传感网络机会传输的分布式跨层优化

由 磊，雷建军

(天津大学电子信息工程学院，天津 300072)

认知无线电能够使非授权用户(称为次用户，secondary users)通过频谱感知技术 “机会式地”(opportunistically)接入到未被授权用户(称为主用户，primary user)占用的授权频段，以提高次用户的可用带宽[1-2]．无线视觉传感网络由多个集成了微型视觉传感器的无线节点组成，可以把所获取的视觉感知信息通过多节点协同方式传输到汇聚节点(Sink 节点)，进而发送到应用服务器上进行后续处理和分析．无线视觉传感器网络既具有传统无线传感器网络自组织、自愈、灵活配置、快速覆盖和低成本部署等优点，又具有传统视觉应用系统信息量丰富的特点，能够支持更广泛的智能应用，如交通监控和流量统计、辅助生活、公共行为分析和建模以及虚拟现实等[3-4]．然而适合视觉信息无线多跳传输的非授权频段的资源有限，限制了网络的规模和性能．利用认知无线电技术接入闲置的授权频段是增强无线视觉传感网络性能和实现规模应用的可行途径之一[5]．认知无线视觉传感网络的主要挑战是可用频谱或信道的随机性．由于无线节点机会式的接入到空闲授权频谱，因而其底层的链路传输容量是动态变化的．在传统的分层网络协议设计[6]原则下，上层视觉信息的发送不会自适应地匹配底层传输能力的改变，因而不能充分利用认知无线电所带来的好处．这就需要采用跨层设计方法让上层应用实时感知下层链路上可能的传输机会，以增强视觉信息的端到端服务质量．另一方面，为了保持网络的有效性、实时性和可扩展性，所设计的算法必须是能够分布式运行的．当前关于认知无线多跳网络或无线传感网络的研究大多集中在频谱感知技术[2，7]、认知信道的分配[8]、认知MAC 协议设计[9]、认知路由[10-11]和认知无线网格网络频谱共享[12]等方面．笔者针对认知无线电的随机性，通过联合控制视觉感知信息的压缩速率、路由和链路流速率的跨层设计来提高整个无线视觉传感网络的平均性能，同时提出了跨层设计的分布式实现算法，并通过仿真验证了其收敛性和最优性．

1 网络模型和问题描述

1.1 网络模型和假设

一个无线视觉传感网络的拓扑如图 1 所示．配置摄像头的无线传感器节点按照一定的策略部署在监控区域内．节点除了监控以外，还可以协同传输视觉信息(图像序列或视频等)到汇聚节点(Sink)．虽然可以使用非授权频段(如ISM 2.4,G)作为公共传输信道，但其带宽无法完全满足视觉信息的传输要求．为了提高链路速率和网络容量，每个节点还具有认知无线电的功能，即节点可以实时感知(但无法提前预测)其链路的可用授权频段，以机会式地接入这些空白频段进行视觉感知信息的传输．

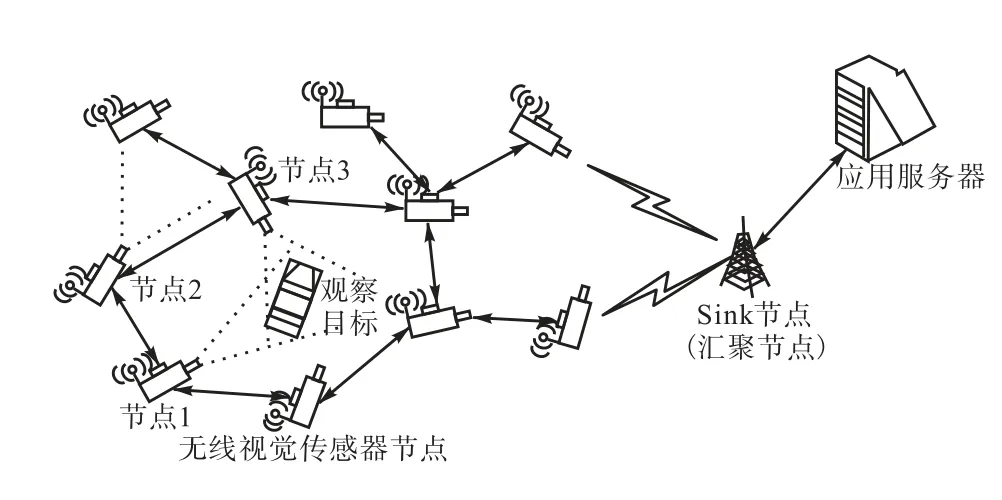
图1 无线视觉传感器网络Fig.1 Wireless visual sensor network

认知无线视觉传感网络拓扑可以用有向图G =(V,E) 来表示，其中 V 表示节点集合，而 E 表示无线链路集合．用 T 表示当前发送监控视觉信息的源节点集合(如图1 中的节点1 和节点3)．集合V、E和 T 的元素分别用 n 、l 和 m 表示，其元素数分别为N、L 和 M ．另外，节点 i 和节点 j 之间的链路也可以用(i，j)表示．假设网络部署区域内有 B 个授权频带(或信道)．由于主用户的移动性或随机接入性，这些频段的可用与否是随机变化的．在某一时刻网络中链路的可用信道状态用矢量 φ={sl,b}表示，其中sl,b= 1表示链路 l 可用信道 b(即该信道未被主用户占用)，否则 sl,b= 0．用Φ表示所有可能φ 的状态空间，即φ∈Φ．π (φ )表示信道状态φ 的静态概率分布．本文中假设网络采用 CDMA 的接入技术．采用文献[13]中码分配算法为每条链路一个低相关性的扩频码．这样，链路可以同时传输而相互干扰很少.链路 l 在状态φ 时的链路容量可以表达为Cl( φ)=Wl( φ) l b( 1 + K ξl(φ ))，其 中 Wl(φ )表 示 链 路 l在状态φ 时的可用带宽，为信道b 的带宽．ξl(φ )表示链路l 的在状态φ 时的接收信号干扰噪声比(SINR)．K 为常数．注意本文的设计方法也可以较容易地扩展到采用其他接入方式(如TDMA 或OFMDA 等)的网络．链路l 的平均容量为

源节点所产生的视觉信息是连续的图像序列(或视频)，用峰值信噪比 PSNR 来表示信息传输质量.视觉感知节点源 m 的 PSNR 可以表示为Qm=10lg DwcDm，其中Dm表示源m 的压缩MSE(均方误差)失真，而Dwc表示最坏情况的 MSE．当每个像素用 8,bit 表示时，Dwc= 2 552．根据文献[15]，D m与视频的压缩速率rm有关，可以表示为

由于网络可用信道的随机性以及所有信息都发往同一个Sink 节点，采用多径路由，即允许视觉信息在所有可能的链路上发送，而由第3 节中所提出的分布式算法决定链路上的流速率．用 fl表示链路流速率，而用 F =[ f1,…,fL]T表示所有链路流速率矢量．定义一个N × L的节点链路关联矩阵Η ，其元素hnl=1表示节点 n 是链路 l 的发射节点，而 hnl= −1 表示节点 n 是链路 l 的接收节点，否则 hnl= 0．定义R=[,…,]T为所有视觉传感节点的源速率矢量，其中=0,n ∉ T ．网络中每个节点来必须满足流均衡原则，即流出该节点的数据速率与流入速率之差必须大于该节点的信息速率，即

另外，链路分配的流速率必须小于链路的平均容量，即

1.2 视觉信息传输的跨层设计问题表达

对于实时监控来说，除了传输质量，传输时延也是一个重要的性能参数．一般来说，无线视觉传感器网络所有监控源节点的优先级是等同的，因此可以考虑优化整个网络的平均(或总)时延(而不是单个源的端到端时延)，以提高整个网络的实时性能．在M/M/1 队列模型的假设下，单位数据流在链路l 上的时延为1/(Cl(φ)−fl)[17]．可见链路时延也是依赖于φ的随机变量．链路 l 上单位数据流时延的期望定义D=[ d1,…,dL]T．对于协同多径传输的无线视觉传感器网络来说，视觉信息流可以在各个链路和端到端路径上自适应分配，以避免某些链路过分拥塞导致网络平均时延太大．

无线视觉传感器网络跨层设计的目标是在底层可用授权信道随机性和多径路由条件下，最大化网络视觉信息的传输质量和最小化传输时延．然而这两个设计目标不可能同时满足，为此可以通过引入权值β=[β1,…,βL]T来达到两个优化目标的权衡．因此，最优跨层设计问题可以表达为

式中，L=[1,…,1 ]T．权值β 衡量传输质量Θ 与时延D 的重要程度，可以根据网络的运营策略和实际部署场景等进行取值．由于Θ 和链路时延D 分别是源速率R 和F 的凸函数，因此问题(3)是一个随机凸优化问题[18]．如果可以预先获知网络的状态空间Φ 及其每个状态静态概率 π(φ)，则可以采用经典的非线性优化算法(如牛顿法、内点法等)来求解[18-19]．由于状态的静态概率很难精确获得以及需要全网传播状态和控制信息，这些集中式算法无法在网络实际运行中采用，而只能用在网络前期规划和性能估计中．为此，应用随机规划的相关理论提出了一种分布式跨层传输算法，可以作为认知无线视觉传感网络的实用传输协议，并且能够获得与(已知状态概率条件下的)集中式算法相似的优化性能．

2 随机次梯度法求解

通过对约束条件式(1)和式(2)引入拉格朗日乘子λ=[λ1,…,λN]T和μ=[μ1,…,μL]T，可以获得问题式(3)的拉格朗日函数为

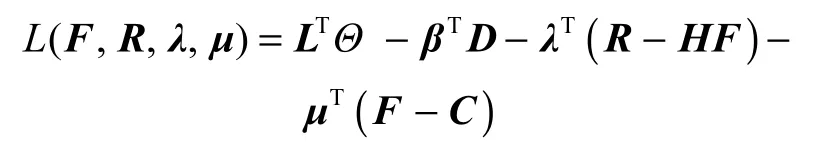
则式(3)的对偶问题的目标函数为

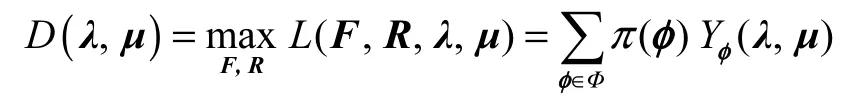
式中

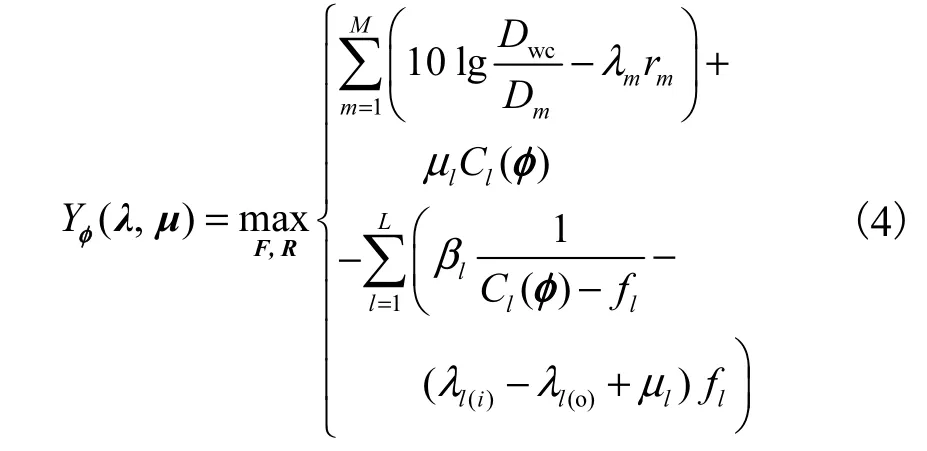
式中下标l(i) 表示链路l 的接收节点，而l(o) 表示链路l 的发射节点．因此式(3)的对偶问题[18]为

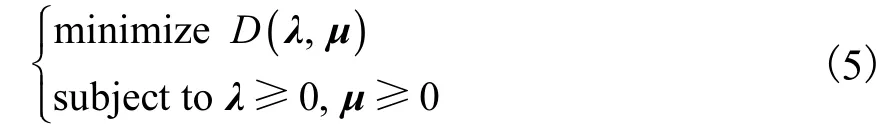
式中λ 和μ 变成了对偶问题的优化变量．由于式(3)是一个凸优化问题，因此可以通过求解其对偶式(5)来获得原问题的最优解(二者的对偶间隔为0)[18]．对偶问题式(5)也是一个随机优化问题，可以采用 “随机次梯度更新法”[19]来求解．假设在第t 步循环中对

偶变量为 λ(t)和 µ(t)，则在t+1 步进行如下方式的更新，即

式中：上标“+” 表示取值大于等于 0；θ (t) 和 ρ(t) 分别是变量 λ 和 µ 的更新步长；Χ(t) 和 Ζ(t) 分别为D (λ,μ)在 λ(t)和 µ(t)处的随机次梯度，都是随机变量．根据文献[16-17]Danskin 定理，Χ (t)和 Ζ(t)计算式为

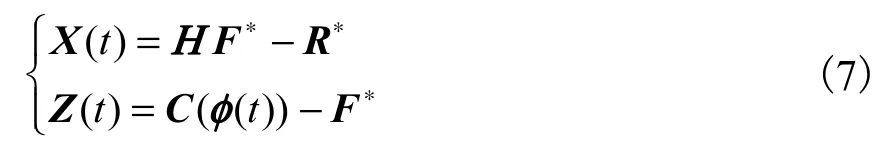
式中：φ(t)为 t 时刻网络的信道状态；C(φ(t))是 t 时刻链路瞬时容量矢量；R∗和 F∗分别是最大化问题(4)在对应状态φ(t)时源速率和链路流速率的最优解．注意到最大化问题式(4)可以进一步分解为M +L 个独立的子问题，即

(1) M 个独立的源速率控制子问题

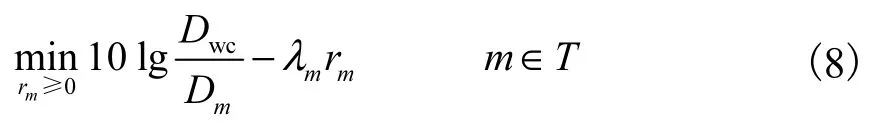
(2) L 个独立的链路数据流分配子问题

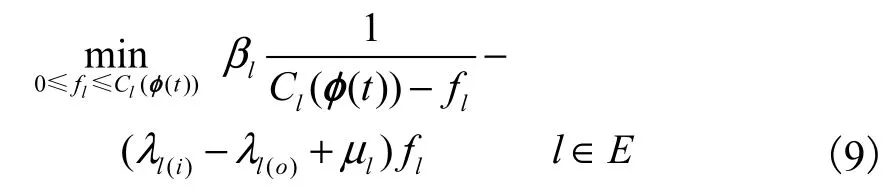
式(8)和式(9)中的各个子问题可以采用拉格朗日法[17]求解．其中，式(8)中每个子问题的解为

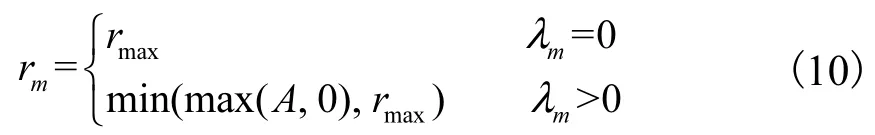
式中： rmax为视觉节点的最大可能感知速率；而 式(9) 中 每个子问题的解为

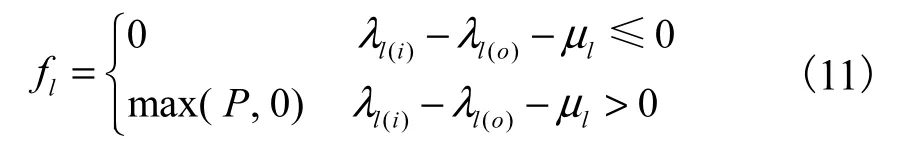
3 分布式机会传输算法

对第 2 节中随机次梯度求解过程进行仔细分析后，可以发现：①对偶变量λ 的每个分量都对应一个节点，而µ 的每个分量都与一个链路相对应；②由式(6)和式(7)可知，λ 的每个分量的更新只与其对应节点的所有链路流速率和本身产生的源速率有关，而µ的每个分量更新只与其对应链路的当前容量和承载的流速率有关；③由式(10)和式(11)可知，一个链路的最优速率和节点的最优源速率的计算只与本地对偶变量和信道状态有关．这 3 个特点都有利于算法的分布式实现．据此，提出了如下的分布式机会传输算法．该算法把随机次梯度算法的循环对应到网络传输时隙，即每个时隙更新一次对偶变量，而节点根据该时隙中所感知的信道状态自适应地进行视觉信息的网络传输．

认知无线视觉传感网络分布式机会传输算法包括初始化和算法循环．

1) 初始化

根据网络应用要求和运营策略等确定权值β；设置对偶矢量 λ(0 ) 和 µ (0)各个分量的初值，并保存在相应的节点中(μl保存在链路l 的发射节点)；设置固定步长θ和δ；确定网络中链路可用的B 个授权频段；链路的发射节点测量并保存该链路上信道的SINR；离线或在线估计每个源视觉节点参数、θm和．

2) 算法循环

在第t 个时隙有

(1) 每个节点n 向邻居节点广播对偶变量λn(i).

(2) 发送视觉信息的源节点m ∈ T，根据式(10)计算当前视频发送速率 rm．

(3) 每条链路 l 的发射节点测量该链路的可用授权信道，计算链路瞬时速率并根据式(11)计算本时隙内可发送的流速率 fl．

(4) 根据步骤(2)和(3)的计算结果进行信息传输．

(5) 每个节点根据本地链路容量、流速率和视频源速率，按照式(7)计算相应的随机次梯度，并按照式(6)更新其对应的对偶变量．

上述过程循环执行，直到收敛．

上述算法中每个时隙内节点向邻居节点广播自己的对偶变量，并根据收到的对偶变量独立地计算与本节点相关的源速率、链路速率、随机次梯度和对偶变量．这种分布式算法避免了集中式算法在全网传播控制信息和状态信息的问题．另外，算法不需要预先估计可用授权信道状态的静态概率分布，只需要节点(如算法的步骤(3)所述）感知当前时隙中授权信道的可用性，使链路能够进行机会传输．视觉源节点通过对偶变量实现对底层认知信道的自适应匹配，因而能够充分利用认知无线电增强网络性能．分布式算法的收敛性和最优性将通过第4 节的仿真给出．

4 仿真结果与分析

4.1 仿真场景与参数

采用如图 2 所示的无线视觉传感网络拓扑来验证所提出的分布式机会传输算法的收敛性和最优性．该拓扑中包含 16 个无线视觉传感节点，均匀分布在一个300 m ×300 m的区域内．假设该区域有4 个可用的授权频段，同时为了保持网络的连接性还使用一个固定的 ISM 非授权频段．每个频段的信道带宽设为 1,MHz．对于网络每个链路来说，授权频段的可用概率是独立同分布的．设4 个授权频段被主用户占用的静态概率分别为 0.5、0.2、0.3 和 0.4．所有链路在每个可用信道上的发射功率固定为 Pt= 5 00 mW ，接收噪声为3 mW ，接收功率只考虑自由空间路径损耗，假设为Pr=ξd−3Pt，其中ξ为常数，设为105，d 为链路传输距离，m．设置节点 1 、4 和 9 为当前需要发送视觉信息的源节点，节点 16 为汇聚节点，其余节点作为中继节点．设 rmax=10．假设3 个源节点视觉信息的 PSNR 特征参数分别为= 1 .380，θ1= 1 .830，

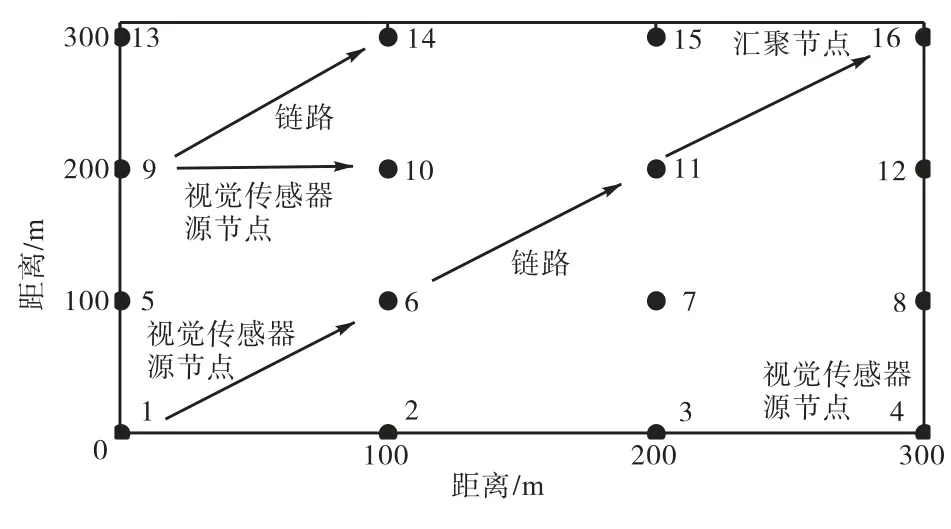
图2 仿真拓扑示意Fig.2 Topology for simulations

4.2 算法的收敛性

验证在整个网络运行的分布式算法能够通过节点的本地信息交换使得优化变量协同收敛到稳定(平均)值．为了便于仿真结果显示，在不失一般性的情况下，权值β各个分量设为βl=2 0,l ∈ E ．图3显示了3个视觉传感器节点 1 、4 和 9 的源速率随着算法循环的变化情况．可见，源速率在 4 00 次循环后基本能够收敛到一个稳定值，3 个源速率最终收敛的稳定平均值分别为3.053,3,Mb/s 、2.497,4,Mb/s 和3.481,0,Mb/s．图4显示了链路(1，2)和(4，8)上瞬时流速率和平均流速率随着算法循环的变化．由于认知无线电的随机性，每个循环(相当于每个传输时隙)中链路可用信道和链路容量是随机变化的，链路的瞬时传输速率也随着链路容量的变化而变化．然而链路的平均流速率可以收敛到一个稳定值．如图4所示，链路(1，2)和(4，8)的平均流速率在大约 200 次循环后收敛到 1.556,1,Mb/s 和 2.428,9,Mb/s．这表明：所提出的跨层优化算法能够通过节点的局部信息交换和分布式计算使源速率和链路流速率收敛．

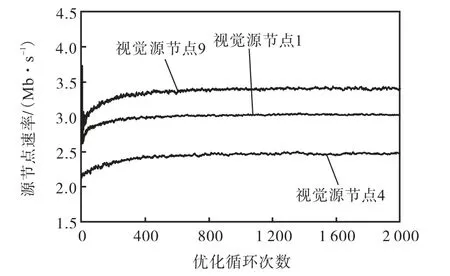
图3 3个视觉传感节点源速率的收敛性Fig.3 Convergence of source rate of three visual sensor nodes

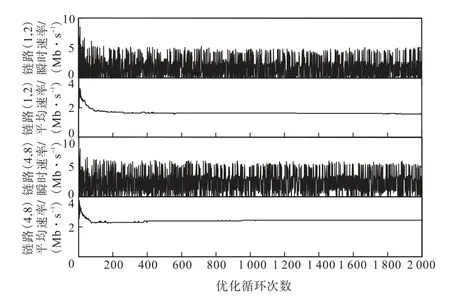
图4 链路(1，2)和(4，8)流速率的收敛性Fig.4 Convergence of flow rate of links(1,2)and(4,8)

4.3 算法的最优性

如果已知网络的信道状态及其概率分布，可以采用集中式的非线性优化算法求得式(3)的最优解.通过与集中式算法比较来说明所提出的分布式算法的最优性．集中式算法采用 “序列二次规划算法”，并在 M atlab 中用 F mincon 函数得到优化结果．表 1 为设置权值βl= 20、l ∈ E时，采用分布式算法和集中式算法所得到节点的平均流入和流出速率的比较．节点1、4 和9 是源节点，因而没有流入速率，只有流出速率，且平均流出速率与平均源速率相等(见图3)．节点16 是汇聚节点，没有流出速率，只有流入速率，且流入平均速率与 3 个源速率之和相等．其余节点数据中继节点既有流入速率，又有流出速率．从表1 中可以看出，分布式算法与集中式算法所获得优化结果非常接近，特别是视觉源节点的发送速率．

表 2 为设置不同的权值β时，集中式算法与分布式算法所获得的平均 PSNR、平均网络时延和式

(3)的优化目标值的比较．减少β值相当于降低了网络时延的权重．由表 2 可以看出，随着β值的降低，网络可以通过容忍更大的时延来换取视觉信息平均PSNR 的提高．同时，β= [ 200100 20 51]时，分布式算法可以获得与集中式算法相近的平均 PSNR、平均时延和优化目标值．值得注意的是当β=0 (即不考虑网络时延)时虽然分布式算法所获得的平均PSNR 和优化目标值略低于集中式算法，但其平均时延却比集中式算法小得多．集中式算法平均时延为 4.048,6×1016,ms/(Mb/s)，这实际上相当于无穷大，无法实现实时监控的目的．

表 1 和表 2 的优化数据表明：分布式算法能够获得与集中式算法相似的优化性能，而分布式算法不需要预先知道或估计认知网络的信道状态的概率分布，只需实时感知网络的瞬时信道状况即可动态适应和充分利用网络的传输机会，并且具有可扩展性和实时性保证，因此该算法对于认知无线视觉传感器网络的规模应用具有一定的实用价值．

表1 分布式算法与集中式算法节点平均流入和流出速率优化结果比较( βl=2 0,l ∈ E)Tab.1 Comparison of average input and output flow rate of nodes of distributed and centralized algorithms( βl=2 0,l ∈ E)(Mb·s-1)

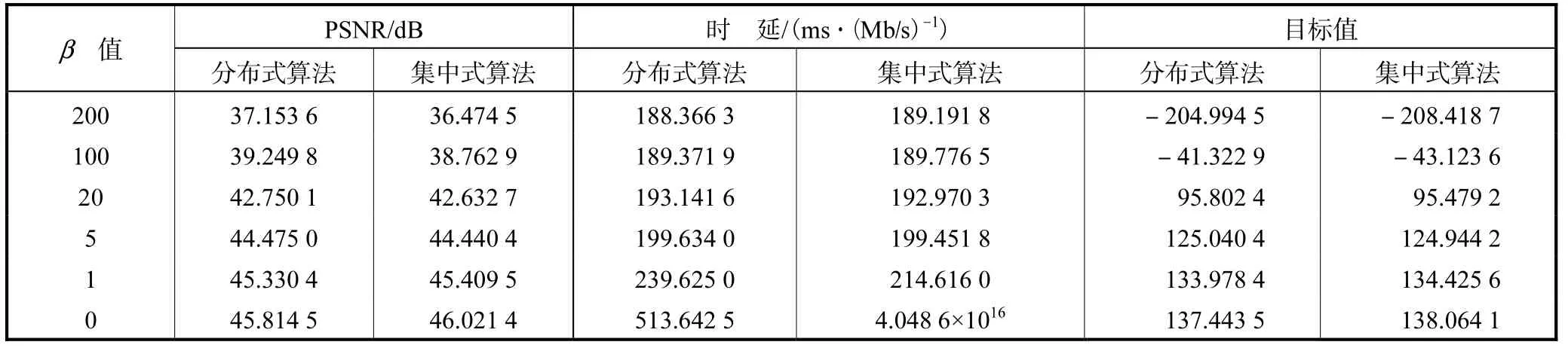
表2 分布式算法与集中式算法平均PSNR、平均传输时延和优化目标值优化结果比较Tab.2 Comparison of average PRNR，delay and optimal objective value of distributed and centralized algorithms

5 结 语

研究了认知无线视觉传感网络的跨层设计方法，并提出了一个分布式优化算法．通过联合控制上层视觉信息的压缩速率和底层认知链路的机会传输达到端到端服务质量和网络平均时延的权衡最优化．通过对偶分解和随机次梯度法求解该优化问题，推导出一个可以分布式实现的跨层优化算法．该算法不需要预知可用频段的静态概率分布，能通过本地计算和信息交换达到全网控制参数和端到端视觉信息传输的最优化．本文中所提出的算法能够为认知无线视觉传感网络的大规模部署和传输协议设计提供实用参考．

在网络模型和仿真中假设节点在每个信道上的发射功率是固定的，而对于电池或太阳能供电的无线视觉传感网络设计能量有效的传输协议是非常必要的．今后将进一步研究怎样将功率分配和能量控制集成到所提出的跨层设计方法和分布式算中．

［1］Akyildiz I F，Lee W-Y，Vuran M C，et al. Next generation/dynamic spectrum access/cognitive radio wireless networks：A survey[J].Computer Networks(Elsevier)，2006，50(13)：2127-2159.

［2］Haykin S. Cognitive radio：Brain-empowered wireless communications[J].IEEE Journal on Selected Areas in Communications，2005，23(2)：201-220.

［3］Soro Stanislava，Heinzelman Wendi. A Survey of visual sensor networks[J].Advances in Multimedia，2009：Article ID 640386.

［4］Charfi Y，Wakamiya N，Murata M. Challenging issues in visual sensor networks[J].IEEE Wireless Communications Magazine，2009，16(2)：44-49.

［5］Akyildiz I F，Melodia T，Chowdhury K R. A survey on wireless multimedia sensor networks[J].Computer Networks(Elsevier)，2007，51(4)：921-960.

［6］由 磊. 无线多跳网络跨层设计与优化的相关理论和算法研究[D]. 北京：北京邮电大学电子工程学院，2009.You Lei. Research on the Theory and Algorithms of Cross-Layer Design and Optimization for Wireless Multihop Network[D]. Beijing：School of Electronic Engineering，Beijing University of Posts and Telecommunications，2009(in Chinese).

［7］Zhao Q，Sadler B. A survey of dynamic spectrum access[J].IEEE Signal Process Mag，2007，24(3)：79-89.

［8］AL-Fuquha A，Khan B，Rayes A，et al. Opportunistic channel selection strategy for better QoS in cooperative networks with cognitive radio capabilities[J].IEEE Journal on Selected Areas in Communications，2008，26(1)：156-167.

［9］Cordeiro C，Challapali K. C-MAC：A cognitive MAC protocol for multi-channel wireless networks[C]//IEEE DySPAN. Dublin，Ireland，2007：147-157.

［10］Cheng G，Liu W，Li Y，et al. Joint on-demand routing and spectrum assignment in cognitive radio networks[C]//IEEE ICC. Glasgow，Scotland，2007：6499-6503.

［11］郑腾飞，朱 琦. 认知 Ad Hoc 网络中的跨层路由协议[J]. 计算机应用，2011，31(增2)：9-13.

［12］Zheng Tengfei，Zhu Qi. Cross-layer routing protocol for cognitive Ad Hoc networks[J].Journal of Computer Applications，2011，31(Supl2)：9-13(in Chinese).

［13］Chowdhury K R，Akyildiz I F. Cognitive wireless mesh networks with dynamic spectrum access[J].IEEE Journal of Selected Areas in Communications， 2008 ，26(1)：168-181.

［14］Hu L. Distributed code assignments for CDMA packet radio networks[J].IEEE/ACM Trans Networking，1993，1(1)：668-677.

［15］由 磊，雷建军，王丕超. 无线多跳网络中SVC 视频流传输的分布式优化方法[J]. 天津大学学报，2013，46(1)：73-78.You Lei，Lei Jianjun，Wang Pichao. Distributed optimization method for SVC streaming in wireless multihop networks[J].Journal of Tianjin University，2013，46(1)：73-78(in Chinese).

［16］Stuhlmuller K，Farber N，Link M，et al. Analysis of video transmission over lossy channels[J].IEEE Journal on Selected Areas in Communication，2000，18(6)：1012-1032.

［17］Pudlewski S，Prasanna A，Melodia T. Compressedsensing-enabled video streaming for wireless multimedia sensor networks[J].IEEE Transactions on Mobile Computing，2012，11(6)：1060-1072.

［18］Bertsekas D，Gallager R.Data Networks[M]. New York，USA：Prentice Hall，2000.

［19］Bertsekas D P.Nonlinear Programming[M]. Belmont，USA：Athena Scientific，1999.

［20］Kall Peter ， Wallace Stein W.Stochastic Programming[M]. 2nd,ed. Chichester，UK：John Wiley and Sons，1994.