随机分布贯穿裂隙岩体峰后应力-应变关系模型
2013-06-04仝兴华韩建新李术才李树忱汪雷
仝兴华,韩建新, ,李术才,李树忱 ,汪雷,
(1. 山东大学 岩土与结构工程研究中心,山东 济南,250061;2. 山东财经大学 数学与数量经济学院,山东 济南,250014;3. 工程兵学院,江苏 徐州,221004)
由于地质构造运动等原因,工程岩体通常含有随机分布的贯穿裂隙,在开挖等人工干扰作用下,这些裂隙岩体经常处于峰后状态,具有一定的承载能力,但由于应变软化的影响,当岩体变形发展到一定的程度之后,结构会突然失稳,导致结构的动态破坏失效,造成人力、物力上的损失,因此研究随机分布的贯穿裂隙岩体峰后变形具有重要的理论和工程意义。在研究岩石材料的峰后变形方面,国内外学者从不同角度已做了很多工作。比较典型的有Fang等[1-2]利用峰后强度下降指数描述围压对岩石峰后残余强度和割线模量的影响,建立了考虑围压影响的岩石峰后应变软化力学模型。Armaldi等[3-4]利用统计损伤模型对峰后变形进行了研究。王学滨等[5]基于梯度塑性理论对岩石进行了峰后变形特征研究。王水林等[6]基于Mohr-Coulomb准则,采用数值试验对岩土介质的峰后应力-应变曲线进行了研究。陆银龙等[7]通过建立以广义黏聚力c和广义内摩擦角φ这2个状态参数来表征的软弱岩石后继屈服面模型,对软弱岩石的峰后力学特性进行了研究。李文婷等[8]基于Mohr-Coulomb强度准则,以内摩擦角作为中间变量,通过理论推导,将峰后弹性模量表征为应变的函数,建立了峰后岩体力学非线性应力–应变关系。Saeb等[9-12]则对节理的峰后应力-位移关系进行了研究。以上成果对于开展裂隙岩体的峰后应力-应变关系研究有着非常重要的借鉴作用。但这些成果要么是对岩石进行峰后变形研究,要么是对节理进行峰后变形研究,而对随机分布的裂隙岩体进行峰后变形研究还很少见到,本文作者将基于强度参数的演化行为,采用Mohr-Coulomb强度准则,对随机分布的贯穿裂隙岩体峰后应力-应变关系开展 研究。
1 岩石峰后应力-应变关系和裂隙的峰后应力-位移关系的求法
在岩石峰后变形阶段,岩石的黏聚力和摩擦角一般随着最大主应变的增加而发生变化,或者说由于黏聚力和摩擦角这2个强度参数的变化,才导致了峰后应变软化,而在裂隙的峰后变形阶段,裂隙的黏聚力和摩擦角则随着裂隙剪切变形而发生变化,根据在岩石或裂隙的峰后变形阶段强度参数逐渐演化这一事实,下面基于Mohr-Coulomb强度准则,分别以岩石的最大主应变ε1和裂隙的切向位移us作为软化参数,求岩石峰后应力-应变关系和裂隙的峰后应力-位移关系。
1.1 岩石峰后应力-应变关系的求法
在岩石的峰后应变软化阶段,黏聚力c和摩擦角φ随着最大主应变 ε1的增加而变化,所以Mohr-Coulomb强度准则可表示为:
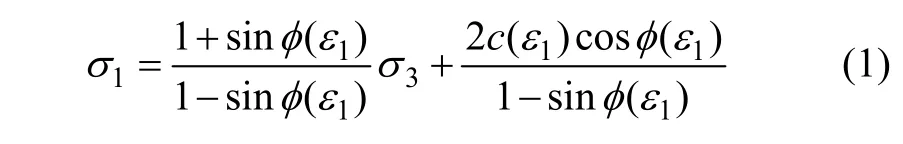
其中:σ1为最大主应力;σ3为最小主应力。
在确定强度参数的演化规律方面,一般可通过实验、数值模拟等方法来获取强度参数与应变软化参数之间的关系,即强度参数的演化规律。但为了使问题简化,通常假设强度参数与应变软化参数之间为分段线性函数的形式[13-14],其表达式为
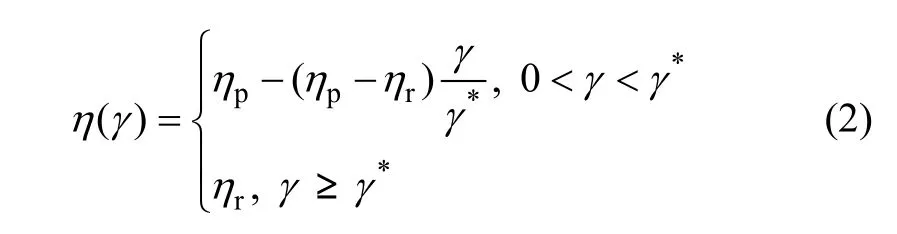
其中:η,ηp和 ηr分别为强度参数,峰值处的强度参数值和残余阶段的强度参数;γ*为应变软化参数 γ在残余阶段开始处的值。对应的演化曲线如图1所示。
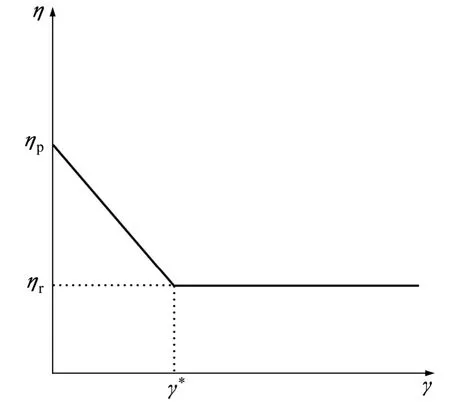
图1 强度参数的演化曲线Fig. 1 Evolutional curve of strength parameter
本文选择Mohr-Coulomb准则作为强度准则,主应变ε1作为应变软化参数,因此需要确定黏聚力c,摩擦角φ和 ε1之间的关系。由式(2)可得岩石材料强度参数c和φ的演化规律如下:
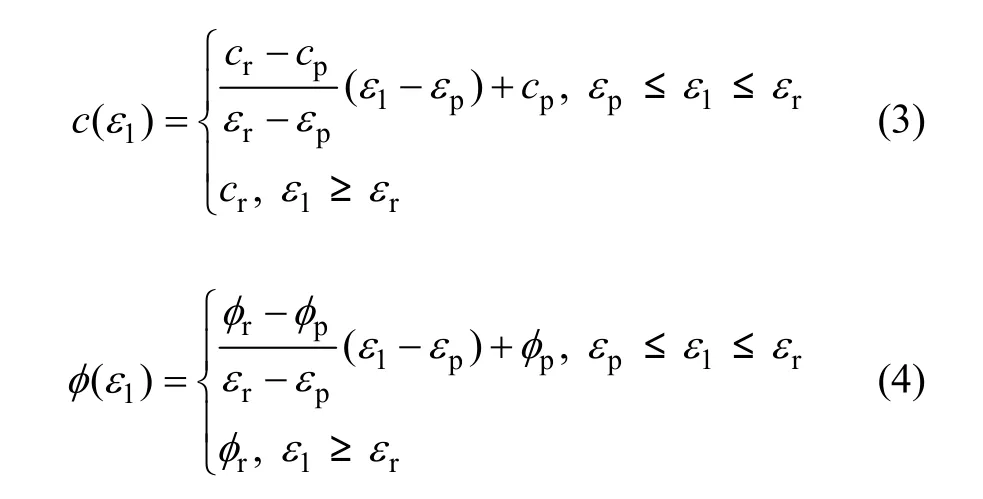
其中:εp,cp和φp分别为峰值处的主应变,黏聚力和摩擦角;εr,cr和φr分别为残余强度开始处的主应变、黏聚力和摩擦角,可通过岩石实验测得。将式(3)和(4)代入式(1),即可求出岩石峰后应力-应变关系表达式。
1.2 裂隙峰后应力-切向位移关系的求法
图2所示为1条贯穿裂隙岩体模型。如图2所示,设试块内含有一条倾角为β的裂隙。对于裂隙来说,在峰后软化阶段,其黏聚力cw,摩擦角φw随着切向位移us的增加而变化,所以裂隙的 Mohr-Coulomb强度准则可表示为:
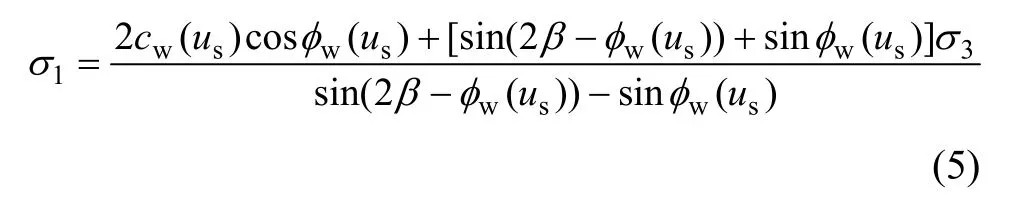
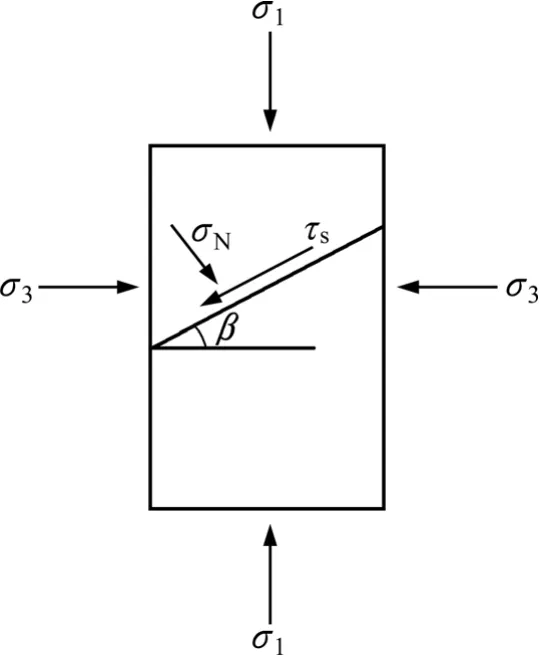
图2 1条贯穿裂隙岩体模型Fig. 2 Model of rock mass with one penetrative crack
为了使问题简化,假设裂隙黏聚力cw,摩擦角φw的演化规律为:
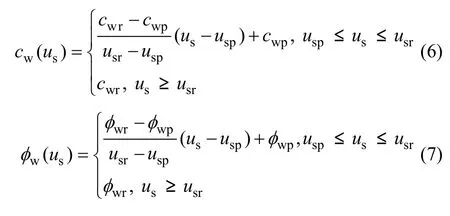
其中:εwp,cwp和φwp分别为峰值处的最大主应变、黏聚力和摩擦角;εwr,cwr和φwr分别为残余阶段开始处的最大主应变、黏聚力和摩擦角;usp和 usr分别为峰值处的切向位移和残余阶段开始处的切向位移,其值均可由实验得到。将式(6)和(7)代入式(5),即可求出裂隙峰后应力-切向位移表达式。
2 随机分布贯穿裂隙岩体峰后应力-应变关系模型
图3所示为随机分布贯穿裂隙岩体模型。如图3所示,设岩体的高为h,岩体中含有n条随机分布的贯穿裂隙,裂隙的倾斜角为β,裂隙的摩擦角均为φw,黏聚力均为cw,岩石的黏聚力和摩擦角分别为c和φ,裂隙沿竖直方向的平均间距为,岩体所受轴压为σ1,所受围压为σ3。为建立模型,提出如下3个假设:
(1) 在岩石的峰前变形阶段,岩石为各向同性的线弹性体:设岩石的弹性模量为 E,泊松比为 ν,轴向应变为εi,则有
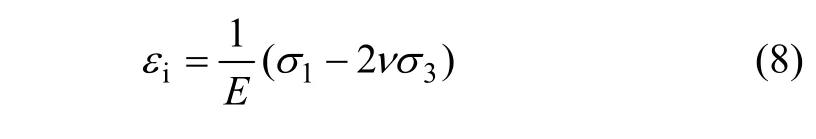
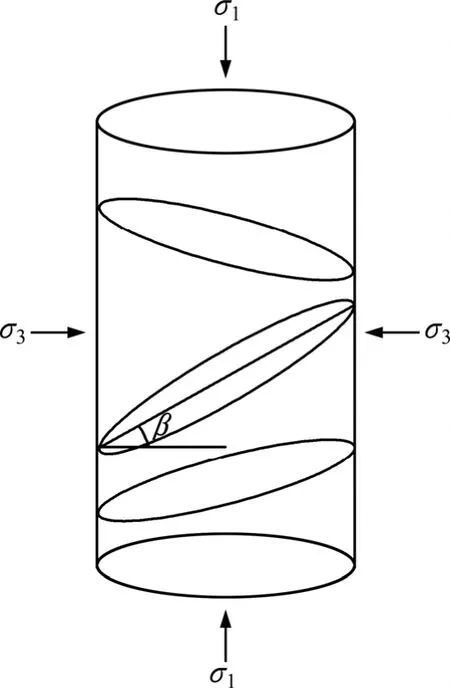
图3 随机分布贯穿裂隙岩体模型Fig. 3 Model of rock mass with random distribution of penetrative crack
(2) 在裂隙的峰前变形阶段,裂隙的切向应力和切向位移满足线性刚度关系,而法向应力和法向位移在峰前、峰后始终满足线性刚度关系。设裂隙法向刚度为 kN,法向应力为 σN,法向位移为 uN,剪切刚度为ks,剪切应力为τs,剪切位移为us,则在裂隙的峰前变形阶段有

在整个变形过程中有

(3) 各裂隙间的变形相互独立。
2.1 裂隙峰前变形阶段裂隙轴向总位移的求法
根据莫尔应力圆方法,可求得倾斜角为β的裂隙面上的法向应力和剪切应力分别为:
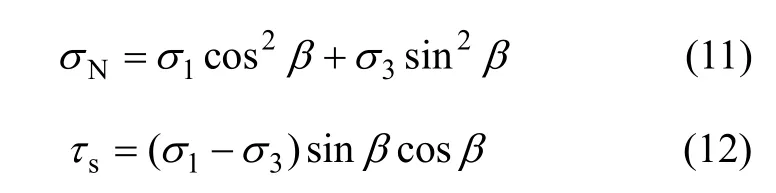
由模型假设可得法向位移和切向位移分别为:
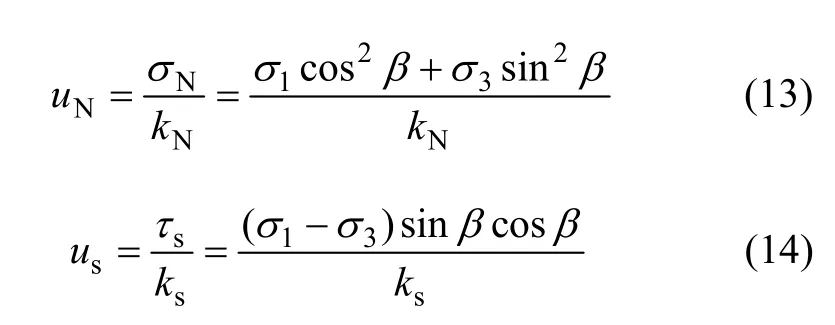
所以该裂隙的轴向位移为:
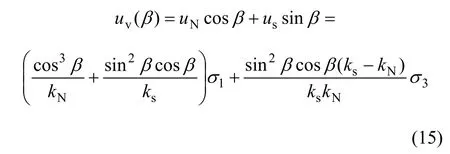
由式(10)可得各裂隙的平均位移为:
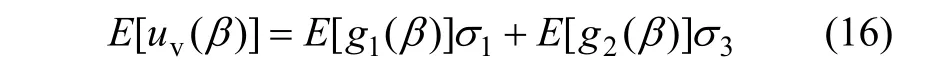
其中:
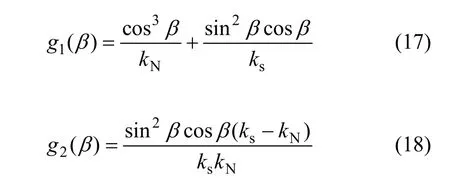
假设裂隙倾角的密度函数为 f(β),沿竖直方向的裂隙间距的密度函数为f(S),其中S表示竖直方向的裂隙间距,则所有裂隙的总位移为:
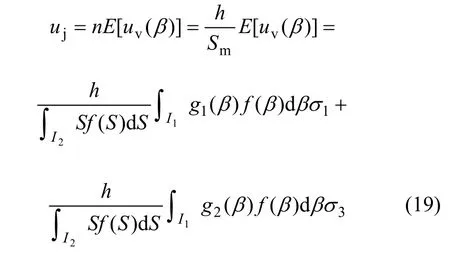
其中:I1和I2分别为裂隙倾角β、裂隙间距S可能取值的集合;Sm为裂隙平均间距。式(19)即为所有裂隙轴向位移的计算公式,在裂隙材料参数和几何参数已知的情况下,可由式(19)计算裂隙的位移。
2.2 随机分布贯穿裂隙岩体峰后应力-应变关系的求法
在岩体峰后软化阶段,岩体处于卸荷破坏状态,岩石要么沿着裂隙面滑移破坏,要么沿着岩石剪切破坏,下面分 2种情况研究裂隙岩体的峰后应力-应变关系的求法。
(1) 当岩体沿着裂隙滑移破坏时,岩体的轴向位移由滑动裂隙的轴向位移、未滑动裂隙的轴向位移和岩石的轴向位移组成。根据模型假设可得岩石的轴向位移
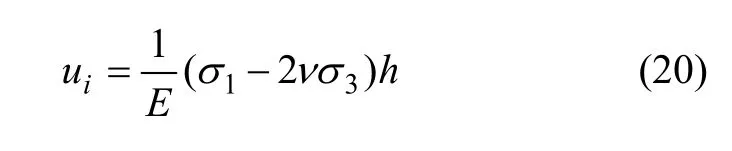
假设岩体沿着第k条裂隙破坏,设该裂隙切向位移为us,倾角为βk,则由该滑动面切向位移引起的轴向位移为
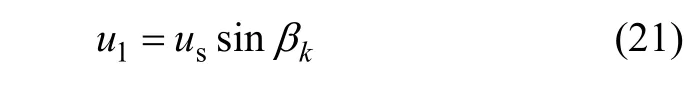
考虑滑移裂隙破坏前的切向位移远远小于破坏后的切向滑移位移,由式(19)可得由滑移裂隙的法向位移引起的轴向位移和其余裂隙的轴向位移之和u0为:
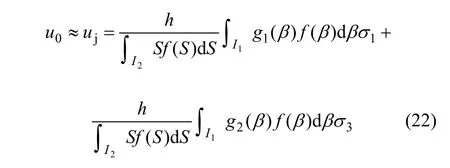
将式(20),(21)和(22)相加,最后除以岩体的高度h即可求得岩体的峰后应力-应变关系式为:
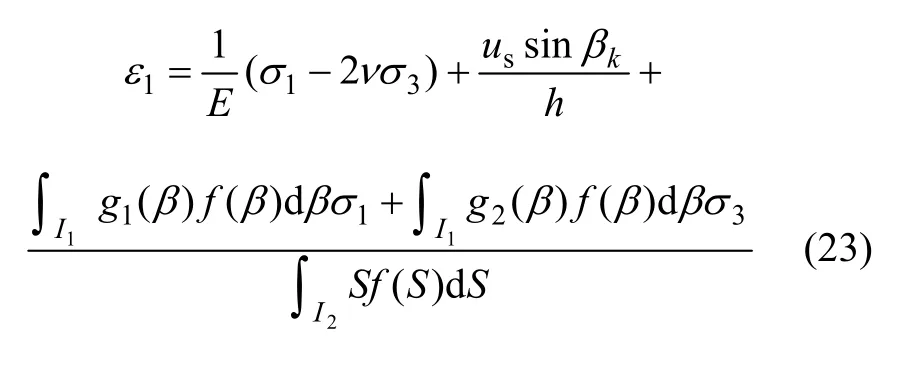
由于岩体沿着第k组的某条裂隙破坏,所以由裂隙的 Mohr-Coulomb强度准则可得(23)式中 σ1应满足式(5)。将式(5),(6)和(7)代入式(23),即可求得岩体的峰后应力-应变关系式。因表达式过于冗长,这里不再给出。特别的,当倾角β服从区间[a,b]均匀分布,s′服从参数为λ的指数分布时,式(23)可化为:
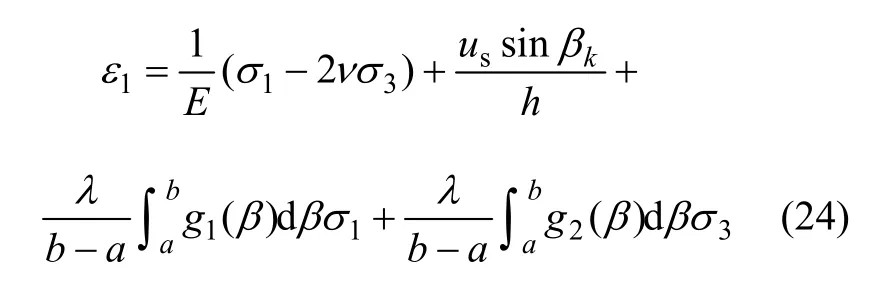
(2) 当岩体沿着岩石剪切破坏时,岩体的轴向位移由岩石的轴向位移和裂隙面的轴向位移组成,其中裂隙的轴向位移可由式(19)求得。设岩石的轴向应变为εi,则岩石的轴向位移为

将式(19)和(25)相加后除以试块的高度 h可得试块的应变为
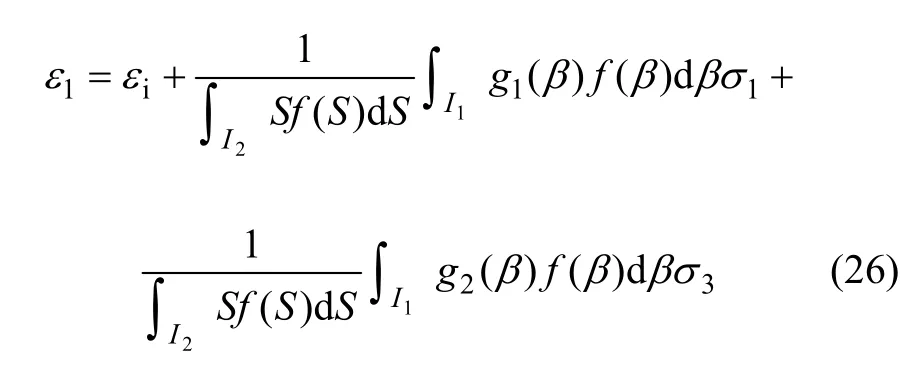
因为岩体沿着岩石剪切破坏,所以由岩石的Mohr-Coulomb强度准则可得式(26)中的 σ1应满足式(1)。将式(1)、(3)和(4)代入式(26),即可求得在给定围压下岩体的峰后应力-应变关系式,因表达式过于冗长,这里也不再列出。特别的,当倾角 β服从区间[a,b]均匀分布,S服从参数为λ的指数分布时,式(26)可化为
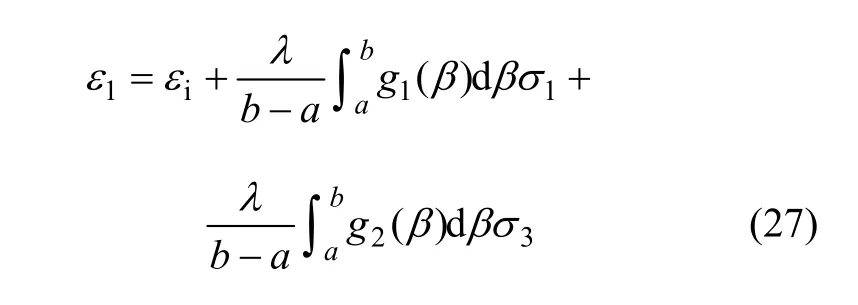
总结以上过程可以得出求贯穿裂隙岩体的峰后应力-应变关系的基本方法:首先判断岩体的破坏方式,可参照文献[16]来判断,若沿着裂隙滑移破坏,应根据式(23)来求裂隙岩体的峰后应力-应变关系,若沿着岩石剪切破坏,应根据式(26)来求裂隙岩体的峰后应力-应变关系。
3 算例
设试块是内部包含贯穿裂隙的圆柱体(高为1 m),假设贯穿裂隙倾角 β服从区间上的均匀分布,间距s服从参数为10的指数分布,即s~e(10),所有裂隙的法向刚度均为 100 GN/m3,剪切刚度均为 20 GN/m3,裂隙峰值处黏聚力为2 MPa,摩擦角为38.0°,残余阶段的黏聚力为0.2 MPa,摩擦角为30.0°,岩石峰值处的摩擦角为40.0°,黏聚力为30 MPa弹性模量为30 GPa,泊松比为0.25,试块所受围压为14 MPa,设裂隙峰值处的切向位移为0.001,残余阶段开始处的切向位移为0.02,下面求岩体的峰后应力-应变曲线。由文献[16]可知:当裂隙的倾角越接近=64°时,裂隙的强度越低,因为裂隙倾角 β服从区间上的均匀分布,可近似认为该试块中,强度最弱的结构面的倾斜角为 64°,根据所给的强度参数,由文献[16]可知:试块将沿着该裂隙面滑移破坏。将所给的参数代入式(5),(6),(7)和(24)可求得试块的峰后应力-应变关系式,其全应力-应变曲线如图(4)所示。为了研究裂隙的几何参数和物理参数对岩体峰后应力-应变曲线的影响,不同参数下的岩体的峰后应力-应变曲线如图5所示。从图5可以看出:裂隙的平均间距、法向刚度越大,裂隙岩体峰后应变越小。这是由于裂隙间距越大,同样高度内的裂隙数量越少;法向刚度和切向刚度越大,相同应力下引起的裂隙位移越小,从而使得岩体的总位移减小的结果。
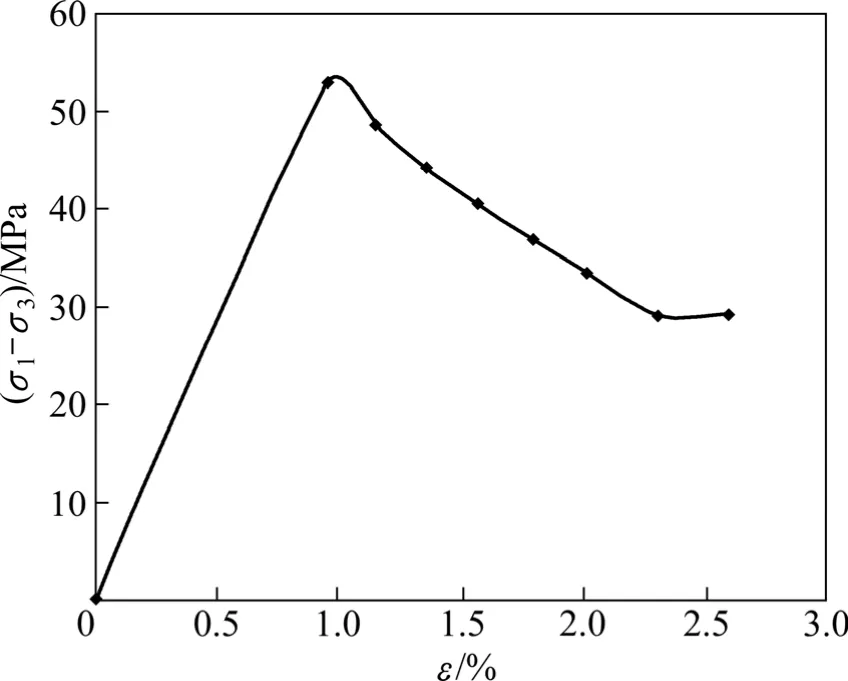
图4 裂隙岩体和岩石的全应力-应变曲线Fig. 4 Complete stress-strain curve of fractured rock mass and rock
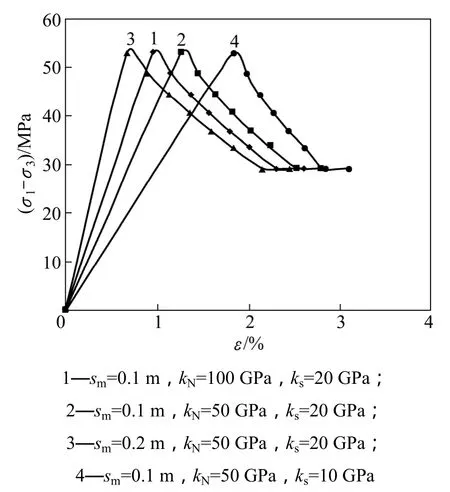
图5 裂隙参数对峰后应力-应变曲线的影响Fig. 5 Effects of crack’s parameters to post-peak stress-strain curve
4 结论
(1) 基于强度参数的演化行为,针对Mohr-Coulomb强度准则,分别以岩石的最大主应变ε1和裂隙的剪切位移us作为应变软化参数,给出了岩石峰后应力-应变关系和裂隙的峰后应力-切向位移关系的具体求法。
(2) 在岩石峰后应力-应变关系和裂隙的峰后应力-位移关系求法的基础上,通过建模,利用概率的方法给出了随机分布贯穿裂隙岩体的峰后应力-应变关系式。
(3) 结合算例,讨论了裂隙的平均间距、法向刚度和切向刚度对随机分布贯穿裂隙岩体的峰后应力-应变曲线的影响。结果表明裂隙的平均间距、法向刚度和切向刚度越大,裂隙岩体峰后应变越小。
[1] Fang Z, Harrison J P. A mechanical degradation index for rock[J].International Journal of Rock Mechanics and Mining Sciences,2001, 38(8): 1193-1199.
[2] 张春会, 赵全胜, 黄鹂, 等. 考虑围压影响的岩石峰后应变软化力学模型[J]. 岩土力学, 2010, 31(增2): 193-197.ZHANG Chunhui, ZHAO Quansheng, HUANG Li, et al.Post-peak strain softening mechanical of rock considering confining pressure effect[J]. Rock and Soil Mechanics, 2010,31(Supp.2): 193-197.
[3] Arinaldi A, Peralta P, Krajcinovic D. Prediction of scatter in fatigue properties using discrete damage mechanics[J].International Journal of Fatigue, 2006, 28(9): 1069-1080.
[4] 唐春安. 岩石破裂过程中的灾变[M]. 北京: 煤炭工业出版社,1993: 40-48.TANG Chunan. Catastrophe in rock unstable failure[M]. Beijing:China Coal Industry Publishing House, 1993: 40-48.
[5] 王学滨. 基于梯度塑性理论的岩样峰后变形特征研究[J]. 岩石力学与工程学报, 2004, 23(增1): 4292-4295.WANG Xuebin. Characteristics of post-peak deformations of rock in uniaxial compression based on gradient-dependent plasticity[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(Supp.1): 4292-4295.
[6] 王水林, 王威, 吴振君. 岩土材料峰值后区强度参数演化与应力–应变曲线关系研究[J]. 岩石力学与工程学报, 2010,29(8): 1524-1529.WANG Shuilin, WANG Wei, WU Zhenjun. Study of relationship between evolution of post-peak strength parameters and stress-strain curves of geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1524-1529.
[7] 陆银龙, 王连国, 杨峰. 软弱岩石峰后应变软化力学特性研究[J]. 岩石力学与工程学报, 2010, 29(3): 640-648.LU Yinlong, WANG Lianguo, YANG Feng. Post-peak strain softening mechanical properties of weak rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3):640-648.
[8] 李文婷, 李树忱, 冯现大, 等. 基于 Mohr-Coulomb准则的岩石峰后应变软化力学行为研究[J]. 岩石力学与工程学报,2011, 30(7): 1461-1466.LI Wenting, LI Shuchen, FENG Xianda, et al. Study of post-peak strain softening mechanical properties of rock based on Mohr-Coulomb strength criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7): 1461-1466.
[9] Saeb S, Amadei B. Modeling rock joints under shear and normal loading[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1992, 29(3): 267-278.
[10] Grasselli G. Shear strength of rock joints based on quantified surface description[D]. Lausanne: Swiss Federal Institute of Technology. Laboratory of Mechanics, 2001: 89-92.
[11] Grasselli G, Egger B. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J].International Journal of Rock Mechanics and Mining Sciences,2003, 40(1): 25-40.
[12] 唐志成, 夏才初, 黄继辉, 等. 节理峰值后归一化位移软化模型[J]. 岩土力学, 2011, 32(7): 2013-2016.TANG Zhicheng, XIA Caichu, HUANG Jihui, et al. Post-peak normalized displacement softening model for discontinuous rock joint[J]. Rock and Soil Mechanics, 2011, 32(7): 2013-2016
[13] Lee Y K, Pietruszczak S. A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rock mass[J]. Tunnelling and Underground Space Technology, 2008, 23: 588-599.
[14] Alonso E, Alejano L R, Varas F, et al. Ground response curves for rock masses exhibiting strain-softening behaviour[J]. Int J Numer Anal Meth Geomech, 2003, 27(13): 1153-1185.
[15] 韩建新, 李术才, 李树忱, 等. 贯穿裂隙岩体强度和破坏方式的模型研[J]. 岩土力学, 2011, 32(增刊2): 178-184.HAN Jianxin, LI Shucai, LI Shuchen, et al. study of the strength and failure mode of the rock mass with persistent cracks[J].Rock and Soil Mechanics, 2011, 32(Supp.2): 178-184.
