RV传动机构精度分析

杨玉虎，张 洁，许立新

(1. 天津大学机构理论与装备设计教育部重点实验室，天津 300072；2. 天津职业技术师范大学机械工程学院，天津 300222)

RV传动机构精度分析

杨玉虎1，张 洁1，许立新2

(1. 天津大学机构理论与装备设计教育部重点实验室，天津 300072；2. 天津职业技术师范大学机械工程学院，天津 300222)

以一类含渐开线和摆线的二级封闭式行星传动机构即RV(rotate vector)机构为对象，基于作用线增量原理，应用误差分析的传递矩阵法，研究了机构中各构件的原始误差在整个传动过程中对机构输出转角误差的影响规律，建立了适用于该机构精度分析的误差模型．该模型建立了各构件原始误差与机构输出误差的解析对应关系，揭示了机构中共用构件(曲柄轴等)的误差传递过程，以及由于固连输出盘与系杆导致的机构反馈误差与各构件原始误差的耦合关系，为该类机构的精度分析与设计提供了可靠的理论依据．最后,以RV320S型减速器为例，进行实例验算．结果表明，对机构输出转角误差影响最大的是输出盘上曲柄轴孔偏心误差，其次是摆线轮齿廓误差；机构的反馈误差对于高精密RV传动系统也不应忽视．

RV传动机构；误差分析模型；反馈误差；误差传递矩阵

近年来，虽然RV传动机构的研究已经取得诸多进展，但传动精度仍是制约这类机构应用于高精密工业机器人关节减速等工况场合的瓶颈问题．问题的难点大致有2个：①该机构是以具有2级减速装置和曲柄轴采用了中心圆盘支承结构为主要特征的封闭式组合行星传动机构，由于曲柄轴同时作为第2级摆线行星传动的输入与输出，因而曲柄轴及其附属结构上的误差对机构输出误差的影响复杂；②输出盘与行星架固连，输出误差也会伴随运动反馈至第1级行星齿轮传动中，反馈误差与构件的几何误差存在耦合．

早期Blanche等[1-2]与日高照晃等[3-5]分别采用几何与质量弹簧等价模型的方法，系统开展了RV减速器的误差分析与实验研究，揭示出影响其传动精度的主要因素，得出有益于提高系统传动精度的结论．之后，国内相关学者从20世纪90年代开始也围绕该种传动装置的精度分析与设计问题开展了相关研究.如文献[6]介绍了齿轮副整体误差的获得方法，文献[7-8]采用几何法建立了忽略行星传动一级误差影响的精度分析模型；文献[9]采用与日高照晃等[3-5]相类似的方法，构建了系统动态传动精度非线性动力学计算与分析模型；文献[10]结合虚拟样机技术，通过多刚体动力学仿真分析，研究了各原始误差对RV减速器动态转角误差的影响规律．然而，上述文献在针对RV传动机构的传动特点、体现误差传递过程以及反馈误差等方面存在不足．

笔者针对以上研究情况，为了能够明确揭示各原始误差因素在机构整个传动过程中对输出转角的影响规律，通过系统分析RV减速器的结构与传动特点，基于作用线增量法，推导了该类机构的误差传递矩阵，并在考虑机构的反馈误差与各构件几何误差耦合的基础上，建立了该机构的回转传动误差分析模型，为该类机构的精度分析与设计提供了可靠的理论依据．

1 机构的结构与传动特点

RV减速器是由行星齿轮与行星摆线组成的两级大速比减速传动机构，其机构简图如图1所示．机构中第1级行星齿轮传动为RV传动的差动机构，而第2级K-H-V型摆线行星传动为其封闭机构，其传动特点是中心轮1作为输入，传给行星轮2，进行第2级减速．行星轮2与曲柄轴3固连，将行星轮2的旋转运动通过曲柄轴3传给摆线轮4，构成摆线行星传动的平行四边形输入，使摆线轮4产生偏心运动．同时摆线轮4与针轮5啮合产生绕其回转中心自转运动，此运动又通过曲柄轴3传递给输出盘6实现等速输出转动．由于输出盘6也作为第1级行星齿轮传动的行星架，因此输出盘6的运动也将通过曲柄轴3反馈给第1级差动机构形成运动封闭．这种闭环机构提高了整机刚度[10]．

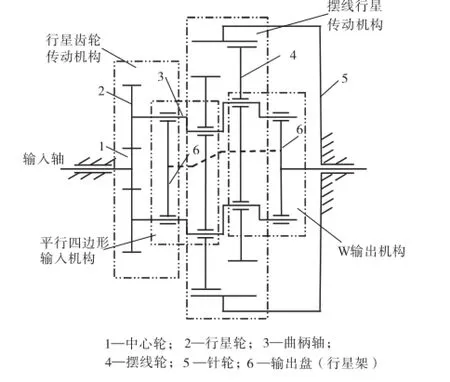
图1 RV传动机构示意Fig.1 Schematic of RV transmission mechanism

根据上述分析可知，RV传动机构中包含行星齿轮传动、平行四边形输入、摆线行星传动以及W输出4个子机构．

2 机构误差分析模型

2.1 系统描述与坐标系建立

为了系统研究构件原始误差对机构回转传动精度的影响，首先，针对机构的传动特点，分析机构中力的作用和运动的传递过程[11]，确定机构的作用线与运动线，建立各子机构的误差传递矩阵，构造原始误差因素与机构输出转角误差的映射关系；其次，考虑反馈误差与构件原始误差的耦合，推导它们对传动精度的综合影响．基于上述思想，建立坐标系对机构误差进行分析．坐标系如图2所示．

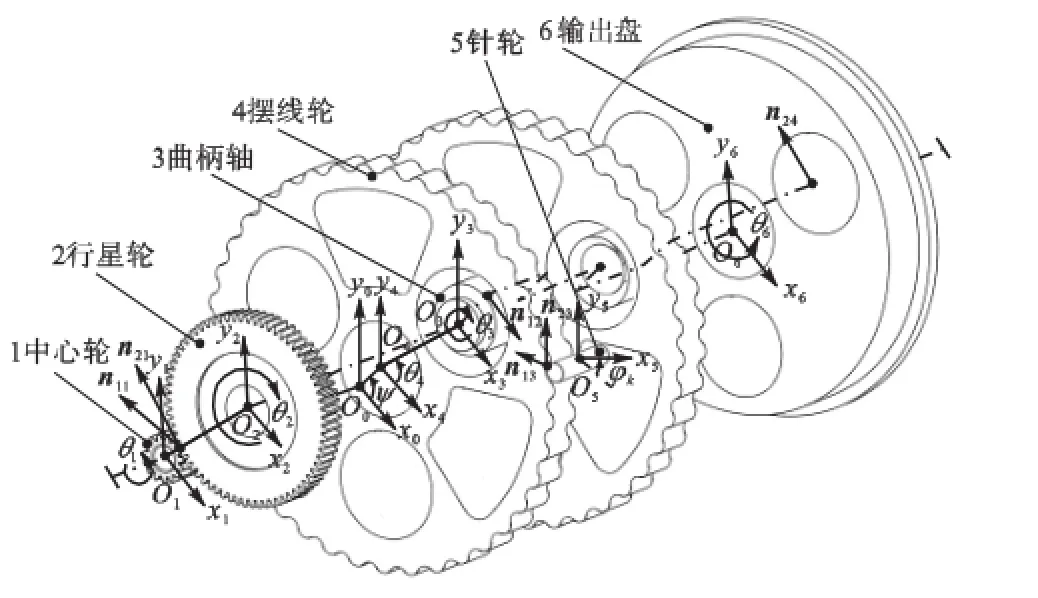
图2 坐标系Fig.2 Coordinate system

图2 中：O0为针轮中心圆的几何中心，固定坐标系O0x0y0位于与中心轮轴线垂直的平面上，并且与针轮固连；Oi为构件i自转中心，动坐标系Oixiyi与构件i固连，且在起始位置时轴xi与轴x0一致；θi表示各构件自转角度，逆时针方向为转角的正方向；ψ表示摆线轮偏心方向的初始值；φk表示针齿的位置，针齿的序号k以逆时针方向为正向，第1号针齿位于坐标轴x0正向上(zp为针齿个数)；n1J表示子机构J( J=1,2,3,4)的作用力方位即作用线；n2J表示子机构J中从动件上参考点瞬时运动轨迹的切线即从动件的运动线．2.2 各子机构误差分析模型

根据上述坐标系定义及对作用线和运动线在系统中的描述，在机构运动过程中，确定各子机构误差分析模型．由于机构原始误差所引起的作用都必须同作用线结合形成作用误差，而每个作用误差又必须与最后一个从动件的输出误差结合起来形成折合误差，即首先将原始误差投影到作用线上得到作用误差，再将作用误差反投影到运动线上得到折合误差[11].因此设子机构J上构件i原始误差为δJi，则子机构从动件的转角误差在固定坐标系O0x0y0中的表达式为

式中EJ为子机构J的误差传递矩阵[11]．式(2)即为RV传动机构中各子机构精度分析的一般表达式．2.2.1 行星齿轮传动误差分析

设中心轮转过任意转角θ1时各构件相对位置如图3所示，其中行星轮的自转运动为机构的输出，两齿轮的啮合点为运动参考点．作用线n11为两啮合齿廓的公法线，运动线n21为两啮合齿轮节圆的公切线，则n11、n21在固定坐标系O0x0y0下的表达式为

将式(3)代入式(1)中得行星轮自转角误差为

图3 行星传动机构Fig.3 Planetary transmission mechanism

2.2.2 平行四边形输入机构误差分析

图4为将行星轮的旋转运动传给曲柄轴后，曲柄轴转过θ3时各构件相对位置．根据机构受力分析可知，曲柄轴用于驱动摆线轮公转的作用力方位，即为平行四边形输入机构的作用线n12，垂直于曲柄轴的偏心方向，且此时从动件摆线轮公转的运动线n22与作用线n12方向一致．n12、n22在固定坐标系O0x0y0下的表达式为

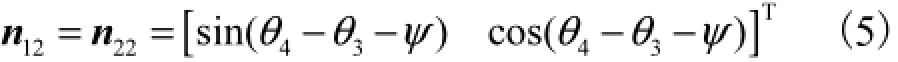
同理将式(5)代入式(1)得到平行四边形输入机构中摆线轮公转的转角误差为

图4 平行四边形输入机构Fig.4 Parallelogram input mechanism

2.2.3 摆线行星传动误差分析

由于摆线轮上n个均布且同姿的曲柄运动可用输出圆盘中心的一个虚拟曲柄轴等效，因此，可建立对应的摆线行星传动机构运动简图，如图5所示．图5中偏心量04O O与曲柄轴的偏心量一致，其大小为a，pr为针齿中心圆半径．

图5 摆线行星传动机构Fig.5 Cycloidal planetary transmission mechanism

任意时刻，针对一个针齿与摆线轮啮合进行分析，选取针齿与摆线轮的啮合点为参考点，啮合点处的作用力方位即为针齿对摆线轮的作用线n13，其方向沿摆线轮理论廓线的法向，而啮合点相对于摆线轮中心的速度方向即为运动线n23，其方向垂直于啮合点处的摆线轮矢径．在固定坐标系O0x0y0下n13、n23的表达式为

2.2.4 W输出机构误差分析

从运动关系来看，W输出机构与平行四边形输入机构相同，其运动简图如图6所示．图中输出盘的运动线24n，沿输出盘的切线方向，作用线14n垂直于相应的运动矢径，即14n、24n方向一致．则在固定坐标系下14n、24n的表达式为

将式(9)代入式(1)中得到该子机构中输出盘的转角误差为

图6 W输出机构Fig.6 W-output mechanism

为了得到子机构J中构件i的原始误差δJi引起的机构输出盘的转角误差，利用误差传递矩阵求出第J个子机构的从动件转角误差同时也是第J+1个子机构主动件的转角误差，然后用同样的方法求出J+1个子机构从动件的转角误差，依次一直进行下去即可求出最后要求的机构输出转角误差．

由于行星齿轮传动机构与输入平行四边形机构在传动过程中需经过第2级摆线针轮的减速传动，因此δJi引起RV传动机构输出盘转角误差也要缩小相当于摆线针轮的传动比i倍，即为

由第1节对机构结构及传动特点的分析可知，机构输出盘的运动通过与之固联的行星架反馈到第1级的行星齿轮传动中，实现机构运动的封闭．根据误差传递的实质，输出盘的转角误差τΔ也会伴随运动一起反馈到第1级中，其直接影响是造成了行星轮的中心位置误差，记为fδ，其矢量表达为为太阳轮、行星轮的分度圆半径)．在考虑反馈误差的情况下，可得机构的输出盘的总的转角误差为

式中：Δτ1′4由2部分组成，一是行星齿轮传动中各构件原始误差引起的输出转角误差，二是反馈误差引起的输出转角误差，即

对式(12)变形可得

式(14)即为考虑反馈误差与构件原始误差耦合所引起的机构输出盘综合转角误差．

3 算 例

为验证以上误差分析模型的有效性，以RV320S型减速器为例，研究各构件原始误差因素对输出盘转角误差的影响规律．该型号减速器的几何参数如表1所示．

表1 RV320S型减速器几何参数Tab.1 Geometrical parameters of RV320S reducer

分别在4个子机构中各选取一个原始误差因素作为研究对象．设机构中存在行星轮偏心误差为偏心位置初始角，且初始角为随机量)，曲柄轴偏心误差摆线轮齿廓误差以及输出盘上曲柄轴孔偏心误差根据式(11)可以计算出各原始误差因素对机构输出转角的影响系数，得到它们在机构运动过程中对机构输出转角误差的影响规律，如图7所示．

图7 输出误差影响系数Fig.7 Error index of output

图7 的横坐标为机构的输出转角，从图中可以明显看出，对机构输出转角误差影响最大的是输出盘上曲柄轴孔偏心误差，此误差完全反映到输出，在设计时要特别注意．其次是摆线轮齿廓误差，此误差在摆线轮自转一周时呈余弦周期分布，因此若能保证2个摆线轮按标准相差180°来安装，则可以使2个摆线轮在同一个方向上的误差相互抵消．

选取文献[7]中构件原始误差参数值如表2所示．将表1和表2参数代入式(14)，可以得到反馈误差与各子机构上原始误差Jiδ耦合引起的机构综合输出转角误差，如图8所示．

表2 构件几何误差Tab.2 Geometrical errors of components mm

图8 输出转角误差Fig.8 Angular error of output

图8 (a)主要反映了反馈误差对机构输出转角的影响情况，其横坐标为机构的输入转角．可以发现，是否考虑反馈误差对计算机构综合输出转角误差存在一定的偏差，这对于进一步开发研制该类精密传动机构是不容忽视的．图8(b)反映了在考虑反馈与表2所示误差耦合作用时引起的机构综合输出转角误差，其横坐标为机构的输出转角．

4 结 论

(1)通过作用线与运动线分析，揭示出机构中共用构件曲柄轴的误差传递过程．当曲柄轴作为第2级摆线行星传动输入时其误差传递沿垂直于曲柄轴的偏心方向，而作为输出时则与输出盘的运动矢径方向垂直．

(2)将机构反馈误差等效为行星轮的中心位置误差，通过求解输出盘的总的转角误差，可得到反馈误差与构件几何误差的耦合关系，为此类机构的精度分析与设计提供可靠的理论依据．

(3)各种原始误差中对机构输出转角误差影响最大的是输出盘上曲柄轴孔的偏心误差，其次是摆线轮齿廓误差；值得注意的是反馈误差对于高精密RV传动系统的影响也应重视．

［1］ Blanche J G，Yang D C H. Cycloid drives with machining tolerances[J]. Journal of Mechanical Design，1989，111(3)：337-344.

［2］ Yang D C H，Blanche J G. Design and application guidelines for cycloid drives with machining tolerances[J]. Mechanism and Machine Theory，1990，25(5)：487-501.

［3］ 日高照晃，王宏猷，石田武，齿车を用K-H-V形遊星齿车装置の回転传达误差研究(第1报，解析方法)[J]. 日本机械学会论文集：C编，1994，60(570)：645-653.

Hidaka T，Wang H，Ishida T，et al. Rotational transmission error of K-H-V planetary gears with cycloid gear (1st report, analytical method of the rotational transmission error)[J]. JSME International Journal：Series C，1994，60(570)：645-653(in Japanese).

［4］ 石田武，王宏猷，日高照晃，齿K-H-V形遊星齿车装置回転传达误差研究(第2报，各种加工误差·组立误差が回転传达误差J]. 日本机械学会论文集：C编，1994，60(578)：278-285.

Ishida T，Wang H，Hidaka T，et al . Rotational transmission error of K-H-V planetary gears with cycloid gear (2nd report，effects of manufacturing and assembly errors on rotational transmission error)[J]. JSME International Journal：Series C，1994，60(578)：278-285(in Japanese).

［5］ 王宏猷，石田武，日高照晃K-H-V形遊星齿车装置回転传达误差研究(第3报, 各种误差相互影响)[J]. 日本机械学会论文集：C编，1994，60 (578)：286-293.

Wang H，Ishida T，Hidaka T，et al . Rotational transmission error of K-H-V planetary gears with cycloid gear (3rd，mutual effects of errors of the elements on the rotational transmission error)[J]. JSME International Journal：Series C，1994，60(578)：286-293(in Japanese).

［6］ 石照耀，康 焱. 齿轮副整体误差及其获取方法[J].天津大学学报，2012，45(2)：128-134.

Shi Zhaoyao，Kang Yan. Gear pair integrated error and its measurement method[J]. Journal of Tianjin University，2012，45(2)：128-134(in Chinese).

［7］ 何卫东. 机器人用高精度RV传动的研究[D]. 哈尔滨：哈尔滨工业大学机电工程学院，1999.

He Weidong. The Analysis Research of High Accurate RV Transmission[D]. Harbin：School of Mechatronics Engineering，Harbin Institute Technology，1999(in Chinese).

［8］ 李充宁，刘继岩，孙 涛. 2K-V型行星传动中摆线针轮啮合的传动精度研究[J]. 机械工程学报，2001，37(4)：62-65.

Li Chongning，Liu Jiyan，Sun Tao. Study on transmission precision of cycloidal pin gear in 2K-V planetary drives[J]. Chinese Journal of Mechanical Engineering，2001，37(4)：62-65(in Chinese).

［9］ 韩林山，沈允文，董海军，等. 2K-V型传动装置动态传动精度理论研究[J]. 机械工程学报，2007，43(6)：81-86.

Han Linshan，Shen Yunwen，Dong Haijun，et al. Theoretical research on dynamic transmission accuracy for 2K-V-type drive[J]. Chinese Journal of Mechanical Engineering，2007，43(6)：81-86(in Chinese).

［10］ 朱 斌，秦 伟，孙 伟，等. 2K-V型摆线针轮减速器的动态回转传动误差分析[J]. 机械传动，2011，35(4)：12-15.

Zhu Bin，Qin Wei，Sun Wei，et al. Dynamic revolution and transimission error analysis of 2K-V cycloidalpin planetary gear speed reducer[J]. Journal of Mechanical Transmission，2011，35(4)：12-15(in Chinese).

［11］ 杨玉虎，洪振宇，张 策. 机构位置误差分析的传递矩阵法[J]. 机械工程学报，2005，41(2)：20-23.

Yang Yuhu，Hong Zhenyu，Zhang Ce. Transfering matrix method for precision analysis of mechanism[J]. Chinese Journal of Mechanical Engineering，2005，41(2)：20-23(in Chinese).

Precision Analysis of RV Transmission Mechanism

Yang Yuhu1，Zhang Jie1，Xu Lixin2
(1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300072，China；2. School of Mechanical Engineering，Tianjin University of Technology and Education，Tianjin 300222，China)

In this paper, a two closed planetary transmission mechanism, the rotate vector (RV) mechanism, which consists of involute gears and cycloidal gear is taken as a research object. Based on the incremental principle of the force action line, the effect of the original errors of components throughout the transmission process on the output angular error of mechanism is analyzed by using error transferring matrix. An applicable error model is established for the mechanism error analysis. This model presents the analytical corresponding relationship between the original errors of components and the mechanism output error. Furthermore, the error transfer process of the common components such as the crank shaft and the coupling relationship between the feedback-error and geometric errors caused by fixing the output tray and the tie bar is revealed, which offers a reliable theory in precision analysis and mechanism design. Finally, the RV320S reducer is used as an example to illustrate the effectiveness of this model. The results indicate that the most influential factor for the output error is the eccentric error of the crank shaft hole on the output disk, followed by the error of cycloid tooth profile; that the feedback-error is a remarkable factor for machining high precision RV transmission mechanism.

rotate vector(RV) transmission mechanism；error analysis model；feedback-error；errors transferring matrix

TH132

A

0493-2137(2013)07-0623-06

DOI 10.11784/tdxb20130709

2012-01-01；

2012-05-15.

国家高技术研究发展计划(863计划)资助项目(2011AA04A102)．

杨玉虎（1962— ），男，博士，教授.

杨玉虎，yangyuhu@tju.edu.cn.