“1∞”型极限计算方法的探讨

贺 欣，张 媛

(郑州铁路职业技术学院，河南 郑州 450052)

不定式极限是函数极限教学的重点和难点，许多不定式极限常常需要通过一系列颇具技巧的恒等变形才能计算出来.由于不同的题目需要不同的变形技巧，缺乏规律性，不易掌握.本文利用变量替换法，针对“1∞”型极限，给出了一个较为简洁规范的方法，从而省去了繁琐的变形，便于实际应用.

1 不定式极限的定义及解法介绍

本文重点讨论方法2的应用.

利用恒等变形计算如下

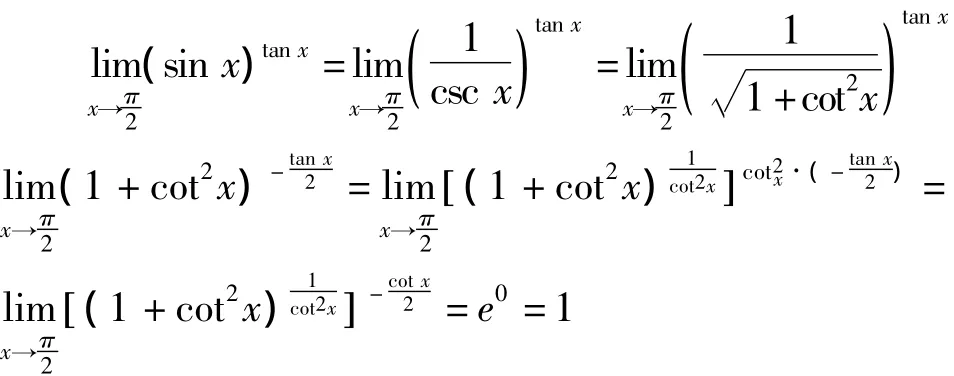
这样，找到一个更为通用易学的方法对初学者来说就很重要了，它不仅有助于解题，更有助于帮助初学者从繁琐的变换中解放出来，将精力集中在对极限的掌握中，更好地理解重要极限的本质.下面介绍的变量替换法就可以达到这一目标.此方法的原理是:

⑵其中α→0，即α是x→0时的无穷小量.

因此首先必须将底数f(x)化为(1+α)的形式，即做变量替换f(x)=1+t，此时f(x)g(x)=(1+t)g(x)=，因为，从而 t→0，由于极限，所以只需计算出－1·g(x)］的极限即可.若(x)－1］·g(x)}=A，则

2 应用举例

下面我们通过实例来说明变量替换法的应用.

解:令 sin x=1+t，则 t=sin x －1，所以时，t→0－，有

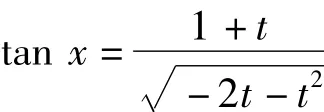
我们再来看两个例子.

解:令1，当 x→0 时，t→0，从而

又因为

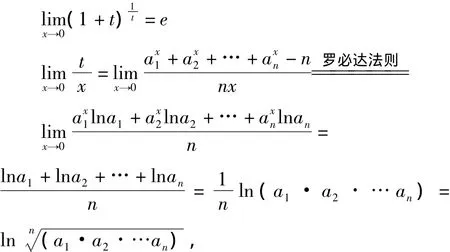
所以

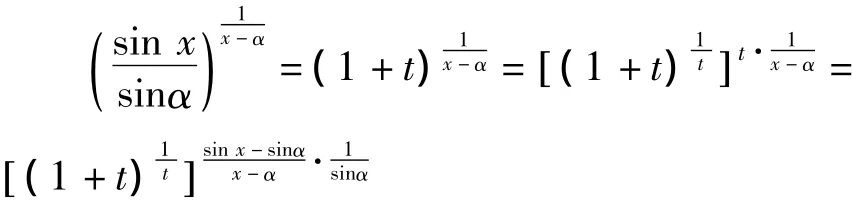
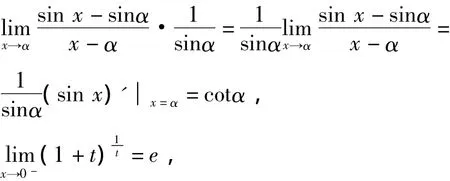
3 补充说明

(1)本文是以方法2为重点讨论的，事实上本文中的例1和例3应用方法1去计算，也非常简洁，不再赘述;

(2)有时，有些“1∞”型极限，用简单的恒等变形计算来得更加简单，如

从而

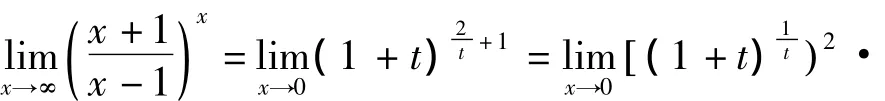
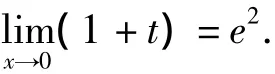
依然可行，但稍显复杂.

通过上面的三个例子发现，尽管我们遇到的实际问题经常不同，利用变量替换法求解“1∞”型极限时，由于其具有规律性，便于操作，避免了不同题目用不同的解法，难于寻找思路的困惑，同时也避开了繁琐的恒等变形，使得计算变得更加简洁，不失为一种简单高效的计算方法.

吉米多维奇.数学分析习题集［M］.北京:人民教育出版社，1958.