地铁列车吸能装置吸能原理的仿真研究

李建龙，高 伟

(郑州铁路职业技术学院，河南 郑州 450052)

0 引言

现代城市轨道交通由于其客运量大、快速、便捷、准点等特点而越来越受到青睐。我国的城市轨道交通起步虽晚，但近年来发展迅猛。除了一些特大城市，许多省市级大中等城市以不同的形式开始了城市轨道交通建设。尽管地铁列车在专有的轨道上运行，发生碰撞事故的可能性要远小于其他交通运输工具。然而，由于地铁列车质量大，速度较高，又主要运行在人口密度较高的市区，且载客量大，若发生碰撞事故会造成严重的人员伤亡和财产损失。因此，如何提高地铁列车在碰撞事故中的被动安全性就成为一个不可忽视的重要问题。这就需要设计专用吸能装置来吸收碰撞发生时列车的动能。本文提出一种新的碰撞能量耗散原理，即发生列车碰撞时，薄壁金属构件被刀具轴向切割，从而吸收列车的动能，降低列车的减速度。由于轴向切割薄壁金属构件时，其吸能特性与刀具的数量、构件的壁厚、外径等因素密切相关，因此本文将从这几个方面进行讨论，找出薄壁结构被轴向切割时的吸能规律。

1 动态仿真显式有限元

随着计算机技术与有限元理论的发展，有限元技术已经成为研究金属切割过程的一个重要手段。显式时间积分适用于各种结构冲击动力学问题，如爆炸、碰撞和金属加工成型等高度非线性问题，它采用中心差分时间积分，其基本特点是不形成总体刚度矩阵，弹性项放在内力中，避免了矩阵求逆。这对非线性分析很重要，无须检查收敛，是条件稳定的。金属切割具有动态性、大变形和高度非线性的特点。因此运用显式有限元程序对这一过程进行分析模拟非常适合。本文采用通用的非线性显式动力分析程序LS－DYNA仿真薄壁结构的切割吸能过程。

2 薄壁结构材料动态塑性本构关系

选择合适的材料模型是准确模拟切割过程的关键。本文选用LS－DYNA材料库中的塑性随动应变率相关材料模型模拟薄壁结构。该模型考虑了应变率对材料屈服应力的影响。其屈服应力的计算如下:

3 显式有限元分析模型的建立

刀具采用硬质合金，其硬度、强度远大于薄壁构件。用钢体模拟，薄壁构件材料为1018钢，横截面为圆形，管长300mm。本文分别模拟了不同壁厚、不同外径的薄壁结构被不同数量的刀具切割时的吸能特性。

薄壁结构一端固定，另一端被刀具以恒定的速度沿轴向切割。薄壁结构的材料类型为随动塑性材料(Plastic Kinematic)。单元类型全部为单点积分实体单元。有限元模型如图1所示，(a)、(b)、(c)、(d)依次为二、四、六、八个刀具切割薄壁结构的有限元模型。

图1 薄壁结构切割吸能的有限元模型

4 数值模拟结果及分析

4.1 薄壁结构吸能特性与刀具数量的关系

壁厚6mm，管长300mm、外径100mm，刀具数量分别为2、4、6、8个时，薄壁结构吸收的能量如图2所示，界面力－时间历程如图3所示。

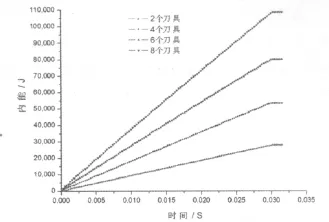
图2 刀具数量不同时的内能－时间历程图

图3 刀具数量不同时的界面力－时间历程图

薄壁结构的吸能特性与刀具数量的关系如表1所示。

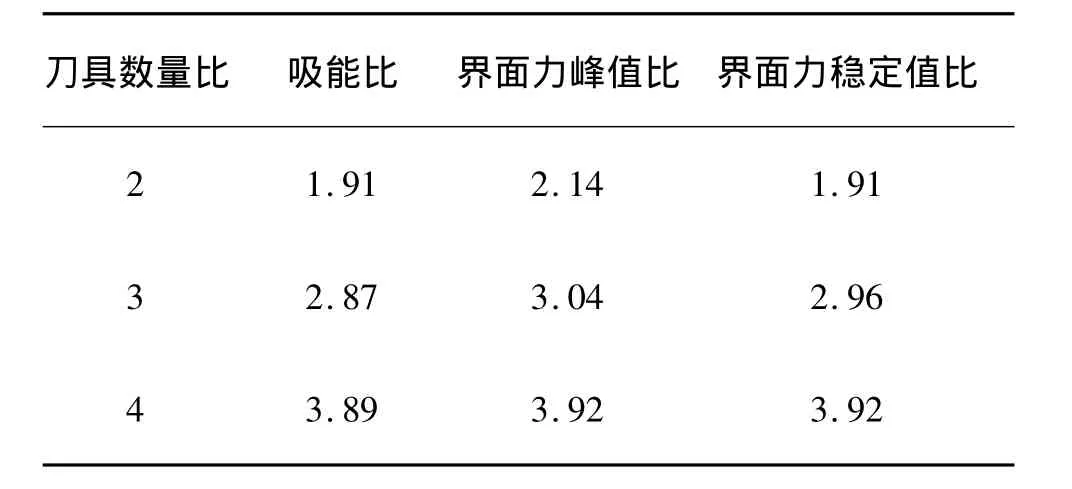
表1 薄壁结构的吸能特性与刀具数量的关系

由表1可知，在壁厚、外径、长度相同的条件下，薄壁结构吸收的能量、界面力峰值、界面力稳定值都与刀具的数量成正比。并且，刀具数量不同时，薄壁结构吸收的能量比、界面力峰值比、界面力稳定值比都近似等于刀具数量的比值。

4.2 薄壁结构吸收的能量与壁厚之间的关系

刀具为2个，外径100mm、管长300mm、壁厚分别为6mm、8mm、10mm时，薄壁结构吸收的能量如图4所示，界面力－时间历程如图5所示。

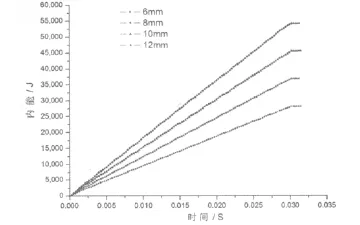
图4 壁厚不同时的内能－时间历程图

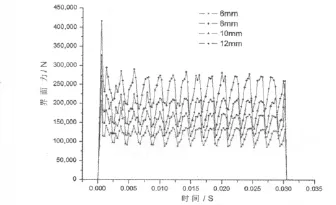
图5 壁厚不同时的界面力－时间历程图

薄壁结构的吸能特性与壁厚的关系如表2所示。

表2 薄壁结构的吸能特性与壁厚的关系

由表2可知，在管长、外径、刀具数量相同的条件下，薄壁结构吸收的能量大小、界面力的峰值和稳定值都与壁厚成正比。并且，壁厚不同时，薄壁结构吸收的能量比、界面力峰值比、稳定值比都近似等于壁厚的比值。

4.3 薄壁结构吸收的能量与内径之间的关系

壁厚为6mm，刀具为2个，管长300mm，内径分别为50mm、100mm时，薄壁结构吸收的能量如图6所示，界面力－时间历程如图7所示。

图6 壁厚不同时的内能－时间历程图

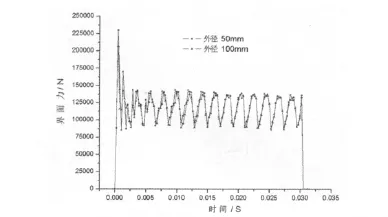
图7 壁厚不同时的界面力－时间历程图

从图6、图7可以看出，相同条件下，不同外径的薄壁结构吸收的能量、界面力峰值和稳定值基本相同。

5 结论

综合以上分析，可以得出以下结论:

薄壁结构轴向切割吸能过程中吸收的能量、界面力与刀具的数量、薄壁结构的壁厚成正比，与薄壁结构的外径关系不大。

［1］Wierzbichki T，Abramowicz W.On the crushing mechanics of thin － walled structure［J］.J.of Applied Mechanics，1983，50:727－734.

［2］Ted Belytschko，Wing Kam Liu，Brian Moran.连续体和结构的非线性有限元［M］.庄茁，译.北京:清华大学出版社，2002.

［3］Soo SL，Aspinwall D K，Dewes R C.3D FE modeling of the cutting of Inconel 718［J］.Journal of Materials Processing Technology，2004，105:116 －123.

［4］钟志华，张维刚，曹立波，等.汽车碰撞安全技术［M］.北京:机械工业出版社，2003:42－58.

［5］单其雨，肖守讷，阳光武.新型吸能装置的耐撞性分析［J］.机车电传动，2010(2):12 －15.

［6］王文斌，康康，赵洪伦.列车耐碰撞系统有限元和多体动力学联合仿真［J］.同济大学学报(自然科学版)，2011，39(10):1552－1556.