二级直齿轮减速器设计研究

李 锐，邓清卫

(郑州铁路职业技术学院，河南 郑州 450052)

目前，行星齿轮的传动技术已经被广泛地应用到机械设计过程当中，特别是那些对于体积和质量的要求较小、结构要求相对紧凑但是传递效率却要求很高的航空机械、矿山机械、起重运输机械、石油化工机械等方面的应用。在应用过程当中，以质量、体积、承载能力为代表的要素是衡量行星减速器整体性能好坏的核心指标，这三种要素的性能在很大程度上取决于传动参数的选择。为了尽可能地减小行星减速器的质量和体积，节省材料，全面提高承载能力，最终获得最佳的设计参数，科学地提高机器的性价比，必须要采用相对优化的设计方法。

1 减速器设计变量的确定

行星减速器主要是由两个2K－H型的部件串联组成了一个2级减速的传动装置，详情见图1。太阳轮1(与电机联接)是作为输入轴而存在的，行星架H1则是作为第1级的减速传动的输出轴而存在的，同时也是第2级减速传动(与太阳轮3相联接)的输入轴装置，而另外的行星架H2则是作为减速器的输出轴(与负载机构联接)而存在的。

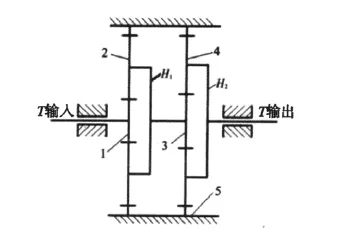
图1 机构传动简图

对于行星减速器而言，如果按照既定参数输入了功率P、总传动比i0、转速n以及行星轮的个数np之后，那么其整个体积的大小在很大程度上取决于齿轮的m、z、b、x等几个参数的变化。本文当中所涉及到的齿轮的m都是一样的，齿轮的z、x的对应值则有5个左右，但它们并不都是相对来讲较为独立的变量，而是在一定情况下会受到配齿条件以及相应的总传动比的制约而产生变化的。所以对于某一齿数z1以及某一变位系数x1而言，只能存在着一组齿数方案以及相应的变位系数方案，所以最终我们确定设计变量定为:

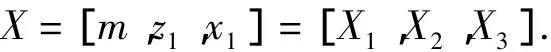
2 减速器目标函数的建立

在最终确定行星减速器齿轮材料的时候，为了全面地实现节省空间、节约材料、便于安装以及降低制造成本等多方面的需求，通常都是以行星减速器的体积作为最终的设计准则来执行的，在此过程中还要注意使之保持最小的状态。同时为了使得齿顶的高系数ha*以及相应的变位系数x等参数都能够满足之前所制定的约束条件，就需要在相应的目标函数中反映出上述参数。因此，太阳轮以及行星轮齿的顶圆直径通常都是用来计算体积的，内齿轮同样也是按照齿根圆直径平方最终减去齿顶圆直径平方的方式来计算相应的体积的。故可以表现为以下内容:

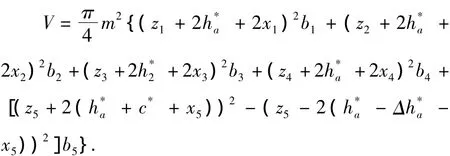
式中:b1、b2、b3、b4、b5分别表示 1、2、3、4、5 齿轮的齿宽;x1、x2、x3、x4、x5分别表示 1、2、3、4、5 齿轮的变位系数;C*表示顶隙系数;Δh*a表示齿高变动系数。

3 减速器约束条件的建立

根据行星齿轮实现传动的整体设计要求，必须要将各项约束内容逐渐地分为强度约束条件、配齿约束条件以及相应的其他方面的约束条件。

3.1 配齿方面的约束条件

(1)传动比条件:

(2)同心条件:

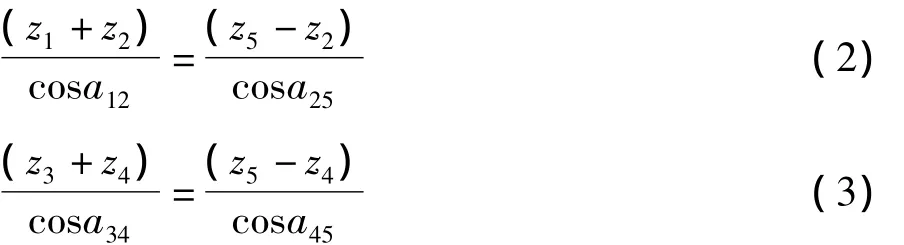
式中:cosa'12、cosa'25、cosa'34、cosa'45分别是 1 － 2、2－5、3－4、4－5齿轮副的实际啮合角。

(3)邻接条件:

式中:da2、da4分别为2、4 齿轮的顶圆直径;a'12、a'34分别是1－2、3－4齿轮副的实际中心距。

(4)安装条件:

式中:np1、np2分别为一级、二级传动中行星轮的个数。

3.2 强度方面的约束设计

在行星减速器的设计过程中，一旦发现了太阳轮同行星轮的材料一致的情况时，只要太阳轮的整体强度可以满足上述的基本条件，那么行星轮同内齿轮的强度也就一定会满足相应的条件，所以只能将太阳轮强度当作是强度约束条件而实现。

3.2.1 齿面接触强度:

3.2.2 其他方面的约束条件

(1)模数限制:齿轮用于传动动力和转矩，需取

(2)齿宽限制:根据齿宽与模数之间的关系确定齿宽的约束条件。

(3)啮合角限制:用于外啮合的齿轮，常用大啮合角

用于内啮合的齿轮，接触面当量曲率较大，齿根弯曲强度较高，其啮合角需降低为:

(4)行星轮个数限制:取行星轮个数为:

4 减速器优化的实现方法

在上述优化设计的过程中，主要包含了3个设计变量、1个目标函数以及相对应的17个约束条件的存在，属于用有多个离散设计变量、不等式约束以及连续设计变量所构成的单目标函数来实现优化设计方面的问题。它的整体求解一定要采用离散变量的优化方法来实现，如果仅仅采用搜索形的离散变量优化方法，会很难确认全局可以获得的最终的最优解，所以建议可以采用混合离散变量的优化方式来确定最终的设计方法。

混合离散变量的优化设计方法具体指的是首先要以离散复合形作为存在的基础，然后通过对于有效目标函数的利用以及其他方面的约束条件进行相应的约束，最终实现按照一维离散的搜索以及用重新启动技术作为相应的算法来实现相应的主体功能。但是为了尽可能地适应实际问题中所遇到的数学模型的复杂性，还可以进一步加强针对贴边技术、加速措施以及重构领域查点等辅助功能的深入，最终以便于形成一个相对完整的混合离散复合形算法。综合来讲，其基本思想可以总结为:首先是保证要在满足约束条件的空间内最终产生出相应的k(n+1≤k≤2n)个初始离散点，然后主要将这些离散点逐渐地组合成初始的复合形;接下来再根据复合形各顶点函数值的大小情况来最终确定函数值的下降方向，最终可以使得复合形持续不断地向最优解方面实现收缩，直到满足一定情况下的收敛条件才算结束。具体步骤可以表示如下:

(1)重点针对连续变量x1以及其所对应的非均匀离散变量m之间进行均匀的离散化处理，使它们都可以逐渐地转化成为均匀的离散变量而存在。

(2)针对具体情况确定一个固定的初始离散点X(0)，使其它的三个分量都可以满足变量值对于边界条件的要求，同时还要根据针对初始离散复合形顶点所制定的相应的计算公式的计算，最终可以得到2n+1个顶点的数值，再依次截取前k(n+1≤k≤2n)个顶点的数值当做是初始离散点的开始位置，这样就可以实现在离散空间中初步形成初始离散复合形，方便以后工作的开展。

(3)在针对初始离散复合形各顶点所对应的目标函数值进行计算的时候，首先要确定顶点中的最坏点X(H)、最好点X(L)的位置，然后还要以最坏点X(H)作为相应的基点，以X(H)同其余的k－1个顶点作为几何中心点X(C)的连线方向开展搜索方向S的最终确定，同时还可以以X(C)以及X(H)之间的连线长度同步长因子a之间的乘积作为整体步长的确定来源，最终保证进行离散一维搜索过程的开展，便可以得到新离散点X(T)。

［1］陈照军，徐爱娟，陈满红，等.十吨级双级减速桥轮边减速系统的匹配设计［J］.安徽科技，2010(7):12.

［2］张春生，马国新.履带车辆电磁悬挂增速机构的研究［J］.车辆与动力技术，2007(3):28.

［3］李洪武，胡培林，陈艳清.以提高轴承寿命为目的的行星排中心论位置的优化设计［J］.车辆与动力技术，2010(3):36.

［4］黄宏成，闻居博.功率分流CVT方案分析［J］.传动技术，2009(2):19.

［5］桂乃磐，郭惠昕，罗佑新.用J特性图计算封闭差动轮系传动比的原理与方法［J］.湖南文理学院学报(自然科学版)，2004(3):23.

［6］王德伦，张石静，许南绍，等.电动汽车行星齿轮式无级变速器建模与仿真［J］.重庆理工大学学报(自然科学版)，2010(11):33.