氢氧加湿燃烧过程一维数值仿真
2013-05-28高育科韩新波李洪伟万荣华
高育科, 彭 博, 胡 巍, 韩新波, 李洪伟, 万荣华
氢氧加湿燃烧过程一维数值仿真
高育科, 彭 博, 胡 巍, 韩新波, 李洪伟, 万荣华
(中国船舶重工集团公司 第705研究所, 陕西 西安, 710075)
针对氢氧燃烧中间加湿过程, 建立了燃烧掺混及水蒸气流中冷却水液滴蒸发的数学模型, 采用欧拉-拉格朗日方法对燃烧器中氢氧加湿燃烧及冷却水喷雾蒸发过程进行了一维(1D)数值仿真, 得到了燃烧器内蒸汽压力、温度等物理量分布及冷却水液滴的运动变化过程, 并针对含湿量不同的氢氧入口条件及冷却水工况进行了计算, 分析了各参数变化对掺混燃烧过程的影响, 为氢氧加湿燃烧过程分析和燃烧室的初步设计提供参考。
氢氧加湿燃烧; 数值仿真; 燃烧器; 喷雾
0 引言
以氢氧为燃料的燃烧室中氢氧燃烧产生高温高压燃气, 为了运行安全和得到符合要求的输出蒸汽工质, 常通过喷入冷却水来保护燃烧室和调节输出工质参数, 另外在某些应用领域, 氢氧进入燃烧室时可能含有一定湿度, 所以其中的过程涉及一定湿度条件下的含湿氢氧射流燃烧、蒸汽流中冷却水液滴蒸发等过程。本文通过对氢氧加湿燃烧过程和蒸汽流中冷却水液滴的运动变化过程的分析, 建立了氢氧加湿燃烧的气相流动和液滴运动变化过程的数学物理模型, 采用simple算法进行气相燃烧流动计算, 基于轨道模型计算液相蒸发过程, 通过气液耦合, 计算得到燃烧器中各物理量分布及液滴运动变化过程, 并针对不同工况进行仿真计算, 研究各参数对掺混燃烧过程的影响。
1 工作原理
仿真针对的燃烧器构型如图1所示, 含湿氢氧射流进入燃烧器, 燃烧产生水蒸气流, 在燃烧后的蒸汽流中掺入冷却水喷雾进行掺混降温, 通过喷水不仅可以对燃烧室起到保护的作用, 而且可以通过调节喷水条件来调节输出工质的参数。
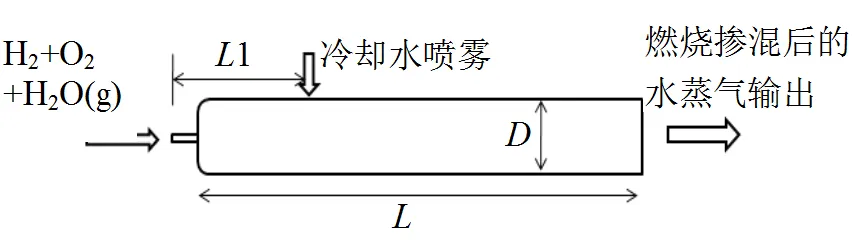
图1 氢氧加湿燃烧器构型
2 数学模型
氢氧燃烧掺混试验器中的过程涉及含湿氢氧的射流燃烧及冷却水喷雾的掺混蒸发等过程,燃烧器中气相数学模型由质量守恒、动量守恒、能量守恒方程构成, 液相数学模型由液滴的粒径、速度、温度变化方程构成, 通过对液滴各参量的计算, 得出液滴作用于气相的质量、动量、能量源项, 将上述源项引入气相各方程耦合求解, 得到燃烧器中含湿氢氧燃烧及与冷却水掺混过程的气液两相的完整解。
2.1 气相模型
质量守恒方程

动量守恒方程
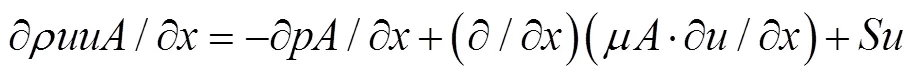
能量守恒方程[1]

其中,为总焓
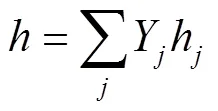

,,分别为液相作用于气相的质量、动量、能量源项[2], 定义为
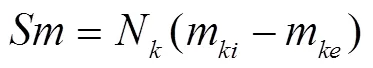
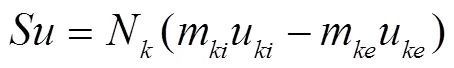

2.2 液相模型
液相计算采用轨道模型, 即在拉格朗日坐标系下考察液滴群沿各自轨道运动时的质量损失、动量变化和能量变化。计算中只考虑阻力且假设液滴温度均一。
1) 液滴的运动方程
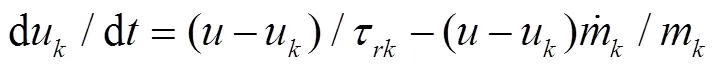

2) 液滴粒径变化方程
液滴初始加入时, 其温度低于环境压力下的饱和温度, 液滴表面由氢氧燃烧后的水蒸气包裹形成温度和浓度边界层, 温度边界层中液滴表面和饱和温度蒸汽界面之间的球壳区域内蒸汽处于未饱和状态会凝结, 而液滴表面蒸汽和蒸汽主流之间的浓度梯度会导致液滴扩散蒸发, 在凝结和蒸发共同作用下, 可以假定初始阶段液滴质量不变, 只有温度增加而无蒸发的过程, 当液滴达到饱和温度后, 液滴温度不变并开始蒸发。
a. 液滴未达到饱和温度时

b. 液滴达到饱和温度后
采用Ranz-Marshall关系式, 可得球形液滴平均数
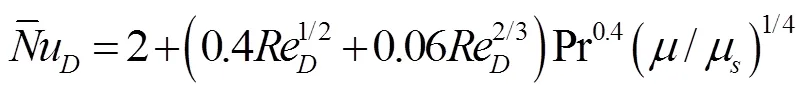
由的定义可得

由传热与传质的类比关系

可得
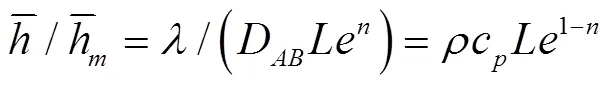
假设=1, 可得

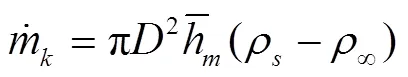
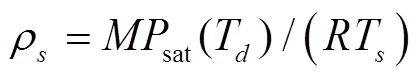
其中,T为饱和温度。
液滴质量为

综合各式, 得到液滴粒径平方的变化方程为

3) 液滴温度变化方程
当温度低于沸点时, 气相对液滴进行加热, 温度升高。温度变化方程为
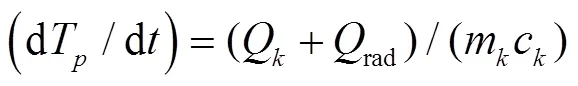

气相与液相之间的对流换热

气相和液相之间的辐射换热
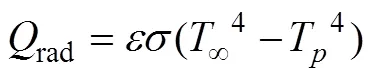
以上计算中, 物性参数随温度变化, 且边界层蒸汽物性参数,,,c依据1/3定律[4]计算。
4) 液滴尺寸分布
喷嘴喷雾液滴是连续分布的, 为进行数值计算,必须对连续分布的液滴进行离散化处理。假设液滴喷雾尺寸分布符合Rosin-Rammler分布, 将连续尺寸分布的液相按照该分布分成多个离散尺寸组, 每组用平均直径d表示。

3 数值解法
气相主方程组的求解基于simple算法[5], 采用交错网格, 分别引入速度、压力脉动值及温度松弛因子对各变量进行松弛迭代[6], 边界条件采用速度入口和压力出口, 利用TDMA算法求解各线性方程组。
采用4阶Runge-Kutta法[7]计算液滴速度、粒径和温度变化, 液滴轨道利用线性表达式计算[8]
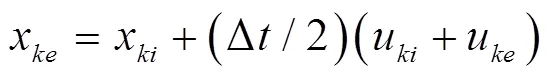
将拉格朗日坐标系下的液滴计算结果转化至气相欧拉坐标系下单元格内, 计算出源项加入到气相各方程。先利用simple算法解未加入掺混的气相各场, 待达到粗收敛时进行液相计算, 并在各气相方程中加入源项计算气相各场, 迭代若干次后, 重新计算液相参数, 并作为源项加入气相各方程计算, 如此反复多次直至收敛, 上述方法即利用单元内颗粒源(particle source in cell, PSIC)方法进行气液耦合计算[9]。1D计算程序流程如图2所示。

图2 氢氧加湿燃烧过程1D程序结构
4 计算结果及分析
利用文中建立的程序进行数值计算, 对化学恰当比燃料流量入口和压力出口条件下的氢氧掺混燃烧进行计算, 掺混冷却水垂直燃烧器轴线喷入主流。下文算例中, 掺混水流量变化时, 通过调整喷嘴参数使喷嘴的索特尔直径保持不变。
1) 含湿氢氧掺混燃烧(气相分布、液滴变化) 含湿氢氧燃烧且加入掺混水冷却的燃气温度分布如图3所示(文中图线涉及物理量轴向分布时, 轴向距离值均由轴向位移与总轴线长比值来表示), 同等条件下, 氢氧燃烧温度高达3 000~ 4 000 K, 入口燃料含一定湿度条件下氢氧燃烧后温度只达到1 460 K, 通过加入掺混水喷雾冷却温度降至1 000 K左右。由燃气速度分布图4可知, 气体经过燃烧器前导管时, 速度高达10~12 m/s且保持恒定, 当气体射流喷出后, 燃烧器截面积扩展变大, 平均速度突然降低, 之后由于燃烧温度增加, 密度减小, 速度也随之增加, 当加入掺混水时, 由于质量的加入蒸汽速度略有上升, 直至液滴蒸发完全后速度保持稳定。压力经过计算在整个计算域内几乎保持一致, 因此可以认为燃烧器内的过程是一个等压过程。
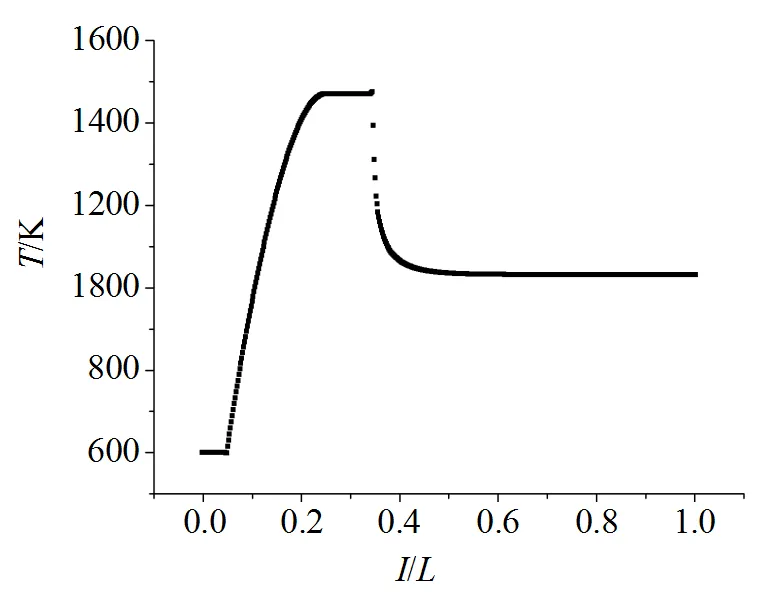
图3 含湿氢氧掺混燃烧燃气温度轴向分布

图4 含湿氢氧掺混燃烧燃气速度轴向分布
由液滴的粒径和温度变化图(图5和图6)可知, 初始阶段液滴粒径不变, 即无质量蒸发, 温度升高, 直至达到饱和温度后, 液滴开始蒸发, 之后温度保持饱和温度不变。液滴初始加入时轴向初速度为零, 随着液滴的运动, 其速度不断增加直至达到主流速度, 液滴速度变化过程如图7所示。液滴初始进入时由于速度较小, 轨迹变化较慢, 随着速度不断增加轨迹变化加快, 直至液滴达到主流速度时, 轨迹变化恒定, 液滴轨迹变化过程如图8所示。
不同粒径的液滴变化规律表明, 液滴粒径越小, 蒸发时间越短, 蒸发距离越小, 且随着粒径减小, 液滴惯性越小, 速度和温度变化更快。
2) 不同参数的含湿氢氧掺混燃烧
不同的氢氧入口含湿条件和冷却水掺混情况可以改变燃烧器内的各物理量分布, 图9为在燃料流量相同、掺混冷却水流量相同、氢氧入口含湿量不同时燃烧器内温度分布。由图可知, 燃料含水量越大, 其燃烧后温度越低, 加入掺混水时主流温度越低, 主流达到平衡温度所需距离越长, 液滴蒸发距离越长。
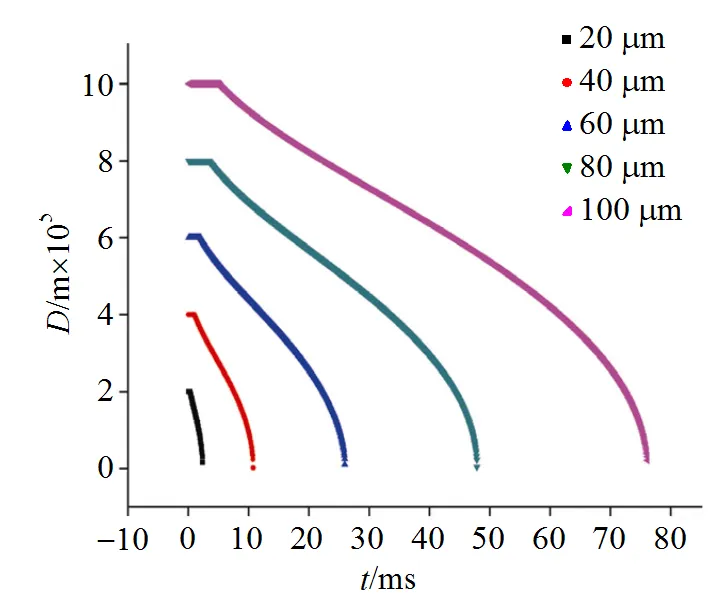
图5 不同尺寸液滴粒径随蒸发时间变化
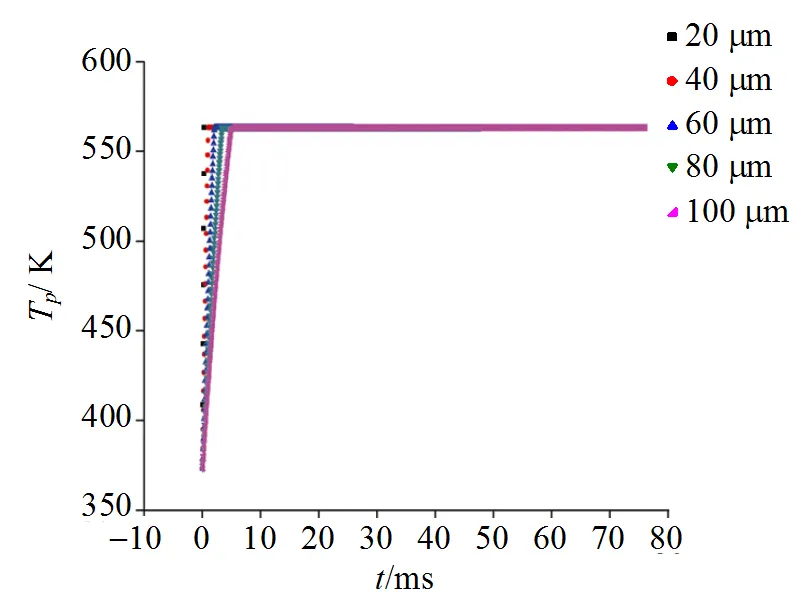
图6 不同尺寸液滴温度随蒸发时间变化

图7 不同尺寸液滴速度随蒸发时间变化

图8 不同尺寸液滴轨迹随蒸发时间变化

图9 含湿量不同时燃烧器温度分布
在距入口不同点处加入掺混水对燃烧器内分布也有很大影响, 氢氧入口含水量及掺混冷却水流量相同的情况下, 分别在距入口不同点处加入冷却水掺混, 得到燃烧器温度分布见图10。不同点处加入掺混水得到的温度分布不同, 在相同的主流温度加入掺混水时, 液滴蒸发距离相同。在燃烧区加入掺混水时, 温度由氢氧燃烧生成的热量和液滴蒸发吸收的热量共同控制, 液滴初始加入时蒸发吸热大于反应产热, 燃气温度下降, 随着液滴温度的升高, 质量逐渐减小, 液滴吸热不断减小直至小于反应产热, 燃气温度逐渐增加至平衡温度。由图10还可知, 在保证燃料含水量和掺混水量一定的情况下, 距入口不同点处掺入冷却水得到的最终温度相同, 符合能量守恒。
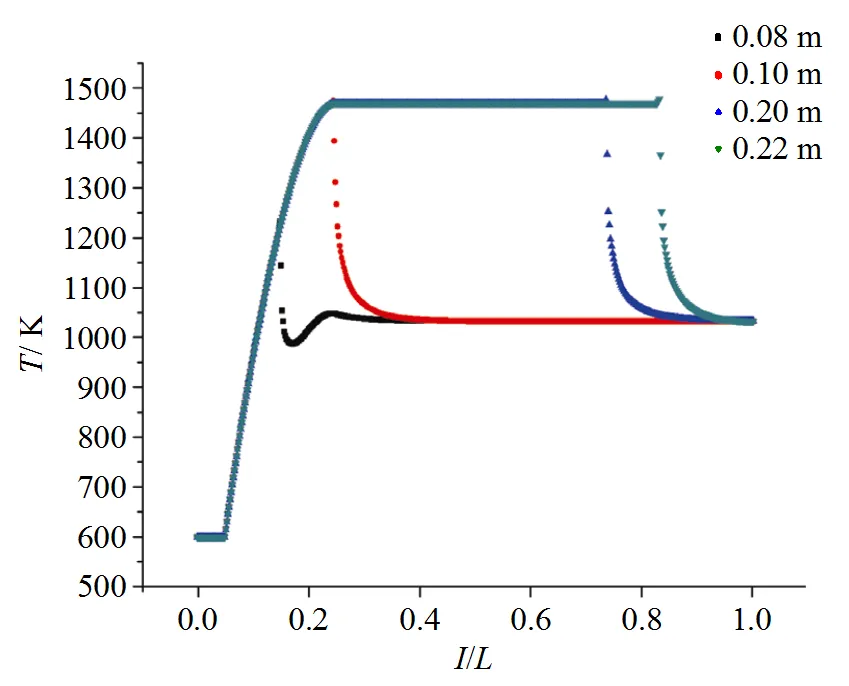
图10 不同点处加入掺混水时燃烧器温度分布
氢氧入口含水量相同, 在同一点加入不同流量的冷却水时燃烧器温度分布如图11所示。图中结果表明, 不同掺混水量最终的平衡温度不同, 掺混水量越大温度越低, 且掺混水量越大达到平衡所需的距离越长, 冷却水液滴蒸发所需距离越长。
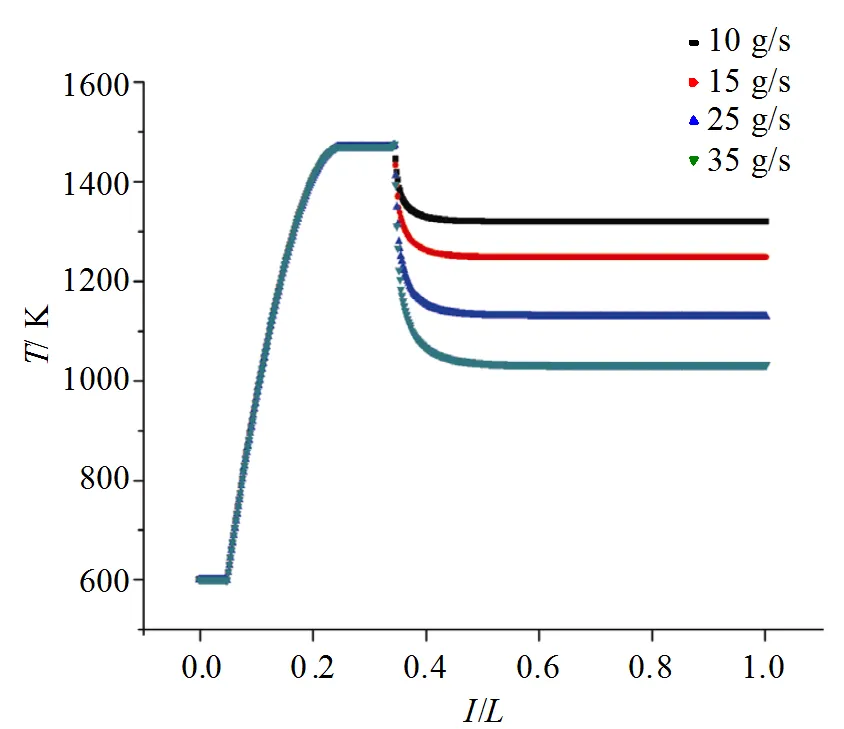
图11 加入不同量的掺混水时燃烧器温度分布
为了燃烧器的安全运行和得到符合汽轮机系统要求的蒸汽参数, 必须选择合适量的入口燃料湿度和掺混冷却水流量来控制输出蒸汽温度, 另外为了保证最终蒸汽中液滴完全蒸发, 还必须选择合理的距离点处加入掺混, 掺入点过于靠前, 在一定量的冷却水喷雾作用下氢氧可能无法点火或者无法稳定燃烧, 掺入点过于靠后, 会导致燃烧区温度过高或者出口蒸汽附带液滴。
5 结束语
本文通过分析氢氧加湿燃烧及液滴的运动变化过程, 基于文中建立的数学物理模型进行1D数值计算, 得到了燃烧器内的气相分布和液相的运动变化过程, 计算分析了不同的掺混冷却方案对含湿氢氧燃烧的影响, 经过与3D仿真结果对比, 液滴蒸发距离、蒸发时间、变化规律及气相变化结果基本相符, 表明文中所建理论和程序的合理性。
通常燃烧室中液滴蒸发包括燃料液滴的蒸发和燃气中冷却水液滴的蒸发[10], 这2种情况下蒸发环境为多元混合物且液滴表面和环境之间存在很大的浓度梯度, 液滴的蒸发主要由扩散作用所控制, 而本文所涉及的氢氧燃烧后水蒸气流中液滴的蒸发过程, 其蒸发环境为水蒸气流, 蒸发过程受控于液滴表面和环境之间的密度差(浓度差), 也就是由对流传质所决定, 本文建立的液滴模型对于认识水蒸气流中液滴的运动变化过程有重要的指导意义。
利用文中建立的1D计算程序可进行不同结构和工作参数下的燃烧器内氢氧加湿燃烧过程计算, 虽然1D数值模拟尚不能描述整个流场的细节, 但其计算量较2D和3D仿真大幅减少, 可为初步设计提供良好参考, 为后续研究打下基础。
[1] 温正, 石良辰, 任毅如. FLUENT流体计算应用教程[M]. 北京: 清华大学出版社, 2009.
[2] 周力行. 湍流两相流动与燃烧的数值模拟[M]. 北京: 清华大学出版社, 1991.
[3] Incropera F, DeWitt D P, Bergman T L, et al. Fundamentals of Heat and Mass Transfer(Six Edition)[M]. 葛新石, 叶宏,译. 北京: 化学工业出版社, 2007.
[4] 芮守祯, 邢玉明, 梁材, 等. 准一维超音速气液两相流数值模拟[J]. 热能动力工程, 2011. 26(4): 393-396, 489. Rui Shou-zhen, Xing Yu-ming, Liang Cai, et al. Numerical Simulation of a Quasi-one-dimensional Supersonic Gasliquid Two-phase Flow[J]. Journal of Engineering for Thermal Energy and Power, 2011, 26(4): 393-396, 489.
[5] 王福军. 计算流体力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
[6] 帕坦卡. 传热与流体流动的数值计算[M]. 北京: 科学出版社, 1984.
[7] 韩丹夫, 吴庆标. 数值计算方法[M]. 浙江: 浙江大学出版社,2006.
[8] 王应时, 范维澄, 周力行, 等. 燃烧过程数值计算[M]. 北京: 科学出版社, 1986.
[9] 赵坚行. 燃烧的数值模拟[M]. 北京: 科学出版社, 2002.
[10] 特纳斯(Turns, S, R). 燃烧学导论: 概念与应用[M]. 姚强, 李水清, 王宇, 译. 北京: 清华大学出版社, 2009.
One-dimensional Numerical Simulation of Humidified Hydrogen-oxygen Combustion
GAO Yu-ke, PENG Bo, HU Wei, HAN Xin-bo, LI Hong-wei, WAN Rong-hua
(The 705 Research Institute, China Shipbuilding Industrial Corporation, Xi′an 710075, China)
A new mathematical model of humidified hydrogen-oxygen combustion is built to describe combustion blending and cooling water evaporation process. One-dimensional simulation of different hydrogen-oxygen inlet and cooling water conditions are carried out to get the inlet parameters of influencing on humidified combustion by Euler-Lagrange method. The conclusion can provide a reference for analyzing humidified hydrogen-oxygen combustion process and designing combustion chamber.
humidified hydrogen-oxygen combustion; numerical simulation; combustor; atomization
TJ630.32
A
1673-1948(2013)02-0126-06
2012-08-30;
2012-09-12.
高育科(1986-), 男, 在读硕士, 研究方向为水下热动力技术.
(责任编辑: 陈 曦)
