用具有负介电常数的模拟光子晶体同轴系统获得负群速

姜荣，黄志洵

(中国传媒大学信息工程学院，北京 100024)

1 引言

Sommerfeld和Brillouin[1]在其经典的波速理论中指出在反常色散条件下，群速可能大于真空中光速，甚至为负。这引起了科学家们对反常色散媒质中的群速研究产生了极大的兴趣。1970年Garrett[2]等人的研究表明：当频率为f的电磁波通过非吸收但色散的媒质传播时，当媒质具有接近频率f的吸收线时就会出现反常色散的情况，此时群速可以大于光速，甚至为负，并且通过计算还表明对于吸收媒质来讲群速的概念同样具有意义。在1982年S.Chu and S.Wong[3]利用Garrett[2]提出的近吸收线的反常色散媒质首次测量到负群速。除此以外，科学家还利用增益线的方法实现负群速传播，其中尤其是2000年王力军[4]应用辅助增益线的方法实现反常色散首次在波形不失真的条件下观测到负群速，这使得观测到的群速更加具有意义。除了在这些有源的媒质实现电磁波的反常色散外，科学家们同样对无源媒质中电磁波的反常色散传播进行研究[5，6]，例如利用同轴晶体结构实现电磁波的反常色散传播[7-10]，其中文献[7，8]观测到超光速的群速，[9，10]观测到负的群速；利用波导系统实现类Fabry-Perot干涉仪达到电磁波的反常色散传播并观测负群速等[11]。

本文通过使用不同阻抗的同轴线周期相连形成模拟光子同轴晶体的同轴系统，由于阻抗不匹配，在某些频率形成阻带，在这些区域内出现反常色散的现象，通过计算得出反常色散区域处的超光速群速。然后假设其具有负折射率，计算电磁波的反常色散传播，获得了电磁波的负群速传播。

2 理论分析

使用图1所示不同阻抗的同轴电缆周期相连，得到模拟CPC的结构，来实现电磁波的反常色散性传播。为了计算色散需要确定折射率实部nr与相移φ的关系。由于在CPC中，不同阻抗的同轴电缆周期相连，在交界处不连续，存在入射波和反射波，因此电磁波的相位和振幅都发生变化。当电磁波通过总长度为L的CPC传播时相移可表示为：

(1)

其中k媒质中的波数，k0真空中的波数，c真空中的光速，因此CPC的折射率为：

(2)

为了计算相移需要计算CPC的反射系数R和传输系数T。

图1 同轴晶体结构。有两种不同阻抗的同轴电缆交替周期相连组成，共2m+1节。其中一种同轴电缆的阻抗为z1，长度为l1，波数为k1；另一种同轴电缆的阻抗为z2，长度为l2，波数为k2。

首先计算第2n节处的反射和透射系数。根据同轴线的电压电流公式以及连续的边界条件，可得：

a2nexp(-jφ2n)+Rznaznexp(jφ2n)

=T2na2nexp(-jφ2n)+R2n+1T2na2nexp(jφ2n)

(3)

(4)

整理后得第2n节的反射系数R2n和透射系数T2n分别为：

(5)

(6)

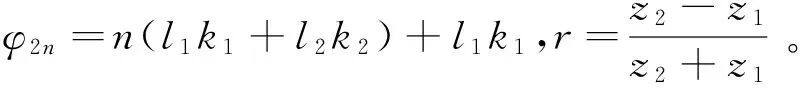
同理，可得第2n-1节的反射系数和透射系数

(7)

(8)

其中φ2n-1=n(l1k1+l2k2)。

令初始相移为零，得第2n-1节相移φ2n-1和第2n节的相移φ2n分别为：

(9)

(10)

通过迭代法可得总相移，最后算出有效折射率nr，再利用色散媒质中的群速公式进行计算

(11)

从而根据公式可得负群速传播的条件为：

(12)

3 CPC色散曲线和群速计算

首先，令图1所示的同轴晶体系统中z1=50，z2=75，l1=5m，lz=5m，m=7，电磁波在两种同轴线中的传播速度为0.66c，利用上述方法进行电脑计算，得到该系统的色散曲线和群速，见图2、图3，

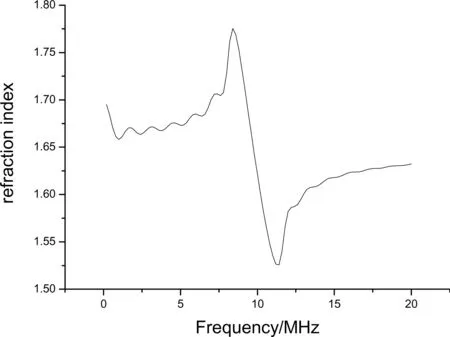
图2 CPC的色散曲线

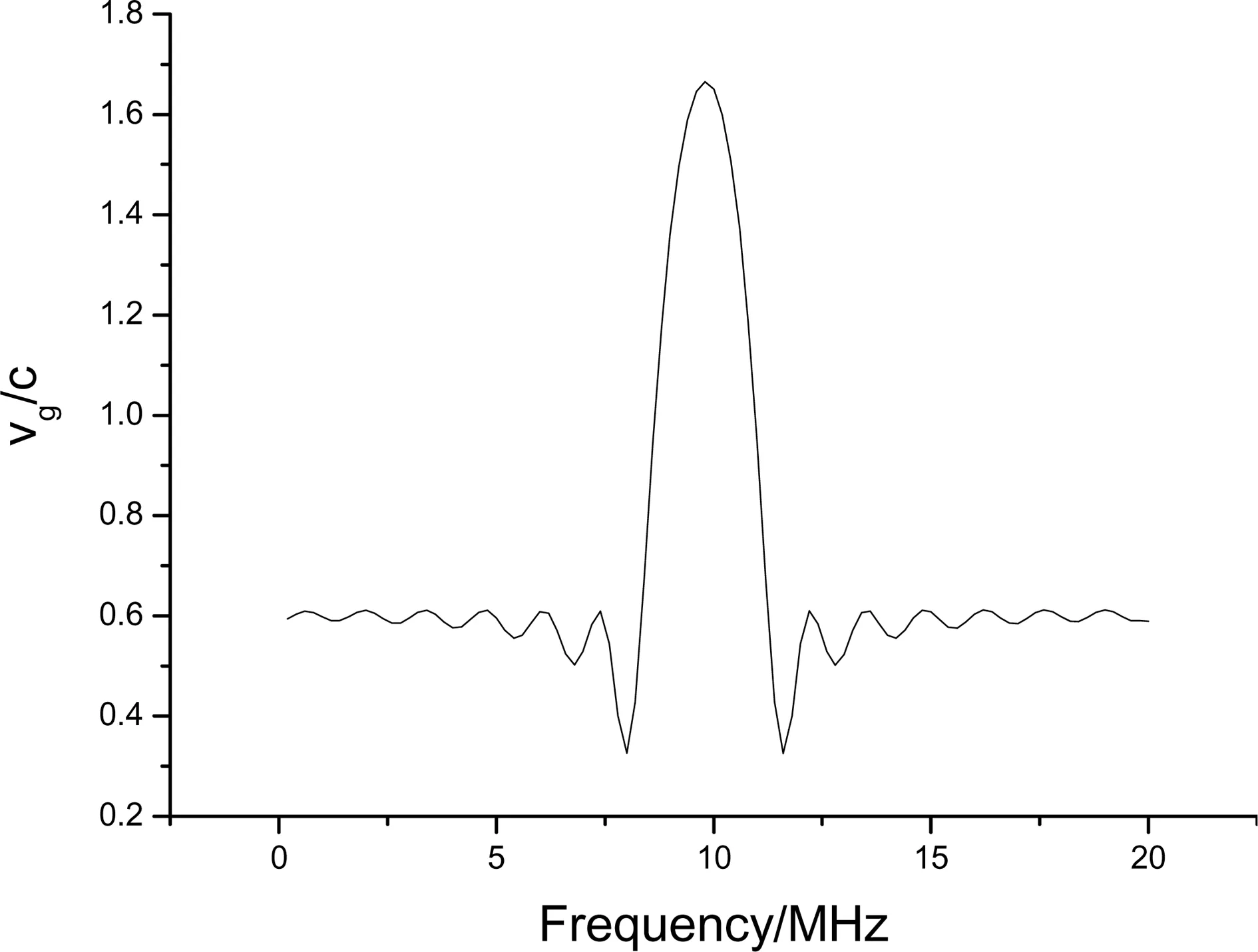
图3 CPC中电磁波的群速曲线

可见该CPC在8～12MHz出现反常色散，而在9～11MHz群速大于光速，最大群速可达 1.66c。

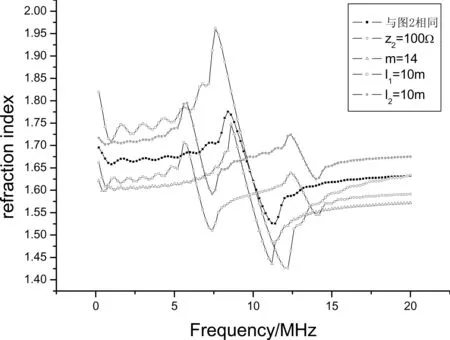
图4 不同参数对色散的影响

图5 不同参数对群速的影响

此后，我们对不同参数的CPC进行电脑计算，得到图4、图5。可以看出，改变系统参数会对色散曲线和群速都产生影响，当阻抗z2增大时反常色散区变宽，程度加深，群速变大(vg=2.66c)。当节数m增加时反常色散区基本不变，程度加深，群速变大，此时获得最大群速vg=3.25c，并且群速超光速的频带变宽。当增大每节长度l1或l2时，反常色散区改变，在两个区发生反常色散，但程度基本不变，群速大小的与图3相同(vg=1.66c)，只是出现两个超光速频带。通过公式(11)我们可以看出减小有效折射率nr并且大大的加深反常色散的程度可能会使群速变为负。根据上述研究，我们增大阻抗z2增加节数m，来加深反常色散，并使电磁波在同轴线中传播的速度达到c，即使如此群速也难变为负值。

4 获得负群速的一种方法

根据公式(11)若有效折射率nr为负，那么在该系统中群速就更容易变为负。假设电磁波在两种同轴线中的相速变为-0.66c，即折射率为nr=-1.5，其他参数不变，进行电脑计算结果见图6、图7，

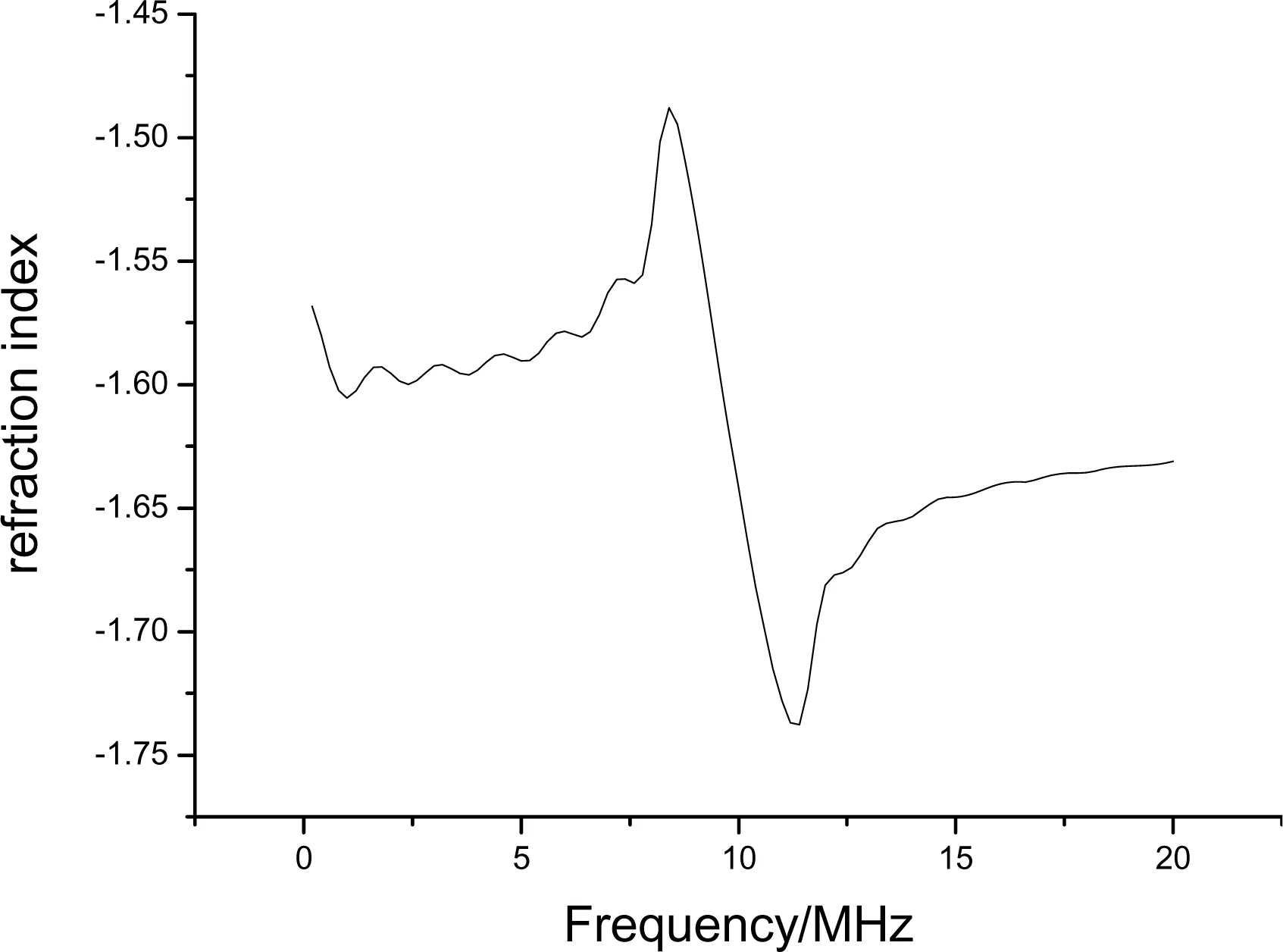
图6 折射率为-1.5的CPC的色散曲线

图7 折射率为-1.5的CPC中电磁波的群速曲线

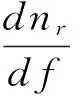
[1]Sommerfeld A，Brillouin L.Wave Propagation and Group Velocity[M].New York：Academic Press Inc，1960.

[2]Garrett C Q B，McCumber D E.Propagation of a Gaussian Light Pulse through an Anomalous Dispersion Medium[J].Phys Rev A，1970，1：305-313.

[3]Chu S，Wong S.Linear Pulse Propagation in an Absorbing Medium [J].Phy Rev Lett，1982，48：738-741.

[4]Wang L J，Kuzmich A，Dogarlu A.Gain-assisted Superluminal Light Propagation [J].Nature，2000，406：277-279.

[5]黄志洵.无源媒质中电磁波的异常传播[J].中国传媒大学学报(自然科学版)，2013，20：4-20。

[6]Huang Z X，Lu G Z，Guan J.Superluminal and Negative Group Velocity in the Electromagnetic Wave Propagation [J].Eng Sci，2003，1：35-39.

[7] Hache A，Poirier L.Long-range superluminal pulse propagation in a coaxial photonic crystal [J].Appl Phys Lett，2002，80：518-520.

[8]Lu G Z，Huang Z X，Guan J.Study on the Superluminal Group Velocity in a Coaxial Photonic Crystal [J].Eng Sci，2004，2：67-69.

[9]Munday J N，Robertson W M.Negative group velocity pulse tunneling through a coaxial photonic crystal [J].Appl Phys Lett，2002，81：2127-2129.

[10]周渭，李智奇.电领域群速超光速的特性实验[J].北京石油化工学院学报，2009，3：48-53.

[11]Carot A，Nimtz G.Giant Negative Group Time Delay by Microwave Adaptors [J].Euro Phys Lett，2012，98：64002 1-4.