基于修正的结构相似度为测度的三维脑图像配准
2013-05-06李京娜王国宏孙少燕
李京娜 王国宏 孙少燕 王 刚
基于修正的结构相似度为测度的三维脑图像配准
李京娜1,2王国宏1孙少燕3王 刚2
结构相似度通常用来评估图像质量。当空间位置发生改变时,图像间的结构相似度也会随之发生变化,近年已用作单模态图像配准测度。对其进行适当修改,提出一种新的基于像素灰度的配准测度——修正的结构相似度函数(MSSIM),并且应用于不同分辨率MR/CT及MR/PET三维临床脑图像(由Vanderbilt大学提供)配准中,算法首先做质心对齐,然后利用Powell算法“由粗到精”对下采样图像配准,再由8点法评估配准质量。结果显示,此测度函数具有良好的配准性能,能够完全自动地达到亚像素级配准精度,鲁棒性较高,但运算速度也较慢。
脑图像;图像处理,计算机辅助;结构相似度函数;图像配准
随着现代医学仪器的发展,计算机辅助图像处理理论和技术已经广泛应用于临床医学影像设备。图像配准是其中一个重要环节,其方法一般分为基于像素灰度(intensity-based)的方法和基于图像特征(featurebased)的方法[1]。算法流程的一个关键环节是测度函数的选取[2],在医学图像配准领域常用互信息MI(mutual information)[3]及归一化互信息NMI(normalization mutual information)[4]为测度函数[5-7],通过改进,配准精度一般能够达到亚像素级。由Wang等[8]基于人类视觉系统(human visual system, HVS)特点提出的结构相似度函数(structural similarity, SSIM),通常用来评估图像质量[9,10],而Sánchez-Ferrero等[11]将SSIM用来评估单模态图像的配准质量;Wang等[12]在配准数字减影血管造影(DSA)实验中,首先用Harris角点检测子提取兴趣点,然后在空间坐标位置不超过一定范围的约束下,分别以SSIM和MI为相似性测度对两个图像的兴趣点进行匹配,最终找到一一对应关系,虽然此实验的结果是SSIM测度的配准性能优于MI测度,但只是针对DSA影像单模态情况下的兴趣点匹配,未研究多模态情况下的图像配准,如DSA与CT、MRI等影像之间的配准;Amintoosi等[13,14]把结构相似度作为灰度方差和(SSD)测度的权重,改进了Lucas-Kanade(LK)算法对单模态图像的配准性能,但未将SSIM直接作为配准测度;Ben Sassi等[15]直接以SSIM为配准测度通过优化算法得到MR图像的配准参数,但仍然是对单模态图像配准,未涉及多模态图像配准。本文在结构相似度SSIM的基础上,通过适当的修改,采用一种新的配准测度——修正的结构相似度函数(modified structural similarity, MSSIM)[16],通过分析,这种测度函数的匹配曲线为比较光滑的上凸函数,全局最大值的收敛范围较宽,具有良好的配准性能,利用Powell优化算法、简单的双线性插值技术对不同成像模式的三维临床脑图像进行6个自由度仿射变换(即刚体变换),然后采用8点法[17]对配准精度进行评估,取得了比较满意的结果,同时由于不同设备的分辨率有所差别,临床图像在配准前需要进行预处理,本文在配准方法中作一详细论述。
1 配准原理
结构相似度函数综合了图像间亮度、对比度及结构3个方面信息的比较,计算采用滑动窗口方法,先求出每一对子窗的结构相似度值,然后对所有结果求均值。每一对子窗的结构相似度大小定义为:
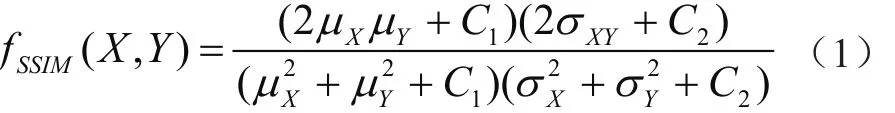
其中X、Y代表原始(或参考)图像的子图像与待评估(或浮动)图像的子图像(如第j对子图像表示为Xj、Yj),C1、C2为小的正常数,以防止分母为0而出现不稳定;μX、μY、σX、σY、σXY分别表示X、Y的亮度均值、标准差与协方差,其中协方差σXY定义为:
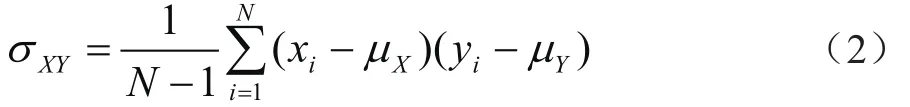
N为子图像的像素个数。对于完全相同的两幅单模态图像,当空间位置完全对齐时,每一对子图像间σXY=σX2=σY2,则fSSIM(X,Y)=1,若两图像空间位置发生偏离(包括平移、旋转、缩放等空间变换),随着偏离度的增大,fSSIM随之减小,变化曲线(即匹配曲线)为上凸函数[8];但是对于多模态图像,由于图像间内容差异较大,对齐时fSSIM一般不等于1,尤其是当成像亮度相反的两幅图像对齐时,子图像间σXY<0,导致fSSIM不再是最大值,而且fSSIM匹配曲线不再是上凸函数,为此对公式(2)进行修改,用|σXY|代替σXY,结果发现修改后的结构相似度的配准曲线,不论是单模态还是多模态图像,均为良好的上凸函数,其中旋转及缩放曲线比较光滑,平移曲线有不明显的局部极值,图像匹配时对应全局最大值,并且全局最大值附近比较光滑,收敛范围比较宽。修正的结构相似度定义为:
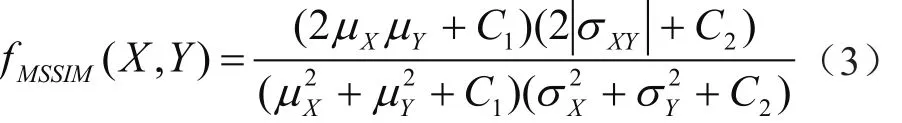
0≤fMSSIM≤1,其中C1=(K1L)2、C2=(K2L)2,K1<<1、K2<<1,L是像素的动态范围(若是8位灰度图像则L=225,取K1=0.01,K2=0.03)。在进行计算时采用滑动窗口方法,首先按照公式(3)计算各个窗口内(子图像)的fMSSIM值,然后对所有子图像进行累加平均:
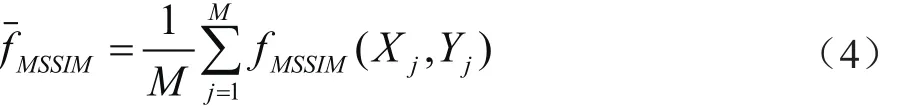
其中M为子图像个数,Xj和Yj分别代表参考图像和浮动图像的第j个子图像。fMSSIM为MSSIM的度量值。
2 测度曲线分析
实验运行于ThinkPad T410i [Intel(R) Core(TM) i5 CPU, M 430@ 2.27 GHZ 2.27 GHZ, RAM 3.00 GB]、Matlab 7环境。同一例患者不同模态图像MR和CT取自Harward whole brain atlas其中的Neoplastic Disease(brain tumor),格式为GIF,大小为256×256(map 128×3)(http://www.med.harvard.edu/AANLIB/cases/case28/ mr2/010.html),图像初始状态严格对齐,见图1。分别以MSSIM、SSIM以及NMI等为配准测度,研究多模态图像配准特性,采用双线性插值(bilinear),平移的动态范围为[-50,50],以0.2个像素为变化步长;旋转的动态范围为[-50,50],以0.2°为变化步长;缩放的动态范围为[0.1,2.1],以0.1为变化步长,见图2~4。

图1 多模态脑图像MR-T2/CT,大小256×256。
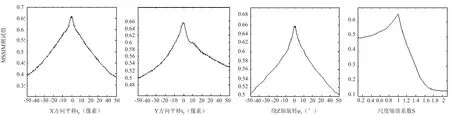
图2 MSSIM测度多模态图像MR-T2/CT匹配曲线
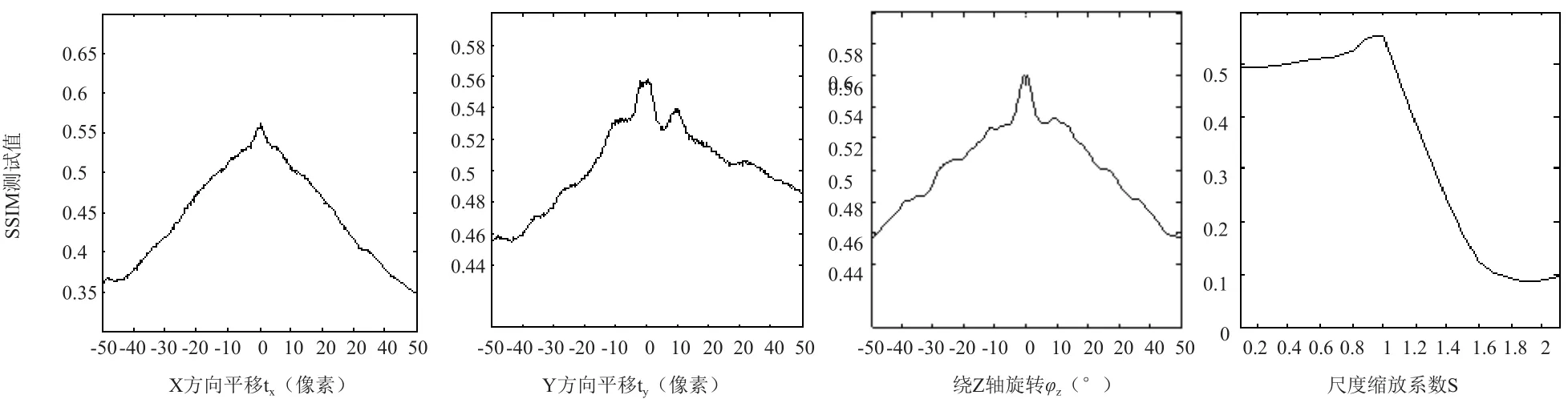
图3 SSIM测度多模态图像MR-T2/CT匹配曲线
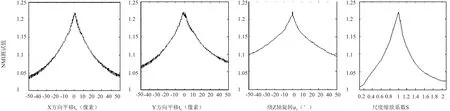
图4 NMI测度多模态图像MR-T2/CT匹配曲线
图2 和图4表明,MSSIM测度与经典的NMI测度配准特性非常相似,多模态图像匹配曲线为良好的上凸函数,平移曲线中出现的锯齿状局部极值(又称为interpolation-induced artifacts)是由线性插值引起,但这种局部极值通过插值改进可以有效抑制。图3表明,未经过修正的SSIM测度,其多模态匹配曲线已经不是凸函数或凹函数,并且出现了大量的强局部极值,甚至会使图像对齐位置(即相似度最大值)出现凹陷,使优化过程陷入局部极值导致误匹配。
3 基于MSSIM的三维脑图像配准方法
本文用到的所有临床数据均来源于美国田纳西洲Vanderbilt大学的“回顾性图像配准算法评估”项目(Retrospective Image Registration Evaluation, RIRE, http://www.insight-journal.org/rire/index.php),其中患者影像文件编号为training_001。由于3D图像数据量较大(如training_001的MR图像分辨率为256×256×26体素,CT图像分辨率为512×512×29体素,正电子发射断层PET图像为128×128×15体素),为了提高算法的速度和精度,采用“先粗后精”配准策略,具体步骤如下。
3.1 按照网站提供的信息重新读取图像 从第1层的第1行的第1列开始逐列→逐行→逐层读取,图像信息转变为3D数组R0(voxels)和F0(voxels)。
3.2 质心对齐 采用质心主轴法[17,18]得到待配准两个图像的质心坐标(单位为体素voxels),然后根据图像各自的体素大小,把质心坐标的单位由体素转变为毫米,同时把以体素为单位的图像转变成以毫米为单位的图像R0(mm)和F0(mm),之后把浮动图像F0(mm)的质心平移到参考图像R0(mm)质心位置。
3.3 粗配准 以图像R0(mm)和F0(mm)的质心为中心沿x、y、z正、负方向每隔4 mm采样一次(即采样率为1/4),设定采样图像尺寸为61×61×61(单位为体素,每个体素大小为4×4×4 mm3),得到采样图像R1(voxels)和F1(voxels),然后采用Brent一维搜索算法及改进的Powell多维方向优化算法[19]完成粗配准,其中优化过程的搜索顺序设定为(tx, ty, φx, φy, φz,tz)[17],配准参数向量为[tx, ty, tz, φx, φy, φz],优化参数起始向量为[0,0,0,0,0,0],迭代精度0.0001,一维搜索的起始动态范围为[-10,10],然后以“ceil(±10/迭代次数)”逐步缩小动态范围,步长为0.5,采用双线性(bilinear)插值法,获得的参数尤其是平移参数需要根据采样率做适当处理,作为精配准时优化参数的起始向量。
3.4 精配准 以图像R0(mm)和F0(mm)质心为中心沿x、y、z正、负方向每隔2 mm采样一次(即采样率为1/2),设定采样图像尺寸为121×121×81(单位为体素,每个体素大小为2×2×2 mm3),得到采样图像R2(voxels)和F2(voxels),然后采用与粗配准相似的方法进行精配准,为了节省运算时间同时提高配准精度,一维搜索的起始动态范围减为[-6,6],步长为0.1,由于是1/2采样,配准得到的平移参数需要乘以2才能作为最终精配准的平移参数。
由于空间变换的次序会影响变换的结果[17],所以对采样图像配准时,首先设定笛卡尔(Cartesian)坐标系正方向:x方向从左向右、y方向从后向前、z方向从下向上(满足右手定则),顺时针旋转为正方向;然后设定配准过程的空间变换次序为:x方向平移tx、y方向平移ty、z方向平移tz→将笛卡尔坐标系的原点由采样图像左后下角平移到采样图像中心→y_z剖面绕x轴旋转φx、x_y剖面绕y轴旋转φy、x_y剖面绕z轴旋转φz→将笛卡尔坐标系的原点由采样图像中心移回到采样图像左后下角。如果图像大小为m×n×r,则空间变换矩阵为:

其中
4 结果与分析
图5、6为三维脑图像的配准结果。图5A、B为MR-T2-rectified和CT第40断层的1/2采样图像,分别为参考图像和浮动图像,图5C为配准后(0.5×参考图像+0.5×配准后浮动图像)的融合图像;图6A、B为MR-T1和PET第40断层的1/2采样图像,图6C为配准后的融合图像。
为了定量评估配准精度,首先重组质心坐标和精配准参数,得到最终的配准参数向量,然后采用8点法评估配准精度,其中初始失配误差(initial RMSE)和配准后误差(registration RMSE)分别由给定的8个点配准前后物理坐标的均方根误差(root-mean-square error, RMSE)计算配准前initial RMSE值[公式(6)]和配准后registration RMSE值[公式(7)]。
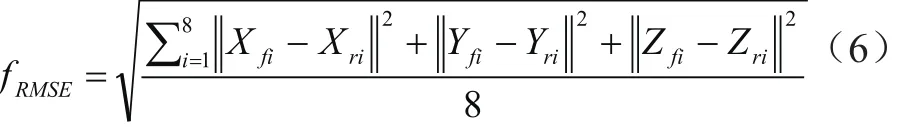
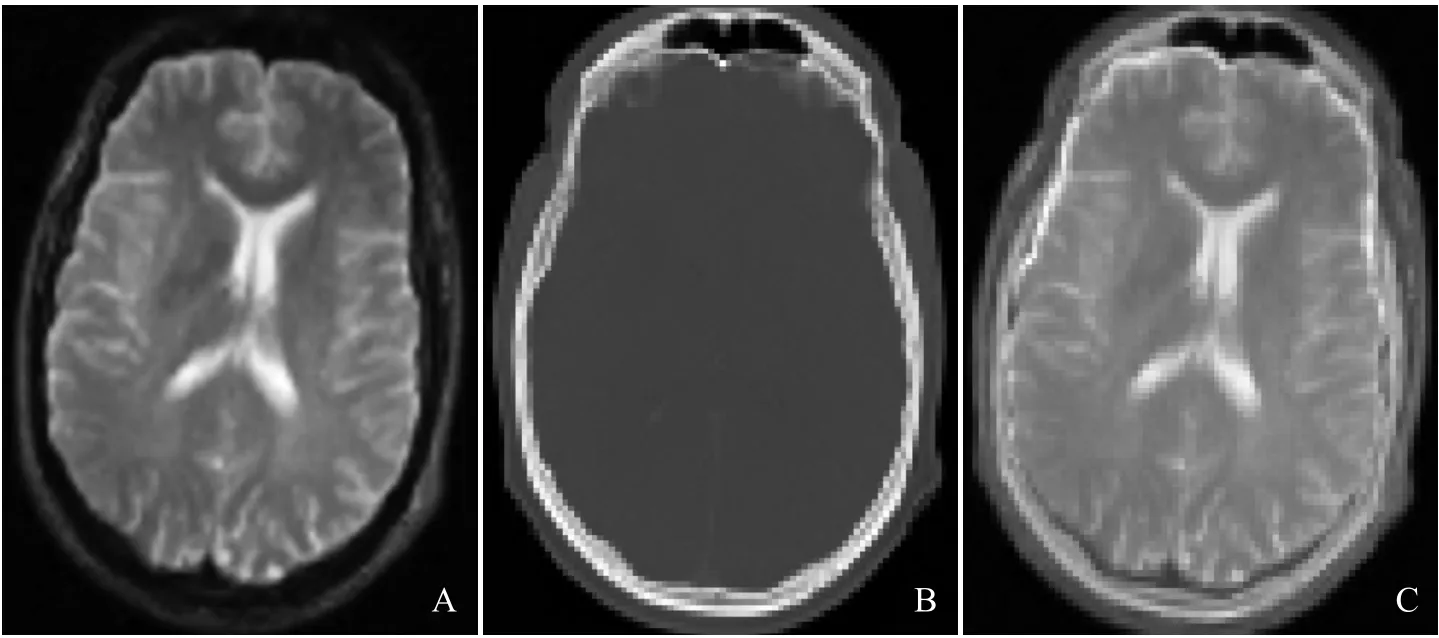
图5 MR-T2-rectified和CT的1/2采样图像第40断层配准结果。
图6 MR-T1和PET的1/2采样图像第40断层配准结果。

变换矩阵T由公式(5)求得,其中的变换参数[tx,ty, tz, φx, φy, φz]由Powell优化得到;Xri、Yri和Zri表示参考图像上给定的8个点的物理坐标;Xfi、Yfi和Zfi表示配准前浮动图像上给定的8个点的物理坐标;TXfi、 TYfi以及TZfi表示配准后浮动图像对应的8个点的物理坐标;体素大小(voxel size)定义为单个体素的对角距,从两个图像中选取较大的体素与配准后误差比较[17],结果见表1。
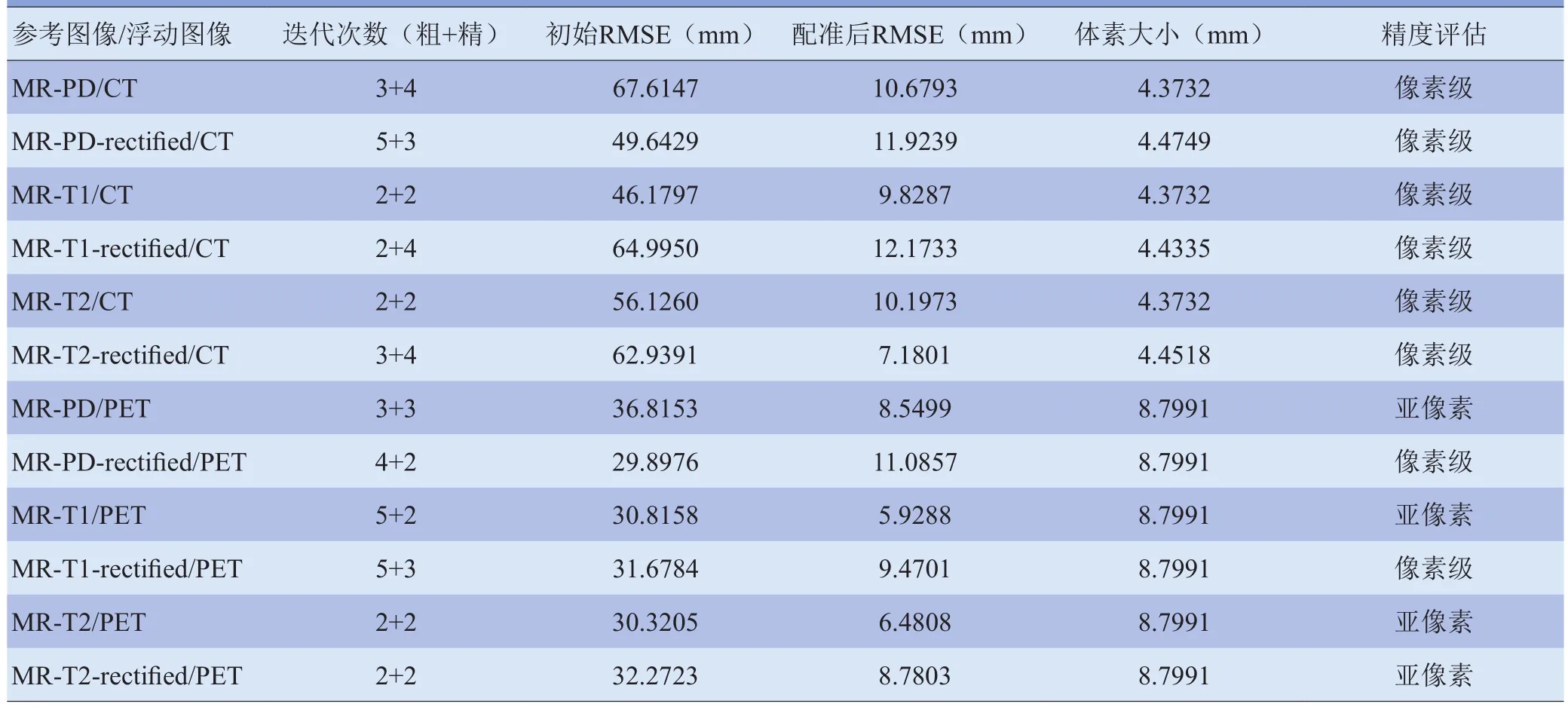
表1 临床脑图像MR/CT及MR/PET的配准结果
表1中迭代次数(number of iteration)指粗、精配准迭代次数之和;精度评估(accuracy assessment)是把配准后RMSE与体素大小比较得到的,本文假设,如果配准后RMSE小于1个体素大小,则为亚像素级配准(sub-voxel-level);如果小于3个体素但大于1个体素,则为像素级配准(voxel-level);大于3个体素则意味着配准失败。配准结果表明,MSSIM测度对图像的分辨率不敏感,MR-T2/CT和MR-T2/PET的配准结果接近;但由于PET的分辨率较低,体素较大,因而评估结果大部分为亚像素级精度;由于图像内容、分辨率差异将导致局部极值增多,尤其是插值产生锯齿状伪极值(artifacts)造成匹配曲线全局最大值产生峰移(peak-shift)[5],匹配曲线的光滑度、尖锐度随之变差,因而降低了配准精度。图7A、B分别为MR-T2/CT和MR-T2/PET的1/2采样图像第40断层MSSIM测度平移曲线,均采用双线性插值法,横坐标步长为0.2,纵坐标为MSSIM度量。平移曲线的artifacts比较明显,如果采用样条插值(spline),曲线将变得平滑,但同时使计算量剧增;artifacts导致峰移,即使采用样条插值也不能避免。由于MR-T2与PET图像像素分辨率差异较大,其中PET分辨率较低,导致其匹配曲线局部极值较多,由于算法首先采用质心对齐和1/4采样粗配准,保证了精配准的有效收敛。
由于计算机硬件的限制,最终的配准参数是质心坐标差和采样图像精配准参数组合得到的,采样率也会影响配准精度,但MR与PET图像的配准仍然能够达到亚像素级精度,说明本文提出的新的配准测度函数MSSIM以及相应的配准算法对临床3D图像刚体变换具有一定的应用价值,但由于运算速度较慢,不具有实时性。
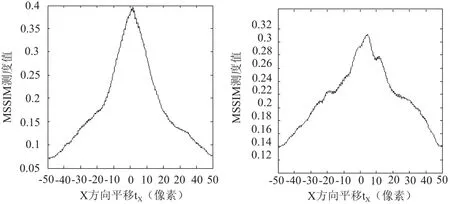
图7 MR-T2/CT/PET的1/2采样图像第40断层MSSIM测度平移曲线。
5 结束语
本文提出的新的配准测度——修正的结构相似度函数(MSSIM),配准特性与经典的NMI测度接近,对单模态和多模态图像都具有比较好的配准性能,在不同分辨率的3D临床脑图像刚体变换配准中,图像经过适当的采样处理,并且采用“先粗后精”的配准策略,能够达到亚像素级配准精度,对图像的分辨率不敏感,鲁棒性较高,但由于数据量较大,配准速度仍然较慢,不具有实时性;而插值引起的伪极值artifacts会降低配准精度及鲁棒性,需要对MSSIM函数本身以及配准算法进行不断改进。
[1] Zitová B, Flusser J. Image registration methods: a survey. Image Vis Comput, 2003, 21(11): 977-1000.
[2] Shams R, Sadeghi P, Kennedy RA, et al. A survey of medical image registration on multicore and the GPU. IEEE Signal Process Mag, 2010, 27(2): 50-60.
[3] Maes F, Collignon A, Vandermeulen D, et al. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging, 1997, 16(2): 187-198.
[4] Studholme C, Hill DG, Hawkes DJ. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognit, 1999, 32(1): 71-86.
[5] Chen HM, Varshney PK. Mutual information-based CT-MR brain image registration using generalized partial volume joint histogram estimation. IEEE Trans Med Imaging, 2003, 22(9): 1111-1119.
[6] 余慧婷, 张杰, 潘萌. 噪声对三维图像归一化互信息配准的影响. 中国医学影像学杂志, 2011, 19(11): 844-849.
[7] 王丽, 孙丰荣, 王奕琨, 等. 基于互信息的颅脑MR影像序列的三维配准. 计算机工程与应用, 2011, 47(31): 160-163.
[8] Wang Z, Bovik AC, Sheikh HR, et al. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process, 2004, 13(4): 600-612.
[9] 韩国强, 李永祯, 王雪松, 等. 基于修正SSIM的SAR干扰效果评估方法. 电子与信息学报, 2011, 33(3): 711-716.
[10] 蒋刚毅, 黄大江, 王旭, 等. 图像质量评价方法研究进展.电子与信息学报, 2010, 32(1): 219-226.
[11] Sánchez-Ferrero GV, Vega AT, Grande LC, et al. Strain rate tensor estimation in cine cardiac MRI based on elastic image registration//Tensors in image processing and computer vision. London: Springer, 2009: 355-379.
[12] Wang J, Zhang JQ. An iterative refinement DSA image registration algorithm using structural image quality measure// Intelligent information hiding and multimedia signal processing, 2009. IIH-MSP'09. Fifth International Conference. IEEE, 2009: 973-976.
[13] Amintoosi M, Fathy M, Mozayani N. Precise image registration with structural similarity error measurement applied to superresolution. EURASIP Journal on Advances in Signal Processing, 2009: 305479.
[14] Amintoosi MM, Fathy M, Mozayani N. Video enhancement through image registration based on structural similarity. Imaging Science Journal, 2011, 59(4): 238-250.
[15] Ben Sassi O, Delleji T, Taleb-Ahmed A, et al. MR image monomodal registration using structure similarity index//Image processing theory, tools and applications, 2008. IPTA 2008. First Workshops. IEEE, 2008: 1-5.
[16] 李京娜, 王国宏, 孙少燕, 等. 基于修改后的结构相似度的三维图像配准. 光电工程, 2012, 39(12): 70-76.
[17] 罗述谦, 周果宏. 医学图像处理与分析. 北京: 科学出版社, 2003: 140-201.
[18] 王玉, 王明泉, 李志刚, 等. 基于互信息的医学图像快速准确配准策略. 中国组织工程研究与临床康复, 2008, 12(9): 1669-1672.
[19] 唐焕文, 秦学志. 实用最优化方法. 第3版. 大连: 大连理工大学出版社, 2004: 147-149.
(责任编辑 张春辉)
Three-dimensional Image Registration Based on Modified Structural Similarity
LI Jingna WANG Guohong SUN Shaoyan WANG Gang
Structural similarity is often used to assess image quality. The function that structural similarity between images changes along with spatial location has been employed in one-dimensional image registration in recent years. We modified it and put forward a new registration metric based on voxel gray-modified structural similarity (MSSIM), applying to three-dimensional brain image registration of MR/CT and MR/PET with different resolution (provided by the Vanderbilt University). It started from centroid alignment, and then sample image registration was performed according to the Powell Algorithm, followed by quality assessment by eight-point algorithm. It turned out that the registration metric performed well and could reach the accuracy of sub-pixel registration fully and automatically. The robustness was high but the operation was rather slow.
Brain image; Image processing, computer-assisted; Structural similarity; Image registration
10.3969/j.issn.1005-5185.2013.08.017
1. 海军航空工程学院电子信息工程系 山东烟台 264001
2. 鲁东大学信息与电气工程学院 山东烟台264025
3. 鲁东大学数学与信息学院 山东烟台264025
李京娜
Department of Electronic and Information Engineering, Naval Aeronautical Engineering Institute, Yantai 264001, China
Address Correspondence to: LI Jingna
E-mail: ljn6502@126.com
鲁东大学横向基金项目(2010HX007)。
R445
2013-03-19
修回日期:2013-07-06
中国医学影像学杂志
2013年 第21卷 第8期:618-623
Chinese Journal of Medical Imaging
2013 Volume 21(8): 618-623
