浅谈如何在初中几何教学中培养学生的思维品质
2013-04-29郭昕
郭昕
初中数学几何教材作为数学形象知识的载体,对于提高初中学生逻辑思维能力,培养学生想象力发挥着重要作用,能够真正促进学生几何思维品质的提高。几何教学作为初中数学教学中的重要组成部分,是学生初次接触和认识逻辑体系结构的学科。几何教学对于实现初中数学教学目标有着良好的促进作用。
一、初中几何教学中学生思维能力的培养目标
据调查研究统计,几何教学的作用主要体现在学生对图形结构的认识、空间想象能力和逻辑思维的训练等。几何教学严格的逻辑推理有助于培养学生掌握数学思想,形成缜密的数学思维,锻炼学生发现问题、分析问题和解决问题的实践能力。
初中数学几何教学能够使学生获得发展和提高数学知识,包括数学思维逻辑、数学思想方法、数学活动规律等必要技能。使学生学会如何运用几何思维去观察事物、分析真相,由此来解决日常生活中容易出现的数学问题,增强学生运用数学知识、发挥个人想象力的意识。使学生能够真正了解几何知识的内在价值,提高对数学知识的理解能力和思考能力。培养学生一定的开拓创新精神和能力,使学生的知识技能能够得到进一步提升。
二、初中几何教学中学生思维能力的培养策略
1.学生思维严密性的培养
思维严密性指的是大脑思考符合正常的逻辑思维,并且保证思维的准确缜密。初中数学的几何教学在培养学生思维的严密性方面发挥着关键作用。教师可以从以下几个方面加强对学生思维严密性的培养:一是几何概念的讲解准确清晰;二是明确逻辑结构关系;三是对几何概念和解题方法正确分类;四是在布置学生完成任务时,要求学生的几何证明保证有据可依、因果明确,注意解题过程的逻辑性和条理性,防止解题过程中出现证明条件不符、定理不准确的现象;五是逐渐向学生渗透公理化思想。
2.学生思维深刻性的培养
思维深刻性指的是大脑思维活动中逻辑抽象的程度,思维深刻性表现为学生善于使用几何抽象概念,推理过程缜密,理解透彻深刻,以此解决难度较大的数学几何问题。如果学生的思维深刻,便能够透过事物的表面现象抓住问题的本质,掌握问题的规律,通过总结归纳某些特殊现象而得到问题的规律。当完成几何问题的解题后,能够较好地掌握题型规律和解题方法,将自己获得的方法应用于其他问题中。
3.学生思维广阔性的培养
思维的广阔性指的是大脑思路宽阔,能够从多方面、多层次、多角度对问题进行探索。如果学生的思维广阔则能够整体把握几何问题,不但能够掌握几何问题的基本特征,还能够抓住问题的关键因素,拓展思路,积极思考。由此,在初中数学几何教学中,教师可以积极培养学生一题多解的能力,以此来培养学生思维的广阔性。
4.学生思维敏捷性的培养
思维敏捷性指的是大脑思维活动中对事物的反应速度。思维敏捷性表现为学生在思考几何问题时,是否能够立刻做出敏锐反应。在初中数学几何教学中,教师可以从以下几个方面培养学生的思维敏捷性:一是积极培养学生的猜想能力,加强问题猜想联系;二是对于固定的几何题型要多加练习,帮助学生形成良好的思维策略;三是对部分几何问题采用变式训练的方法,促进学生对几何知识点的运用;四是培养学生从几何问题中总结规律、掌握方法。
三、初中几何教学中学生思维深刻性培养的教学案例
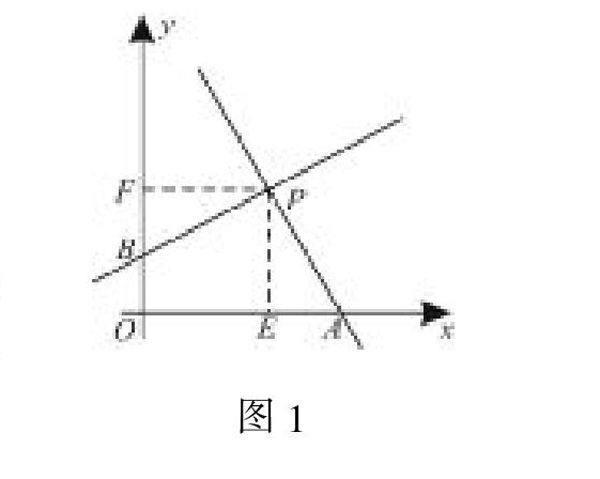
例1 如图1所示,在坐标系中,点P(a,a)处于第一象限内,过点P作两条直线分别于x轴和y轴相交于A、B两点,记作PA、PB.直线PA和PB分别绕P点进行转动,让时刻保持它们相互垂直。
问题:四边形PAOB的面积是否会随着直线的运动发生变化?请给出证明理由。
解:如图1所示,分别作两条辅助线, PE垂直于x轴,PF垂直于y轴,由此可知,四边形PAOB的面积与PEOF的面积完全相等,因此,四边形PAOB的面积等于a2,面积不会随着直线运动发生变化。
如果学生能够对几何例题1的解题思路和方法有较为深刻的理解,总结出该类几何题型解题思路和规律,便能够很好地将解题方法迁移应用于其他数学问题中(例2),由此达到举一反三、触类旁通的目的,也是培养学生思维深刻性的必要条件。
例2 在正方形ABCD中,点O是正方形的中心,将一个圆心角为直角、半径长度足够的扇形铁板置于正方形ABCD之上,与点O相交,将扇形铁板以点O为中心缓慢旋转。证明:正方形ABCD被扇形铁板覆盖的面积恒定不变。
综上所述,新课程改革背景下,对于初中数学几何教学内容做出了新的要求,教师和学生都需要不断适应教学改革的变化,积极探索更为有效的教学方法,完成几何教学工作。在几何问题的推理过程中,加强培养学生的逻辑思维能力和想象力,使学生逐渐形成理性思考几何问题的习惯。
