教学“判定三角形全等”的一条主线
2013-04-29黄发德
黄发德
摘 要:“判定三角形全等”是初中数学教学中的难点,教学实际中要抓住教材重点,引导学生进行学习突破。
关键词:判定三角形全等;主线;数学教学
三角形全等的判定,方式多,条件繁杂,学生容易混淆,不易掌握。如果有一条主线将其串联起来,有助于学生对判定方法的理解和掌握。
一、边边边
(探究一)将三根木条钉成一个三角形木架,这个三角形的形状大小就确定了。用三组分别相等的小棒,摆两个三角形,观察得到“三边分别相等的两个三角形全等”这一基本事实。
(探究二)用尺规作图,画两个三边分别相等的三角形,借助太阳光,观察这两个三角形是否全重合,从而验证“三边分别相等的两个三角形全等”。
二、角角角(假命题)
观察三角板上的两个三角形,它们的三角分别相等,可这两个三角形并不全等。通过这认识到一个三角形,确定了它的三个内角,只确定了这个三角形的形状,而不能确定它的大小。如果想要完全确定一个三角形,还必须确定某一条边长。
三、两角一边(角边角,角角边)
(推理)根据三角形内角和定理,如果两个三角形的两角分别相等,那么这两个三角形的第三组角也一定相等。两个角分别相等如果再有一边相等,不论是它们的夹边还是一个角的对边,这两个三角形全等。
即:(1)两角和它们的夹边分别相等的两个三角形全等。
(2)两角和其中一个角的对边分别相等的两个三角形全等。
四、两边一角
1.两边一夹角
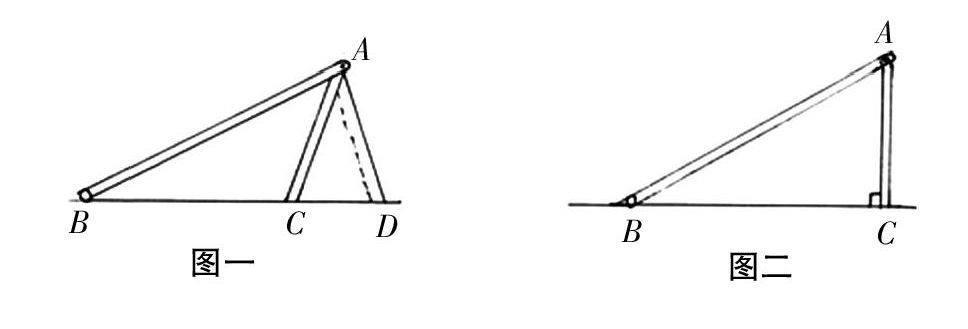
观察到一个三角形两边和一边的对角确定,因为有一边可能在左、右两个位置上任意摆动,所以这个三角形的形状往往不能确定。由实验得到:“两边和一边的对角相等的两个三角形全等”又是一个假命题。
(探究二)上述实验中,正是因为有一边左、右摆动,使得三角形的形状不能确定。如果让这条边直立不动(如图二)也就消除这条边左、右摆动的情况,确保三角形形状不变,于是就成为一个直角三角形。由实验得到“在两个直角三角形中,如果两边(斜边和直角边)和其中的一边(斜边)的对角(直角)分别相等,那么这两个三角形全等”。于是“两边和一边对角相等的两个三角形全等”这一假命题,在直角三角形这一特殊环境中却变成了真命题,“斜边、直角边分别相等的两个直角三角形全等”。
我们在探究“判定三角形全等至少需要的三个边角条件”的教学中,按三边、三角、边角结合的主线进行逐一探究,得到“边边边”“角角边”“角边角”“边角边”和“斜边、直角边”等几个判定方法,并且正确认识“角角角”“边边角”两个假命题,从而全面系统地掌握了三角形全等的判定方法。
在教学过程中,按知识的某一逻辑顺序,让知识形成一定结构体系,串成线,结成片,相互关联地、动态地、系统地被学生所掌握,有助于教学质量的提高。
(作者单位 青海省格尔木市八一中学)
