浅谈四边形的教学

王兴文

摘 要：为了使数学课堂教学充满生机与活力并激发学生的创新意识和探索精神，以四边形的教学实践与认识为例，提出相应对策：改变教学形式，重视数学活动；创设问题情景，激发学生求知欲；运用现代教育技术手段和直观教具，提高学习效果；鼓励合作学习，培养创新能力；教给学习方法，提高学习效率。

关键词：教学形式；创设情境；合作学习；学习方法；多媒体技术

长期以来，数学教学在沉闷、缺乏生气中进行。学生没有学习热情，没有积极性，怕数学，更不用说激发创意和不断探索的精神了。很多数学老师都在苦苦探索和寻求解决这个问题的方法。怎样使数学课堂充满生机和活力？怎么使学生喜爱数学并激发其创意和探索精神？经过培训学习，初步找到了数学教学中存在的问题：教师在备课时更多的是考虑自己怎么“教”，而很少考虑学生如何“学”。现在，教师的教学观念和教学习惯需要改变。我们应更多地思考学生如何‘学，以“为学习而设计、为学生发展而教”。

一、改变教学形式，重视数学活动

在四边形内角和定理的教学中，让每位学生任意画一个四边形，然后用剪刀剪下来，再把它的四个角也剪下来拼在一起，问学生发现了什么？学生通过动手操作发现四边形四个内角拼在一起等于一个圆周角即360°，最后再引导学生进行说理论证。在讲四边形的外角和时，在教室后面宽敞的地方任意画一个大四边形（如下图）。让一个学生从点O出发转∠1至点A，再转∠2走至点B，转∠3走至点C，转∠4走回至点O。问学生发现了什么？学生发现刚好转了一圈，感性认识到四边形四个外角之和是360°。在多边形外角和定理的教学时，也让学生以这种方式去理解。通过开展数学活动，让每一个学生都参与数学，有利于激起学生的探索热情、养成学生的探索习惯、培养学生的探索能力。

二、创设问题情境，激发学生求知欲

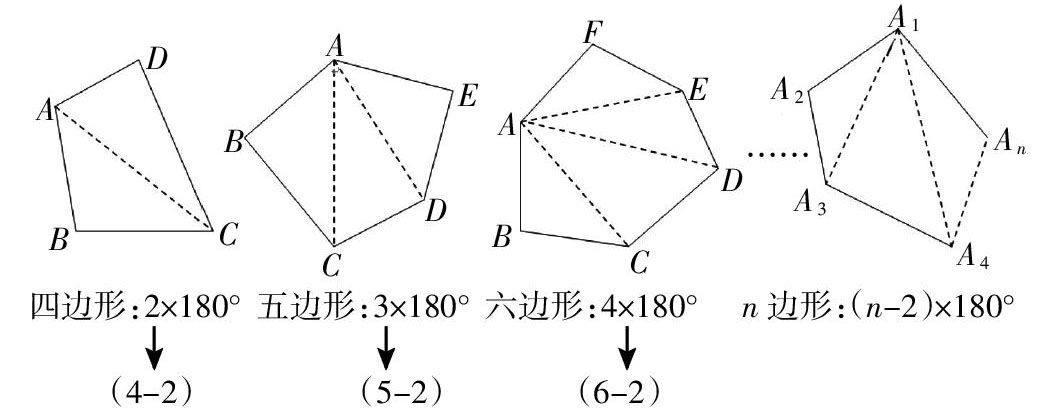
在多边形内角和定理的教学时，作如下设计：按顺序画出四边形、五边形、六边形、……n边形，并经过这些多边形的一个顶点作出它的所有对角线（如下图）。

问：四边形的内角和等于多少度？五边形的内角和等于多少度？六边形呢？……n边形呢？学生通过探索发现：经过n边形的一个顶点作n边形的所有对角线，可作（n-2）条对角线，这些对角线将n边形分成了（n-2）个三角形，因此n边形的内角和等于这（n-2）个三角形的内角和即（n-2）×180°。在这个过程中，让学生体会到由简单到复杂、由特殊到一般的思维过程，同时也领悟到化归的思想，把多边形问题转化为三角形问题。再用下面两个问题来帮助学生进一步理解多边形内角和定理及化归思想：（1）在多边形内部任取一点0，将点0与各顶点连接，得几个三角形？n边形内角和怎样计算？（如下图）

三、运用现代教育技术手段和直观教具，提高学习效果

在平行四边形及其性质的教学中，制作课件，利用多媒体手段使图形动化，让学生观察。问：什么是平行四边形？然后启发学生从平行四边形的边、角、对角线等方面去思考。经过观察、思考和讨论，从而得出平行四边形的性质，再让他们进行说理证明。

在“梯形”的教学中，为使学生理解作辅助线的方法，教师准备一些梯形硬纸片（大小不相等）和一个小三角形硬纸片，让学生观察。并提出问题：（1）能把梯形分成两个三角形吗？（2）能把梯形分成一个平行四边形和一个三角形吗？（3）能把一个梯形分成一个矩形和两个三角形吗？（4）要把梯形变成一个大的三角形，怎么办？教师可提示：在梯形的上底拼上一个小三角形，试试看。学生通过动手操作很快回答出了上述问题。这些问题为学生后面学习等腰梯形的性质和判定作了很好的铺垫，也为证明有关梯形几何题作辅助线的方法有了一定的理解。运用现代教育技术手段和直观教具，有利于培养学生的观察能力，加深学生的感性认识。

四、鼓励合作学习，培养创新能力

在三角形和梯形的中位线定理的教学中，事先准备好若干三角形、梯形硬纸片和若干把剪刀。给各小组的问题是：你能把一个三角形剪去一个内角拼成一个平行四边形吗？你能把一个梯形剪去一个内角拼成一个三角形吗？如何剪怎样拼？看哪一组先完成任务。各小组各抒己见，共同合作，每个组都有自己与众不同的答案，每个小组派代表抢答。各小组将所剪拼图形贴到黑板上或墙上，剪拼方法有若干种（如图）。表扬优先完成任务者。然后进行说理论证，这种方法能激发学生的学习兴趣，提高学习的积极性和创造性。

图1沿中位线DE剪，把△ADE绕点E旋转至△CEF位置得平行四边形DBCF

图2沿AE剪，点E是CD的中点，把△AED绕点E转动180°到△FEC得△ABF

图3沿中位线EF剪，把梯形AEFD绕F转动180°到HGFC的位置得平行四边形BHGE

五、教给学习方法，提高学习效率

每门学科都有其自身特点和思维方法。数学也是如此，教师要教给学生学习方法和思维策略。如：在四边形的教学中，教学重点是特殊四边形的定义、性质及其判定，而性质又是通过对四边形的边、角、对角线等的研究与分析获得的。特殊四边形的判定又恰好是其性质的逆命题。因此，学习四边形，要抓住四边形的边、角、对角线及其性质、判定这一关键来学习。掌握了学习方法，学习效率会大大提高。教学生学以致用。如：（1）四边形的不稳定性在日常生活中有什么用，请举一些例子；如何克服四边形的不稳定性？（2）形状、大小完全相同而不规则的四边形可以用来镶嵌地板吗？为什么？让学生剪一些硬纸片亲自实践一下。（3）工人师傅在做门框或矩形零件时，常用测量平行四边形的两条对角线是否相等来检查直角的精度，这是根据什么道理？（4）如何利用三角形中位线定理来测量池塘的长度？（5）怎样计算人字形梯子横档的长度？学生在学中用，在用中学，就能进一步理解和巩固所学知识。

总之，数学教学要以学生主动发展为宗旨，充分考虑学科特点、学生学习特点、认知规律和年龄特点，积极开展数学活动，让学生在活动中、在动手操作中学会数学知识；在直观形象化教学中获取数学知识；在学以致用中理解和巩固所学知识……这就要求教师认真学习新的教育思想，改变教学观念和教学行为，认真分析研究课程，整合教学资源，精心设计教学，使教学更符合学生认知特点和规律，以不断促进学生主动地学习发展。

参考文献：

奚定华.数学教学设计.华东师范大学出版社，2001-01.

（作者单位 云南省双江县第一完全中学）