从“流于形式”到“指向实质”

叶柱

解决问题是小学数学课程实施的重要内容。现行教材改变了以往教材“应用题块状聚集”的编写模式，除了安排极少数的专题单元，绝大部分解决问题的教学内容均与“数与代数”（尤其是数的运算）教学内容有机融合。需要明确的是，这并不意味着新教材对解决问题关注程度的削减与弱化，而是更为充分地体现出解决问题“算用结合”的现实意义。《数学课程标准》（2011年版）在“课程目标”中明确指出：“通过义务教育阶段的数学学习，使学生能……增强发现和提出问题的能力、分析和解决问题的能力。”从中，对当前解决问题的教学提出了由先前的“两能”（分析问题、解决问题的能力）向当下的“四能”（发现问题、提出问题、分析问题、解决问题的能力）良性提升的更高要求。反观教学现实，客观地说，很多老师都很重视解决问题的教学组织，但其中暴露的某些现象也应引起我们的深层叩问。

1.“发现问题”是否有空间

我们常说的“发现问题”，并非仅指“想到一个数学问题”，而是涵盖“洞察情境所含的各种信息及其联系、进而生发相关问题”的过程性意蕴。由此，笔者认为，“发现问题”的核心要素是“信息解读”。日常教学中，我们常能看到如下场景：呈现一幅主题图后，教师随即发问，让学生口述“从图中发现了什么信息、想到了什么问题”。主题图大多素材鲜活、信息多元，由于缺乏必要的读图时间，学生发现的信息往往是缺损的，学生提出的问题常常是浅层的。出示一道数学题后，教师要么抽一位学生代表读题，要么干脆跳过读题环节，快速切入解答活动。表面上，时间省了。实际上，由于学生对问题信息的卷入不足，效果差了……长此以往，当学生独立面对一个数学问题时，他对信息解读会有一种“浅尝辄止”“蜻蜓点水”“自以为是”的“条件反射”，从而严重影响解决问题的实际效果。

2.“提出问题”是否有价值

大家已有共识：提出问题比解决问题更重要。近年来，很多教师都已重视“提出问题”的有关教学。不过，要警惕“标签化”倾向。前段时间，笔者听了一节《小数加减法》（人教版四年级下册），教师借助课件出示教材主题图（如下图）后，脱口而出：“大家能提出什么数学问题？”学生轻而易举地提出了“相差几分”的问题。这个环节，看似没有任何纰漏。但静心反思，根据这幅主题图所蕴含的信息，还能提出其他数学问题吗？似乎没有了，“求和”显然没有意义。在这样的教学活动中，“提出问题”有点类似于语文课中的“看图说话”，其数学价值无法得以最大化体现。所以，重视“提出问题”的教学，并非贴上“你能提出什么问题”的标签就够了，我们更应关注“如何让提出的问题更有价值”。

3.“分析问题”是否有深度

以往的应用题教学中，很多教师拥有一套极富操作力的思路分析教学策略，如“解决这个问题，我们需要知道哪些条件”的“分析法”，如“根据这些条件，我们可以解决哪些问题”的“综合法”……基于新课程理念的解决问题，注重了素材情境的现实化、数学信息的多元化及解决策略的个性化，对“分析法”“综合法”等思维策略相对淡化。于是，我们看到，“分析问题”成为了“隔靴搔痒”。笔者执教《用连乘解决问题》（人教版三年级下册）时，学生列出例题“一个方阵，每行5人，有8行。三个这样的方阵共有多少人”的算式“5×8×3”后，请其解释“为何求一个方阵人数要5乘8”？有学生说：“因为5是每行5人，8是有8行，所以用乘法。”有学生说：“求一共要用乘法。”还有学生说：“用乘法比较简便。”不能说这些学生的回答毫无道理，但显然离“因为求8个5，所以用乘法”的数学本质还有一段距离。对此，如若教师熟视无睹，那就有失引领之职了。

4.“解决问题”是否有侧重

很多时候，解决问题的策略通道是多样的，这也是“解决问题”区别于“应用题”、充分体现“不同的人在数学上得到不同的发展”的重要方面。因此，“算法多样化”便成为了解决问题教学过程中的常见风景。然而，很多教师过分追求解题策略的多样性，但对每种策略仅是点到即止，缺乏扎实的本质挖掘。这样一来，解决问题常常显得“轰轰烈烈”且“飘忽不定”，部分学生在由衷感叹“方法真多”的同时，并没能学到多少真正能够发挥长效的策略思想。笔者认为，对班级团队而言，确实需要依托“算法多样化”来发散思维、分享智慧、共同成长。但对学生个体而言，与其忙忙碌碌且蜻蜓点水般地触摸多种策略，不如安安静静且深层聚焦地建构一种策略。

从以上四个侧面中，我们不难发现当前解决问题教学存在的“形式化”误区。显然，只有作为教师的我们深刻领会了“发现问题”“提出问题”“分析问题”“解决问题”这“四能”理念的要义，并立足实践，理性超越“形式化”，切实探求“实质性”，解决问题教学方能提升效度。为此，笔者提出四条行动建议，以抛砖引玉。

一、丰富表征体验，让“发现问题”更充分

观察需要时间，审阅依赖空间。在解决问题的初始阶段，教师务必控制自己“急于出手”“贪快求多”的冲动，给学生留足必要时间、提供合适空间，使其能够静心驻足、充分感知，将问题信息有效纳入脑海之中，从而优化解决问题的“第一印象”。除此之外，教师更要通过自己有意识的常态训练，帮助学生逐步形成“有效审题，增强表征”的学科基本功。

1.着眼细节，培养审题习惯

根据笔者的实践经验，教师可按年段、有侧重地培养学生的审题（图）习惯。其一，低年级着重培养“读完整”的审题习惯。教师可通过“谁能完整地说说图上有哪些信息”“除了左边的信息，右边还有什么信息”“还有补充吗”等即时追问，强化学生的“信息卷入”意识。其二，中年级着重培养“读细致”的审题习惯。引导学生切实关注问题信息中的重点词句（可标注圈画），突出要点，直面关键。其三，高年级着重培养“读反复”的审题习惯。要求学生不仅在解决问题前认真读题，更要在解决问题后再次读题。

另外，解决问题过程中，教师还应基于现场学情，注意对审题习惯的细腻养成。

2.依托图示，提升表征能力

审题过程中，多让学生用语言描述“这道题已知什么、要求什么”，是一种较为常用且行之有效的信息梳理方式。除此之外，我们还应重视“几何直观”的思想渗透。也就是说，从低年级开始，教师可有意识地引导学生“用自己喜欢的图示来描述问题含义”。图示，不苛求规范性，而关注实用性，重点在于引导学生把自己审题时的所见、所感、所想真实而鲜活地表达出来。这个图示形成的过程，既是透视情境的过程，更是凸显本质的过程，具有十分重要的数学价值。举个例子，有一类倍数问题，如“钱塘江全长约605千米，比曹娥江的3倍还多59千米。曹娥江全长多少千米？”学生错误率常常偏高。如果学生能够带着“几何直观”的强烈意识，通过简洁图示，整理问题信息，那么，无论是“算式法”还是“方程法”，正确率或会更高。

二、加强有序训练，让“提出问题”更扎实

人教版教材中编有很多主题图，在其中再现了现实场景，融会了丰富信息。这样安排的意图是，使学生能在丰富资源的全面解读中，逐步理顺思维线索，进而产生问题需求。那么，教师在依托教材主题图、培养学生提出问题的能力的过程中，需要注意什么呢？

1.由扶到放

出示主题图后，教师不要一味追问“你能提出什么问题”，而应根据学生需要，对提问策略有所指导。低年级时，教师可在学生解读信息后，提问启发：“根据……和……等信息，你能提出什么问题？”使学生感觉到，有效地提出问题是基于具体信息的。久而久之，他们便会形成一种“先获取信息、后审思逻辑、再提出问题”的策略意识。而这，对其提出问题能力的提高至关重要。到了中高段，教师可逐渐放手，要求学生自主完整地表述“根据……和……等信息，我提出的问题是……”另外，在组织学生提出问题时，尽量避免“信息标准”“问题单一”，而应尽量追求“信息多元”“问题丰富”，使学生在富有开放性的问题情境中锤炼思维、提升能力。

2.面向全体促落实

我市曾连续三年组织解决问题质量调测。就提出问题的现状看，学生所提问题“无意义”“表述冗长”“词不达意”的不足显而易见，这从一个侧面反映了常态教学的客观缺失。很多时候，教师只是把提出问题作为引出列式、启动计算的“幌子”，因而，不够重视提出问题的教学组织。然而，当提出问题作为数学课程的重要目标时，显然每位学生都必须拥有提出问题的学科功底。所以，组织学生提出问题时，不能只让个别学生口头表述，而应该让全体学生人人参与，且有一定比重的书面表达。由此，提出问题的教学组织才能落到实处、惠及全班。

三、挖掘数学本质，让“分析问题”更到位

数学课程视野中的解决问题，其本质是依托现实情境、应用数学知识。作为解决问题重要环节的“列式”，是以四则运算的数学意义为依据的，因此，众多有识之士一直倡导“夯实运算意义的理解、为解决问题坚实奠基”，显然很有道理。除此之外，我们还要引导学生透视情境表象，把握问题结构。于是，数量关系便成为不可或缺的逻辑拐棍。

1.链接运算意义，夯实细节算理

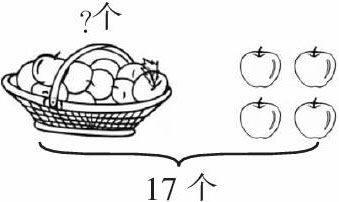
究竟用哪种运算来列式，显然要看信息之间的相互关联暗合了哪种运算的本质含义。比如，一年级认识“减法”时，有类题目（如下图）学生经

常出错，把“17-4=13”列成“13+4=17”。对此，教师总会强调：总数知道了，该用减法；求总数，才用加法……但效果似乎并不明显。实践证明，教师应组织学生仔细看图、充分描述，进而积累以下经验：一共有17个苹果，右边数出了4个，左边还剩下几个？这道题所求的，是17里面去掉4后还剩余的数，所以该用减法。这样的教学，回到了减法运算的意义原点，容易使学生心服口服、产生认同。此后，凡是遇到“求剩余”的问题，学生便能自然选用减法，而不至于瞎猜。

2.依据数量关系，把握整体结构

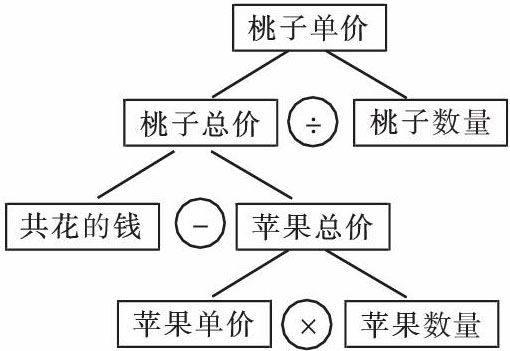
《数学课程标准》（2011年版）指出：“（使学生）在具体情境中了解常见的数量关系，并能解决简单的实际问题。”简短的阐述，点明了数量关系对解决问题的重要作用。事实上，无论多么复杂的数学问题，都蕴含着一组或多组数量关系。比如，在“妈妈买来5千克苹果和4千克桃子，一共用去了73.8元，每千克苹果9.8元，每千克桃子多少元？”这道题中，就隐藏着三组基本的数量关系（如下图）。从上往

下看，从问题出发，通过数量关系，找到条件，逐步推进；从下往上看，从条件出发，通过数量关系，引出问题，依次延续……解决问题教学中，如果能够经常引导学生依据数量关系“抽丝剥茧”“顺藤摸瓜”，那么，既能提高解题效率，还能增强分析能力。因此，一方面，教师要注重基本数量关系的教学引导，使学生在理解术语的基础上把握关系；另一方面，教师还需坚持组织学生立足数量关系、剖析问题思路，不松懈，不浮夸。

四、积累活动经验，让“解决问题”更有效

对学生而言，通过解决问题的学习活动，不仅需要得到“鱼”（实现某道题目的顺利解答），同时还应学会“渔”（掌握解决问题的可靠策略）。正如新课标强调的：“（使学生）获得分析问题和解决问题的一些基本方法……”所以，在解决问题的教学中，教师既要夯实每次活动的体验过程，让学生能够“深入进去”，自主探寻解决问题的思路。同时，还要注重每个阶段的经验提炼，让学生能够“超脱出来”，逐步积累解决问题的经验，如“有效审题的经验”“画图示意的经验”“有序分析的经验”“代入检验的经验”，等等。这些经验，会纳入学生主体的解决问题素养系统，并将对其今后发现问题、提出问题、分析问题、解决问题产生积极作用。

另外，除了注意策略提炼，教师还应给学生提供内化经验、迁移经验、运用经验、提升经验的机会，在足量的“基本训练”之后，引导学生在变式情境中进行“拓展历练”。