基于模糊化符号复杂度的脑电运动想象识别算法*

周光省，罗志增，高云园

(杭州电子科技大学机器人研究所，杭州310018)

脑机接口BCI(Brain Computer Interface)是不依赖于大脑外周神经与肌肉组成的正常输出通路的控制系统［1］。基于脑电的BCI技术，把脑电信号转化为对外界的控制信号，实现了人脑控制信息与计算机等外设间的交换。脑电信号是脑神经细胞电生理活动在大脑皮层或头皮表面的总体反映。脑电信号的特征提取是BCI系统中一个重要的环节，是进行分类、正确解读大脑意识任务的关键。

脑电信号特征提取方法主要包括单一的时域或频域分析［2］、时频分析［3］、非线性动力学方法［4］等。在时频分析方法中比较典型的是小波变换方法。当使用较小尺度时，时轴上观察范围小，而在频域上相当于用较高频率做分辨率较高的分析;当使用较大尺度时，时轴上观察范围大，而在频域上相当于用低频小波作概貌观察。季忠［5］采用小波变换法处理脑电信号时，在时域、频域都具有表征信号局部特征的能力。因为脑电信号是非线性非平稳的时间序列，时域和频域分析方法以及时频结合的分析方法均不可避免存在局限性。考虑到脑电信号的混沌特性，非线性动力学方法具有非周期性、非随机性、非线性等特点，非线性动力学方法成为了脑电信号处理的热点研究课题［6］。

近年来，李亚普洛夫指数、关联维和复杂度为较常见的非线性动力学方法。Lempel-Ziv复杂度是一种非线性动力学特征参数，可以用来刻画有限序列和随机序列的相似程度，能够从一维的角度反映时间序列，所需数据较短。又，事件相关同步/去同步ERS/ERD (Event-related Synchronization/Eventrelated Desynehronization)［7］，被认为脑电信号与肢体运动想象间具有很大关联性的研究方法。文献［8］已证明二值化Lempel-Ziv复杂度可以很好的反映ERD/ERS现象，且想象左右手运动时，同侧电极复杂度减少，对侧电极复杂度增加，和脑电信号幅值变化恰好相反，但结果确定性强。

作为特征值的Lempel-Ziv复杂度计算，其关键是原始信号粗粒化。传统粗粒化算法即二值化处理，易致区间内部细节变化无法在二值化后的序列中体现出来。细粒化度量法［9］则犹如复杂性度量上的“显微镜”，细粒化指数就如“放大倍数”。模糊理论作为一门重要的数学分支，用数学的方法对现实世界的问题进行了模糊性和不确定性研究。在模糊理论的研究基础之上，Chen等人［10］将模糊理论应用于生理电信号序列复杂度测度之中，提出了使用模糊熵作为医学生理电信号的特征测度标准，取得了很好的效果。本文在脑电信号的复杂度细粒化多符号度量中引入模糊算法，提出的模糊化符号复杂度既保留了二值化Lempel-Ziv复杂度算法的优点，又弥补了其“粗”的缺陷，以脑电信号的ERD/ERS现象为研究对象，模糊化符号复杂度作为脑电信号的特征值，进行左右手运动想象脑电信号分类研究。研究结果表明，模糊化符号复杂度的平均分类正确率高于二值化Lempel-Ziv复杂度算法。

1 模糊化符号复杂度算法

1.1 复杂度的细粒化多符号度量

在不同的场合和条件下，复杂这个词所指的具体含义是不同的。对复杂性的度量经常伴随着对系统的粗粒化和符号化。符号的描述需区分不同的层次，复杂是相对的、有层次的。

目前最常用的粗粒化方法是对原始信号进行二值化处理。先对序列求平均值，大于平均值的赋1，小于平均值的赋0，将原始信号转化为符号串再计算其复杂度。上述二值化方法存在着一定的缺陷，原因是它忽略了幅值的变化，仅考虑频率的变化。对深度睡眠状态下的脑电信号(Electroen-cephalogram，EEG)进行粗粒化，结果就会发现重构后的二值化序列为(1111…1，0000…0…)。显然，这是一种极规则的形式，与实际序列本身的动力学特性不符，这种现象称之为“过分粗粒化”。文献［11］提出了分析混沌伪随机序列复杂度的模糊熵算法。符号序列的细粒化方法的提出，使得复杂性度量不仅适于长序列也适于短序列。

1.2 模糊隶属函数构造

令x为非负整数，设A是论域x到［0，1］上的一个映射，即

其中论域x为不同维数度量两值之间相差大小的集合，A(x)称为模糊集X上的隶属函数。构造序列复杂度测度的模糊隶属函数是一个正规模糊集。本文采用sigmoid型隶属度函数，其表达式为:

参数x用于指定变量的论域范围，a和c决定了sigmoid型函数的形状，x为当前点x(i)和该点之后的n个点{x(i+1)，…，x(i+n)}依次相减的差值得到n个变量构成数组。嵌入维数n称为细粒化指数。选取 a=1，c=0，n=2，x分别取 x(i)－x(i+1)和x(i)－x(i+2)返回得到二维的函数值矩阵。当x＜0时，y 取值区间为(0，0.5);当 x=0 时，y=0.5;当 x＞0 时，y取值区间为(0.5，1)。

1.3 模糊化符号复杂度

计算Lempel-Ziv复杂度的关键是对原始信号进行粗粒化处理，按序号连续顺序组成的一维时间序列为{x(i)|i=1，2，…，n}，长度为n的时间序列中，采用二值化方法对进行重构，令

式(3)中xave为原序列的平均值，用{S(i)|i=1，2，…，n}记x(i)重构后的符号序列。当i取遍1，2，…，n时，原序列中的元素x(i)＜xave时，S(i)赋符号0，否则赋符号1，由此建立符号序列S(i)。

对运动想象脑电信号的模糊化符号复杂度处理方法如下:

以时间序列中的当前点x(i)作为阈值，而不是以时间序列的平均值作为阈值。通过变换阈值的参照，把每一个当前点x(i)作为相对参照点，而不是把平均值作为绝对参照点。本文取n为2，通过脑电信号时间序列中当前点x(i)和该点之后的2个点{x(i+1)，x(i+2)}依次相减得到

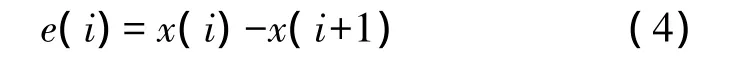
以及

将e(i)和ec(i)输入到sigmoid型隶属度函数，通过逻辑判断得到多种情况，根据返回的函数值y(i)和yc(i)分别划分为“正大”、“正小”、“零”、“负小”、“负大”，再将 y(i)和 yc(i)分别组合得到5×5种情况，分别记为不同的符号，一共由25个符号表示，由此建立多符号序列S(i)，进行多符号度量得到模糊化符号复杂度。上述的模糊化符号复杂度方法适用于包括周期序列在内的任意序列。细粒化指数取2，用Lempel-Ziv复杂度算法处理多符号序列S(i)，得到模糊化符号复杂度。

2 运动想象脑电信号的特征提取

2.1 实验数据

所用的实验数据来自公开发布的用于BCI2003竞赛的标准数据Data setⅢ，由奥地利Graz大学提供。实验是由一个含有反馈信号控制的在线BCI系统完成，受试者坐在舒适的椅子上，每一个实验段为9 s。在每个实验段的前2 s内，受试者保持休息状态;在第2 s时显示器上出现一个十字光标同时伴随一个声音信号提示受试者准备开始想象任务。在第3 s时，十字光标由一个指示左右方向的箭头代替，要求受试者根据箭头方向想象左手或右手运动，第4 s时BCI系统对两种意识任务进行在线分类，随后根据前1 s记录的脑电信号AAR系数参数结合判别式分析得到的分类结果提供给受试者一个反馈信号，使其继续完成想象相应手运动的任务，直到第9 s实验完成。

实验数据包括分别想象左、右手运动意识任务各70次实验的训练样本及测试样本数据。所有实验由7组，共280次实验组成。实验采用三电极方式采集，分别选择位于C3、C4、Cz三个电极前后各2.5 cm位置记录脑电。当人们想象肢体运动时，大脑的感觉运动皮层会表现出脑电的节律性活动［12］。C3、C4相当于大脑感觉运动区，反映了受试者在想象左右手运动时大脑状态变化的最有效信息。而Cz电极位于辅助运动区附近，也会随着运动想象而出现去同步现象。脑电的采样频率为128 Hz，利用0.5 Hz～30 Hz带通滤波器进行滤波。

2.2 实验结果与分析

为了验证模糊化符号复杂度的运动想象脑电信号特征值能很好的反映ERD/ERS现象，对脑电信号做如下处理:首先从单次实验流程的第1 s开始，以1 s长度为时间窗，计算该采样点前1 s时间C3、C4脑电信号的模糊化符号复杂度，每次移动窗口1个采样点，直到计算出最后1 s的模糊化符号复杂度为止，然后将同一运动想象任务的所有试验的模糊化符号复杂度叠加平均，得到受试者的平均模糊化符号复杂度序列。

从图1可以看出，在t=3 s～5 s附近，受试者在想象左手运动时，同侧的C3电极的平均模糊化符号复杂度明显减小，而对侧的C4电极的平均模糊化符号复杂度明显增加;从图2可以看出，在t=3 s～4 s附近，受试者在想象右手运动时，同侧的C4电极的平均模糊化符号复杂度明显减小，而对侧的C3电极的平均模糊化符号复杂度明显增加。由此可见，模糊化符号复杂度能很好的反映ERD/ERS现象。

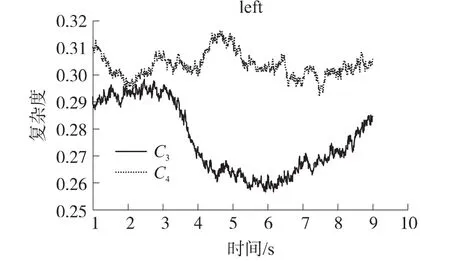
图1 想象左手运动时，C3、C4脑电信号的平均模糊化符号复杂度时间序列

图2 想象右手运动时，C3、C4脑电信号的平均模糊化符号复杂度时间序列

为了和模糊化符号复杂度作比较，计算了以二值化复杂度作为脑电信号特征值的结果。从图3可以看出，在t=3 s时，受试者在想象左手运动，同侧的C3电极的平均二值化Lempel-Ziv复杂度减小，而对侧的C4电极的平均二值化Lempel-Ziv复杂度增加;从图4可以看出，在t=3 s时，受试者在想象右手运动，同侧的C4电极的平均二值化Lempel-Ziv复杂度减小，而对侧的C3电极的平均二值化Lempel-Ziv复杂度增加。平均二值化Lempel-Ziv复杂度与模糊化符号复杂度变化规律基本一致，但后者比前者明显，其ERD/ERS现象更为突出。

图3 想象左手运动时，C3、C4脑电信号的平均二值化Lempel-Ziv复杂度时间序列

图4 想象右手运动时，C3、C4脑电信号的平均二值化Lempel-Ziv复杂度时间序列

2.3 特征向量构造

受试者在分别想象左、右手运动时，对应的C3、C4电极反映了大脑状态变化的最有效信息，Cz电极位于辅助运动区，也会随着运动想象出现去同步现象，属随动性去同步现象，若考虑C3、C4分别与Cz的差，能有效降低特征中的噪声。因此，为了能够突出想象左、右手运动时，大脑半球两侧初级感觉运动区相对于辅助运动区脑电模糊化符号复杂度的差异，构造特征向量如下:首先分别计算C3、C4和Cz电极位置所对应的脑电模糊化符号复杂度Kc3，Kc4和Kcz，然后分别计算Kc3、Kc4和Kcz的复杂度差值，得到脑电模糊化符号复杂度差值Kc3z，Kc4z将其组合二维特征向量(Kc3z、Kc4z)用于后续大脑意识任务的分类。

2.4 意识任务分类识别

SVM是基于统计学习理论的方法，能较好的解决小样本、非线性、高维数等问题。它通过适当的非线性映射将输入向量映射到一个高维的特征空间，使得数据总能被一个超平面分割。本文采用径向基函数RBF(Radial Basis Function)作为SVM的核函数，对想象左右手运动的脑电信号进行分类识别。RBF核函数的表达式如式(6)所示。

支持向量机分类器的性能主要与惩罚因子C以及核函数中的参数变量γ的取值相关。常见的选取最优参数的方法为交叉验证，采用网格划分的方式进行参数调整，同时将数据分为训练集和测试集两种。设定惩罚因子C和核参数γ的范围均为［0.1，100］，利用训练集中的样本数据训练SVM模型，并将交叉验证分类准确率作为适应度函数，设置精度条件均方差的临界值为0.1。采用十折交叉验证，即将数据集分成十份，轮流将其中9份作为训练数据，1份作为测试数据，进行试验。每次试验都会得出相应的正确率。10次的结果的正确率的平均值作为对算法精度的估计，最终选择分类准确率最高的参数组合作为最终的SVM分类器的模型参数。

实验过程中，受试者执行运动想象的任务是从第3 s开始，以3 s～9 s各典型时段的运动想象脑电信号的模糊化符号复杂度作为特征向量进行识别分析，并和二值化Lempel-Ziv复杂度进行对比，结果如表1所示。

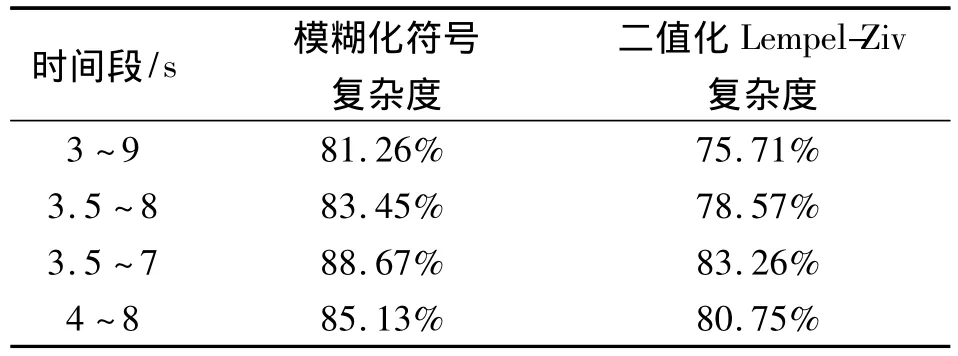
表1 各典型时段的运动想象脑电信号平均分类正确率

观察表1，在3.5 s～7 s内，脑电信号的模糊化符号复杂度的平均分类正确率最大达到88.67%，而二值化Lempel-Ziv复杂度的平均分类正确率最大为83.26%，前者的平均分类正确率要高于后者。在其他典型时段内，模糊化符号复杂度分类正确率均高于二值化Lempel-Ziv复杂度。实验结果表明，以SVM分类器作为验证手段，基于模糊化符号复杂度的运动想象脑电信号特征的平均分类正确率要高于二值化Lempel-Ziv复杂度为特征的分类方法。

3 结论

脑电信号的特征提取的目的就是将记录的脑电信号转换为能表达不同意识任务的特征向量，从而为分类器提供最优的输入。本文以ERD/ERS现象的模糊化符号复杂度作为脑电信号的特征值对左、右手运动想象任务进行分析。模糊化符号复杂度是在细粒化多符号度量中引入模糊算法，反映出信号一定程度范围内的变化过程，可以把时间序列分成多个区域，使得细节变化可以在符合化序列中体现出来，弥补了粗粒化算法处理的缺陷。实验结果表明，模糊化符号复杂度能很好的表征左右手运动想象时的EEG特征变化，比二值化Lempel-Ziv复杂度算法更有区分度。模糊化符号复杂度可以很好地作为左右手运动想象时的脑电信号特征，为意识任务的分类提供很好的依据。因此，模糊化符号复杂度是一种良好的特征信号处理改进方法。

［1］ Wolpaw J R，Birbaumer N，Heetderks W J，et al，Brain-computer Interface Technology:A Review of the First International Meeting［J］.IEEE Transactions on rehabilitation Engineering，2000，8(2):164－173.

［2］ 黄思娟，吴效明.基于能量特征的脑电信号特征提取与分类［J］.传感技术学报，2010，23(6):782－785.

［3］ Milan J R，Mourino J.Asynchronous BCI and Local Neural Classifiers［J］.IEEE Transactions on Neural Systems and Rehabilitation Engineering，2003，11(2):159－161.

［4］ Wang Xingyuan，Luo Chao，Meng Juan.Nonlinear Dynamic Research on EEG Signals in HAI Experiment［J］.Applied Mathematics and Computation，2009，207(1):63－74.

［5］ 季忠，王巧兰，秦树人.基于小波变换的脑电噪声消除方法［J］.重庆大学学报，2005，28(7):15－17.

［6］ 范影乐，李谷，刘亚景.基于排列组合熵的脑电意识任务识别方法的研究［J］.传感技术学报，2008，21(1):74－78.

［7］ 吕俊，谢胜利，章晋龙.脑－机接口中基于ERS/ERD的自适应空间滤波算法［J］.电子与信息学报，2009，31(2):314－318.

［8］ 罗志增，曹铭.基于多尺度Lempel-Ziv复杂度的运动想象脑电信号特征分析［J］.传感技术学报，2011，24(7):1032－1037.

［9］ 柯大观，张宏，童勤业.格子复杂性和符号序列的细粒化［J］.物理学报，2005，54(2):534－542.

［10］ Chen W，Wang Z，Xie H，et al.Characterization of Surface EMG Signal Based OU Fuzzy Entropy［J］.IEEE Transactions on Neural Systems and Rehabilitation Engineering，2007，15(2):266－272.

［11］陈小军，李赞，白宝明，等.一种基于模糊熵的混沌伪随机序列复杂度分析方法［J］.电子与信息学报，2011，33(5):1198－1203.

［12］袁玲，杨帮华，马世伟.基于HHT和SVM的运动想象脑电识别［J］.仪器仪表学报，2010，31(3):649－653.