一种改进的边界节点检测算法*

张 姿，黄廷磊* ，吴拱星

(1．中国科学院电子学研究所，北京100190;2．桂林电子科技大学计算机科学与工程学院，广西桂林541004)

传感器网络是由大量节点组成的一种特殊的自组织网络，已经在军事监视、工业检测和医疗健康检测等领域得到了广泛的应用。近几年来，出现了作为自治设备的新型传感器节点，它集感知、处理、通信能力于一体，形成多跳传感器网络。实际应用中，大量传感器部署后，经常处于无人值守的状态[1－4]。因此，电池的损耗、动物的损坏、偶然事件的发生造成部分节点失效，便形成了空洞，影响网络的连通性。为了尽量减少空洞对网络连通的影响，准确识别空洞的边界，有助于保持数据业务流、防止数据损失，避免额外的能量消耗，防止空洞的扩展，并确定替代的通信路径。因此边界检测算法的研究具有非常重要的意义。

到目前为止，在无线传感器网络边界节点检测算法研究方面，许多学者已经进行了大量的研究工作，并且提出了许多有效的算法。根据算法使用的核心技术，可将目前的边界识别算法分为基于地理位置信息的算法、基于统计信息的算法和基于拓扑信息的算法[5－7]。本文主要研究基于拓扑信息的边界节点检测算法。

基于拓扑信息的边界节点检测算法利用网络的拓扑连接信息寻找隐藏的网络几何信息，从而确定网络节点的的分布。Ghrist等在文献[8]提出了一种基于拓扑信息的边界识别算法，算法利用节点同源且方向不可延续检测网络的洞。该种算法是比较有代表性的一种识别方法。但是该算法是集中式算法，不大符合传感器网络的应用发展。Olga Saukh等在文献[9]提出一种新的基于拓扑信息的算法。作者提供的算法没有过多的条件限制，具有比较普遍的应用价值。该算法通过寻找被取名为“flower”及“flower”的组合结构来检测网络的边界节点。算法的执行严格的依赖于“flower”结构。但是在某些特定应用场合，“flower”不总是存在的。针对实际应用，作者Funke等在文献[10]提出了一个非常有代表性算法，后续很多基于拓扑信息的边界节点检测算法都受该算法启发。该算法对节点度的要求比较高;为了获得比较好的检测效果，网络的平均节点度要求至少是15。Wang Yue等人在文献[11]提出了一种比较准确的检测算法，并且作者在论文中给出了算法可行性的理论证明。本文把文献[11]提出的算法简写为BRSN-TM算法。该算法虽然严谨但是执行了多次的网络洪泛以及整个网络节点的同步，所以造成网络节点通信量大。文献[12]对BRSN-TM算法进行了改进，设计了一种以网络纬度线检测网络边界的规模可扩展算法ABRSN-TM，但文中领导节点的选取方法过于简单，划分网络的纬度线的依据不合理，未描述如何将包围空洞的环转化为网络的内边界以及外边界。本文在文献[11－12]的基础进行改进，得到改进算法AIBNDA。

1 BRSN-TM算法

(1)构建最短路径树

在网络中选择一个节点作为最短路径树的根节点，命名为R节点。然后利用贪婪算法在网络中构建以R为根节点的最短路径树[11]。

(2)识别算法的“cut”节点对

网络中洞的分布信息隐藏在最短路径树的结构上。这个结构具体的说就是最短路径树上的“cut”节点对。“cut”的节点对是一对邻居节点，这对邻居节点的在最短路径树上的共同祖先节点明显比其他邻居点的共同祖先节点远。

(3)确定环

确定一个环，这个环包围网络中的洞。网络的一个包围洞的环是由“cut”的两个节点到达共同祖先的两条最短路径，加上“cut”两节点的连线组成。算法确定的这个环可以当成网络的内边界，只是这个内边界比较粗糙。但是已经基本具备内边界的特性。

(4)确定网络外边界和网络内边界

确定的环不会紧贴网络的内边界。作者通过对网络节点泛洪，重新求精网络的内外边界，从而达到准确识别网络的内外边界的目的。

2 AIBNDA算法

(1)选取领导节点

在AIBNDA中，领导节点是边界节点检测算法的发起节点并且领导网络中所有节点同步。ABRSN-TM中，领导节点的选取方法是以ID号最大节点作为领导节点，该方法实现简单。但是该方法的弊端是如果网络被某些不可预测的因素切断为连续性不明确的两个区域时，这样，选取的领导节点将无法启动两个区域的边界节点检测。为了避免这种选取方法的不足之处，因此AIBNDA采用竞争方法选取领导节点[13]。

(2)确定网络的信标节点

AIBNDA在网络中寻找两个信标节点，确定两个信标节点应具有两个特征:第一，两节点要起到信标节点的作用。第二，两节点应该位于网络中的某一方向相反的两端。所以充当信标节点的节点应该尽量跨越网络中的大部分特性区域。这里的特性主要指网络中洞的分布。通过领导节点L来寻找具有以上特性的两个信标节点。首先以领导节点L为信标节点，在网络中利用贪婪算法确定网络中每一节点到达L节点的最短跳数。然后选取到达L节点跳数最大的节点为信标节点，标号为N．同样的以节点N为信标节点，寻找到达节点N最远的节点，标号为S。从上面的方法可知，节点N和节点S满足信标节点的两个要求。

(3)划分网络的纬度线

在完成网络的信标节点选取后，网络中所有的节点同时已获取了自身节点到两个信标节点的跳数坐标。在网络中划分一些等距线，类似于地球上的纬度线，因此本文把这些等距线称为纬度线。纬度线为到达两信标节点的距离比值恒定的节点的集合。连续的纬度线定义为纬度线段，每段纬度线段上选取一个头节点，每个头节点代表纬度线段向领导节点发送一条注册消息。网络纬度线条数设定与纬度线间的间隔有关。ABRSN-TM是通过经验值，根据网络的规模，设定纬度线间的宽度。这种算法不够严谨，如果纬度线间的宽度比较大，有可能使网络中比较小的洞未能被检测出来(图1(a))所示。但是如果网络中纬度线间的宽度划分太小，使网络的纬度线比较密集，那么将增加网络的通信压力。如果希望比较准确的设置网络中纬度线的条数，可以先对洞的大小进行定义。然后利用洞的大小计算纬度线的条数，从而确定节点到达两信标节点的预设距离比值((图1(b))所示。网络中的纬度线的数量可用式(1)计算:

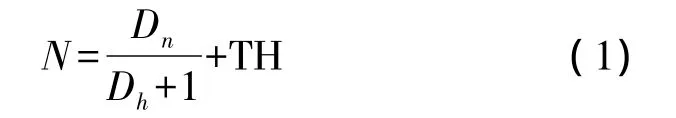
TH为纬度线加密系数，可取0、1、2等值，用于适当增加网络中的纬度线条数。Dh表示洞的直径定义为网络中洞的边界节点中相隔距离最大的两个节点之间的跳数。Dn表示网络中任意节点间距离最远的两节点的跳数距离定义为网络的规模。

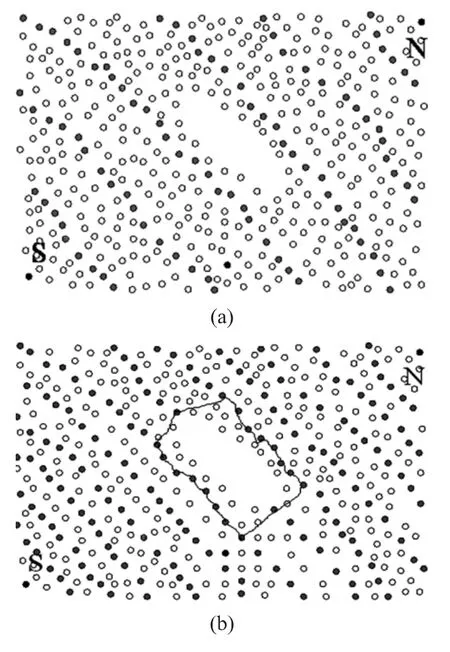
图1 网络中纬度线的划分

(4)确定网络中洞的分布情况

AIBNDA的核心思想是通过网络中洞的分布情况来寻找网络中包围洞的环。如果网络中存在洞，那么纬度线将被洞分割成多段;如果纬度线所跨越的地理区域不存在洞，那么纬度线将是连续的。把连续的整段纬度线，称为纬度线段。每段纬度线段上选取一个头节点，每个头节点代表纬度线段向领导节点发送一条注册消息。

节点ID值最小的节点被选为头节点，每个头结点发出包含自身ID及纬度线号的注册信息给领导节点。领导节点接收每个头节点的注册信息，并且对信息中的纬度线号进行计数。如果出现重复的纬度线标示符，那么说明该纬度线被网络中的洞切断。

(5)构造包围洞的环

根据Jordan曲线理论，二维平面内一条封闭的曲线把平面分成两部分:曲线内部和曲线外部。确定了网络中空洞的大概位置，就构造一个包围网络中空洞的环。这里所提及的环就是网络中由节点的连接组成的一条封闭的二维曲线。AIBNDA将构造的环把网络分成两部分:环内部为包围特定洞的部分;环外为不包含洞的部分。图2所示，网络中的空洞在纬度线3和纬度线7之间，同时也在纬度线4、5、6的两个头节点对之间。网络中的八个头节点，利用最短路径算法找到各自临近的头节点，将它们连接就形成了一个包围洞的环，命名为S。组成S的节点集合为{s1，s2，s3，……sn}。

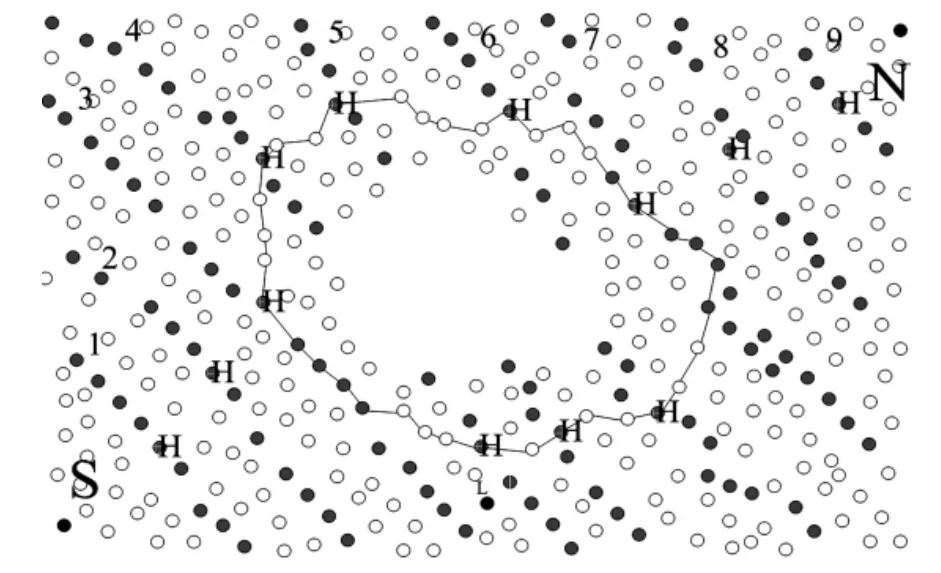
图2 网络包含洞的环

(6)识别网络内外边界

组成 S的节点集合{s1，s2，s3，……sn}。它们的一跳邻居节点集合分别是，Hops1(1)，Hops2(1)，Hops3(1)，Hops4(1)，Hops5(1)，…，Hopsn(1)。

随意选取S上的一个节点，假设s1，转发，Hops1(1)给它的所有1跳邻接节点。每个邻接节点找到自己1跳的邻接节点中，同时也是s1的1跳邻接节点的集合。总结如下:

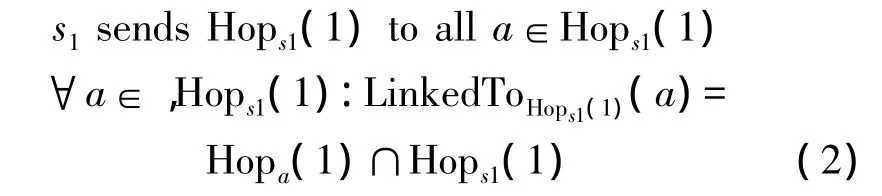
在式(2)中的LinkedToHops1(1)(a)是指在节点s1的1跳邻接表中同时也是节点a的1跳邻接节点的集合。为了演示这个算法，设已识别包围空洞的环为S3，图3所示。本文以s31为例。

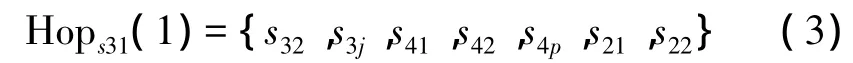
图3 包含空洞的环转换成网络内界的过程

表1显示了算法的运算过程。因为 s31、s32、s3j都属于环S3的节点，根据其邻居关系推出s41，s42，s4p是属于新环S4，s21，s22是属于新环S2。将S环上的其他节点依次按照上述步骤，就将形成完整的S4，S2。然后，将形成的 S4，S2，按照上述动态方法，形成新的环。在新形成的环，按照迭代方法，直到找到网络的内外边界，如图4所示。

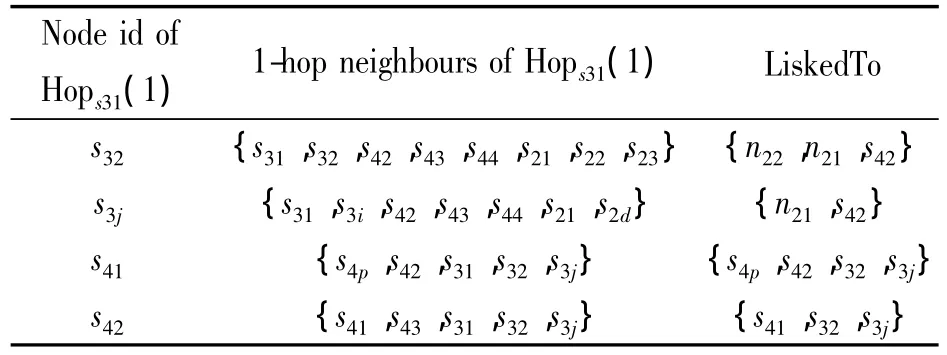
表1 S31的一跳邻居节点之间的相互通信的链接

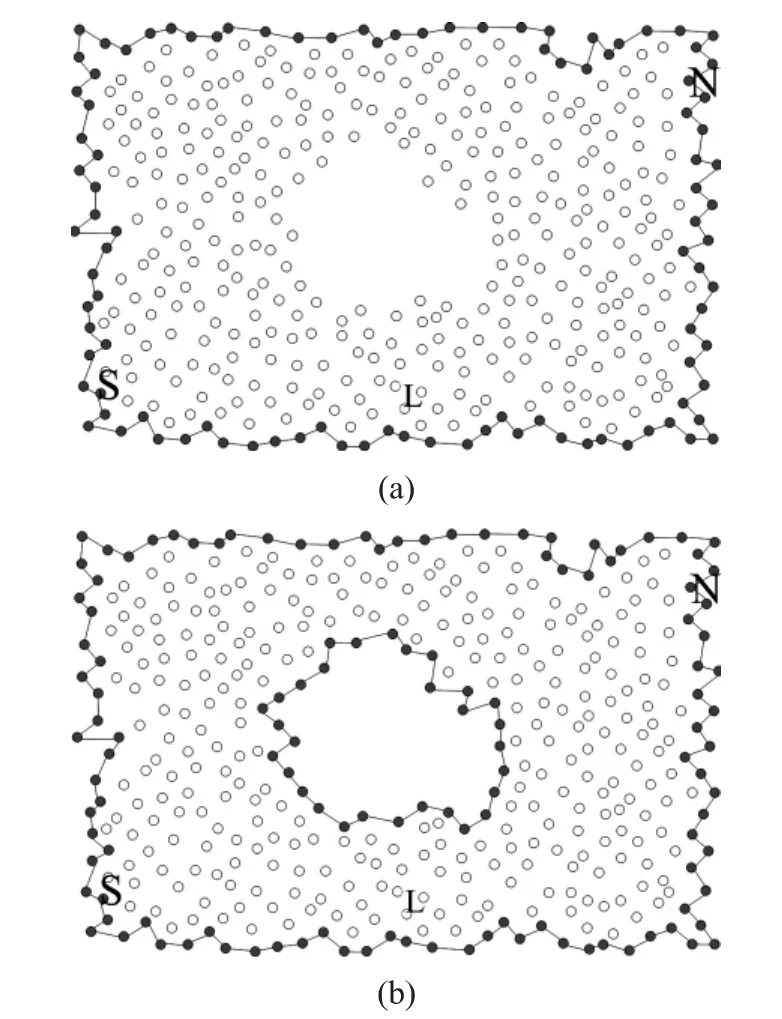
图4 网络的内外边界

3 仿真

为了验证AIBNDA的性能，用NS2进行了仿真实验[13]。在软件的环境中设置各种不同的参数验证算法的可行性。为了评估AIBNDA算法的优化性能，在统一的平台上对算法 AIBNDA、ABRSN-TM、BRSN-TM进行一系列的仿真，然后对比实验结果。实验过程中，网络的节点数、网络区域、节点通信范围、洞的类型、洞的数量等参数在未加说明的情况下采用如下初始值。节点数:3 500;网络区域形状:正方形;传感器区域规模:1 000 m×1 000 m;通信范围:30 m;平均节点度:9;洞的形状:类圆。

(1)节点度对算法检测准确率的影响

在这组实验中，通过调整网络中节点的数目，使节点的平均度在6、9、12、15变化。在不同节点度的环境下执行AIBNDA、ABRSN-TM、BRSN-TM算法各50次，分别记录边界节点识别的准确率，取平均值。

如图5，节点度为6时，算法AIBNDA、ABRSNTM、BRSN-TM边界节点的检测准确率都比较低。特别在BRSN-TM算法中，由于网络稀疏，从而致使稀疏区域的一些非边界的节点被误选为边界节点。算法ABRSN-TM中，由于缺少将包围空洞的环转化为网络的内边界以及外边界这一步骤，因此，边界节点的识别准确率不及ABRSN-TM。实验结果显示了随着节点度提高，边界节点检测算法的识别准确率不断的提高。从仿真结果可知，不管节点度高或者低，在识别准确率方面，AIBNDA分别比 ABRSNTM、BRSN-TM提高程度平均有2%和7%以上。因此在网络低节点度的情况下，AIBNDA拥有比ABRSN-TM、BRSN-TM更高的识别准确率。

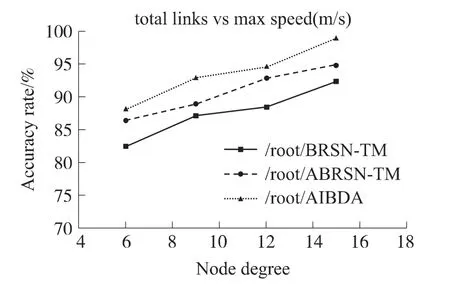
图5 不同节点度识别准确率

(2)洞的个数对通信量的影响

在这组实验中，网络中空洞的个数由1个变化到8个，AIBNDA、ABRSN-TM、BRSN-TM 算法各执行50次，分别记录算法的识别边界节点的通信量，计算平均值。图6所示，空洞的个数比较少时，BRSN-TM算法的通信量是比较少的。但是当网络的洞的个数大于3时，BRSN-TM的通信量超过了ABRSN-TM算法的通信量。当网络的洞的个数大于4时，AIBNDA算法的通信量低于ABRSN-TM算法的通信量。AIBNDA的通信量平均比ABRSN-TM、BRSN-TM低。所以，当网络的空洞大于4时，AIBNDA降低检测边界节点的通信量。

图6 算法交换的数据量

4 结束语

BRSN-TM算法以任意的节点为根节点，构造整个网络的节点拓扑最短路径树，利用包围网络中所有洞的环识别网络的边界节点。该算法虽然严谨但是执行了多次的网络洪泛以及整个网络节点的同步，所以造成网络节点通信量大。ABRSN-TM算法对BRSN-TM进行改进，但文中领导节点的选取方法描述不准确，划分网络的纬度线的依据不合理，未描述如何将包围空洞的环转化为网络的内边界以及外边界。本文针对BRSN-TM算法构造最短路径树的通信量大，ABRSN-TM算法的不足之处，从降低通信量及提高边界节点检测的准确性两个方面来考虑。在AIBNDA算法中，采用竞争方法选取领导节点，利用空洞的大小计算纬度线的条数，构造多个环分别包围网络中的单洞，同时引入环上节点动态替换方法，把环转换为网络的边界。实验验证，AIBNDA算法在网络的低节点度的情况下，能获得比较高的检测准确率;并且在网络中洞的个数比较多的情况下，算法的通信量能得到降低。

[1]Khan I M，Jabeur N，Zeadally S．Hop-based Approach for Holes and Boundary Detection in Wireless Sensor Networks[J]．IET Wirel．Sens．Syst．，2012，2(4):328－337．

[2]Simek M．Bocek J Moravek．Optimization of Boundary Recognition Algorithms for Wireless Sensor Network Applications[C]//Telecommunications and Signal Processing(TSP)，2011 34th International Conference on Digital Object Identifier，2011:189－194．

[3]郑婵，尹令，孙世新．“无线传感器网络中d-Hop 2-连通容错支配集的分布式构造算法”[J]．传感技术学报，2012，25(5):696－701．

[4]王新民，肖亚辉，顾晓婕．“基于混合优化的移动传感器网络反隐身研究”[J]．传感技术学报，2012，25(1):94－98．

[5]Simek M Bocek，Moravek J．Optimization of Boundary Recognition Algorithms for Wireless Sensor Network Applications[C]//Telecommunications and Signal Processing(TSP)，2011 34th International Conference on Digital Object Identifier，2011:189－194．

[6]Khan I M，Khan M Z，Mokhtar H Merabti．Enhancements of the Self-Detection Scheme for Boundary Recognition in Wireless Sensor Networks”[J]．Developments in E-systems Engineering(DeSE)，2011:448－453．

[7]Khan I Mokhtar，Merabti H．A New Self-detection Scheme for Sensor Network Boundary Recognition[C]//Local Computer Networks，2009．LCN 2009．IEEE 34th Conference on Year，2009:241－244．

[8]Ghrist R，Muhammad A．Coverage and Hole-detection in Sensor Networks Via Homology[C]//Proc．4th Internat．Sympos．Information Processing in Sensor Networks，2005:254－260．

[9]Olga Saukh，Robert Sauter，Matthias Gauger，et al．On Boundary Recognition without Location Information in Wireless Sensor Networks[C]//ACM Transactions on Sensor Networks，Article 20，Publication date:June，2010，6(3):20－35．

[10]Funke S，Klein C．Hole Detection or:How Much Geometry Hides in Connectivity?[C]//Proc．22nd ACM Sympos．Computational Geometry，2006:377－385．

[11]Wang Y，Gao J，Joseph Mitchell S B．Boundary Recognition in Sensor Networks by Topological Methods[C]//12th Annual Nternational Conference on Mobile Computing and Networking(MobiCom’06)，Los angeles，USA，September，2006:122－133．

[12]吴拱星，黄廷磊．基于拓扑的无线传感器网络边界节点检测[J]．桂林电子科技大学学报，2012，32(5):373－377．

[13]黄化吉，冯穗力等．NS网络模拟和协议仿真[M]．北京:人民邮电出版社，2010．