基于LS-SVM及嵌入式技术的力敏传感器温度补偿*

乔爱民，何博侠，张 炜

(1．蚌埠学院，安徽蚌埠233000;2．南京理工大学，南京210094;3．蚌埠传感器系统工程有限公司，安徽蚌埠233030)

传感器是组建自动检测与控制系统的重要环节。随着自动检测与控制技术的不断发展，对传感器的测量精度、稳定性、工作环境等提出了更高的要求。

一般情况下，力敏传感器在使用过程中被当作是线性传感器来使用，但实际上绝大多数力敏传感器的输入输出关系是非线性的关系，同时，传感器的输出还受环境温度的变化而变化，在某些要求较高的场合下，如果对非线性和温度不加以补偿修正会带来比较大的测量误差。

目前，力敏传感器的非线性和温度补偿有硬件和软件补偿方法，硬件补偿可以通过专用的弹性模量补偿片和温度补偿应变片或复合补偿丝来实现，对非线性和温度补偿有一定的作用，但是作用仍然有限。

智能仪表和计算机目前广泛应用于测控系统，采用软件对传感器的非线性及温飘进行补偿的方法得到了广泛的应用[1－4]。软件补偿方法是在测控系统中增加一个由计算机实现的软件补偿环节，用软件结合硬件补偿电路或单独采用软件对传感器进行非线性和温度补偿。目前，常用的软件补偿方法有最小二乘法，分段插值或拟合，BP神经网络等。对于分段插值拟合方法，对非线性和温度补偿有一定的作用，但补偿效果受到分段区间及插值点制约较大，有时为了追求较好的补偿效果，需要较多的分段区间和温度分布区间，造成计算量及数据存储空间较大[1]，不利于在嵌入式智能仪表上使用。最小二乘法和BP神经网络拟合是基于误差平方和最低的计算方法来求最优解的，易陷入局部最小点，有可能导致得不到全局最优解的情况[2－6]。支持向量机是由Vapnik在统计学习理论基础上建立起来的一种基于数据的机器学习方法，采用结构风险最小化原则，较好地解决了小样本、非线性、高维数及局部极小点等神经网络(artificial neural network，ANN)的先天性问题[7－11]。LS-SVM是普通SVM的一种新的拓展，把二次优化问题转化为一个线性方程组的求解问题，在具有拟合精度较高的情况下，降低了计算复杂性，从而提高了实现速度[2－6，12－13]。目前，基于SVM及模拟退火算法对传感器进行温度补偿绝大多数是在PC机上完成[1－4]，对于在嵌入式智能仪表上采用SVM及模拟退火算法等方法对传感器的温度补偿还没有相关文献提及，本文采用LS-SVM融合改进的模拟退火算法，并结合嵌入式技术，以期在应用广泛的嵌入式智能仪表上实现基于LS-SVM融合改进的SA算法对力敏传感器进行温度补偿。

1 LS-SVM基本原理

一非线性系统的输入、输出样本数据集合{xi，yi}(i=1，2，3，…，n)。其中 xi为 n 维系统的输入向量空间，yi是系统的输出向量空间，xi∈Rn，yi∈R。依据经典SVM思想，通过非线性映射φ(·)将n维输入空间映射到高维特征空间(Hilbert空间)，然后在此高维特征空间建立该非线性系统的最优线性回归函数

标准SVM以模型精度不敏感损失函数作为风险化的估计问题，因此，可建立优化目标表示为

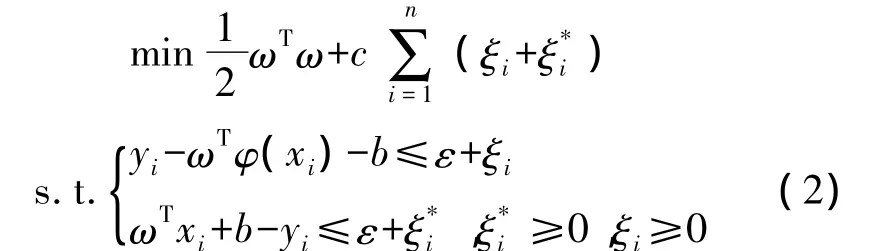
与标准的SVM不同，LS-SVM回归算法通过在优化目标中选择不同的损失函数，可用误差ξi的二范数来表示，所以优化问题最终变为

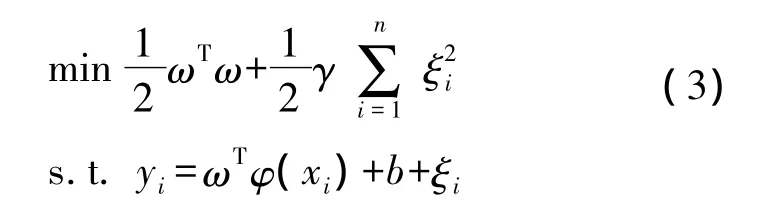
式中:ξi是非线性系统模型样本的回归误差，γ可以调节系统回归误差，其值为正实数，可综合考虑系统回归模型的复杂度和泛化能力来进行选取，一般情况下，γ值越大，模型的回归误差就越小，但同时，计算量及学习时间相应地变长。

式(3)是一个典型的条件约束优化问题，而作为线性回归系数的ω有可能维数很高甚至为无限维，直接优化可能耗时很长且有可能得不到优化结果，因此，可以通过将该条件约束优化问题转化为其对偶空间中，以实现将条件约束优化转换为无条件的无约束优化，可通过建立拉格朗日(Lagrange)方程求解。

式中ai为拉格朗日乘子。

利用库恩－塔克(KKT)最优化条件求得最佳的a和b，引入Mercer条件，该优化问题的解决则转化为求解下列的方程组:

其中 X=(1，…，1，1)T，Ψ = φ(x)Tφ(xi)为符合Mercer条件的核函数，a=(a1，a2，…，an)T，Y=(y1，y2，…，yn)T，选取径向基核函数为:

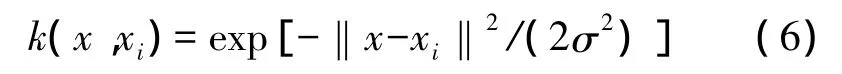
可最终得到LS-SVM的回归模型为:

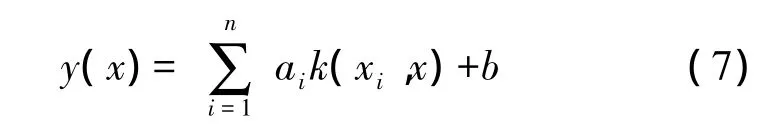
2 传感器的LS-SVM模型

2．1 传感器的输入输入输出特性

在常规使用时，一般将力敏传感器的输入输出特性近似规划为一维线性函数关系，设传感器的输出为y，输入为x，则y=kx+b，其中的b为传感器的零点输出。该函数关系在传感器实际使用时有操作简单方便的特点，而实际上，力敏传感器的输入输出关系为典型的非线性函数关系，输入量除了载荷外，还应该包含力敏传感器的使用环境温度t，即实际上的传感器输入输出关系为:y=f(x，t)。在很多环境温度变化大的场合如昼夜温度变化及四季温度的变化等场合，找出实际的传感器输入输出关系可以保证测试精度的提高。

2．2 传感器的LS-SVM模型

传感器的LS-SVM模型见图1。模型分为两个部分，一部分为训练过程，另一部分为回归过程。在训练过程中，力敏传感器的输入量为已知的标准力源输入，经过ADC转为为离散的数字量，力敏传感器的环境温度由数字温度传感器测得，数字温度传感器输出对应的离散数字量，由于训练样本为力敏传感器和温度传感器的输出的数字量，其属性值变化较大，对于16 bit的ADC，其变化范围为0～65535，而核函数受样本向量内积影响较大，对于0～65535这样大的属性值，必然会增加训练过程中的计算量及计算的复杂性。因此，在训练和回归过程中需要对两类传感器的数字输出量进行归一化处理，以减少计算复杂度和加快收敛速度。归一化后的Xdi和Xi按下式求解。

其中的β为小于等于1的正实数，在实际规划时可以根据情况给定一个确定的值，通过归一化处理后，Xdi就处于[0，1]的属性区间，并且训练机和回归机输出中则包含了载荷和温度信息。

图1 力敏传感器的LS－SVM模型

首先通过LS-SVM融合改进的模拟退火算法(SA)得到力敏传感器的非线性回归模型，然后利用该非回归模型对力敏传感器的输出作出预测输出。

2．3 全局寻优策略

在LS-SVM中，正则化参数γ和核宽度σ一般都是先根据经验选取，这增加了参数选取的盲目性，本文采用LS-SVM融合模拟退火算法(简称SA)对传感器的非线性模型进行全局寻优。SA是基于蒙特卡洛迭代求解策略的一种适用于组合优化问题的启发式搜索技术。模拟退火算法与初始值无关，是已经在理论上被证明是一种可以有效地避免落入局部最优而完全可以搜索到全局最优解的优化算法，且易于实现[4，14]，这一点非常适合于嵌入式系统上应用，但是传统的SA收敛速度慢，计算费时，这一点又不适于基于嵌入式技术的智能仪表在线补偿，因此，采用改进的模拟退火算法融合LS-SVM实现对传感器非线性模型的全局寻优。

LS-SVM融合SA算法的寻优性能主要取决于状态参数组合、新状态接收函数、温度更新函数、内外循环终止准则及初始温度等，本文中主要对参数组合和分类准确率及新状态接收函数进行了改进，以便便于在嵌入式智能仪表上应用。①参数组合初始化:运用SA时同时对LS-SVM参数(正则化参数γ和核宽度σ)和LS-SVM训练机输入变量Xdi寻优，以剔除对寻优无关的属性参数，降低代计算的复杂度，产生新的参数组合出发点应是尽可能使产生的参数遍布全部参数组合空间;②分类准确率:采用十折交叉验证法，将训练数据集分成m份(根据训练样本的大小确定)，轮流将其中m－1份作为训练数据、1份作为测试数据进行试验。m次结果正确率的平均值作为对分类准确率的估计;③新状态接收函数:在通过分类准确率估计的状态参数组合中随机抽取子集进行随机扰动，得到目标函数残差在允许范围内，允许该状态作为下一步迭代的新状态。

LS-SVM融合改进的SA寻优步骤:

步骤1:在给定的参数组合范围内随机选择初始参数组合，计算相应的LS-SVM分类准确率;

步骤2:如果当前的参数组合没达到分类准确率指标，设定Xi+1=Xi+ηελ0作为当前参数组合邻域内新状态，其中，η是一系数，用来调节随机扰动的幅度，ε为随机扰动且满足柯西分布，λ0为步长。检查Xi+1是否满足约束条件直到满足为止，计算相应的分类准确率R(Xi+1)，得到目标函数残差ΔR=R(Xi+1)－R(Xi);

步骤3:．更新状态:若ΔR＞0，则预接受新状态Xi+1;若 ΔR＜0，则按概率 P=exp(－ΔR/T)接受新状态Xi+1(T为温度);

步骤4:在温度T下，重复步骤(2)和步骤(3)，逐步降低温度T，温度T的降低策略:

a．如果 ΔR＞0，Tk+1=T0/(1+ΔN)，其中的 N 为SA中目标函数的被调用次数，T0为初始退火温度;

b．如果 ΔR＜0，Tk+1=ζTk，其中 ζ为小于 1 的正实数。

步骤五:重复步骤(2)～步骤(5)，直至符合收敛条件结束。

3 嵌入式智能仪表的软硬件设计

3．1 硬件设计

嵌入式硬件采用双核结构，具体嵌入式智能仪表的硬件结构如图2所示。

图2 硬件结构框图

信号调理主要实现对传感器信号的滤波、抗混叠等处理，数模转换(ADC)采用24 bit的集成数模转换器AD7190，温度的采集由16 bit的数字温度传感器ADT7310完成。针对LS-SVM训练机运算量较大的情况，采用高性能的最高主频可达333 MHz的超级哈弗架构(SHARC)处理器ADSP－21478来实现LS-SVM融合SA算法，运算的结果由SHARC处理器通过16 bit的数据总线和读写等控制总线传输给微控制器(MCU)MSP430F135，从而可提高数据的吞吐量。MSP430F135主要用来控制键盘显示、通信、存储等外设，同时对SHARC处理器进行读取数据、发送命令等操作，在MSP430F135上运行支持多任务的嵌入式操作系统ucOSⅡ。

通过双核硬件结构，运算量较大的LS-SVM融合改进SA算法由SHARC处理器单独完成，从而可以提高运算速度和缩短LS-SVM融合SA的训练时间。

3．2 软件设计

软件设计包含两大部分:一部分是将LS-SVM融合SA算法移植到SHARC处理器中，另一部分为MCU的控制程序。

LS-SVM融合SA的算法根据上文提到的算法步骤对C版本LS-SVMlab1．5进行改写，其中的正则化参数γ和核宽度σ由改进的SA算法进行全局寻优。MCU控制程序由嵌入式操作系统ucOSⅡ实现对多任务的调度，是否需要对力敏传感器进行温度补偿可由软件控制。具体的软件流程图见图3。

图3 软件流程图

4 试验结果分析

实验数据采用表1数据，传感器选用量程为1 000 N的拉压两用S型力敏传感器，放在可调温的温控箱和可设定的冷柜中通过给传感器施加不同的力，然后改变温控箱及可调温冷柜的温度获得对应的ADC转换值和数字温度传感器的输出数字量。得到表1中的数据，表中用Dadc表示数模转换器AD7190对应相应压力转换后的数字量，选择16 bit有效位，DT表示数字温度传感器ADT7310对应相关温度的输出数字量，选择13 bit温度数据格式。将温度为－25℃、0℃、35℃和60℃作为训练样本，将温度为20℃作为测试样本。

表1 各环境温度下传感器的标定数据

补偿前后各环境温度下传感器的线性关系如图4和图5所示。图中的纵坐标为相邻等份载荷点的差值除以1 000，根据此差值和载荷等份点的关系可以看出随着温度的变化，自身是非线性的传感器输入输出特性随环境温度的变化有较大的变化，在－20℃时，呈现较大的非线性误差，其非线性误差约为0．7%。

图4 传感器补偿前非线性

由图4可知，补偿后的传感器非线性得到较为明显的改善，在70℃时呈现较大的非线性误差，其非线性误差约为0．06%。通过非线性补偿传感器的非线性得到较大改观。

图5 传感器补偿后非线性

补偿前后各环境温度下传感器随温度漂移特性如图6和图7所示。

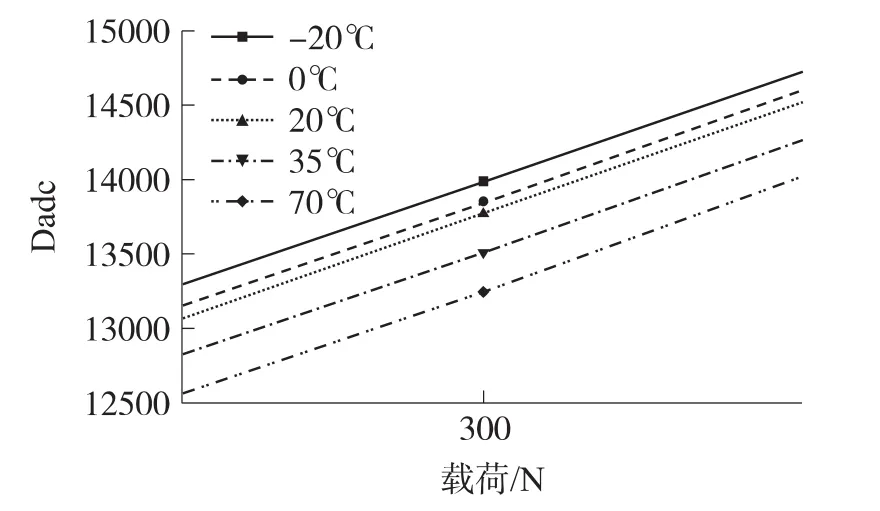
图6 传感器补偿前全温度范围内漂移

对比图5和图6中当传感器加载300 N时对应的ADC输出值Dadc可知，在补偿前，Dadc在全温度范围内的漂移量约为1 000，在补偿后，其全温度范围内Dadc的漂移量大约为50左右，通过补偿后，由温度变化带来的漂移量大为降低。

图7 传感器补偿后全温度范围内漂移

5 结论

本文结合LS-SVM支持小样本非线性系统回归精度高及改进SA算法在全局寻优中的突出优势，提出了一种LS-SVM融合改进的SA算法，构建力敏传感器的输入输出模型并应用于嵌入式智能仪表中，实现了对力敏传感器的温度及非线性在线补偿。

嵌入式智能仪表的结构采用双核模式，LS-SVM融合改进的SA算法移植于高性能的SHARC处理器中，16 bit的MCU主要完成人机交互、通信、数据存储等功能，从而保证了测量的实时性，实验结果证明，该方法的补偿精度较高，在嵌入式智能仪表上运行是切实可行的。

[1]樊尚春，张秋利，秦杰．基于样条曲线插值的压力传感器的温度补偿[J]．北京航空航天大学学报，2008，32(6):684－686．

[2]刘涛，王华．传感器非线性校正的遗传支持向量机方法[J]．电子测量与仪器学报，2011，25(1):56－60．

[3]魏国，刘剑，孙金玮，等．基于LS-SVM的非线性多功能传感器信号重构方法研究[J]．自动化学报，2008，36(8):869－875．

[4]樊晓宇，王玉宝，卢国伟，等．基于遗传模拟退火算法的压力传感器温度补偿系统[J]．传感技术学报，2008，21(9):1532－1535．

[5]黄丽，孙玉坤，嵇小辅，等．基于CPSO玉LS-SVM融合的发酵过程软测量建模[J]．仪器仪表学报，2011，32(9):2066－2070．

[6]相征，张太镒，孙建成．基于最小二乘支持向量机的非线性系统建模[J]．系统仿真学报，2006，18(9):2684－2687．

[7]Suykens J A K，Vandewalle J．Least Squares Support Vector Machine Classifiers[J]．Neural Processing Letters，1999，9(3):293－300．

[8]Suykens J A K，Vandewalle J．Nonlinear Modeling and Support Vector Machines[M]．In:Proceedings of the 18th IEEE Instrumentation and Measurement Technology Conference，2001:287－294．

[9]Vapnik V．张学工[译]．统计学习理论的本质[M]．北京:清华大学出版社，2000:126－127．

[10]Vapnik V．An Overview of Statistical Learning Theory[J]．IEEE Transaction Neural Networks，1999，10(5):988－999．

[11]蒋蔚，伊国兴，曾庆双．基于SVM数据融合的实时粒子滤波算法[J]．系统工程与电子技术，2010，32(6):1334－1338．

[12]谢建宏．基于数据依赖核LS-SVM的压电智能结构冲击损伤检测[J]．传感技术学报，2012，(6):864－868．

[13]梁秀英，李小昱．用多波长和LS-SVM补偿土壤温度的方法研究[J]．传感技术学报，2011，24(8):1228－1232．

[14]李瑾，刘金朋，王建军．采用支持向量机和模拟退火算法的中长期负荷预测方法[J]．中国电机工程学报，2011，31(16):63－66．