受限非线性最优控制问题的三角正交函数求解方法
2013-04-27李树荣
李树荣
(中国石油大学信息与控制工程学院,山东青岛266580)
在求解最优控制问题的方法中,直接法始终是一种被广泛应用的方法[1-2]。其中,利用某些函数序列对原控制问题进行近似从而进行直接求解的方法在直接法中也多有使用。Chen等[3]将沃尔什序列法引入最优控制问题的直接求解中,并得到相应最优控制问题的分段常数解。勒让德小波法[4]、切比雪夫多项式法[5]、傅里叶序列法[6]和高斯伪谱法[7]也被引入来对最优控制问题进行直接求解。不同于以上的正交函数,Anish等[8]提出了一种源于方脉冲函数(BPFs)的三角正交函数,给出了该函数的积分计算矩阵,并验证了三角正交函数在近似求解数值问题时较好的近似性能和较快的计算速度。笔者基于此三角正交函数,提出一种求解带有状态和不等式约束的非线性最优控制问题的数值求解方法。
1 三角正交函数
基于方脉冲函数,Anis等[8]提出了三角正交函数。通过拆分,在区间[0,1)中将一个方脉冲函数分解成两个三角正交函数TLi(t)和TRi(t):

其中 i=0,1,2,…,m-1,h=1/m。
三角正交函数的两个向量左三角函数TL(t)和右三角函数TR(t)为

1.1 函数近似
函数f(t)可用含有m项的三角正交函数序列展开为
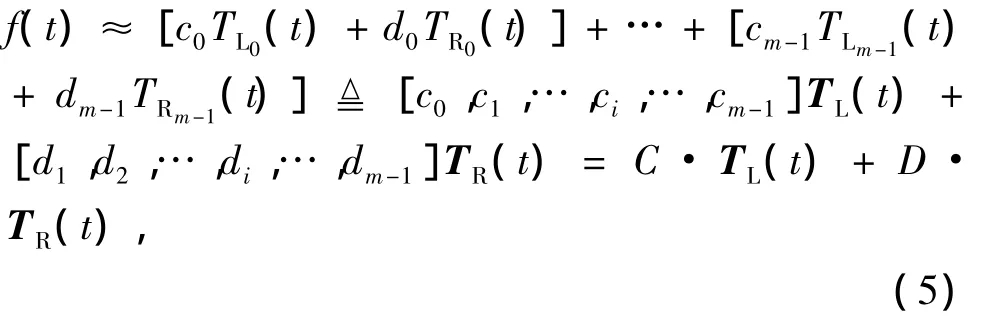
其中

1.2 积分计算矩阵
TL(t)的积分可表示为

式中,矩阵PL和PR为积分运算矩阵

其中,PL和PR为m×m维矩阵。TR(t)的积分计算与TL(t)相同。
f(t)的积分可表示为

由式(7),已知C和D便可确定f(t)的近似积分值。
2 问题描述
寻找最优向量 U(τ),和相应的状态向量X(τ),τ ∈[0,tf],使下面的性能指标最小:


其中,X(τ)和U(τ)分别为l×1维和q×1维向量。向量函数F和标量函数Si由一般的非线性函数组成并对X和U可微,tf为终端时间。并假设上述最优控制问题(8)~(10)存在唯一解。由于三角正交函数为定义在t∈[0,1]上的函数集合,引入时间转换τ=tft,将式(8)~(10)转化为
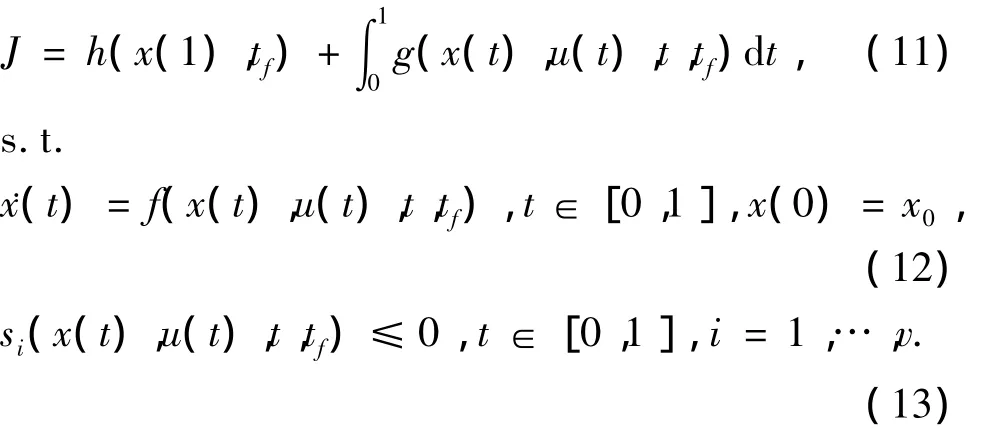
3 方法阐述
文献[9]中仅应用三角正交函数对无不等式约束的最优控制问题进行了求解,本文中对含有不等式约束的问题进行求解。
将˙x(t)和u(t)用三角正交函数序列近似为

同样,初始条件用三角正交函数展开为

将式(14)从0到t积分可得

3.1 系统状态方程近似
由式(14)和(15),系统状态方程可近似为

类似于式(14),同样可以得到

将式(14)和(17)带入式(18)中可得

引理 1[9]CL·TL(t)+CR·TR(t)=FL·
TL(t)+FR·TR(t),其中 CL,CR,FL,和 FR为 m 维系数向量,则有 CL=FL,CR=FR。
由引理1和式(20)可得

3.2 性能指标近似
由式(15)和(17)可得

与式(19)同理,可得
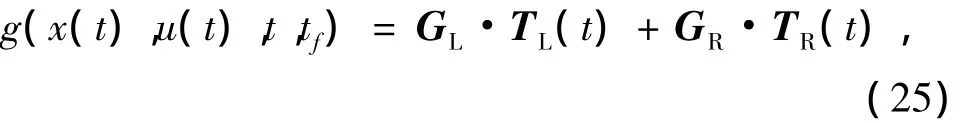
式中,GL和GR为1×m维矩阵。
将式(25)代入式(11)可得

3.3 不等式约束转化
式(13)中的不等式约束可由如下的等式约束替换[10]:
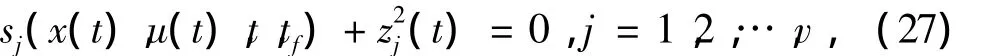
其中 zj(t),j=1,2,…,v为辅助函数。将 z(t)用三角正交函数展开可得

其中ZLj和ZRj是m维向量,同时构成v×m维矩阵ZL和ZR的第j行。同时可得
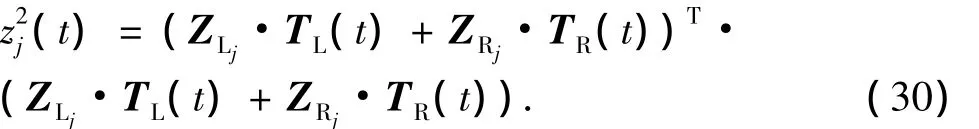
sj可改写为

定义
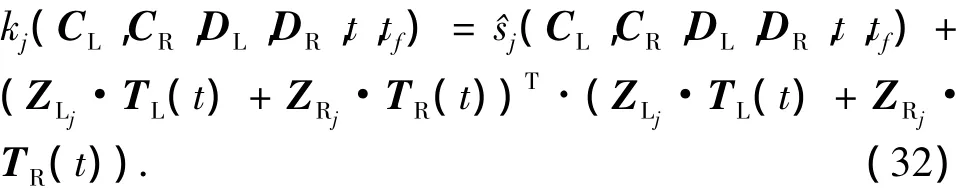
其中 j=1,2,…,v。
将式(31)可展开为

此时式(13)中的不等式约束可转化为一个通过求解 KLj,KRj,j=1,…,v 使如下函数值最小的问题:
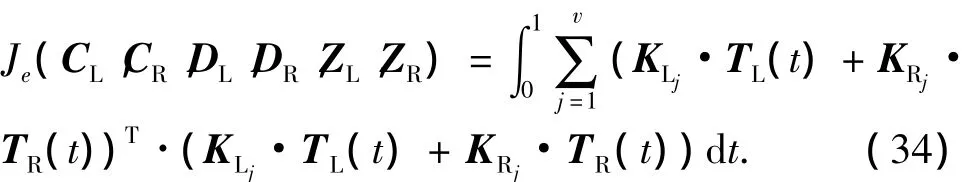
综上,原最优控制问题(11)~(13)可以转化为以下的最优控制问题。
计算 CL、CR、DL、Dr、ZL和 ZR,使下面的性能指标函数值最小:

其中λ为未知的拉格朗日乘数。为计算J*的极值,求J*的偏导数,并设其为零。

式(36)~(42)可用内点法求解。
在求得未知系数CL,CR,DL和DR的最优解后,将其代入式(15)和(17)便可得到新一轮迭代所需的x(t)和u(t)。将新得到的x(t)和u(t)代入式(11)~(13)中便可得到新一轮迭代所要求解的受限非线性最优控制问题。迭代计算重复进行直到满足终止条件为止。设定当如下的条件满足时计算终止:

算法流程如下。
步骤 1:设定 CL,CR,DL,DR,ZL和 ZR。
步骤2:时间区间由τ∈[0,tf]转换为t∈[0,1]。
步骤3:用式(15)求带有未知系数的控制变量。
步骤4:用式(17)求含有未知系数的状态变量。
步骤5:用式(19)计算系统状态方程。
步骤6:用式(26)计算性能指标。
步骤7:用式(33)计算不等式约束。
步骤8:内点法法求解最优控制问题(36)~(42)。
步骤9:将所求得的最优解代入式(15)和(17)得到新一轮迭代计算所需的x(t)和u(t)。
4 算例仿真
试验环境为Matlab,计算芯片为酷睿2(2.4 GHz),内存2 G。
4.1 例1
考虑范德波尔振荡器(Van der Pol oscillator)问题。该例曾在文献[11]中用切比雪夫法进行求解。计算满足约束的控制向量u(t)使如下性能指标最小:
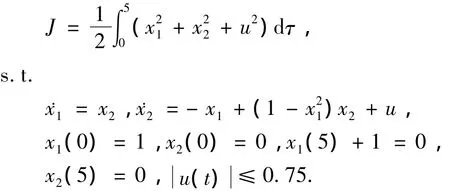
选取ε=1×10-7,用内点法进行迭代计算。表1给出了本文算法所得的性能指标和计算耗时,并与其他方法进行了比较。图1给出了状态变量的计算结果,图2为最优控制轨迹。

表1 例1仿真结果比较Table 1 Results comparison of example 1
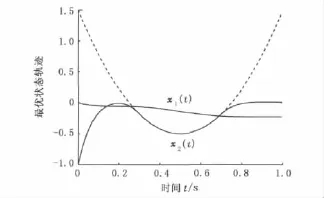
图1 例1最优状态轨迹Fig.1 Optimal states of example 1

图2 例1最优控制轨迹Fig.2 Optimal control of example 1
4.2 例2
考虑来自文献[12]的问题,计算控制向量u(t),使如下的性能指标函数值最小:
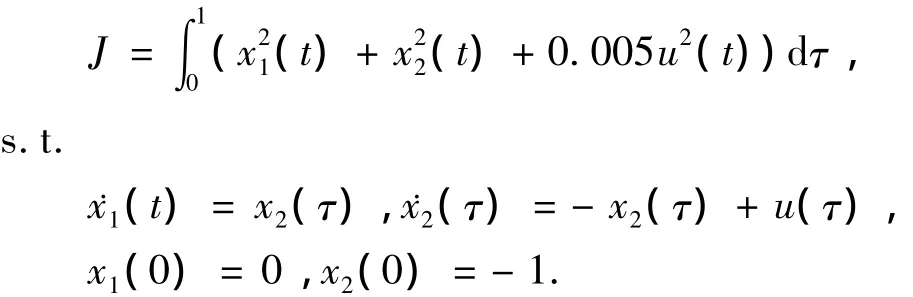
状态变量不等式约束为

选取ε=1×10-7,用内点法进行迭代计算。表2给出了本文算法所得的性能指标和计算耗时,并与其他方法进行了比较。图3给出了状态变量的计算结果,图4为最优控制轨迹。

表2 例2仿真结果比较Table 2 Results comparison of example 2

图3 例2最优状态轨迹Fig.3 Optimal states of example 2
以上两个仿真算例表明,本算法可以应用于求解受限最优控制问题。在满足题设对控制或状态限制的情况下,本算法可较切比雪夫多项式法得到更佳的性能指标,并且计算耗时更少。这样结果的出现,得益于三角正交函数简单的结构,对函数的近似性能好,这样的特性使得三角正交函数有较快的收敛速度和对函数较好的近似性。
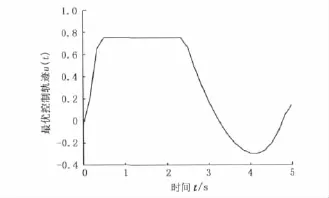
图4 例2最优控制轨迹Fig.4 Optimal control of example 2
5 结束语
针对带有终端状态约束、不等式约束的非线性最优控制问题,提出了一种基于三角正交函数的直接计算方法。该方法用系数待定的三角正交函数将控制变量和系统状态进行展开,进而将性能指标函数、状态方程和不等式约束等进行近似,从而将非线性最优控制问题转化为一系列代数方程进行求解。这样简化了求解问题的复杂性,将原非线性受限最优控制问题转化为代数方程,借助求解代数方程,实现了对原最优控制问题的直接求解。试验结果验证了该算法求解最优控制问题的有效性;该算法在满足题设限制的情况下,可得到较切比雪夫多项式算法更快的计算速度和更好的性能指标,验证了该算法在求解此类最优控制问题上有较好的收敛性和计算精度。
[1] 雷阳,李树荣,张强,等.一种求解最优控制问题的非均匀控制向量参数化方法[J].中国石油大学学报:自然科学版,2011,35(5):180-184.
LEI Yang,LI Shu-rong,ZHANG Qiang,et al.A non-uniform control vector parameterization approach for optimal control problems[J].Journal of China University of Petroleum(Edition of Natural Science),2011,35(5):180-184.
[2] 王峰,李树荣.多目标产业结构优化最优控制模型的改进及求解[J].中国石油大学学报:自然科学版,2011,35(2):182-187.
WANG Feng,LI Shu-rong.Improvement on a multi-objective optimal control model of industrial structure optimization and its solution[J].Journal of China University of Petroleum(Edition of Natural Science),2011,35(2):182-187.
[3] CHEN C F,HSIAO C H.A Walsh series direct method for solving variational problems[J].Journal of the Franklin Institute,1975,30:265-280.
[4] RAZZAGHI M,YOUSEFI S.Legendre wavelets direct method for variational problems[J].Mathematics and Computers in Simulation,2000,53:185-192.
[5] HORNG I R,CHOU J H.Shifted Chebyshev direct method for solving variational problems[J].International Journal of Systems Science,1985,16:855-861.
[6] MOHSEN R,MEHDI R,ADBOLLAH A.Solutions of convolution integral and Fredholm integral equations via double Fourier series[J].Applied Mathematics and Computation,1990,40:215-224.
[7] 李树荣,韩振宇,于光金.基于高斯伪谱的最优控制求解及其应用[J].系统科学与数学,2010,30(8):1031-1043.
LI Shu-rong,HAN Zhen-yu,YU Guang-jin.Numerical algorithm of optimal control based on a gauss pseudospectral method and its application[J].Journal of System Science and Mathematical Science Chinese Series,2010,30(8):1031-1043.
[8] ANISH D,ANINDITA D,GAUTAM S.A new set of orthogonal functions and its application to the analysis of dynamic systems[J].Journal of the Franklin Institute,2006,343:1-26.
[9] ANISH D,GAUTAM S,SUNIT K S.Block pulse functions,the most fundamental of all piecewise constant basis functions[J].International Journal of Systems Science,1994,25:351-363.
[10] MARZBAN H R,RAZZAGHI M.Hybrid functions approach for linearly constrained quadratic optimal control problems[J].Applied Mathematical Modelling,2003,27:471-485.
[11] KLEINMAN D L,FORTMANN T,ATHANS M.On the design of linear systems with piecewise-constant feedback gains[J].Automatic Control,IEEE Transactions on,1968,13:354-361.
[12] HUSSEIN J.Direct solution of nonlinear optimal control problems using quasilinearization and chebyshev polynomials[J].Journal of the Franklin Institute,2002,339:479-498.
