齿轮瞬态温度场的仿真分析
2013-04-27孙志礼王宇宁印明昂
孙志礼,王宇宁,印明昂,杨 丽,杨 强
(东北大学机械工程与自动化学院,沈阳 110189)
0 引言
齿轮传动具有传动平稳、高效,结构紧凑等优点,被广泛应用到制造、交通运输、冶金、化工、制药以及航空航天等各个领域,以高速、质载和轻质量为特征的航空齿轮传动更是占据着越来越重要的地位。航空齿轮在传动过程中会产生大量的热,并且会形成不均匀的温度场,其温度场的分布情况对齿轮系统的传动效率、动态性能以及承载能力等具有重要的影响,并且温度场对于传动系统的工作强度、动力性能、抗胶合能力、热变形等问题也都具有重要影响[1]。国内外很多学者对齿轮温度场的进行了理论、实验研究和仿真分析。刘志全等[2]采用热网络法分别研究了军用直升机齿轮传动系统的瞬态温度场的分布规律。Wang K L和Cheng H S[3]研究了齿轮啮合瞬时的闪现温度,分析了齿轮闪现温度和本体温度的分布情况,并研究了齿宽、分度圆以及齿顶尺寸等对齿轮温度场分布的影响。吕品[4]等研究了温度分布对自由盘层流换热的影响。杨志民[5]等采用双向测量方法对航空发动机燃烧室出口温度场进行了分析和研究。
本文以直齿圆柱齿轮为研究对象,运用有限元方法和传热学理论建立直齿圆柱齿轮模型,研究分析不同周期温度场随时间的变化以及啮合点温度的变化。对于指导齿轮可靠性设计和热应力与热变形等计算提供了重要依据。
1 齿轮瞬态温度场的微分方程和定解条件
有限元方法与热网络法相比,在温度场求解过程中具有较高的计算精度,在进行齿轮瞬态温度场的有限元仿真时,采用精度更高、速度更快的热分析实体单元Solid70,加载时将齿轮摩擦产生的热量当做移动热源,用此热源沿啮合面的移动来模拟齿轮啮合的过程。
传热学以能量守恒定律和傅里叶定律为基础,主要研究由温度差引起的热量传递过程和由物质组成质量分数差引起的物质迁移现象,对啮合齿轮进行热分析应建立数学模型和定解条件。本研究根据傅里叶定律和能量守恒定律来建立物体中各点温度应该满足的关系变化式就是导热微分方程[6],即

式中:λ为齿轮材料各方向的导热系数;Φ˙为物体中的内热源;ρ为微元体的密度;c为微元体的比热。
对齿轮来说,把啮合面摩擦的热流量作为边界条件施加于外表面,所以齿轮瞬态温度场的导热微分方程中不包含热源项。另外,齿轮材料各方向的导热系数相同,其导热微分方程为
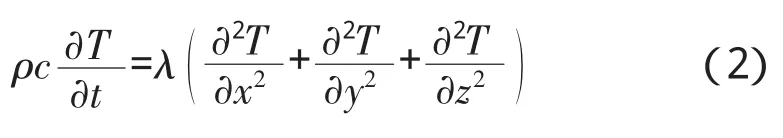
对于瞬态导热,定解条件包括2方面:给出初始时刻的温度场分布,即初始条件;给出导热物体边界的温度或换热情况条件,即边界条件。初始时刻的温度分布,可以是均匀的,也可以是非均匀的。
初始条件可以表示为

2 齿轮各界面边界条件分析
正确计算齿轮各界面的边界条件是齿轮瞬态温度场分析结果的前提,求解直齿圆柱齿轮瞬态温度场,除了要满足式(2)外,还要确定各表面的边界条件,如图1所示[7]。
(1)齿面啮合区(m区)

图1 齿轮单齿计算区域
齿面啮合区既有摩擦热流量的输入,又有对流换热边界条件,同时符合第2、3类边界条件,所以其边界条件为

(2)齿顶面、齿根面及啮合面非工作区(t区)
齿轮齿顶面、齿根面及啮合面非工作区只有对流换热边界条件,属于第3类边界条件
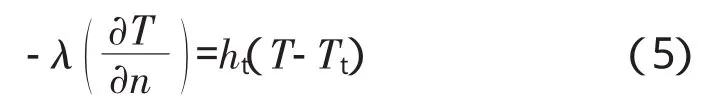
(3)齿轮端面(s区)
齿轮端面和齿顶面一样边界条件为对流换热
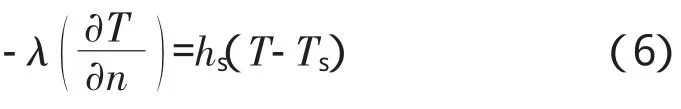
(4)齿轮底面(d区)
齿轮底面因为离啮合面较远,温度梯度变化小,可以假设为绝热表面,其边界条件为

(5)齿轮分齿截面(f区)
齿轮分齿截面符合导热边界条件,其边界条件为
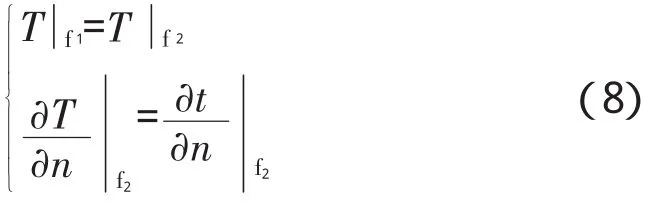
啮合接触区的摩擦生热主要与接触区的压力、摩擦系数和相对滑动速度有关。本文采用计算接触区单位面积的瞬时摩擦热流量,即热流密度q

由于所分析的航空传动齿轮圆周速度较高,所以采用啮出侧喷油润滑方式冷却,将润滑油直接喷到啮合面的节点位置,以较多量的润滑油带走较大的热量,啮合面对流换热系数hm的计算公式为

式中:ω为齿轮的旋转角度速度;ko为润滑油的热传导率;ρo为润滑油的密度;co为润滑油的比热容;δo=ko/ρoco为润滑油的导温系数;vo1为润滑油的运动黏度;rc为齿轮分度圆半径;H为轮齿的高度;qtot为标准化冷却量。
3 直齿圆柱齿轮的瞬态温度场的有限元分析
齿轮传动系统连续稳定工作一段时间达到热平衡状态,本体温度场不再随时间变化,但是齿轮传动系统从开始启动到温度场达到平衡这段时间,其温度场是随时间变化的瞬态温度场。
在进行齿轮瞬态温度场计算之前,根据Blok H理论做如下假设[8]:
油价越来越贵怎么办?湖北黄梅县一辆轿车停在应急车道上。司机称,自己车子没油了,上网查了后发现可以加水当油,便加了1升水,结果发现车不能开,又叫拖车拖到加油站加了9升油,结果车子在高速上抛锚了!
(1)在轮齿的啮合过程中,摩擦热量只传给相互啮合的轮齿,热量没有向周围的流体扩散。
(2)啮合区发热量的分布和压力分布一样,呈抛物线规律。
(3)和齿轮温度场发生变化的时间相比,齿轮旋转1周所需时间较短。对每个齿来说,在齿轮啮合过程所经历的过程完全相同,所有只选取1个轮齿分析。
(4)齿轮在转动1周的过程中,每个轮齿输入的热量相同。
3.1 直齿圆柱齿轮有限元模型的建立
以直齿圆柱齿轮主动轮为例,如图2所示。齿轮的材料热物理属性见表1,齿轮的主要几何参数见表2,齿轮的扭矩为175 N·m,转速为9280 r/min。
ANSYS热分析涉及的单元大约有40余种,3维实体单元有SOLID87、SOLID70和 SOLID90。所采用的单元是热分析实体单元Solid70,如图3所示。此单元是8节点六面体单元,可以退化为棱柱单元、四面体单元和金字塔单元。和SOLID87单元相比有更高的精度,和SOLID90单元相比有更快的速度。

图2 齿轮实体模型

表1 齿轮材料的属性

表2 齿轮的基本参数
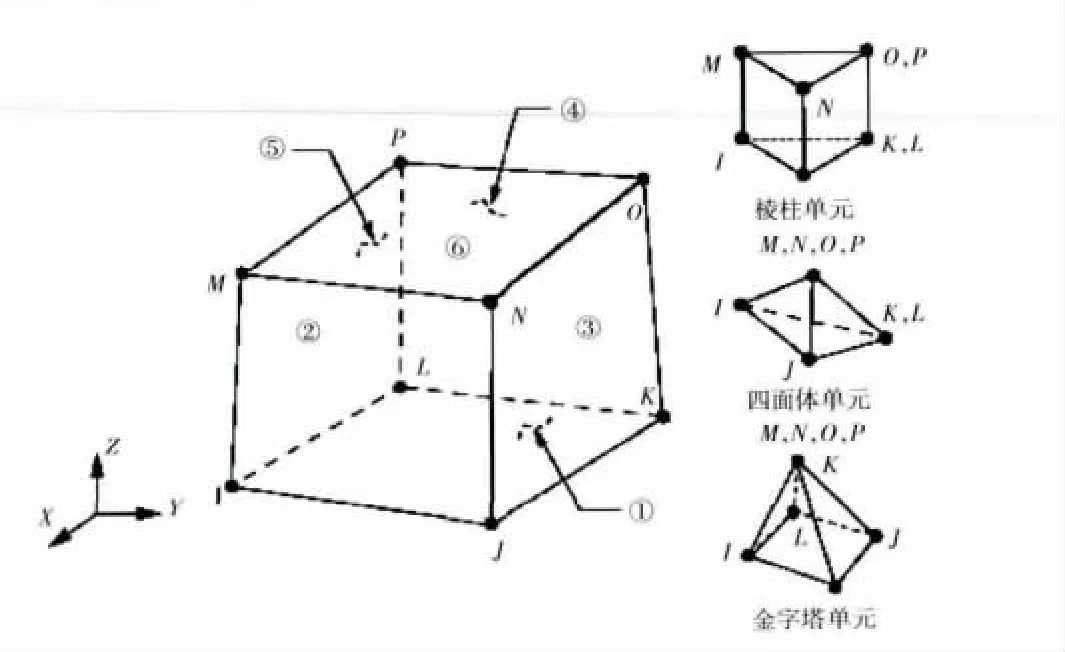
图3 SOLID70单元结构
设置弹性模量、比热、导热系数和密度等材料属性,然后运用扫略的方式进行网格划分,生成规则的六面体网格。根据已做的假设,采用单齿模型进行分析,实体模型和有限元模型分别如图4、5所示。
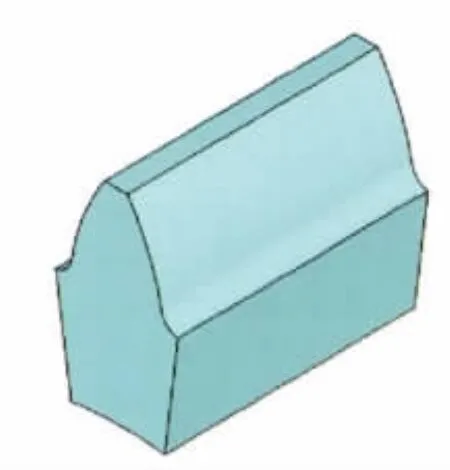
图4 单齿实体模型

图5 单齿有限元模型
3.2 边界条件的加载
热源通过啮合面某节点组的时间,即热源作用于这一节点组的时间。在啮合面尺高方向上设定n组节点(图5),热源从下到上分别依次通过到这些节点组,并且依次加载,热源的每次加载都进行1次求解,用第k次求解的齿轮温度场Tk作为第k+1次求解时的初始条件,进行第k+1次求解,然后通过递推依次向后求解。
热源在啮合面上的速度如图6所示,图中横坐标表示热源在啮合面上的位置,即啮合点所对应的半径,纵坐标表示移动的速度。

图6 热源移动速度
由边界条件的计算公式可知,啮合面的对流换热系数和润滑油的温度有关,齿轮端面、齿顶面、齿根面和非啮合齿面的对流换热系数与润滑油和空气混合物的温度有关,在齿轮开始工作到温度场达到平衡的过程中,二者的温度随时间发生变化[9]。润滑油和油气混合物的温度随时间的变化规律应该由试验测定,在没有试验数据的情况下,为了得到简化,以接近平衡状态时的温度场为初始条件,此时的润滑油温度、油气混合物的温度和稳态温度场时的温度很接近,可以认为他们相等。在施加完热流密度、对流换热系数等边界条件后,进行循环求解。
3.3 直齿圆柱齿轮瞬态热分析结果
进入通用后处理器(POST1),查看不同啮合周期的温度场,并显示温度场。然后进入时间历程后处理器(POST26),定义齿面1节点的温度为变量,显示节点温度的变化曲线。不同啮合周期温度场和节点温度变化曲线如图7所示。

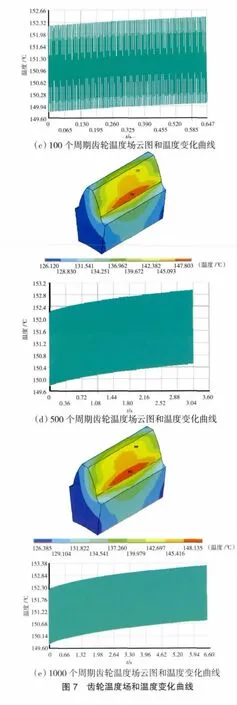
从图7可见,不同周期齿轮温度场和节点温度变化具有如下特点:
(1)不同周期齿轮温度场的分布基本不变,只是温度随着啮合周期的增多而升高。
(2)可将1个旋转周期分为啮合阶段和非啮合阶段。在啮合阶段节点温度有一个急剧升高,在退出啮合后进入非啮合阶段,温度逐渐降低。
(3)齿面温度升高后与流体的温差加大,散失的热量相应增多,在非啮合阶段,温度的下降相应增大,但由于啮合阶段温升仍然大于非啮合阶段温度的下降,所以该节点温度总体趋势还是升高。
以齿轮本体温度场为初始条件得到的该节点温度变化如图8所示,可以认为温度变化曲线是齿轮达到平衡状态后的温度变化曲线。

图8 平衡状态时温度变化曲线
4 结论
(1)移动热源法进行齿轮的瞬态温度场分析是准确可行的。
(2)随着啮合周期的增加,啮合阶段温升仍然大于非啮合阶段温度的下降,齿面节点的温度相应增高,但温度曲线的变化越来越平缓。
(3)当到达一定的周期后,啮合阶段的温升和非啮合阶段温度下降相等,此时齿轮的温度场达到平衡状态。
(4)瞬态温度场仿真对齿轮的寿命和生存能力预测具有重要意义,有必要在齿轮乏油和无油润滑状态下进一步深入研究。
[1]张永红,苏华,刘志全,等.行星齿轮传动系统的稳态热分析[J].航空学报,2000,21(5):431-433.
ZHANG Yonghong,SU Hua,LIU Zhiquan,etal.Steady state thermal analysis of planetary transmission systems[J].Acta Aeronautica et Astronautica Sinica,2000,21(5):431-433.
[2]刘志全,沈允文,陈国定,等.某直升机齿轮传动系统的瞬态热分析[J].航空动力学报,1999,14(3):309-312.
LIU Zhiquan, SHEN Yunwen, CHEN Guoding, et al.Transient thermal analysis of a helicopter gear transmission system[J].Journal of Aerospace Power,1999,14(3):309-312.
[3]WANG K L,CHENG H S.A numerical solution to the dynamic load,film thickness and surface temperature in spur gearing[J].Journal of Mechanical Design,1981,103(1):177-188.
[4]吕品,王成明,赵煕,等.温度分布对自由盘层流换热的影响[J].航空发动机,2010,36(4):8-11.
LYU Pin,WANG Chenming,ZHAO Xi,et al.Effect of temperature distribution on laminar heat transfer for free disk[J].Aeroengine,2010,36(4):8-11,
[5]杨志民,孙永飞,赵煜,等.航空发动机燃烧室出口温度场双向测量方法[J].航空发动机,2010,36(1):42-44.
YANG Zhimin,SUN Yongfei,ZHAO Yu,et al.Bi-directional measurementmethod of combustor outlet temperature field for aeroengine[J].Aeroengine,2010,36(1):42-44,
[6]杨世铭,陶文铨.传热学[M].北京:高等教育出版社,2006,1-28.
YANG Shiming,TAOWenquan.Heat transfer[M].Beijing:Higher Education Press,2006:1-28.
[7]史妍妍.基于热分析的附件机匣若干可靠性问题研究[D].沈阳:东北大学,2009.
SHI Yanyan.Study on accessory gearbox reliability based on thermalanalysis[D].Shenyang:Northeastern University,2009.
[8]Patir N,CHENG H S.Prediction of the bulk temperature in spur gears based on finite element temperature analysis[J].LE Trans,1979,22(1):25-36.
[9]王娟,王隽,姚世卫,等.减速器输出人字齿轮温度场分析[J].机械设计与制造,2008,(5):38-40.
WANG Juan,WANG Jun,YAO Shiwei,etal.Analysis of the temperature field to the sub lambdoidal gear of the retarder[J].Mechanical Design and Manufacturing,2008,(5):38-40.
[10]姚昌荣,李亚东.大跨度桥梁健康监测过程中的温度影响研究[J].华东交通大学学报,2008,25(2):5-28.
YAO Changdong,LI Yadong.Research on temperature influences in long-span bridges health monitoring[J].Journal of East China Jiaotong University,2008,25(2):25-28.
