一种利用矩阵特征值的抗干扰算法

王 春

(西安电子科技大学 电子工程学院，陕西 西安710071)

第三代移动通信，CDMA，UMTS等制式的扩频信号在实际应用中，经常受到如GSM、对讲机等信号的干扰，导致灵敏度降低或者接收不到信号，导致通话质量降低。因此抗干扰技术在实际应用中尤显重要，是业界学者的研究热点。利用FFT进行陷波的抗干扰算法，首先利用快速傅里叶变换把带有窄带干扰的时域信号，用快速傅里叶变换到频域;再根据窄带干扰信号的特点，做一个窄带平滑滤波器对干扰信号进行检测，并将检测到的干扰信号一并提取出来，同时记录干扰的位置，用提取的干扰信号与原信号在同一位置进行对消，完成频域内干扰信号的消除;最后再把去除干扰的信号进行逆傅里叶变换，得到所需的时域信号。但利用FFT进行陷波的抗干扰算法由于FFT运算量大，需要存储的空间大，导致系统的功耗增大，成本上升。基于白化噪声的抗干扰算法，首先利用白化自适应滤波器，对信号进行白化处理;然后对白化后的信号再进行相关运算，从而提高系统的抗干扰能力。输入信号具有如图1(a)所示的频谱，则白化自适应滤波器使系统所具有的频谱为图1(b)所示的形式。这样滤波器输出的频谱才是一个平坦的白色过程，如图1(c)所示。基于白化噪声的抗干扰算法，是基于对窄带干扰用白化滤波器滤波的思想来消除干扰，虽然简单，但与基于FFT的陷波算法相比，消除干扰的性能不是很理想。在实际应用中，除了算法本身的抗干扰性能，算法的实现性价比也较重要，在工程应用中，成本是需要考虑的一个重要方面。因此，找到一种既能满足性能要求，又成本低廉的实现方案成为一个亟待解决的问题。基于此，文中提出了一种利用矩阵特值进行抗干扰的算法，可以有效消除阻塞性与类单音的各种干扰，与常见的利用FFT进行陷波的算法处理相比，利用矩阵特征值进行抗干扰处理，具有计算量小、逻辑实现简单的优点，降低了抗干扰算法的复杂度。该算法从性能与资源上取得较好的平衡。

1 矩阵特征值算法介绍

在信号处理中，矩阵发挥着重要作用，矩阵的各个特征与分量都体现了信号的某个特征，只要对这些特征进行分析，就可得到各种信号处理的算法。

对信号的协方差矩阵进行特征值分解，可以得到特征值和特征向量，而信号子空间和噪声子空间就是由这些特征向量张成的［1］，大的特征值对应的特征向量就张成信号子空间，同样噪声子空间也知道了［2］。在有干扰的系统中，可以认为这些大的干扰就是信号，而信号就是噪声。那么从相关阵的特征值看，那些大的特征值张成信号空间，其余小的张成噪声空间。

观测信号为n维的向量X，X受到一个强度比较大得窄带单音信号的干扰。那么根据常见的信号分析，这个信号向量形成的相关矩阵［3］通过特征值分析信号和噪声如下

S矩阵为对应的特征值矩阵。S=diag(α1，α2，α3，…，αn)，这些特征值可以反映信号和噪声能量集中的情况。如果将α1，…，αi，…，αr按照递减的顺序排列即，α1≥α2≥…≥αi≥…≥αr≥0，那么，前i个较大的特征值将主要反映单音干扰，较为平均且较小的特征值将主要反映信号［4］。大特征值与小特征值有多个数量级的差异。通过设定一个合适的门限，就可以区分那些对应特征值对应噪声，那些特征值对应信号。

根据式(1)～式(3)得到

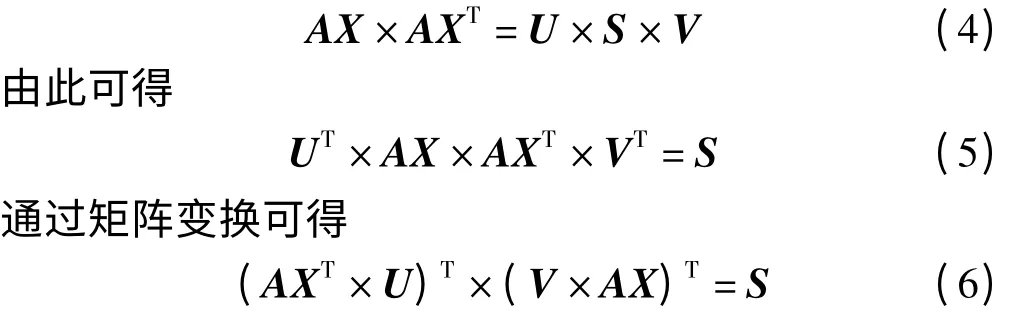
式(6)通过U，V，AX等恰好组成滤波器的关系［5］，每个滤波器产生结果的平方对应相应的特征值。那么去掉干扰的思路就可得出。通过式(6)可以得到干扰分量的滤波器系数，那么观测信号向量X进行滤波分离干扰信号和有用信号［6］，去除干扰的实现框图如图2所示。

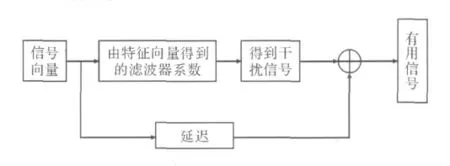
图2 干扰算法实现框图

通过对基本原理的阐述，抗干扰算法在FPGA里易于实现，系数可以在CPU或DSP中计算。

2 仿真结果

通过建立一个单音+信号模拟系统，单音代表干扰，信号代表噪声。仿真所涉及的干扰信号的强度比信号强度约高37 dB，信号的长度为8 192。检测门限5 dB。如图3所示，类似干扰会严重影响信号解调的灵敏度，有些信号甚至无法解出。干扰信号用单音信号实线表示，有用信号用白噪声信号虚线表示。

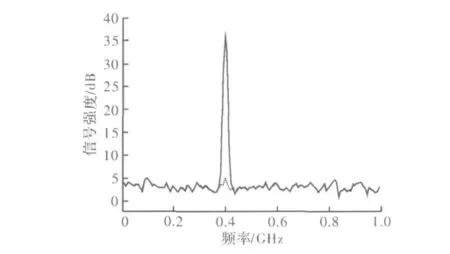
图3 信号干扰信号与有用信号功率对比图

黑色的信号是有用信号加单音干扰。灰色的信号是用上述方法去除单音干扰后的信号。那么图3就是真实的有用信号和去除干扰的有用信号的比较。

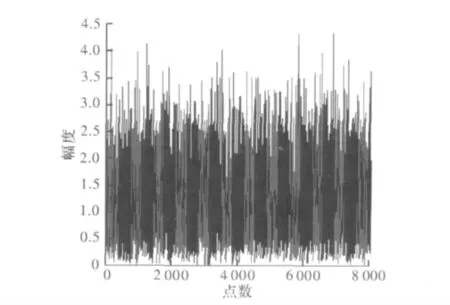
图4 原始无干扰信号与去掉干扰后的信号重合效果图

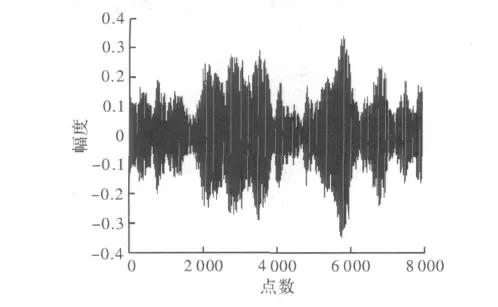
图5 误差逼近效果

图5中灰色是误差图，横坐标是点数8 192。纵坐标是信号误差的幅度。相当于分离出来的有用信号减去真实的有用信号。最大误差约为0.3。结果说明去掉干扰是成功的。对比3种抗干扰算法，所有算法的实现基于Xilinx的Virtex5器件的比较。

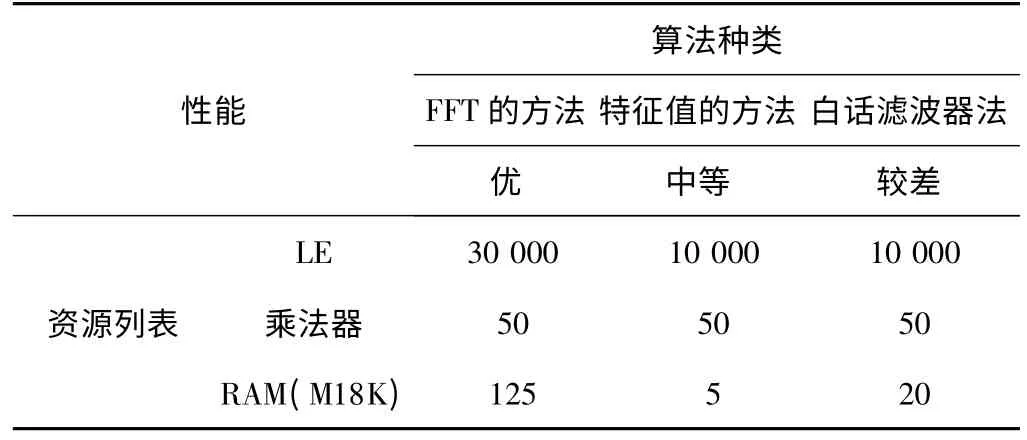
表1 3种干扰算法性能及资源比较

从表1可见，如果取折中，实现最佳性价比，特征值的方法性价比较高。

3 结束语

介绍了抗干扰算法是基于特征值所张成的信号空间来描述各个投影方向的信号特点［7］。特征值的求解，有多种解法，不同的解法，对算法的性能有影响，同时要注意相关矩阵的稳定性。以及算法实现的代价及所占用的资源。

［1］ 胡广书.数字信号处理［M］.2版.北京:清华大学出版社，2008.

［2］WEI S，MOENESS G A.Maximum signal－to－noise ratio GPS anti－jam receiver with subpace tracking［M］.USA Villanova:Center for Advanced Communications，Villanova University，2010.

［3］CORMAC D F.OFDM narrowband interference estimation using cylic prefix based algorithm［D］.Dublin Ireland:University Colledge Dublin，2006.

［4］ZHANG Dan，FAN Ping，CAO Zhigang.Receiver window design for narrowband interference suppression in ieee 802.11a system［D］.Beijing:Tsinghua Uniersity，2004.

［5］GOMAA A.A compressive sensing approach to NBI cancellation in mobile OFDM systems［C］.Global Telecommunications Conference 2010 IEEE，2010.

［6］MAHATA K.Spectrum estimation，notch filters，and MUSIC signal processing［C］.IEEE Transactions on Communication，2005(10):931－937.

［7］ 张贤达.通信信号处理［M］.2版.北京:国防工业出版社，2005.