基于Multisim10和Matlab7.0的正弦稳态电路分析

王翰卓，陈海花

(中国海洋大学 信息科学与工程学院，山东 青岛266100)

Multisim是一款专门用于电子线路仿真和设计的EDA工具软件，其提供了一个虚拟的电子实验工作台，以其界面友好、功能强大和易用性受到电子类专业人员的青睐。Matlab是一款商业数学软件，Matlab编程语言简单易用，软件具有强大的数据处理能力，可用于算法开发、数据可视化、数据分析以及数值计算等［1］。

电子类课程教学过程中，由于教学资源的限制，并不能实际演示电路实验，此时使用Multisim可以仿真实验过程，用Matlab可以精确地完成电路计算。实际上，使用Multisim可以得到直观的电路图形界面并体现实验的操作方法，但往往不能全面显示计算结果，也无法体现分析方法;Matlab则以数值计算、图形绘制见长，其编程过程反映了分析方法，但无法体现直观的电路图形。文中将两款软件综合使用，以仿真分析正弦稳态电路为例，将二者优势结合，全面反映电路的分析和实验过程［2］。

1 正弦稳态电路及其分析方法

在正弦激励的动态电路中，若各电压、电流均为与激励同频率的正弦波，则该电路即为正弦稳态电路。正弦稳态分析主要包括求解其稳态响应，计算功率以及最大功率传输定理等。分析正弦稳态电路，往往采用相量分析的方法，画出电路图的等效相量模型，然后按照分析直流纯电阻电路的方法进行分析计算，得到复数域下的节点电压和支路电流，再将其转化为时域下的结果［3］。

如图1中的RLC串联正弦稳态电路，现将电路的各个参数化为相量形式，电源有效值;电阻ZR=R;电感ZL=jωL;电容。若要求解电路总功率，应先求出电路总的阻抗，其表达式为，电路的功率因数λ=cosα，当λ=1时，电路体现纯电阻特性。电路的视在功率，其中。然后可得电路的有功功率P=S cosα，无功功率Q=S sinα［4］。

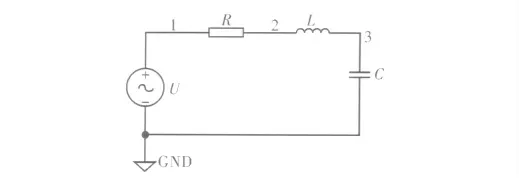
图1 RLC串联电路模型

针对于电路负载的功率，当负载电阻及电抗均可独立变化时，根据最大功率传递定律，当负载的阻抗ZL与电路的输出阻抗ZO满足共轭匹配时，负载所得到的功率最大。由此可见，当电路较为复杂时，上述过程的手工计算量较大。使用仿真软件可以实时、动态地得到实验数据和计算结果。

2 正弦稳态电路的仿真与分析

下面以一道具体的正弦稳态电路分析问题为例，阐释Multisim仿真和Matlab仿真在电路分析上的长处和不足，并引出综合使用的方法［5］。

RLC正弦稳态电路如图2所示，其中V1为电压源;峰值141 V;频率100 Hz初相为0;电感L1值为15.90 mH;R1大小为5Ω，可变电阻R2(变化范围0～10Ω);C1为可变电感，变化范围0～318.60μF。

(1)当R2=4Ω，C1=191.60μF时，R2两端电压、C1两端电压、电源电压三者的幅值和相位关系，求解此时电源提供的复功率和功率因数。

(2)R2=4Ω，则C1为何值时，电路的功率因数最大。

(3)当电阻R2和C1的参数都任意变化时，研究负载的功率变化并求负载的最大功率。

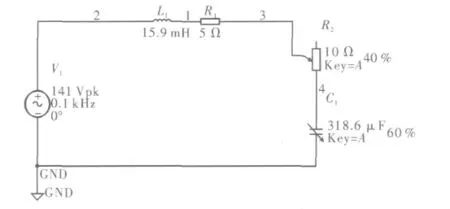
图2 正弦稳态电路

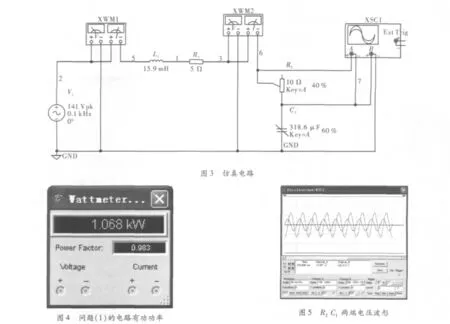
(1)基于Multisim10的仿真分析。在Multisim的Workspace中搭建图3所示的电路，为解决问题(1)，调整R2和C1的接入值，使R2=4Ω，C1=191.60μF。其中瓦特表XWM1用来显示电源输出的有功功率及功率因数，瓦特表XWM2用来显示负载的有功功率及功率因数，示波器XSC1用来显示负载R2和C1两端电压波形。

如图4所示，瓦特表XWM1显示值为问题(1)中电源提供的有功功率和功率因数，图5为此时R2和C1两端的电压波形。可以读出此时电路有功功率约为1.07 kW，功率因数约为0.98。示波器可以大致读出R2和C1两端电压的峰值，但不能得到精确的相位差。

调整C1接入电路的电容值，观察瓦特表XWM1的变化，得到功率因数为1时如图6所示，此时电容接入恰为50%，即159.30μF。

图6 问题(2)XWM1

调整R2接入电路的阻值和C1接入电路的电容，观察瓦特表XWM2的示数到最大，电容C1和电阻R2值，此时C1和R2各接入50%。C1=159.30μF，R2=5Ω。XWM2的示数如图7所示。

可见Multisim为用户提供了交互式的仿真环境，但不能得到R2和C1端电压的波形函数，以及电压相位差;在调节R2和C1的过程中，其接入值也并非连续变化，而是以每次最小变化的离散值进行调整的，在解决(2)、(3)问题时，找R2、C1参数的过程繁琐，而且不能确定最终的接入值是精确的。使用Matlab进行编程，可以克服这些问题。

(2)基于Matlab7.0的仿真分析。根据正弦稳态电路的分析方法设计算法，编写Matlab程序代码，计算并显示结果。先将电路给出的各个参数表示成复数域下的形势，对于问题(1)，求解出R2和C1上的电压相量后，用abs函数和angle函数分别显示出电源电压、R2和C1上电压的幅值和初相角，并调用compass函数绘制出这3个电压量的极坐标图;问题(2)则应用电路功率因数为1时，电路呈现纯电阻电路的特点，解出C1的值;对于问题(3)，不直接采用最大功率传输定律的方法，而是运用数学解析方法，将负载的功率P表示成C1和R2的函数，调用Matlab的diff函数和solve函数，求解方程组

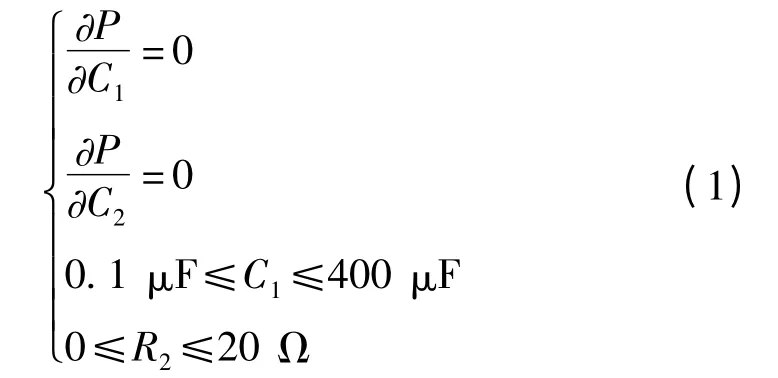
找到P的极大值以及此时对应的C1和R2，解析法的求解结果可与应用最大功率传输定律所得结果进行比对，验证该定律的正确性。为直观看出C1和R2变化时功率P的变化情况，将C1和R2用向量矩阵表示出其变化范围、精度后，调用mesh函数，绘制出以C1和R2为自变量时因变量P的三维图像。

程序运行后，显示了所求结果的精确值。对于问题(1)，根据UR2和UC1的幅值、相位的具体值可以得到其具体的波形函数UR2=61.60cos(200πt/s－0.06π)，UC1=127.92cos(200πt/s－0.56π)，UR2超前UC1π/2，图8给出了Us、UR2、UC1在极坐标系下的幅值相位关系图。此时的电路功率因数λ≈0.98，有功功率P=1.07×103W，无功功率Q=199.63 W;问题(2)可得到电路功率因数λ=1时，C1=159.31μF;图10为R2和C1参数改变时，负载功率P变化的三维图像，峰值处对应图对应P最大时的C1和R2的参数，此时C1=159.31μF，R2=5Ω。带入后验证ZC1+ZL1=0，R2=R1成立。解析结果证明了最大功率传递定理。

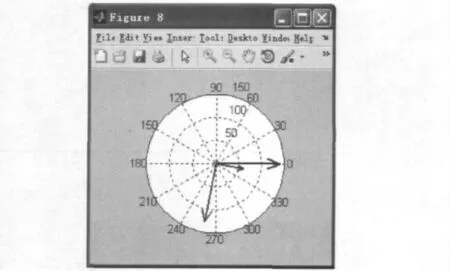
图8 Us、UR2、UC1极坐标图

Matlab的编程过程良好地体现了解题思路，其数据、图像处理能力使得大量的数据能够整体地、直观地体现出来。但此过程如果脱离Multisim的仿真，不看电路操作，只去看编程代码和计算结果，理解起来会晦涩生硬。将两种仿真结合起来，取长补短，方可得到最佳的仿真效果。

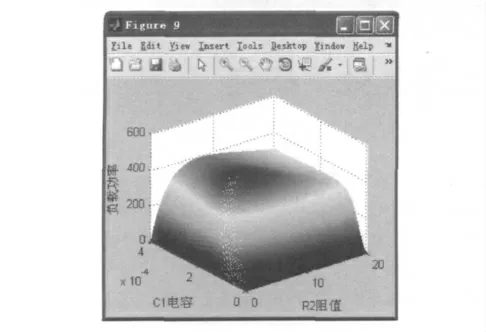
图9 P随C1和R2变化的三维图象

(3)结合式仿真。将Multisim和Matlab的仿真结合，从过程上看，Multisim体现了电路搭建和实验操作过程，Matlab体现了算法分析过程，将虚拟的实践和理论计算结合起来;从结果上看，针对问题(1)，Multisim得到了UR2和UC1的波形图如图5所示，相应的Matlab仿真得到了UR2和UC1的波函数和相位如图8所示实现了数与形的结合，针对问题(3)，Matlab得到的C1和R2的结果如图9所示，又可以为Multisim的仿真操作提供指导，避免了操作的盲目性。

3 结束语

提出一种Multisim和Matlab软件相结合的方式进行电路仿真，弥补了各自的不足，使仿真效果达到最佳。所提供的仿真方法也不失为一种解决问题的有效途径，判断电路故障、评估产品效果宜偏重于Multisim仿真;要求得到精确的电路参数、需要处理大量的电路计算时宜偏重于Matlab仿真，使用者可根据实际的情况和软件的特点灵活地选择使用。

［1］ 聂典.Multisim 10计算机仿真在电子电路设计中的应用［M］.北京:电子工业出版社，2009.

［2］ 陈怀琛，吴大正，高西全.Matlab及其在电子信息课程中的应用［M］.北京:电子工业出版社，2006.

［3］ 李瀚荪.电路分析基础［M］.北京:高等教育出版社，1983.

［4］ 王连英.Multisim和Matlab联合仿真在《自控原理》课程教学中的运用［J］.科技教育创新，2006(8):267－269.

［5］ 蒋跃文.仿真软件在探索研究型教学模式中的应用［J］.科技信息:学术版，2007(18):111－114.