一种基于Biharmonic样条插值的流形学习算法*
2013-04-24顾艳春马争鸣梁宇滔
顾艳春,马争鸣,梁宇滔
(1. 佛山科学技术学院电子与信息工程学院, 广东 佛山 528000; 2.中山大学信息科学与技术学院, 广东 广州 510220)
流形学习是一种有效的非线性降维方法。近年来,流形学习方法在数据挖掘、机器学习、图像处理和计算机视觉等多个研究领域吸引了广泛的关注。典型的流形学习方法有Isometric Feature Mapping (ISOMap)[1]、Locally Linear Embedding (LLE)[2]、Hessian Eigenmaps (HLLE)[3]、Local Tangent Space Alignment (LTSA)[4]、Laplacian Eigenmaps (LE)[5]等。这些算法具有一个共同的特征:找出每个数据点周围的局部性质,并将这些局部性质信息映射到一个低维空间中。显然,局部几何结构信息的保持和恢复程度决定了流形学习算法的优劣。在获取流形的局部信息时,流形学习算法假定流形在一个很小的范围内,局部同胚于一个欧式空间的一个连通开集,这就决定了流形学习算法在选择邻域时,要尽可能保证邻域内的点满足局部同胚条件。而当样本点较为稀疏时,邻域内的样本点很难保持局部同胚条件,从而导致上述流形学习算法在处理稀疏数据集时会造成较大的误差,甚至失效。
针对流形学习算法无法有效处理样本点稀疏的问题,目前主要有三种解决方法。一类是根据样本点的稀疏程度,自适应的改变邻域大小,从而尽可能的使邻域内的样本点满足同胚条件[6-8]。在样本点比较稀疏时,此种方法会使得邻域相对较小,这很容易造成在将局部坐标信息排列成全局坐标时由于交叠不够而使算法效果难以令人满意的现象。第二种方法是改变邻域内的局部信息选取方式,例如,Wu等[9]求取邻域时,首先对样本点集做预处理,去除样本集中的“短路”边,然后利用最短路径算法迭代出样本点间的测地线距离来选取邻域;Song等[10]通过最小化邻域内样本点间的梯度值来实现高维数据的局部线性逼近。此类方法计算复杂,受流形本身形状影响较大从而稳定性较差。另一类比较有效的做法是添加一些虚拟样本点,使得样本点相对稠密,从而改善降维效果。例如,Zhan等[11]利用样本点到邻域内其他两个点组成连线的垂足来添加样本点,提出了基于邻域线的LLE算法。但该方法并没有考虑流形本身的性质和曲率等因素对降维的影响,添加的虚拟样本点与原样本点之间为线性关系,因此,效果有限,只能针对特定的流形。
为此,我们提出了一种新的基于Biharmonic样条插值的流形学习算法BbMLA,通过非线性的获取插值点来有效改善邻域内样本点的稠密程度,同时插值点又能忠实的保持流形本身的结构和性质。在本文提到的算法中,我们利用Biharmonic样条插值算法[12],首先在样本点的各邻域内做曲面插值,而后根据流形本身的特点和性质,从插值曲面中非线性的选取插值点;然后利用这些插值点与原样本点一起组成新的样本点集,并求取其低维坐标;最后,将原样本点的坐标抽离和表示出来,最终得到原样本点集的低维坐标值。通过对插值点的图示,我们说明了算法得到的插值点与流形的本质结构较为匹配,而且插值点考虑了流形的密度和曲率等因素。在将本文提到的插值算法应用到经典的流形学习算法如LTSA、LLE后,实验结果证实了我们的算法的有效性和稳定性。
1 流形学习中的样本点稀疏问题
流形学习的方法可以分为两类:一类是全局方法(如Isomap),另一类是局部方法(如LLE、LE、HLLE、LTSA等)。由于局部方法只需要考虑流形临近点之间的关系,无须要求流形所对应的低维空间为凸,且计算复杂度较低,因此局部方法有着更广泛的适用对象[13]。
局部保持的流形学习方法正是通过保持邻域内的局部近邻结构来构造全局低维表示,所以,邻域结构的表示和保持程度将直接影响最终的嵌入效果。在刻画流形的局部几何特性时,需要尽可能的保证局部邻域能够同胚于欧氏空间的一个连通开集。显然,邻域越小,邻域的低维结构越明显,近邻结构越容易忠实保持。另一方面,邻域之间需要有足够的交叠以保证全局排列时有足够的联系,这又使得邻域不能过小。这种矛盾一直伴随着流形学习算法,当样本点比较稀疏时,邻域内的局部同胚条件更加难以保持,这就造成了目前绝大多数流形学习算法在样本点较为稀疏时的失效。
图1标示了样本点稀疏程度不同时某一点的邻域结构,稀疏程度不同时,邻域内的线性程度也不同。其中,采样点数据来自于Swiss Roll,星点为从Swiss Roll随机选择的某一个样本点,实心点为采样点为800个点时的邻域点,空心圆点为采样点为100时的邻域点(邻域值为8,邻域包括自身点)。显然,当采样点比较密集时,我们可以认为其局部同胚于一个欧式空间,此时,样本点在由邻域点线性表出时的误差较小。而当采样点较为稀疏时,局部同胚条件较难保持,此时刻画和表示的邻域内的结构信息,便带有较大的误差,从而导致算法效果变差乃至失效。

图1 样本点稀疏程度不同时的邻域点集Fig.1 Selected neighborhood with different denseness of the sample points
对于流形学习算法不能有效处理稀疏样本点集的问题,目前常用的解决方法,是通过插值增加一些新的样本点以使样本点密集。具体来说,是利用样本点有限的邻域点插值出新的邻域点,然后再由这些原有的邻域点和插值出的新的邻域点张成一个线性子空间去逼近原样本点。例如,NL3E方法利用样本点到邻域内其他两个点组成连线的垂足来添加样本点。
这类插值方法一定程度上改善了样本点稀疏时的算法效果。但是这些方法都采用线性插值的方法去产生新的样本点,也就是说,新的邻域点都是原有邻域点的线性组合,从线性代数的理论来说,由插值点和原有邻域点张成的线性子空间与原有邻域点张成的子空间是一样的,因此,也不会改善线性逼近的误差。而且,插值点并没有反应出流形的本质结构和特征,从理论上背离了数据降维的目的。为此,我们利用Biharmonic样条插值法非线性的获取插值点。此时,插值出的样本点不会被原有邻域点线性表示,也就是说,新插值出的样本点不会落在原邻域点张成的线性子空间里,因此,由插值点和原有邻域点张成的线性子空间是原有邻域点张成子空间的真扩展。如图2所示,线性插值方法是从原邻域点张成的子空间内选取合适的样本点作为插值点,而非线性插值方法是从高维空间逼近的角度选取插值点,由这个子空间去逼近样本点会更有效的减少逼近误差。另外,由于是从邻域内曲面重建中非线性的获取插值点,插值出的点能够更好的反映流形的曲面性质而不是平面性质,从而更好的保持和揭示了流形的本质特征。

图2 线性插值与非线性插值方法选取插值点的不同Fig.2 The difference of interpolation points chosen by linear and non-linear interpolation method
2 基于Biharmonic样条插值的流形学习算法
算法主要用于解决样本点稀疏问题,对于稀疏样本点,根据其本质结构特点,利用Biharmonic样条插值方法在样本点的邻域内构造插值曲面,并从插值曲面中选取一定数目的样本点作为插值点。而后,利用这些插值点与原样本点一起作为新的样本点集。待利用各种经典的流形学习算法求得样本点的全局低维坐标后,取出原样本点集的低维坐标。
2.1 Biharmonic样条插值
解决样本点稀疏问题的有效方法之一,是根据流形特点,添加新的插值点。为了合理的构造插值点,我们首先需要用一个光滑的曲面来逼近这些无规则的散乱抽样数据点,即曲面拟合问题;然后从拟合的曲面上选取合适的点作为新样本点。流形上散乱数据的曲面拟合,其难点在于,如何得到邻近点间正确的拓扑连接关系,而正确的拓扑连接关系将有效的揭示散乱数据集所蕴涵的本质形状和拓扑结构。
在众多的曲面拟合算法中,Biharmonic样条插值方法[12]是一种效果较好的曲面构造方法。与其他曲面拟合算法如双三次样条插值和B样条插值算法相比,Biharmonic样条插值方法拟合的曲面较为光滑,局部性能较好,能够根据散乱数据点发现和保持曲面的本质结构和特征,而且算法计算量较小,效率较高[14]。
Biharmonic样条可以对散乱分布的数据进行曲面插值。插值产生的曲面是以各数据点为中心的Green函数的线性组合[12]。Biharmonic方程在不同维空间中的解就是不同维的Green函数。对于D维空间中散乱分布的K个控制点xk,k=1,2,…,K,Biharmonic样条D维插值问题转化为对公式(1)的求解
(1)
其中,▽4为Biharmonic算子,δ为单位冲击函数,W(X)为X位置处的值。
图3为在Twin Peaks样本集上做Biharmonic样条插值方法后从插值曲面上选取部分插值点的图示。

图3 Biharmonic样条插值方法选取的插值点Fig.3 Effect by Biharmonic spline interpolation algorithm
其中,图3(b)中空心圆点为原样本点(原样本点数目为200),实心点为从插值曲面上选取的部分插值点。由图3可以看出,Biharmonic样条插值法得到的曲面,与原流形曲面较为匹配,比较忠实的体现了原流形的特征和结构,并且,插值函数本身动态的考虑了流形的曲率和密度变化等因素。
2.2 插值点的选取
插值点的选取是指从插值曲面上,取合适的点作为新的样本点,并放入样本集中。为了提高插值精度,我们要产生尽可能多的点来逼近原流形曲面。但是,过多的插值点参与到流形学习算法会很严重的影响算法的效率。而且,按照文献[11]的理论,为每一个样本点插入不少于其维数的插值点即可。从直观上考虑,样本点稀疏处,应选择较多的插值点,曲率较大处,应选择较多的插值点。通常,插值点的选取有两种方法,一种为从插值曲面上均匀采样,另一种是根据流形及样本集本身的特点(如样本稠密度和曲率的不同)来抽取样本点。由于Biharmonic样条插值法在插值时,已经考虑了流形局部的密度和曲率等因素,因此,我们只需要选取合适数目的样本点作为插值点。
选出的插值点,有两种利用方式。一种是让插值点和原样本点集组合起来,一起参与流形学习算法;另一种是只利用局部范围内的插值点,来修正每个样本点的局部坐标,但这种方法,不能有效的处理邻域间交叠不够的问题。本文中,我们选取第一种方法。
2.3 BbMLA算法框架
为了解决流形学习算法不能有效处理稀疏样本点的问题,针对线性插值方法的不足,我们提出了基于Biharmonic样条插值的流形学习算法,即BbMLA算法。算法首先选取生成插值点的邻域,然后利用Biharmonic样条插值方法在样本点的邻域内构造插值曲面,并从中选取一定数目的样本点作为插值点。选取插值点后,将插值点并入原样本点集中并利用经典的流形学习算法获取新的样本点集的低维坐标;而后,将原样本点集分离出来从而得到最终的原样本点集得低维坐标。算法过程如表1所示:
算法中,X为原始样本点集,V为新插入点的样本集,L为Biharmonic样条插值时的邻域选取参数,为了保证邻域内的点满足同胚条件,可根据样本点密度或曲率变化动态调整L。λ为从重建曲面中采样时选取的新样本点个数,可为每一个样本点选取不同个数的插值点。MLA为调用流形学习算法得到低维坐标,可选择多种流形学习算法如LLE、ISOMAP、LE、HLLE、LTSA等。

表1 BbMLA算法过程Table 1 Pseudo-code of BbMLA
3 实验及分析
为了更好的比较和分析插值前后算法的效果差异,我们设计了以下实验。实验中,CPU频率为1.86GHz,内存容量为2GB,运行环境为Matlab 7.0。
3.1 插值点效果对比
我们首先对线性插值和非线性插值方法得到的插值点的效果进行了对比。
图4标示了样本点数为200,邻域值取8时的插值点效果对比图,其中(a),(a′),(a″),(a‴)为原始样本点集图,(b),(b′),(b″),(b‴)为线性插值(NL3E为例)后的样本点集图,(c),(c′),(c″),(c‴)为Biharmonic插值算法得到的样本点集图。(b),(b′),(b″),(b‴)、(c),(c′),(c″),(c‴)图中红色圈点为原始样本点,蓝色实点为选取的插值点(并非改变原采样点的颜色向量,在此只是为了区分原采样点和新插值点)。由图4可以看出,通过非线性插值方法插值后的样本点集,较好的保持了流形的本质特征。与线性插值方法相比,得到的插值点更加忠实于流形本身。

图4 插值点效果对比(N=200, L=8)Fig.4 Interpolation points by linear and nonlinear methods(N=200, L=8)
3.2 插值前后流形学习算法效果对比
插值算法可以应用到数据集。我们首先Mani程序中的数据集(Swiss Roll、Punctured Sphere和Twin Peaks),Mani数据集是一种在流形学习中广泛使用的数据集,可以方便的从http://www. math.ucla.edu/~wittman/mani/index.html处免费下载。
图5标示了在原样本点数目为400,邻域取8时,原LTSA算法的效果图以及相应的在插入插值点后的算法效果图。其中(a),(a′),(a″)为原始流形采样图;(b),(b′),(b″)为插值后的采样图,其中红色圈点为原始样本点,蓝色实点为选取的插值点;(c),(c′),(c″)为原LTSA算法效果图;(d),(d′),(d″)为插值后的LTSA算法效果图。由图5可以看出,插值后的算法效果跟原始算法效果相比基本相同,这主要是因为原始采样点比较密集,邻域内基本满足局部同胚关系,故虽然插入的样本点基本保持了流形本身的形状且使得样本点集更为稠密,但对整体效果的影响有限。
图6标示了在原样本点数目为200,邻域取8时,原LTSA算法的效果图以及相应的在插入插值点后的算法效果图。由图6可以看出,原始的LTSA算法得到的降维图,效果已显著下降,这主要是因为原始采样点比较稀疏,邻域值取8时,邻域内的样本点已难以满足局部同胚关系,故得到的降维效果欠佳。插值后,新插入的样本点较好的保持了原流形的本质结构,邻域内的样本点重新较好的满足了局部同胚关系,故插值后的算法取得了较好的效果。
图7标示了在原样本点数目为100,邻域取8时,原LTSA算法的效果图以及相应的在插入插值点后的算法效果图。由图7可以看出,原始的算法已基本失效,而插值后的算法仍保持了较好的效果。这主要是由于插值前的样本非常稀疏,局部很难保持同胚条件,而插值后的新的样本点集有效的克服了这一现象。
当样本点较为稀疏时,为了保持局部同胚关系,我们可适当的降低邻域值。但太小的邻域值会使得邻域间缺乏足够的交叠,从而使得全局排列受到较大影响,甚至导致算法失效。图8标示了在原样本点数目为100,邻域取4时,原LTSA算法的效果图以及相应的在插入插值点后的算法效果图。由图8可以看出,原LTSA算法由于邻域间缺乏足够的交叠,导致算法失效,而插值后的算法,由于添加了样本点,使得邻域间的同胚关系得到较好保持的同时,也增强了邻域间的交叠关系,从而使得算法效果有了较为明显的改善。

图5 Mani数据集插值前后LTSA算法效果对比图(N=400, K=8)Fig.5 Processed results by LTSA with the interpolation algorithm(N=400, K=8)

图6 Mani数据集插值前后LTSA算法效果对比图(N=200, K=8)Fig.6 Processed results by LTSA with the interpolation algorithm (N=200, K=8)

图7 Mani数据集插值前后LTSA算法效果对比图(N=100, K=8)Fig.7 Processed results by LTSA with the interpolation algorithm(N=100, K=8)

图8 Mani数据集插值前后LTSA算法效果对比图(N=100, K=4)Fig.8 Processed results by LTSA with the interpolation algorithm (N=100, K=4)
图9标示了插值前后在SCurve数据集上LTSA算法效果对比图。与在Mani数据集上基本类似,当样本点较为稀疏时,插值算法取得了较好的效果。多个数据集上的效果,说明了我们的算法的健壮性和鲁棒性。
我们的插值算法也适用于其他经典流形学习算法如LLE、HLLE、Diffusion Maps等。图10标示了插值前后LLE算法效果对比图。由图10可以看出,我们的插值算法在LLE等其他流形学习算法中也取得了较好的效果。
同时,我们也做了其他一些高维数据集的实验,如Frey Faces和Handwritten Digits等。算法同样能取得较好的效果。

图9 SCurve数据集插值前后LTSA算法效果对比图Fig.9 Processed results by LTSA to SCurve with the interpolation algorithm

图10 插值前后LLE算法效果对比图(N=200, K=8)Fig.10 Processed results by LLE with the interpolation algorithm(N=200, K=8)
3.3 参数调整及时间复杂度分析
将BbMLA算法应用到实际问题时,可以根据不同流形的特点,调整参数来获得更好的算法效果。在BbMLA算法中,主要有如下几个参数:

λ,插值点个数。从每个插值曲面选取的插值点数目可以不同,插值点数目越多,插值点便越能忠贞的体现流形本身的结构,但过多的插值点会大大增加算法运行的时间。而且,按照文献[11]的理论,为每一个样本点插入不少于其维数的插值点即可。
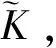
我们提出的算法中,由于需要对每个样本点做曲面插值和插值点的选择,并最终扩展了样本点集来参与流形学习算法,这导致算法的运行时间较长。表2中,我们比较了几种流形学习算法插值前后的运行时间(s),其中数据集取自Swiss Roll流形,采样点为200,邻域为8。由表2可以看出,插值算法和增加的插值点大大增加了算法的运行时间。可行的解决办法,一是选择合适的标志点而不是所有数据点的邻域来做曲面插值,二是选择插值点时在保持较好降维效果的同时尽可能选择较少的点;三是插值后的流形学习算法设定合适的邻域值,适当的减小邻域会降低算法的运行时间。

表2 不同插值点时几种流形学习算法运行时间对比Table 2 Comparison of running time with different interpolation points
4 结 论
近年来,流形学习方法在数据挖掘、机器学习、图像处理和计算机视觉等多个研究领域吸引了广泛的关注并取得了长足的发展。但当样本点较为稀疏时,这些流形学习算法往往效果变差甚至失效。解决此问题的有效方法,是根据流形特点增加一些插值点。但已有的算法均采用线性插值的方法获取插值点。从线性代数的理论来说,由插值点和原有邻域点张成的线性子空间与原有邻域点张成的子空间是一样的,新的插值点不会改善线性逼近的误差。而且,插值点并没有反应出流形的本质结构和特征,从理论上背离了数据降维的目的。本文利用Biharmonic样条插值法非线性的获取插值点,新的插值点能有效的改善稀疏样本集的局部结构,并且插值点能较好的体现流形本身的结构和性质。在将本文提到的插值算法应用到经典的流形学习算法如LTSA、LLE后,实验结果证实了我们的算法的有效性和稳定性。
值得注意的是,我们提出的算法中,由于需要对每个样本点做曲面插值和插值点的选择,并最终扩展了样本点集来参与流形学习算法,这导致算法的运行时间较长,尤其是对于较高维数的样本集,算法的运行时间更加难以接受。由此,如何有效的提高算法的执行效率将是本文未来的研究内容。
参考文献:
[1] TENENBAUM J B, SILVA V DE, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction [J]. Science, 2000, 290(5000): 2219-2323.
[2] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000, 290(5000): 2323-2326.
[3] DONOHO D, GRIMES C. Hessian eigenmaps: locally linear embedding techniques for high-dimensional data [J]. Proceedings of the National Academy of Sciences, 2003, 100(10): 5591-5599.
[4] ZHANG Z Y, ZHA H Y. Principal manifolds and nonlinear dimension reduction via local tangent space alignment [J]. SLAM Journal of Scientific Computing, 2004, 26(1): 313-338.
[5] BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation [J]. Neural Computation, 2002, 15: 1373-1396.
[6] KARBAUSKAITЁ R, KURASOVA O, DZEMYDA G. Selection of the number of neighbors of each data point for the locally linear embedding algorithm [J]. Information Technology and Control, 2007, 36: 359-364.
[8] WEN G, JIANG L, WEN J, et al. Performing locally linear embedding with adaptable neighborhood size on manifold [C]// 9th Pacific Rim International Conference on Artificial Intelligence, Springer Verlag, 2006: 985-989.
[9] WU S, QUAN X W, CHEN X C. CN-isomap algorithm for nonlinear dimensionality reduction of sparse data [J]. Mathematics in Practice and Theory, 2010, 17(40): 182 -188.
[10] SONG X, YE S W. Data dimensionality reduction algorithm when source data is spare [J]. Computer Engineering and Application, 2007, 43(28): 181-183.
[11] ZHAN D C, ZHOU Z H. Neighbor line-based locally linear embedding [J]. PAKDD, Springer Verlag, 2006: 806-815.
[12] SANDWELL D T. Biharmonic spline interpolation of GEOS-3 and SEASAT altimeter data [J]. Geophysical Research Letters, 1987, 2: 139-142.
[13] ZHANG T H, TAO D C, LI X L. A unifying framework for spectral analysis based dimentionality reduction [C]//International Joint Conference Neural Networks, 2008: 1670-1677.
[14] WANG Y T, DONG L F, NI K. Image morphing algorithm based on Biharmonic spline interpolation and its implementation [J]. Journal of Image and Graphics, 2007, 12(12): 2189-2194.
