基于SAA的光伏系统MPPT技术研究*

周超林，付 青，邓幼俊

(中山大学 物理科学与工程学院，广东 广州 510006)

太阳能作为新能源的一种，由于具有可持续、易获取和环境友好等优点，而受到各国的重视[1]。

由于多种原因，太阳能发电面临效率不高和初装费用较高的问题。而太阳能高效转换需从两方面考虑，一方面是太阳光到电功率转换效率，另一方面则是控制器的提取效率，即需控制从电池板中尽可能多的提取电能[2]。本文主要从控制的角度对运行在非均匀光照情况下的太阳电池的提取效率进行优化。

MPPT(Maximum Power Point Tracking)是控制从太阳电池中尽可能提取多电能的算法。经过多年的研究，已取得了较大进展。文献[3]详细介绍了现有的几类MPPT方法。

第一类是传统算法，有爬坡(HC)算法、扰动(P&O)法、恒定电压(CV)法、增量电导(INC)法。这些算法都是针对单个电池提出的算法，特点是实现简单，但都存在抗干扰性差、效率低、无法应对多云天气的问题。

第二类是传统算法的简单改进，主要有三点扰动法、变步长爬坡法、变步长扰动法，这类算法是MPP波动的解决方案，实现较为简单，且能获得更多的能量。但其也无法应对多云天气的MPPT，易造成误判。

第三类是基于新理论提出的方法，有模糊逻辑(FLC)算法、神经网络(NN)算法等。这类算法能够很好的跟踪最大功率点，但运算量大、实现复杂，而且在多云天气下仍无法很好跟踪最大功率点[4]。

由于上述算法在非均匀光照下都存在一定程度“失效”，因而无法很好的应对在非均匀光照下的MPPT，为解决该问题，本文从电池在非均匀光照下的特征出发，通过先分析后解决的思路，试图寻求一种计算量较小、速度快、能较好应对非均匀光照下的MPPT。

1 电池仿真与MPPT分析

1.1 太阳电池单元的数学模型

文献[5]提出了单二极管的太阳电池等效电路模型，该电路模型如图1所示，其将太阳电池简化为一个PN节。

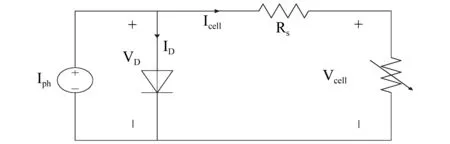
图1 太阳电池等效电路模型Fig.1 Solar cell equivalent circuit model

该模型的数学描述如表达式(1)-(7)所示：

Vcell=VcellRs

(1)

Icell=Iph-ID=Iph-Io(eKpv(vpv+Ipv·Rs)-1)

(2)

(3)

(4)

(5)

(6)

其中，Vcell和Icell是太阳电池的端电压和端电流，Ipv即为Icell，VD和ID分别是内部二极管电压和电流，K为波尔曼兹参数，Kpv=q/pKT中q=1.6×10-19C为电子电荷量，T为电池温度，p=1.3是单晶硅太阳电池在理想状态下的p-n节特性系数，Iph是光电流，Isc是参考环境下的短路电流，KI短路电流的温度系数，Tr为参考温度，ITT是在参考温度Tr下的反向饱和电流，λ日照强度(单位MW/cm2)，Vg是太阳电池的半导体带隙电压，对于硅电池而言，其数值为1.12 EV。

1.2 电池阵列在均匀和非均匀光照下的模型

由单个太阳电池数学模型可拓展至光伏阵列[6]。假设某一光伏阵列，串联PV单元的个数为Ns，并联个数为Np，则在均匀光照下该阵列模型的电流可以用(2)来计算。

(7)

光伏阵列输出功率则可通过(7)与电池板输出电压Vpv相乘来计算。于是有：

(8)

根据上面建立的关系表达式，搭建Simulink下的仿真模型，选取表1中的电池参数进行仿真，得太阳电池板在参考温度和参考光照情况下的特性曲线图如图2所示。

表1 太阳电池板参数

由太阳电池数学模型知，光照非均匀情况下，不同组件输出电流由于光照强度不一致而不一样。因此，在非均匀光照下式(7)(8)无法正确描述光伏阵列的正常运行情况。光强非均匀下的电池模型在文[7]中已经做了相应的研究，本文就不再赘述，仅通过仿真其特性曲线，来说明其在非均匀光照下的运行特点。

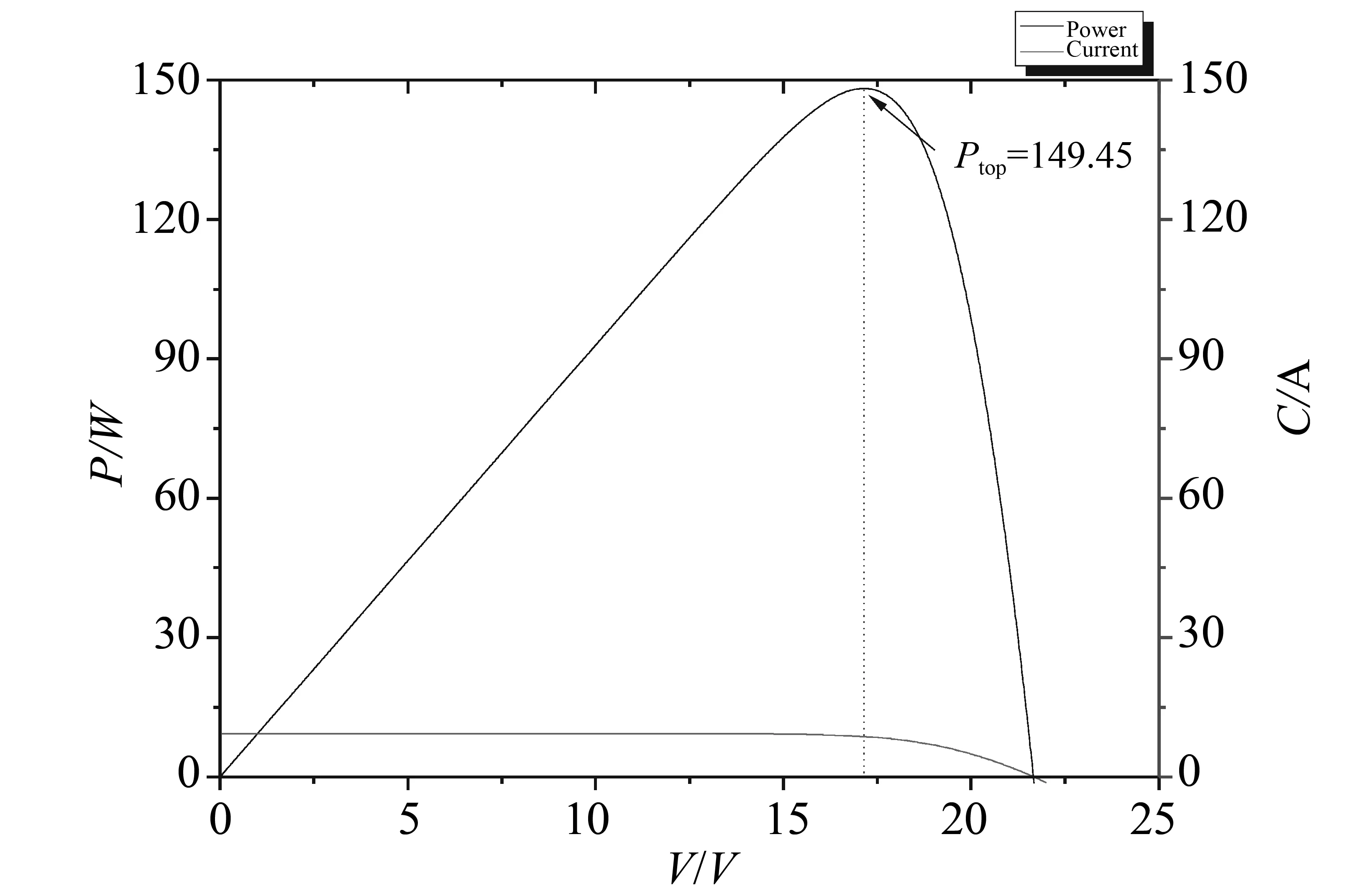
图2 该太阳电池特性曲线Fig.2 Characteristic curves of the solar panel

电池非均匀光照形式有多种，总的来说，对称和非对称两种类型。按照表1的参数搭建在非均匀光照下的仿真模型，考察下面三种遮光模式。

1)一列串联线路中12个组件遮光，其光照强度为0.4个标准光照强度，剩余单元均处于标准光强下；

2)一列串联线路中18个组件遮光，其中9个光强为0.6个标准光照强度，9个光强为0.4个标准光照强度，剩余单元均处于标准光强下；

3)两列组件均有遮光，其中一列遮光组件数为24，光强为0.6个标准光强，另一列遮光组件数为12，光强为0.4个标准光照强度，剩余单元均处于标准光强下；

图3是上述3种方式下的仿真结果，(a)、(b)、(c)分别对应方式1)、2)、3)的电池特性图。由图可总结出该太阳电池在非均匀光照下特性曲线有如下基本特征。

1)伏安特性曲线(I-V曲线)呈现多个膝型平台，功率电压曲线(P-V曲线)呈现局域多峰状。

2)开路电压Voc基本不变，保持在21.6 V附近。短路电流Isc也基本不变，保持在9.3 A附近。

3)功率曲线的峰值数与伏安特性曲线膝行平台数均正比于太阳能面板上所接受到的太阳光强度种类。即光照强度层次越明显，功率曲线的峰值越多、伏安特性曲线膝行平台数目越多。

4)遮光情况下的最大功率的分布具有随机性，无法定性地确定在某一区域内。即功率曲线的多峰值在自变量输出电压Vo下的分布具有一定的随机性。

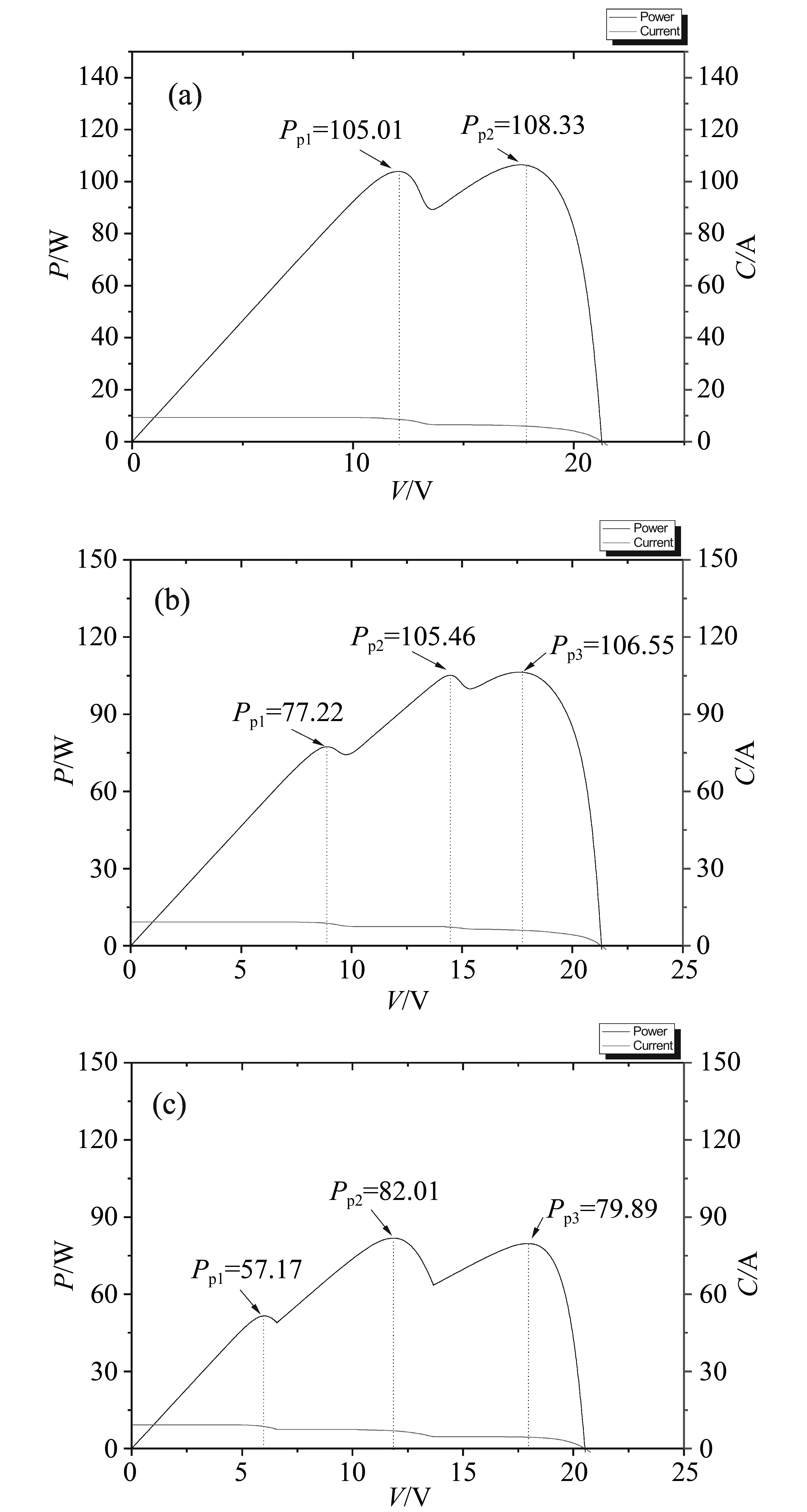
图3 非均匀光照下该太阳电池特性曲线Fig.3 Characteristic curves of solar panel under non-uniform illumination

1.3 MPPT分析

由上一节的分析可知，太阳电池输出功率总在某个特定输出电压能达到最大值，该点即为最大功率点。MPPT技术是通过DC/DC变换的方法使得电池一直工作在最大功率点附近，以从电池中抽取尽量大的功率[8]。

根据太阳电池的运行状态，其MPPT可以分为以下几种类型：

1)均匀光照情况下，太阳电池P-V曲线呈现出单峰值波形。忽略温度等因素对电池的影响，电池MPPT可通过引言中提到的所有算法实现。

2)非均匀光照情况下，太阳电池P-V曲线呈现出多峰值波形。在该种情况下，由于现行大多算法基于单峰值的跟踪，无法顾全全局，往往会跟踪到其中的某一个峰值，达到局部最优而非全局最优。

3)从均匀光照跳到非均匀光照情况下，由于曲线在从原最大功率点出发，在进行局部峰值扫描时可能处于局部最优的山坡上，因而可能无法跟踪到最大功率点。

4)从非均匀光照到均匀光照下，该情况最终运行在单峰值的曲线上，MPPT即为均匀光照下的跟踪，仅出发点位于原最大功率点，显然可快速跟踪到最大功率点。

5)从一种非均匀光照情况变换到另一种非均匀光照情况下，假设前面是跟踪在最大功率点，到另一状态，可能最大功率点在另一区间，采用常规方法可能导致最终跟踪到局部最优。

通过以上分析，可知非均匀光照下的MPPT，需要解决的问题主要有以下两个。

1)遮光检测，若初始运行在均匀光照下，后某个时刻发生突变，变为非均匀光照，往往控制方式就需做相应的变动。然而，本文侧重另一问题，该点就不多作讨论。

2)多峰值跟踪。由于传统方法及其优化都是基于特性曲线的斜率特性特性，无法实现多峰值MPPT。而基于新技术的控制算法复杂，实现困难，且也无法完全解决遮光情况下的MPPT问题。因此，寻求一种相对有效的算法来实现系统在初始遮光情况下的MPPT意义非比寻常。

2 SAA及其MPPT应用

2.1 SAA

退火是将金属材料加热后再经特定速率冷却，目的是增大晶粒的体积并减少晶格中的缺陷。加热前，材料中的原子原来会停留在使内能有局部最小值的位置，加热使能量变大，原子会离开原来位置，而随机在其他位置中移动，使得原子有较多可能可以找到内能比原先更低的位置[9]。

模拟退火(SAA)即模拟金属煅造过程中的退火，通过概率的方法试图在空间寻求最优解。具体而言，即初始状态不稳定(如同高温态)，对当前状态进行随机改变，若改变状态更好，则选择改变后状态为当前状态，否则，以一定概率exp(-Δt′/T)选择改变后的状态。

SAA与初始值无关，求得的解与初始解状态S(算法迭代的起点)无关，而且具有渐近收敛性。已在理论上被证明是一种以概率l 收敛于全局最优解的全局优化算法[10]。

标准的模拟退火算法的一般过程如下[11]：

1) 给定初始温度t=t0,随机产生初状态s=so,令k=0。

2) Repeat。

(a) Repeat。

(a1) sj=Genete(si) 产生新状态;

(a2) if min{1,exp{-C(sj)-C(si)}/ts}}random(0,1) si= sj;

(a3) Until 抽样稳定准则满足。

(b) T(k+1)=update(T(k))，退温，并令k = k+1。

3) Until算法终止准则满足。

4) 输出搜索结果。

2.2 基于SAA的MPPT控制

由1.2分析可知，电池工作在非均匀光照下时，其P-V曲线呈现多峰值分布，且峰值呈随机分布.因此，MPPT问题实质是求解全局最优。外界保持在非均匀光照情况，若采用传统算法，初始状态在局部最优附近时，会掉入局部最优。当无快速的确定性算法找到最优解，而穷举所有情况会消耗较多资源或时间时，随机优化算法会是一个较好的选择。即可通过较低成本接受一个看得过去的优化结果。改进的MPPT算法是在增量电导法的基础上加入SAA，以提高光伏发电系统在非均匀光照下的转换效率。

由前分析可知，即使在非均匀光照情况下，开路电压基本保持不变。因此，随机电压生成可以采用[0,1]随机数与开路Voc的乘积来得到。考虑Buck电路的响应并不快，跟踪时应尽量减少当前到下一点的跟踪距离，因此随机电压获取采用正序抽取随机电压逆序排列的方式。

图4是基于SAA的MPPT控制框图。事先生成符合要求的逆序电压随机队列，让系统直接跟踪到第一个随机电压，然后进行估计，若新的电压点能够满足功率最大条件，则跟踪到该山峰的峰顶。最后通过PI环节来改善控制性能，输出PWM波到控制管。

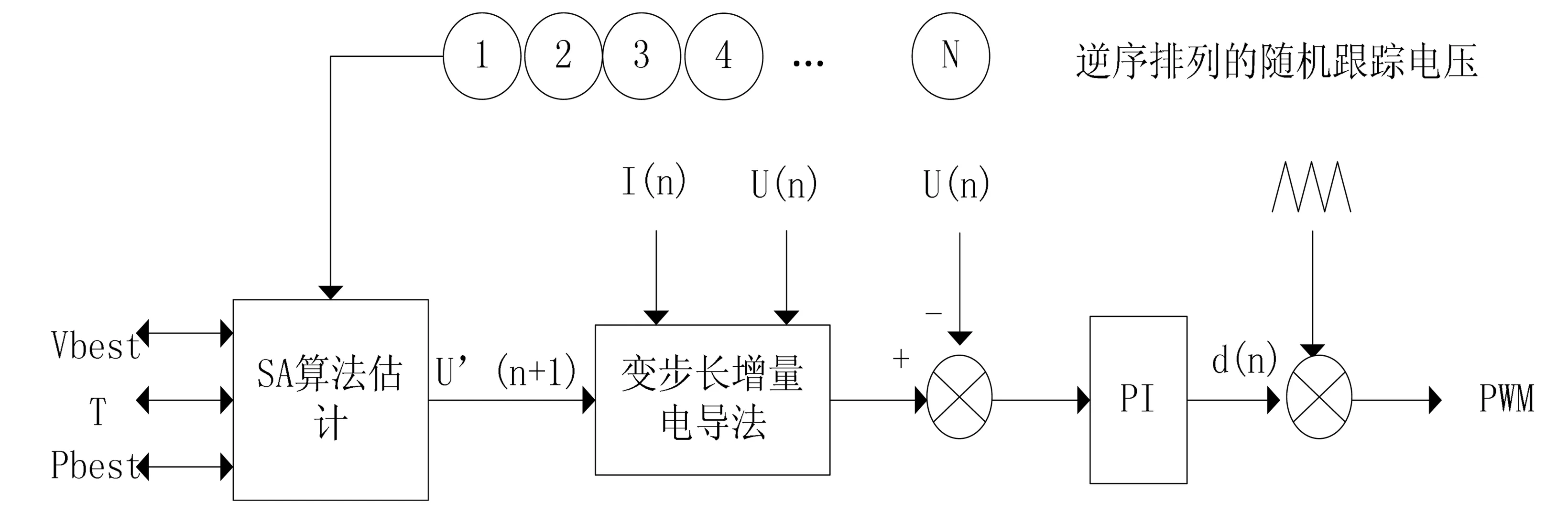
图4 基于SAA的MPPT控制框图Fig. 4 Block diagram of SAA-based MPPT method

图5为基于SAA的MPPT程序流程图。其中T为温度，起始需进行初始化，r是降温系数，设置为小于1.0的常数。Vopt是当前跟踪到的最优功率点，初始化为开路电压Voc。若随机电压经过SAA的概率估计时被舍弃，则降低温度，直接进入随机队列，试探下一个随机电压值。而若被接受，那么通过增量电导法跟踪到一个Vmax电压，下次取随机电压时需忽略比Vmax大的电压值。这样循环进行下去，直到队列被取完或者温度达到目标温度。SAA关键在于随机电压点数的确定。若光照强度层次多，需增加随机预测电压数目；若光照层次少，则无需过多的随机预测电压数目。

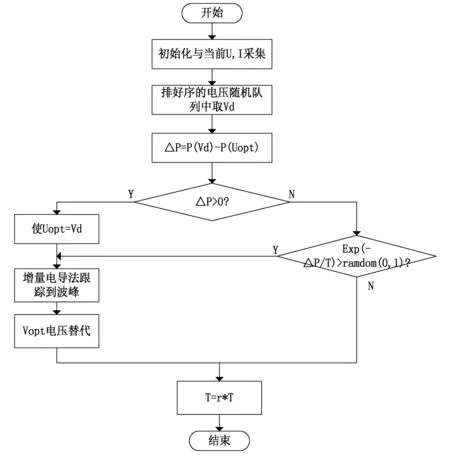
图5 基于SAA的MPPT算法流程图Fig. 5 Flow of SAA -based MPPT method

3 系统仿真与结果分析

在Simulink下搭建1.2节的第3种非均匀光照条件的太阳电池模型，连接buck电路，用S函数来实现基于SAA的MPPT。

图6仿真为基于SAA的最大功率跟踪Simulink仿真模型[12]。SAA中初始化温为T=Pmax/log5= 117，取降温系数r=0.5，随机电压序列个数N=10，退出温度满足T<0.01，单次抽取随机温度便退火一次，若跟踪电压低于当前运行电压，跳过一格取后面随机电压值。表2给出了该仿真模型的主要电路参数。

表2 Buck电路参数

为方便对比，本文通过修改S-Function建立了几个对照组。仿真结果如图7所示。其中，(a)、(b)、(c)分别对应基于SAA、传统增量电导法和全局搜索的MPPT波形[13-14]。

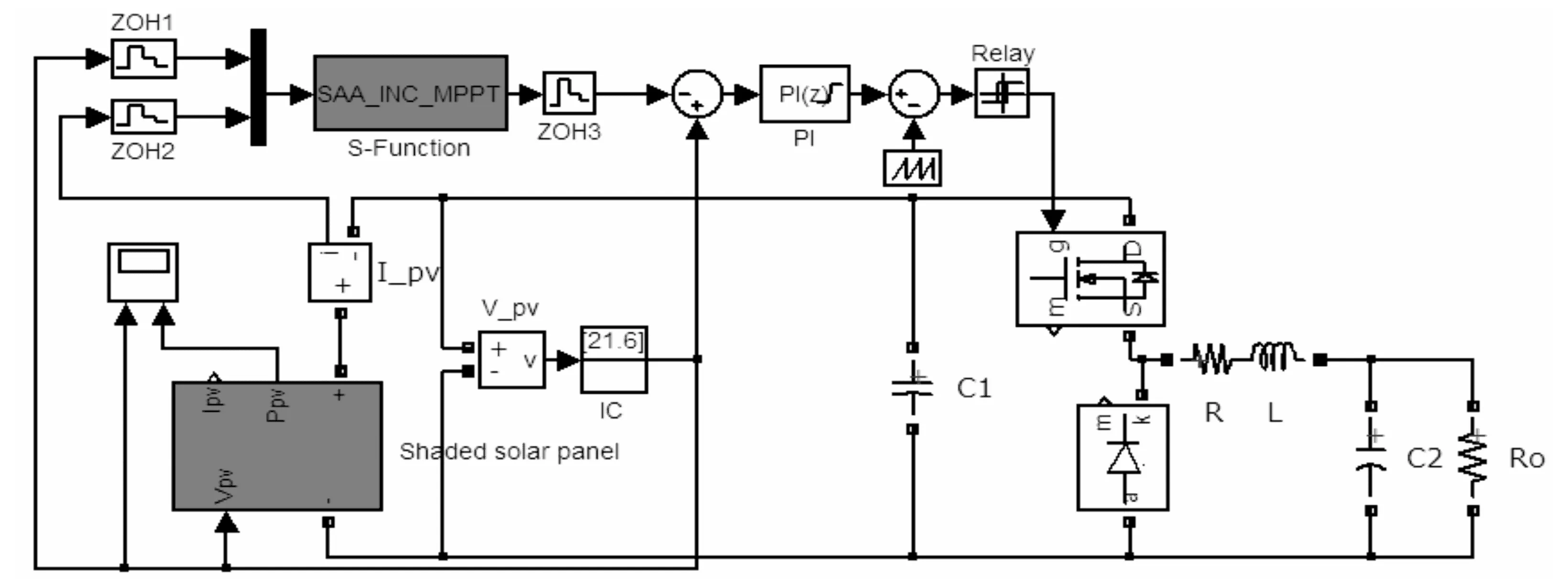
图6 基于SAA的光伏系统仿真图Fig.6 Simulation of PV system based on SAA

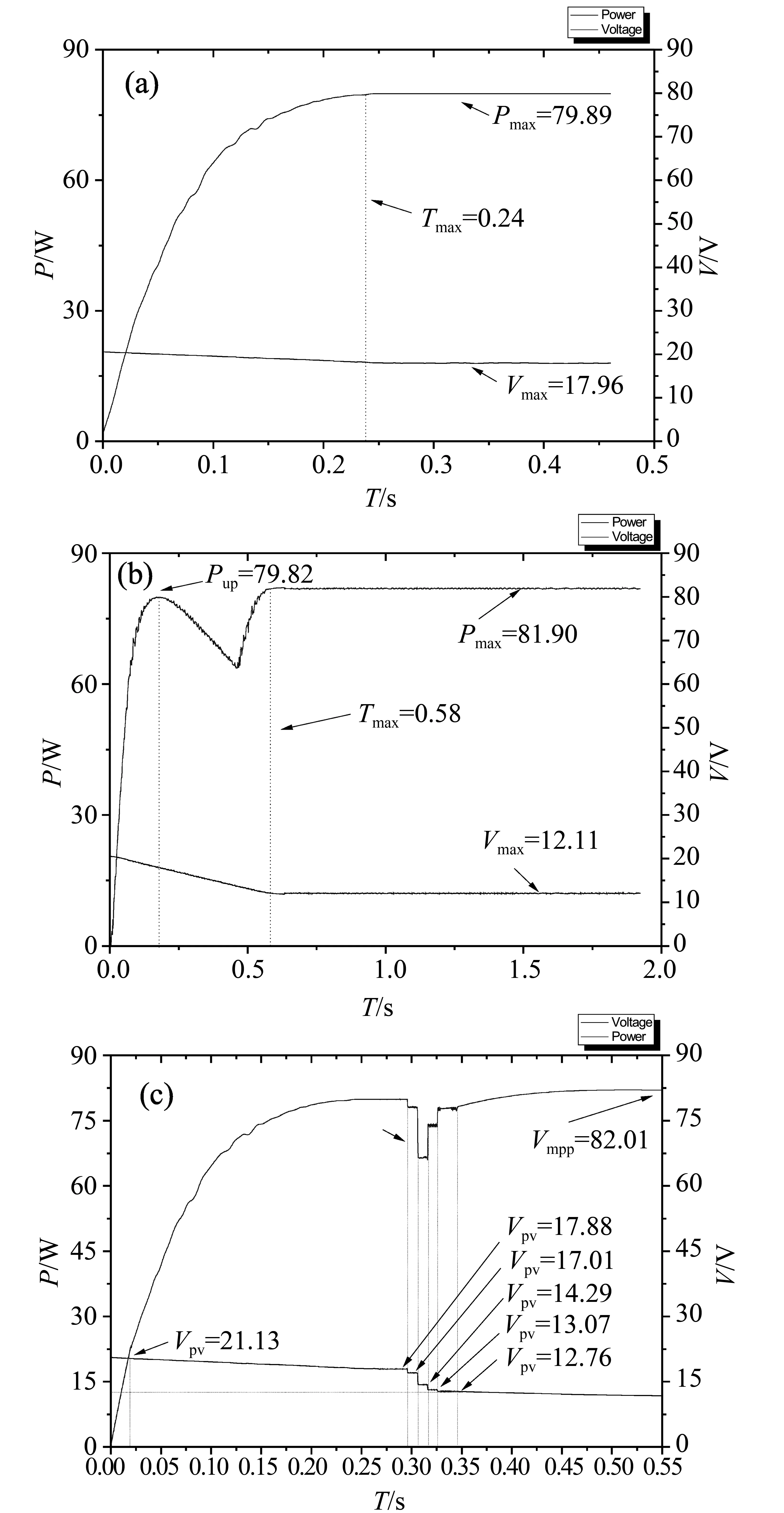
图7 Simulink下不同算法的MPPT波形Fig.7 Simulation results obtained through different MPPT algorithms

图7(a)是常规增量电导法跟踪，由于起点是开路电压，因此其跟踪到了位于开路电压所处山峰的峰顶，即Ppv= 79.89 W，而非全局的最大功率点Ppv=82.01 W，因此该方法的结果并非最优。图7(b)采用的是全局扫描的方法，由于电池有36*2块，因此出现的最大光照层次数目是72，在整个电压区间将其等份，设置0.5的裕度，因此分割电压为0.15 V，该方法相对第一种要优越，波形最终也跟踪到了最大功率点附近，但考虑到峰值的随机性，该方法并不总能跟踪到最大功率点的，更大可能出现误判现象。(波形出现的并未跟踪到低于Vpv=11.46 V电压的缘故是Buck电路无法降低负载的大小)而图7(c)是基于SAA的MPPT，它的跟踪按生成的逆序随机电压方向进行，图中分别标出了各处的随机电压值，通过判断定则决定是否继续采用增量电导法跟踪。由于具有随机预测估计与增量电导法的两重优势，在光照层次不太多时候，该算法能较快的跟踪到电池最大功率点。

表3给出了三种不同算法在该情形下的跟踪效率比较，增量电导法明显要比其他两种算法快，但效率也是最低的。采用SAA的MPPT相对而言效率最高(功率精度为0.01的情况下，理想地认为基于SAA的MPPT算法达到100%的效率)，跟踪时间相对全局搜索有明显优势。

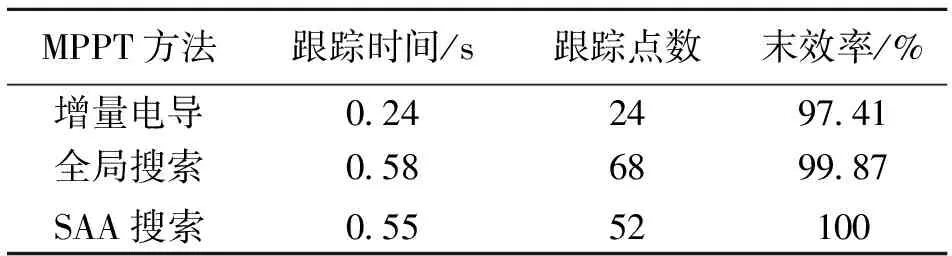
表3 不同跟踪算法的效率对比Table 3 Comparison of different MPPT algorithms in terms of efficiency

4 结 论

本文提出了一种基于SAA的MPPT控制算法，该算法是在增量电导法的基础上加入SAA随机策略，以概率形式估计跟踪电压的有效性，以此判断跟踪的大体方向，在快速跟踪的基础上，兼顾系统的全局最优，有效地避开局部最优，跟踪到非均匀光照下光伏电池的MPP，减少了功率损耗。仿真结果证明该算法的有效性，改进后的算法能够弥补常规增量电导法在非均匀光照条件下的不足，提高系统的跟踪精度。

然而，由于该算法的复杂度要高于传统跟踪算法，在光照均匀情况下应尽量避免该算法。若光照强度的层次多且持续时间短时，并不建议使用SAA的MPPT。由于SAA基于随机预测，层次过多可能造成跟踪时间过长，导致没跟踪到MPP就已经切换到均匀光照下，而造成电能浪费。

本文主要解决长时间非均匀光照下最大功率跟踪问题。后续需研究光照强度跳变的检测问题。

参考文献：

[1] 王秋林,侯延爽.环境与气候挑战中我国电力发展的战略[J]. 生态经济,2009,01:308-312.

[2] 陈晓高,付青,余世杰等.基于自抗扰控制的光伏并网功率调节系统[J].中山大学学报:自然科学版,2009,48(2):49-53.

[3] 崔 岩,蔡炳煌,李大勇,等.太阳能光伏系统MPPT控制算法的对比研究[J].太阳能学报,2006,27(7): 535-539.

[4] 马贵龙.光伏并网逆变器MPPT及谐波抑制功能的研究[D]. 中山大学,2012:6-10.

[5] KIM I S, KIM M B, YOUN M J. New maximum power point tracker using sliding-mode observer for estimation of solar array cur-rent in the grid-connected photovoltaic system[J]. IEEE Trans Ind Elec-tron,2006,53(4):1027-1035.

[6] AHMAD A N, RACHED D. Efficiency optimization of a DSP-based standalone PV system using fuzzy logic and dual-MPPT control [J]. IEEE Transactions on Industrial Info- Rmatics,2012,3(8):573-584.

[7] 刘晓艳,祁新梅,郑寿森,等. 局部阴影条件下光伏阵列仿真模型的研究[J]. 系统仿真学报,2012,24(5): 1125-1131.

[8] HIYAMA T, MEMBER S. Evaluation of neyral network based real time maximum power tracking controller for PV system[J]. IEEE Transactions on Energy Convention,1995,10:24-33.

[9] 赵俊学. 冶金原理[M]. 西安：西北工业大学出版社，2009:121-143.

[10] DEKKERS A, AARTS E.Global optimization and simulated annealing[J]. Mathematical Programming(0025-5610), 1991, 50(3):367-393.

[11] 刘春波. 混合模拟退火算法的研究及其在电机优化设计中的应用[D]. 中山大学,2010:4-14.

[12] 龚纯,王正林. 精通MATLAB最优化计算[M].北京：电子工业出版社， 2012:270-310.

[13] 王敏.光伏系统中最大功率点跟踪系统的研究[D]. 武汉工程大学,2012:28-32.

[14] 项丽,王冰,李笑宇，等.光伏系统多峰值MPPT控制方法研究[J]. 电网与清洁能源,2012,28(8):68-72.