以障碍物凸角点为中继源的欧氏距离变换算法*

张青年

(中山大学地理科学与规划学院, 广东 广州 510275)

距离变换是一种计算背景像元的距离的过程，其计算结果是一幅距离图像，标识各个背景像元到最近的特征像元(源)的距离[1]。常用的距离有棋盘距离、街区距离、倒角距离和欧氏距离。其中，棋盘距离、街区距离、倒角距离等非欧氏距离是对欧氏距离的一种近似。已有的欧氏距离变换算法在提高距离变换的精确性、简单性和时间效率等方面进行了大量研究[2-12]。但这些距离变换算法通常都没有考虑障碍物的阻隔作用，所得距离为两点间的直线距离。在存在河流、山丘等障碍物的地理空间中，两点间的实际可通行路径需要绕过障碍物，其路径长度大于直线距离。因此，普通距离变换得到的距离值与实际可通行距离存在一定差距。

如果一个地理空间中存在若干个障碍物，该地理空间是一个非凸域。非凸域中两点之间的距离被称为“测地距离(geodesic distance)”，也称为“大地距离”[13]。如图1所示，面目标A中有一个洞。对于面目标A而言，A中任意两个相异点P1和P2之间的测地距离为包含于A中的该两点间最短路径的长度。相应地，非凸域中的距离变换被称为“测地距离变换(geodesic distance transform)”[14]。

目前已有少数学者研究了测地距离变换算法[14-18]。其中，文献[14-17]采用了以源为中心的圈层传播算法，文献[18]采用了光栅扫描算法。文献[17-18]都引入了中继源来计算测地距离。但由于中继源并不在最短距离传播路径上，因而存在较大的计算误差。

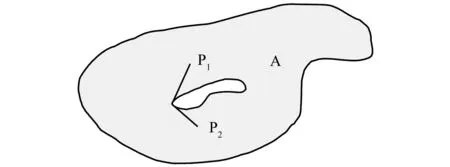
图1 测地距离Fig.1 Geodesic distance

本文将障碍物凸角点作为中继源，采用蛮力算法进行测地距离变换。由于障碍物凸角点位于计算测地距离的最短路径上，因此距离偏移量为0。本文首先讨论测地距离变换中的中继源选择问题，然后利用障碍物凸角点设计了新的测地距离变换算法，再后分析了新算法的实验结果。

1 距离传播路径上的中继源

距离变换可以看作是一个将光线从源逐步传递到周围的背景像元并计算源到背景像元的距离的过程。为简便起见，本文将这一过程称为距离传播。在障碍空间中，从源出发的光线必须绕过障碍物才能到达位于障碍物背后的像元。在前人的研究中，都是将障碍物附近的某个背景像元作为中继源，从源出发沿直线路径到达中继源，再经其他中继源沿直线路径到达目标像元。例如，文献[17]将障碍物背后的某个背景像元设置为中继源，称为局部最近的不可见像元(Locally Nearest Hidden Pixel, LNHP)。LNHP需同时满足5个条件：属于背景像元、有一个8-邻居为障碍物像元、被障碍物遮挡、有一个8-邻居为背景像元，到源的距离小于8个邻居像元的距离。

类似地，以障碍物前方或后方的其他背景像元为中继源也会存在计算误差[18]。产生距离误差的原因在于从源到障碍物后方的背景像元的最短距离传播路径不经过作为中继源的背景像元的中心点。

实际上，最短距离传播路径经过障碍物的凸角点，在凸角点处发生转折。例如，在图2中，从源O到背景像元Q的最短可通行路径在障碍物像元B的角点0和角点3处发生转折。障碍物像元B位于一个条带状障碍物的端点处，而其角点0和3是像元B上的两个凸角。因此，本文以障碍物的凸角点作为中继源，使距离传播路径紧贴障碍物绕转到障碍物背后的不可见像元。

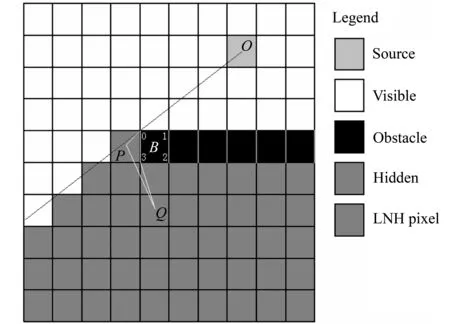
图2 LNHP和距离误差Fig.2 LNHP and distance error

2 测地距离变换新算法

新算法将障碍物凸角点作为中继源，在可见性判断基础上采用蛮力算法计算障碍物凸角点和各个像元到源的测地距离。

2.1 障碍物凸角点的识别

一种方法是将障碍物像元转换为矢量图形，再利用多边形顶点凸凹性识别算法提取障碍物凸角点。可将障碍物像元表示成矢量单元格，再将相邻的矢量单元格合并成一个障碍物多边形，即可分析多边形边界上各个顶点的凸凹性，从而提取障碍物凸角点。

本文不进行栅-矢转换，而是直接依据障碍物像元的邻接关系提取障碍物的凸角点。显然，障碍物的凸角点位于障碍物边缘，其所在的障碍物像元必须与背景像元(或源)相邻。进一步分析，凸角点位于障碍物边缘的凸起处，也就是该角点位于1个障碍物像元和3个背景像元的交点处。设存储图像的数组为P[M, N]，像元的左上角、右上角、右下角和左下角分别编号为0、1、2和3，对于任意像元P[i,j]， 采用以下准则进行判断：

if (P[i,j]是障碍物)

{

if(P[i,j-1]、P[i-1,j-1]和P[i-1,j]都不是障碍物)

{P[i,j]的角点0为凸角点; }

if(P[i-1,j]、P[i-1,j+1] 和P[i,j+1]都不是障碍物)

{P[i,j]的角点1为凸角点; }

if(P[i,j+1]、P[i+1,j+1]和P[i+1,j]都不是障碍物)

{P[i,j]的角点2为凸角点; }

if(P[i,j-1]、P[i+1,j-1]和P[i+1,j]都不是障碍物)

{P[i,j]的角点3为凸角点; }

}

如图3所示，像元A的角点0和3、像元D的角点3、像元E的角点2、像元I的角点1和2将被识别为障碍物凸角点。

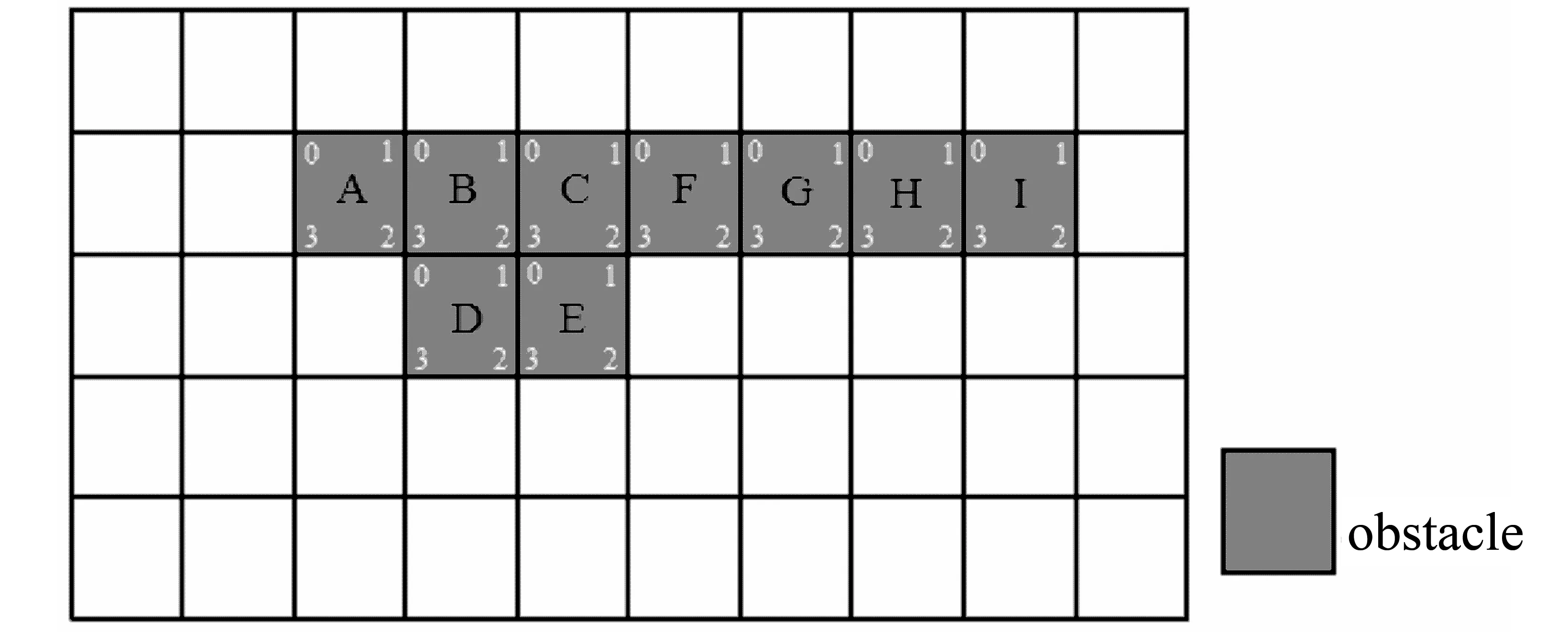
图3 障碍物的凸角点Fig.3 Convex corners on obstacles

2.2 可见性判断方法

在距离传播计算过程中，必须检测源(或中继源)相对于目标像元是否可见。若源(或中继源)可见，则沿直线路径传播距离到目标像元；否则，需引入新的中继源，距离传播路径在障碍物附近发生转折，并经过中继源继续传播距离到目标像元。

可见性判断算法有文献[16]基于障碍物的角度排序的测试算法，文献[17]基于LNHP的障碍物遮蔽角的测试算法，以及文献[18]基于直线全路径栅格化的公共源检测方法。由于文献[18]方法的检测对象可以是像元中心点、角点和其他任意点的点对，本文采用该方法判断可见性。其算法原理是从目标像元P开始向源src反向栅格化，检测P和src的连线是否经过障碍物像元。如果沿直线检测过程中遇到障碍物像元，则src对于P而言不可见；否则，没有遇到障碍物，则判定像元src相对于P可见。该算法并不需要检测P和src连线上的所有像元，其时间复杂度为常数阶[18]。如图4(a)所示，从背景像元P开始朝着源src方向检测，在第一个转折处的两个像元的源都是src，则可判定src对于P可见，退出检测过程。如图4(b)所示，如果第一个转折处的两个像元不是障碍物但其源不都是src，则继续向前检测，没有遇到障碍物，并且在第二个转折处的两个像元的源都是src，可判定src对于P可见，退出检测过程。

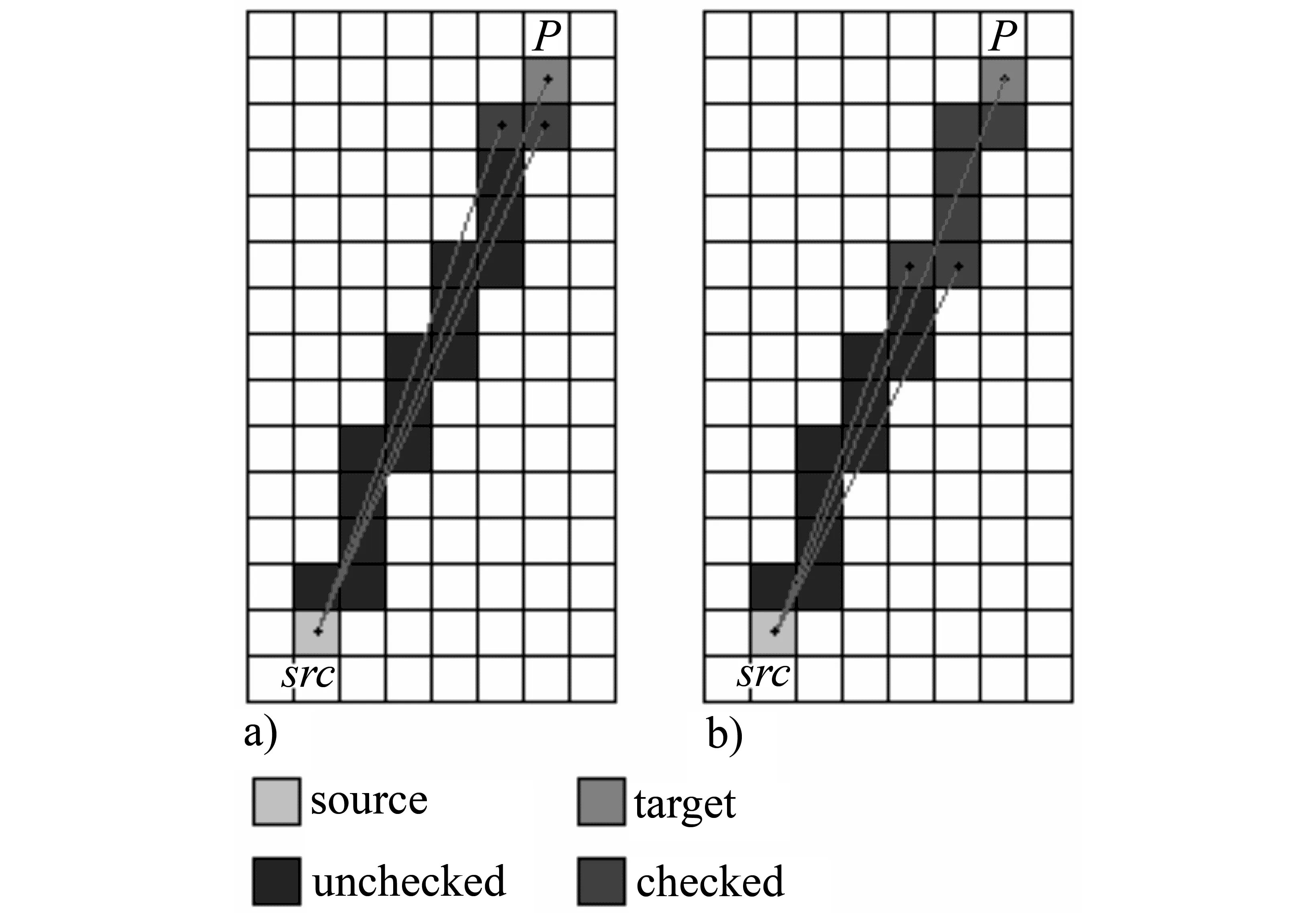
图4 判断目标像元的可见性Fig.4 Check visibility of target pixel

2.3 距离计算步骤

首先计算各个中继源的测地距离，再逐个背景像元计算其距离。

1)遍历中继源序列，计算其测地距离。

构造一个链表srcList，其元素为结构类型sturct{ IPoint pt; double dist; }。插入所有源和中继源，以下统称为“源”。其中，源的距离dist为0，中继源的距离dist初值为极大值D。对srcList进行多轮遍历，更新源的距离值，直到距离没有变化为止。算法的基本流程如下：

do{

置flag为false;

依次取srcList的元素srcList[i];

{

依次取srcList的元素srcList[j];

{

计算newDist = srcList[j].dist + srcList[j].pt与srcList[i].pt之间的直线距离;

if (newDist>=srcList[i].dist) continue;

判断srcList[j]对于srcList[i]是否可见;

如果可见

{

srcList[i].dist = newDist;

置flag为true;

}

}

}

} while (flag)

2)采取光栅扫描方式逐个像元计算其测地距离。算法的基本流程是：

逐行逐列遍历像元阵列元素P[i, j];

{

依次取srcList的元素srcList[k];

{

if (P[i, j]是障碍物像元) continue;

计算newDist = srcList[k].dist + srcList[k].pt与P[i, j]之间的直线距离;

if (newDist>= P[i, j].dist) continue;

判断srcList[k]对于P[i, j]是否可见;

如果可见, 置P[i, j].dist = newDist;

}

}

2.4 时间复杂度分析

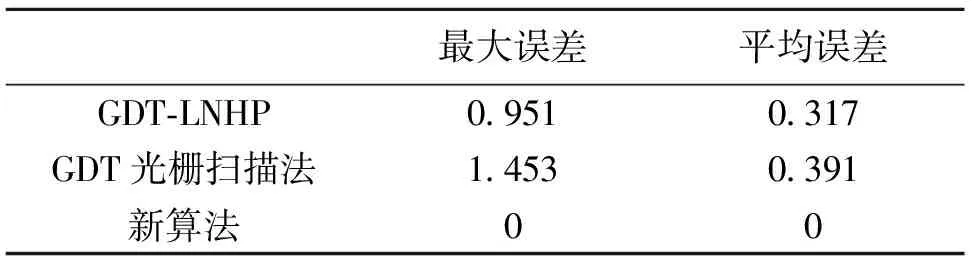
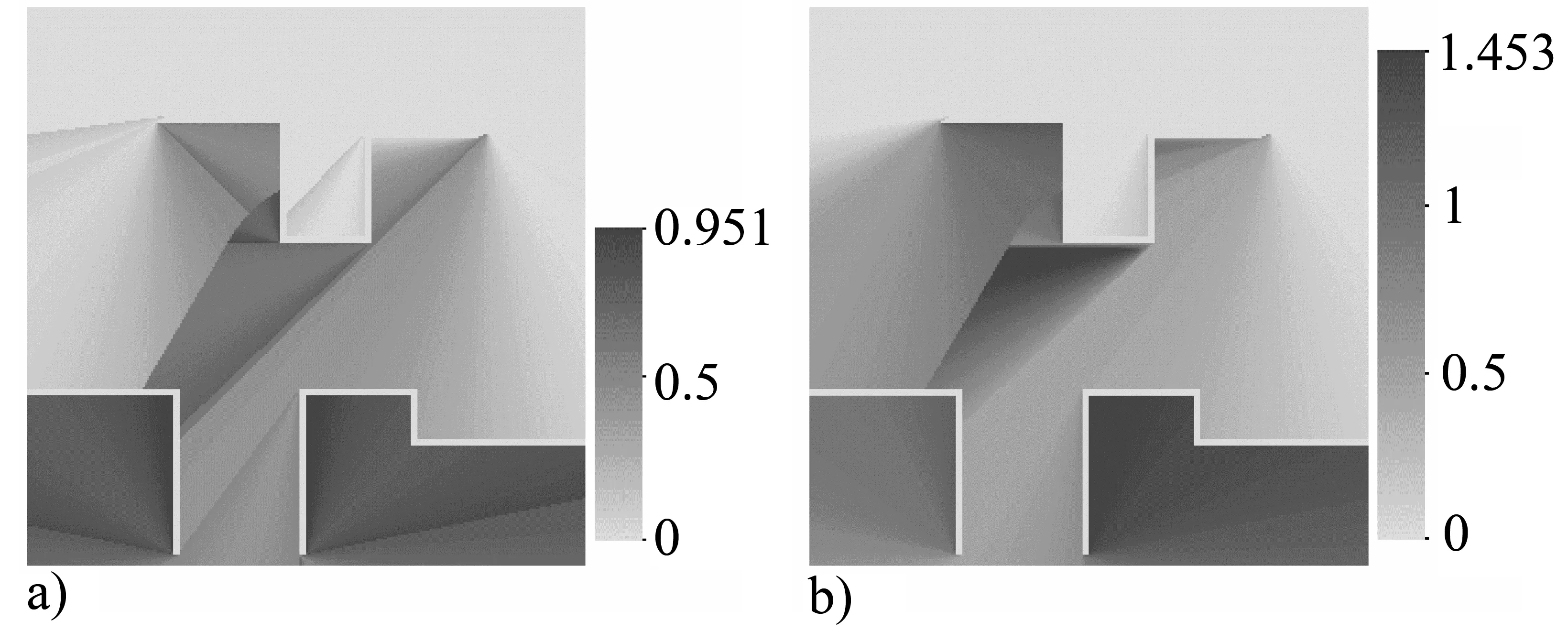
新算法包括三个过程：识别中继源、计算中继源的测地距离、计算背景像元的测地距离。设像元总个数为n，障碍物像元个数为m，中继源个数为k。显然，m<

3 实验结果与分析

采用一幅256*256大小的图像进行了实验。该图像有1个源，3个宽度为3个像元的障碍物。其中，源的坐标为(35, 175)，位于图像右上角。位于图像上半部的障碍物两端均为锯齿状，中部有U形转折。位于图像左下部的障碍物呈直角形状，右下部的障碍物是两个直角的组合物，它们的端点是平直的。

新算法识别了障碍物的20个凸角。其中，上半部、左下部和右下部的障碍物上各有12、3和5个凸角点。图像上的全部障碍物凸角点都被正确识别，没有漏识别和错识别的凸角点。经过解析方法计算比较，各个障碍物凸角点的距离计算误差为0。具体情况见表1所示。

表1 新算法凸角计算准确性

新算法计算的距离图像如图5所示。在图像右上部，等距离线在源附近呈圆环状分布。在图像上部障碍物的两端，分别形成一个环状结构，并在图像左下部汇合。图像左下角和右下角距离值最大。整幅图像的最大距离值为570.131，平均距离值为277.934。

图5 新算法计算的距离图像Fig.5 The distance image by the new algorithm

采用解析方法计算参考距离图，并采用文献[17]中的GDT-LNHP算法和文献[18]中的光栅扫描法进行测地距离变换。其中，GDT-LNHP算法是现有精度最高的测地距离变换算法[17]。将新算法与文献[17-18]算法分别与参考距离图进行比较，统计距离误差，见表2所示。已有算法的平均误差小于0.5个像元，但最大误差都接近或超过1个像元。新算法的最大误差和平均误差均为0。可见，新算法的距离准确性优于已有算法。

表2 GDT-LNHP和光栅扫描法的距离计算误差

文献[17-18]算法的距离误差的空间分布见图6。新算法不存在距离误差。从图6可以看出，文献[17-18]的算法的最大距离误差方向略有差异。其中，文献[18]算法在紧靠障碍物背后位置的距离误差较大。

图6 GDT-LNHP和光栅扫描算法的误差分布Fig.6 Absolute differences for GDT-LNHP and raster scan algorithm

图7 新算法在非凸域内的距离变换Fig.7 Distance transform in a non-convex domain by the new algorithm

此外，还采用新算法在一些复杂非凸域中进行了距离变换实验，部分结果见图7。在图7中，有一个带分岔的开敞空间，其外围是封闭区域。开敞空间为背景区域，封闭区域为障碍物。在开敞空间中的两个分岔附近设一个源，计算开敞空间中各处到源的测地距离。采用新算法计算的最大距离为497.284，平均距离为230.446，如图7(a)所示；将距离值按间距10分段，各距离段的可视化结果如图7(b)所示。从图7(a)看，开敞空间中离源越远的位置的距离越大。从图7(b)看，距离等值线在直线段开敞空间呈较规则的环状分布，在弯曲段和分岔口则呈现为扭曲的环状。该图的距离值与实际相符。

4 结 论

根据上述距离变换研究和实验，可以得到以下结论：① 新算法以障碍物凸角点为中继源，中继源位于最短距离传播路径上，不存在距离偏差，从而避免了中继源设置不当引入的附带误差。② 新算法计算的距离值准确，其距离误差是0个像元。距离值的精度仅与像元的大小有关。③ 新算法的时间复杂度接近于O(n)。其中，线性阶n有一个与障碍物凸角点个数有关的系数。当障碍物凸角点的个数较多时，该系数较大。④ 新算法可应用于二维障碍空间中的距离变换。其距离准确性不受障碍物数量、位置和形状的影响。

参考文献：

[1] ROSENFELD A, PFALTZ J. Sequential operations in digital pictures processing[J]. Journal of the ACM, 1966, 13(4): 471-494.

[2] BORGEFORS G. Distance transformations in digital images[J]. Computer Vision, Graphics and Image Processing, 1986, 34(3): 344-371.

[3] PAGLIERONI D W. A unified distance transform algorithm and architecture[J]. Machine Vision and Applications, 1992, 5(1): 47-55.

[4] SAITO T, TORIWAKI J. New algorithms for euclidean distance transformation of an n-dimensional digitized picture with applications[J]. Pattern Recognition, 1994, 27(11): 1551-1565.

[5] FABBRI R, COSTA L D F, TORELLI J C et al. 2D Euclidean distance transform algorithms: A comparative survey[J]. ACM Computing Surveys,2008,40(1):1-44.

[6] 陈崚.完全欧几里德距离变换的最优算法[J].计算机学报, 1995, 18(8): 611-616.

[7] 王钲旋,李文辉,庞云阶.基于围线追踪的完全欧氏距离变换算法[J].计算机学报, 1998, 21(3): 217-222.

[8] 任勇勇,潘泉,张绍武，等. 基于围线分层扫描的完全欧氏距离变换算法[J]. 中国图像图形学报, 2011, 16(1): 32-36.

[9] LUCET Y. New sequential exact Euclidean distance transform algorithms based on convex analysis [J]. Image and Vision Computing, 2009, 27(2): 37-44.

[10] 徐达丽,任洪娥,徐海涛,等. 基于链码技术的距离变换改进算法[J]. 计算机工程与应用, 2009, 45(25): 176-178.

[11] 陆宗骐,朱煜. 用带形状校正的腐蚀膨胀实现Euclidean距离变换[J]. 中国图像图形学报, 2010, 15(2): 294-300.

[12] GUSTAVSON S, STRAND R. Anti-aliased Euclidean distance transform[J]. Pattern Recognition Letters, 2011, 32(2): 252-257.

[13] 郭仁忠. 空间分析[M]. 武汉测绘科技大学出版社， 2000.

[14] LANTUEJOUL C, MAISONNEUVE F. Geodesic methods in quantitative image analysis[J], Pattern Recognition, 1984, 17(2): 177-187.

[15] PIPER J, GRANUM E. Computing distance transformations in convex and non-convex domains[J]. Pattern Recognition, 1987, 20(6): 599-615.

[16] COEURJOLLY D, MIGUET S, TOUGNE L. 2D and 3D visibility in discrete geometry: an application to discrete geodesic paths[J]. Pattern Recognition Letters, 2004, 25(5): 561-570.

[18] 张青年. 一种顾及障碍物的欧氏距离变换方法[J]. 中山大学学报：自然科学版, 2013, 52(1): 130-135.