高斯激活函数特征值分解修剪技术的D-FNN算法研究*

何正风，张德丰，孙亚民

(1.佛山科学技术学院理学院，广东 佛山 528000； 2.佛山科学技术学院计算机系，广东 佛山 528000； 3.南京理工大学计算机科学与技术学院，江苏 南京 210094)

从神经网络的角度来看，由于神经网络是一个黑箱，不具有明确的物理意义，因此，专家对研究对象的部分知识无法应用到神经网络中。但是，一个模糊神经网络却有明确的物理意义，专家知识很容易结合到模糊神经网络中。因此，模糊神经网络不仅吸取了模糊逻辑和神经网络二者的优点，还克服了各自具有的缺点[1]。正因如此，模糊神经网络成为当前研究的一个热点，并形成了一个较为完善的体系。本文研究的是模糊神经网络混合系统，是模糊逻辑和神经网络一种比较高级的结合方法。在这种系统中，模糊逻辑和神经网络各自发挥自己的功能，利用各自的优势为共同的目标而实现功能结合与互补。

1 动态模糊神经网络的理论分析

1.1 激活函数与隶属函数的选择

一般来说，只要是连续可微的函数都可以作为神经网络的激活函数。在实际应用中，通常取如下S型函数：

(1)

实际上，任何绝对可积的激活函数都能够逼近基于傅里叶级数展开的任意函数。那么，我们要问：非S型激活函数对神经网络的实现和训练有什么影响？由于神经网络的非线性映射能力，在神经网络的实现和训练方面，是否非S型函数能够更好地取代S型激活函数[2]？

为了回答这个问题，我们提出了一个判别函数，该函数由有限个势函数的加权来表示：

(2)

其中，k(x,xi)是x的第i个势函数，ci是实常数，u是势函数个数。这点可以与传统的三层前馈网络的输出进行比较

(3)

实验研究表明：在S型函数、高斯函数与正弦函数之中，正弦激活函数提供最佳映射能力，高斯激活函数次之，S型函数最差。但是激活函数的泛化能力很大程度上依赖于某种映射的局部特性。这种情况下，希望得到一个不仅具有强大的全局映射泛化能力，而且在细化局部方面也有效，并且在已学习的映射上无须太多改动的激活函数。这使得高斯函数激活函数在神经网络的应用方面成为一个不错的选择。由于高斯函数具有各项同性，因此以高斯函数作为激活函数的神经网络称为径向基(RBF)神经网络。

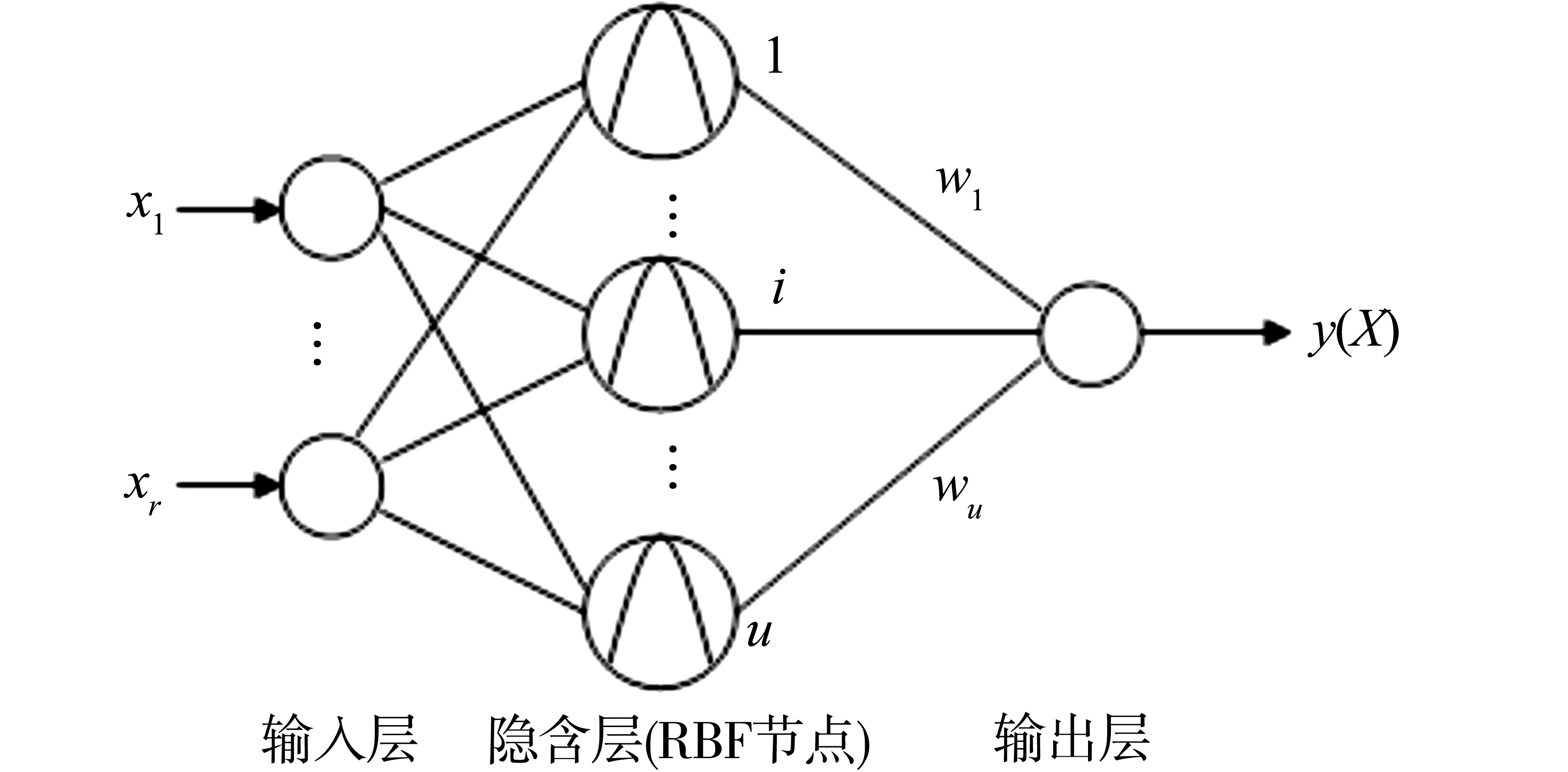
图1 RBF神经网络Fig.1 RBF neural network

一个具有r个输入和一个输出的RBF神经网络如图1所示。该网络可以看成如下形式的映射f:Rr→Rs：

(4)

其中，X∈Rr是输入向量，Ri(·)是基函数，‖ ·‖表示输入空间上的欧氏范数，wi(0≤i≤u)是权值，Ci∈Rr是RBF的中心，u是RBF的单元数。尽管为了定义上的简单，这里仅仅考虑了单输出的情形，但很容易推广到多输出的情形[3]。

如果采用高斯函数而不考虑偏置量，则式(4)可以写为如下的函数：

(5)

如果把各高斯函数的输出归一化，则RBF网络可以产生如下的归一化的输出响应[4]：

y(X)=

(6)

模糊系统提供了一种方法，即把基于专家知识的语言规则转换成自动的控制行为。这种方法明确地提供了一种用数学模型表达不确定性的方式。把隶属的程度定义为隶属函数(MF)，通常该函数是一个位于0到1之间的值。通常来说，两个用的最广泛的隶属描述为三角函数和高斯函数，这两种类型的隶属函数分别如图2、图3所示。

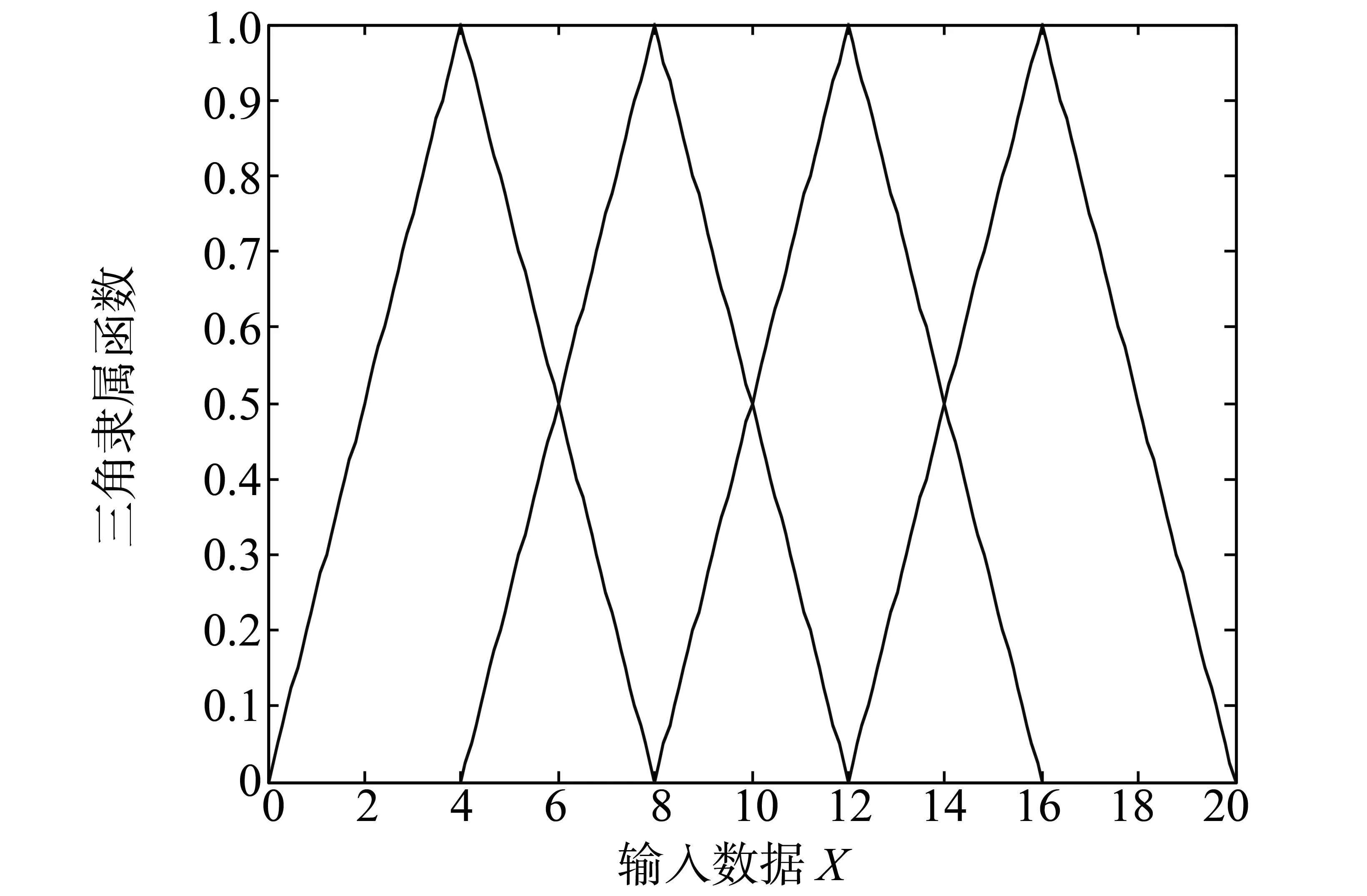
图2 三角隶属函数Fig.2 Triangle MF

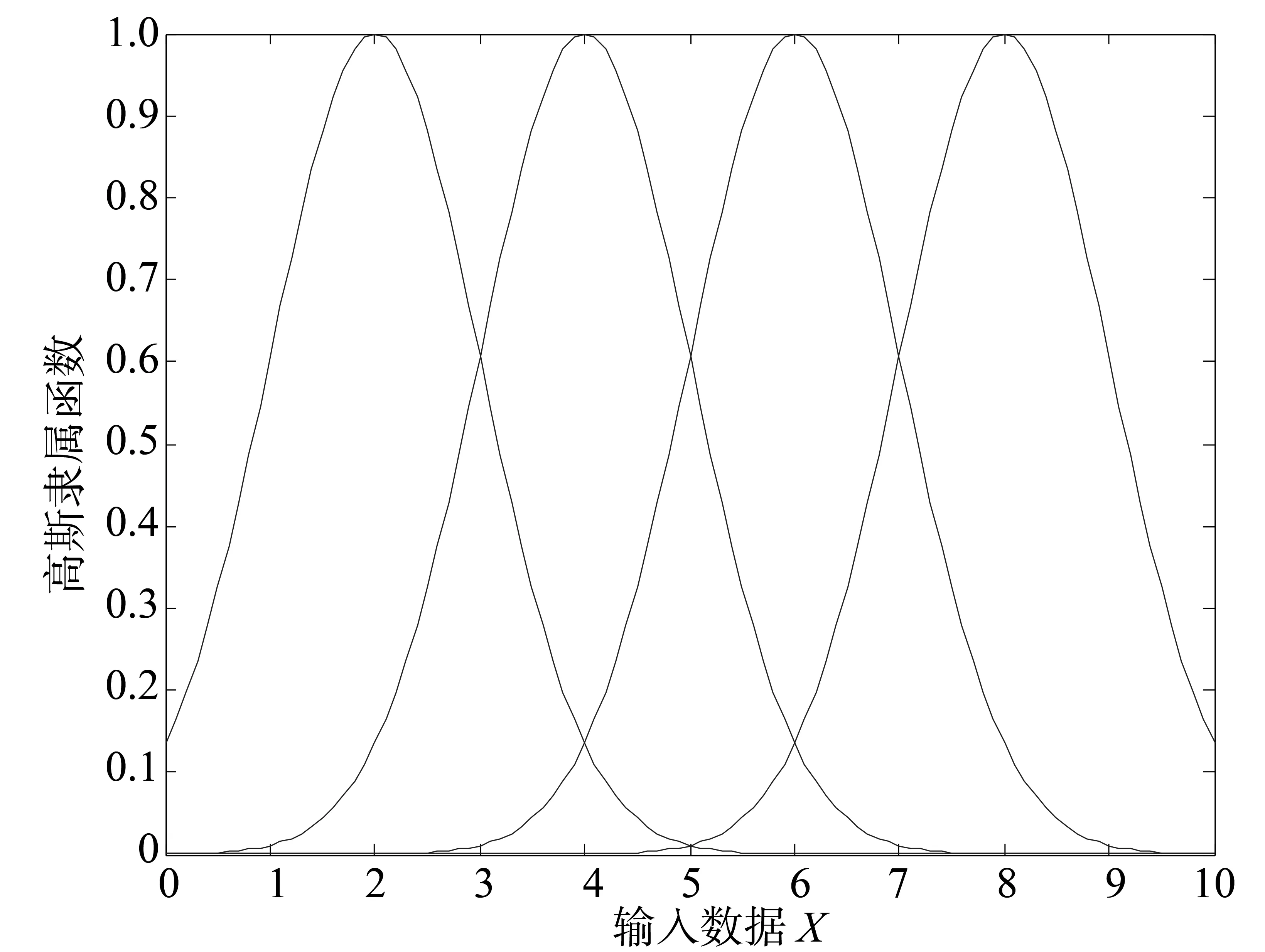
图3 高斯隶属函数Fig.3 Gaussian MF

1.2 动态模糊神经网络的结构

本文提出了一种动态模糊神经网络D-FNN结构及其学习算法，该模糊神经网络的结构基于扩展的径向基神经网络。其学习算法的最大特点是参数的调整和结构的辨识同时进行，且学习速度快，可用于实时建模与控制。

本文所研究的动态模糊神经网络的结构如图4所示，共5层。在图4中，x1,x2,…,xr是输入的语言变量，y是系统的输出，MFij是第i个输入变量的第j个隶属函数，Rj表示第j条模糊规则，Nj是第j个归一化节点，wj是第j个规则的结果参数或者连接权，u指系统总的规则数[5]。

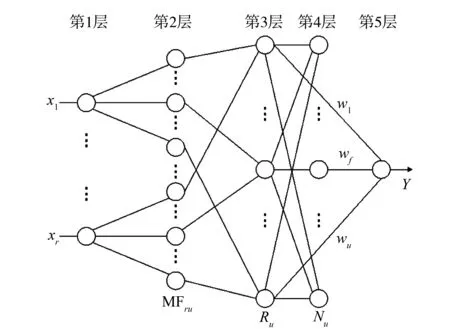
图4 D-FNN的结构Fig.4 D-FNN structure

第1层称为输入层，第2层称为隶属函数层，第3层称为T-范数层，第4层称为归一化层，第5层称为输出层。第5层中的每个节点分别表示一个输出变量，该输出是所有输入信号的叠加：

(7)

其中，y是变量的输出，wk是THEN-部分或者第k个规则的连接权[6]。

1.3 特征值分解(ED)修剪技术

修剪技术对于动态时变非线性系统的辨识是非常必要的。如果在学习进行时，检测到不活跃的模糊规则并加以剔除，则可获得更为紧凑的D-FNN结构。本文采用特征值分解(ED)方法作为一种修剪技术来选择重要的规则。

特征值分解(ED)的目的是为了构建简化的RBF神经网络以及Volterra级数(一种泛函级数)多项式。该方法使用如下的正则方程[7]：

ΦHHθ=ΦHD

(8)

其中，ΦHH=HTH∈Rv×v和ΦHD=HTD∈Rv分别称为相关矩阵和互相关向量。计算ΦHH的特征值分解可以得到：

ΦHH=BΛBT

(9)

其中，Λ=diag(λ1,λ2,…,λv)∈Rv×v为对角矩阵，矩阵的对角元为ΦHH的特征值，同时B=[b1,b2,…,bv]∈Rv×v是正交矩阵，该矩阵的列为相应的特征向量。由于ΦHH是个对称非负矩阵，特征值λ1,λ2,…,λv都是非负实数。因此，该分解可以通过调整使得特征值呈降序排列即λ1≥λ2≥…≥λv≥0。

如果矩阵ΦHH包含零或者接近零的特征值，则表明ΦHH是一个非满秩矩阵，从而可以去掉多余的或者不重要的规则[8]。定义如下测量指数向量IED∈Rv

IED=[IED1,IED2,…,IEDv]T

(10)

其中，Bb=[b1,b2,…,bb]∈Rv×b包含矩阵B的前b列。IED中最大的指数b预示着θ中的应当保留下来的元素位置。同时IED中保留的v-b指数预示着θ应当去掉的元素的位置。

假设得到的b维参数向量定义为θ(b)=[θ1,θ2,…,θb]T， 那么，它可以通过求解简化的正则方程

(11)

ED算法的主要步骤归纳如下[9]：

1) 由式(9)计算ΦHH的特征值分解得到Λ和B。通过检查包含在Λ中的特征值确定保留的模糊规则的规则数。最前面b个最大的特征值的数量预示了应当保留的模糊规则数。

2) 把B分解成B=[Bb,Bv-b]，其中Bb和Bv-b分别对应于B的前b列和后v-b列。

3) 用式(10)计算测量指数向量IED。IED中的最大的b的预示了应当保留的ΦHH的行和列的位置以及ΦHD的行的位置，即规则库的b个最重要规则的位置。

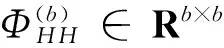
5) 用LLS或者SVD方法求解式(11)得到θ(b)。

2 实验结果与分析

为了验证特征值分解修剪技术的D-FNN算法有效性，我们把本文的算法与其他学习算法进行了比较，并深入探讨了这些算法之间的相互关系。实验表明使用了特征值分解修剪技术的D-FNN具有简洁的结构和优良的性能。

研究人员已经证明一个模糊系统或神经网络是一个通用的逼近器。但是，这只是个存在性结论，并没有给出如何才能找到这样的模糊系统或模糊神经系统[9]。

当一个神经网络用于函数逼近问题时，一般的形式如下：

(12)

其中，wi是权值，Ri(X,wi)是基函数，u是基函数的个数。一旦Ri(X,wi)被选定，权值的选择就可以用线性代数中的标准方法求解。

使用特征值分解修剪技术的D-FNN仿真实验。被逼近的函数为如下的埃尔米特(Hermite)多项式[10]：

(13)

为了学习这个被逼近的函数，使用区间[-4，4]内的随机样本函数来产生200个输入输出数据作为训练集。预先确定的参数如下，且跟文献[11]和文献[12]所选一样。

dmax=2，dmin=0.2，γ=0.977，β=0.9，σ0=2，emax=1.1，emin=0.02，k=1.1，kerr=0.001 5。

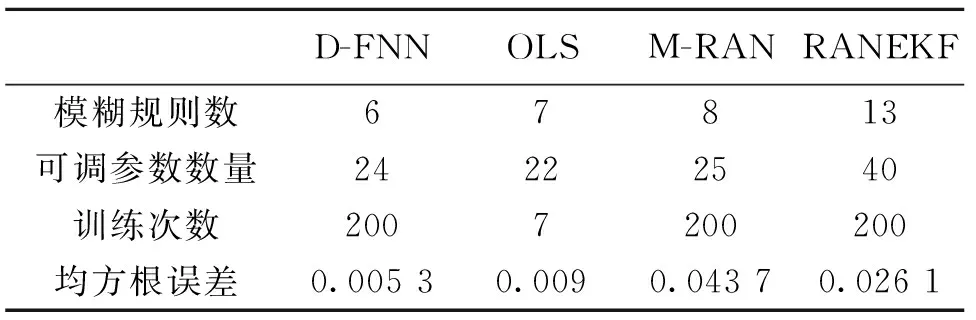
表1 不同算法的结构和性能对比 Table 1 Contrast of the different algorithms in the structure and properties

仿真结果如图5所示。表1列出了用均方根误差估计的结构和性能方面的对比。图5a所示，经过46个训练数据，规则数保持稳定。需要指出，这并不意味着规则是保持不变的。实际上，当新的样本数据加入后，前提参数和结论参数一直保持更新，而且，一条新规则的产生可能会修剪掉已有的规则而同样保持系统的精确。在本例中，当第148个数据达到时，产生了一条新的规则，这时，原来已有的一条规则就显得不重要而被修剪掉。这在规则增长图中是看不出来的，但在题5c中有反映。在这种情况下，产生了一个陡峭的均方根误差。图5b显示训练时实际输出误差。

为了评估D-FNN产生的规则是否合理，由D-FNN产生的规则分布示于图6a中。为了便于比较，画出OLS产生的规则如图6b所示。由D-FNN和OLS(正交最小二乘网络)产生的RBF单元的具体参数列于表2中。

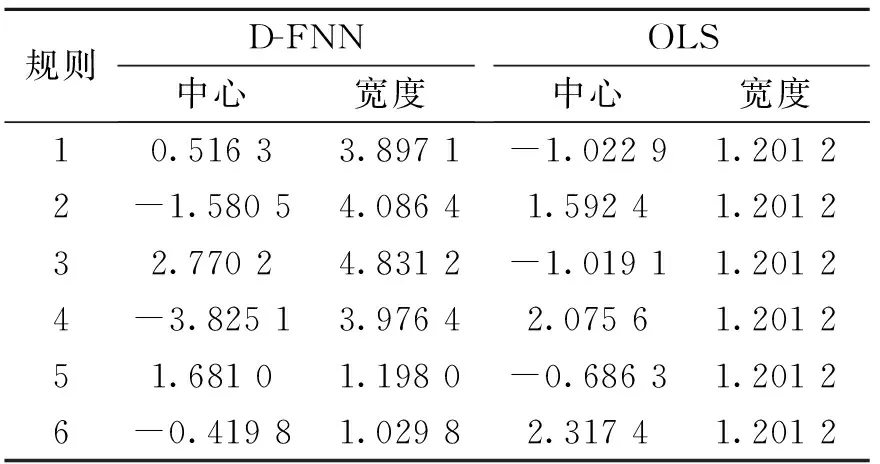
表2 RBF单元的分布 Table 2 RBF unit distribution

由图5d及表2可以看出，由D-FNN产生的规则分布在输出变化大的地方，并根据变化的大小和快慢，以不同的高斯宽度来实现，从而使得可容纳的局部域达到最大。与之不同，OLS方法中，每个RBF的宽度是固定的，当被逼近的函数在不同点出现缓慢不同变化时，基函数的自适应性就差，在变化剧烈的地方，可能会要求有多个RBF产生。如本例中，由OLS产生的RBF节点就有两个非常接近的，即C1=-1.022 9及C3=-1.019 1。所选高斯宽度越小，这个问题越突出。同时，也可以看到，OLS方法确定的规则在整个输入变量空间中并不是均匀分布的，所以，所需规则数多，即使如此，精度还是不如D-FNN高。

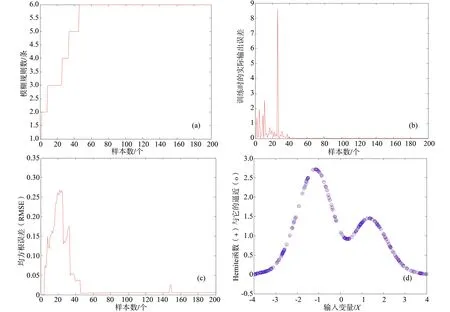
图5 Hermite函数逼近Fig.5 Hermite function approximation

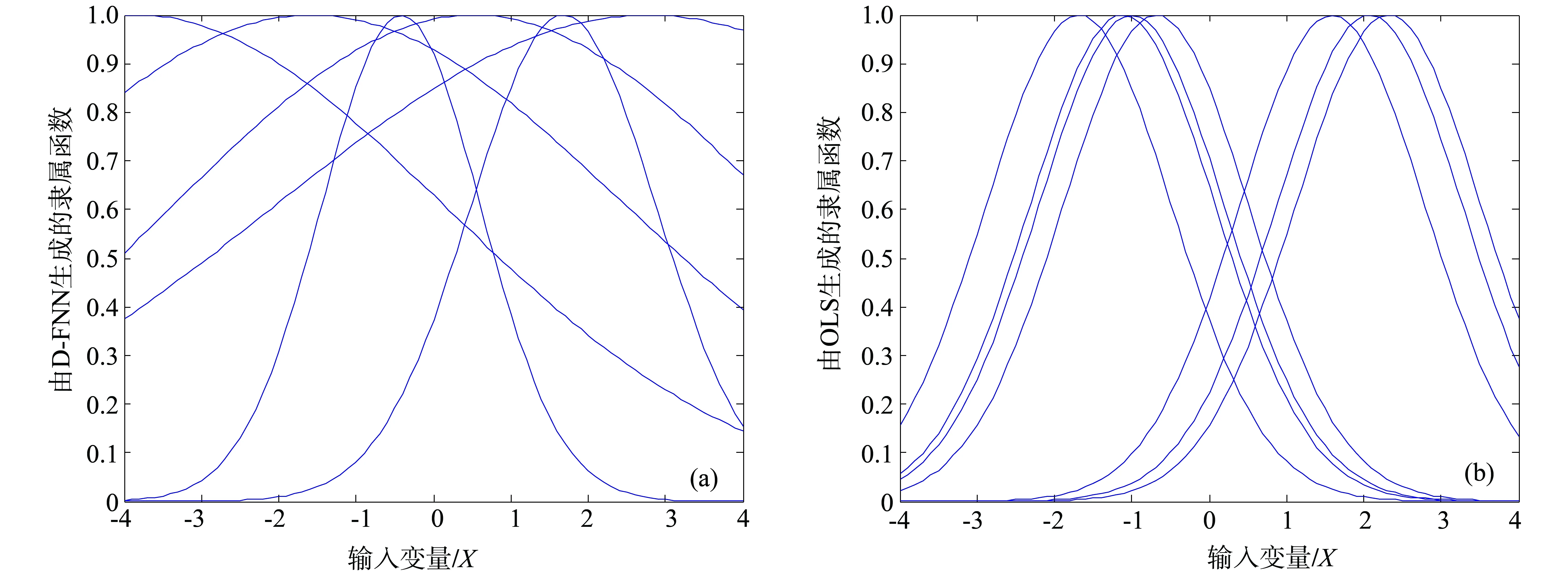
图6 由D-FNN和OLS产生的规则分布对比Fig.6 Produce rules distribution contrast by D-FNN and OLS

3 结 论

修剪技术对于动态时变非线性系统的辨识逼近是非常必要的，在学习进行时，检测到不活跃的模糊规则并加以剔除，所得到的模糊神经网络具有结构小的特点，避免了出现过拟合的现象，因而给使用者带来了很大的方便。实验研究表明选择高斯函数作为激活函数的新算法，不仅具有强大的全局映射泛化能力，而且在细化局部方面也有效。虽然高斯宽度在学习时可以自适应地调整，但学习规则却很简单。仿真结果表明，由于使用了高斯激活函数特征值分解的自适应系统使得D-FNN具有紧凑的系统结构、强大的泛化能力以及快速的学习速度。

参考文献：

[1] CHEN S, COWAN C F N, GRANT P M. Orthogonal least squares algorithm for radial basis function network[J]. IEEE Trans. Neural Networks, 2010, 20(2):302-310.

[2] LEONTARITIS I J, BILLINGS S A. Input-output parametric models for nonlinear systems, Part 1: Deterministic nonlinear systems[J]. Int J Contr, 2009, 41(2): 303-344.

[3] CHELLAPPA R, WILSON C L, SIROHEY S. Human and machine recognition of faces: A survey[J]. Proc IEEE, 2011,93(2): 705-740.

[4] BRUNELLI R, POGGIO T. Face recognition: features versus templates[J]. IEEE Trans Pattern Analysis and Machine Intelligence, 2011, 25(10), 1042-1053.

[5] CHAO C T, CHEN Y J,TENG C C. Simplification of fuzzy neural systems using similarity analysis[J]. IEEE Trans Syst, Man, Cybern, Part B: Cybern, 2009, 35(2):344-354.

[6] WU S Q, ER M J. Dynamic fuzzy neural networks: a novel approach to function approximation[J]. IEEE Trans Syst, Man, Cybern Part B,2000, 30: 358-364.

[7] ER M J. WU S Q. A fast learning algorithm for parsimonious fuzzy neural systems[J]. Fuzzy Sets and Systems, 2002, 126: 337-351.

[8] 马莉, 张德丰, 马子龙. 滑动窗与修剪技术的动态模糊神经网络方法研究[J]. 中山大学学报:自然科学版, 2010, 49(1): 48-52.

[9] Platt J. A resource-allocating network for function interpolation[J]. Neural Computation, 2008, 19(2):213-225.

[10] JANG J-S R. ANFIS: Adaptive-network-based fuzzy inference system[J]. IEEE Trans Syst, Man, Cybern, 1993, 23(3): 665-684.

[11] HONG Z. Algebraic feature extraction of image for recognition[J]. Patt Recog, 2011, 24(2): 211-219.

[12] LU Y, SUNDARARAJAN N, SARATCHANDRAN P. A sequential learning scheme for function approximation by using minimal radial basis function networks[J]. Neural Computation, 2007, 9: 461-478.

[13] KADIRKAMANATHAN V, NIRANJAN M. A function estimation approach to sequential learning with neural networks[J]. Neural Computation,2003, 5:954-975.

[14] 任爱红. 模糊随机过程函数列均方差一致Henstock积分的可积性[J]. 中山大学学报:自然科学版, 2010, 51(4): 41-44.

[15] TURK M A, PENTLAND A P. Eigenfaces for Recognition[J]. Cognitive Neuroscience, 2006, 3(1): 71-86.