计及次近邻原子作用平面正三角晶格振动的色散关系

陈志远，齐文杰，张端明

(1.湖北科技学院核技术与化学生物学院, 湖北 咸宁 437100;2.湖北科技学院电子与信息工程学院, 湖北 咸宁437100;3.华中科技大学物理学院，湖北 武汉430074)

0 引 言

晶格振动色散关系是晶格动力学研究的重要内容之一，国内外固体物理教科书都会涉及，但是，几乎所有的教科书对晶格振动色散关系的讨论，都局限在一维晶格，并且往往只考虑最近邻原子相互作用[1-2]．对于二维或三维晶格振动色散关系的研究并不多见[3-4]，而且增加计及次近邻原子相互作用的讨论更是少见．因此，本研究选择平面正三角晶格为研究对象，利用晶格动力学理论推导了计及次近邻原子作用下晶格振动的色散关系，得到第一布里渊区中三种特殊对称方向的色散关系表达式和曲线，讨论了次近邻原子作用对平面正三角晶格振动色散关系的影响．

1 晶格振动模型与色散关系

1.1 晶格振动模型

(1)

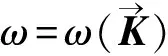
(2)

(3)

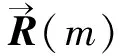
φαβ(0,m)=-γmeα(m)eβ(m)

(4)

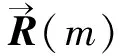
(5)

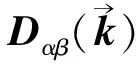
(6)

1.2 色散关系

考虑平面正三角晶格结构如图1所示，任意两个最近邻原子的间距为a，由于正三角晶格结构的特点，这种晶格的每一个原胞中包含有一个原子．将第0号原子的最近邻原子编号为1、2、3、4、5、6，次近邻原子分别编号7、8、9、10、11、12，用γ1和γ2分别表示任意两个最近邻原子间和两个次近邻原子间的弹性力耦合常数．

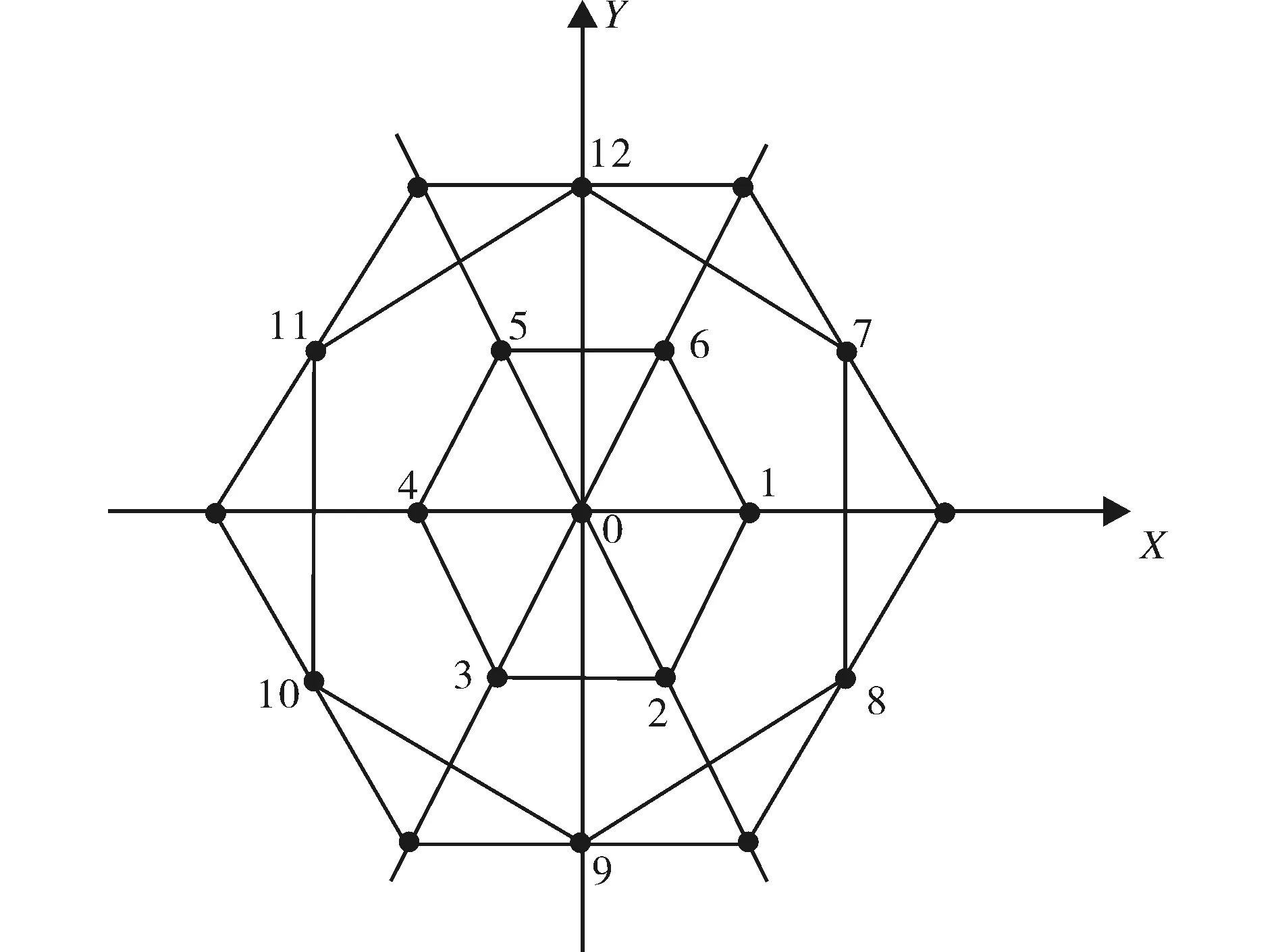
图1 二维平面正三角晶格及其近邻原子的分布 Fig.1 Two-dimensional equilateral trigonal lattice and distributing of neighbor atoms

在图1中建立平面直角坐标系X-O-Y，则从第0号原子至其它12个原子之间的单位向量可以表示为：

由(4)式可以计算出相应的原子之间相互作用力常数φαβ(0,m)如下：

φxx(0,1)=φxx(0,4)=-γ1

φxx(0,2)=φxx(0,3)=φxx(0,5)=φxx(0,6)=-γ1/4

φxy(0,1)=φyx(0,1)=φxy(0,4)=φyx(0,4)=φyy(0,1)=φyy(0,4)=0

φyy(0,2)=φyy(0,3)=φyy(0,5)=φyy(0,6)=-3γ1/4

φxx(0,7)=φxx(0,8)=φxx(0,10)=

φxx(0,11)=-3γ2/4

φxx(0,9)=φxx(0,12)=φxy(0,9)=

φyx(0,9)=φxy(0,12)=φyx(0,12)=0

φxy(0,7)=φxy(0,10)=φyx(0,7)=

φxy(0,8)=φxy(0,11)=φyx(0,8)=

φyy(0,7)=φyy(0,8)=φyy(0,10)=

φyy(0,11)=-γ2/4

φyy(0,9)=φyy(0,12)=-γ2

因为考虑到了次近邻原子的相互作用，所以对0号原子而言将同时受到最近邻和次近邻原子的作用．由(5)式的求和规律，可以得到相应的自身力常数为：

φxx(0,0)=3(γ1+γ2),φxy(0,0)=φyx(0,0)=0,φyy(0,0)=3(γ1+γ2)

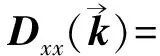
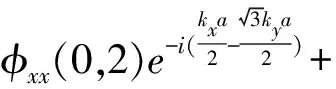
由久期方程(6)式得：

ω2=

(7)

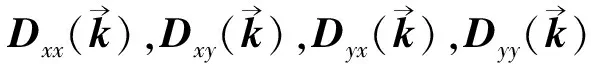
2 分析与讨论

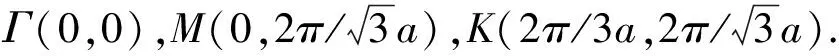
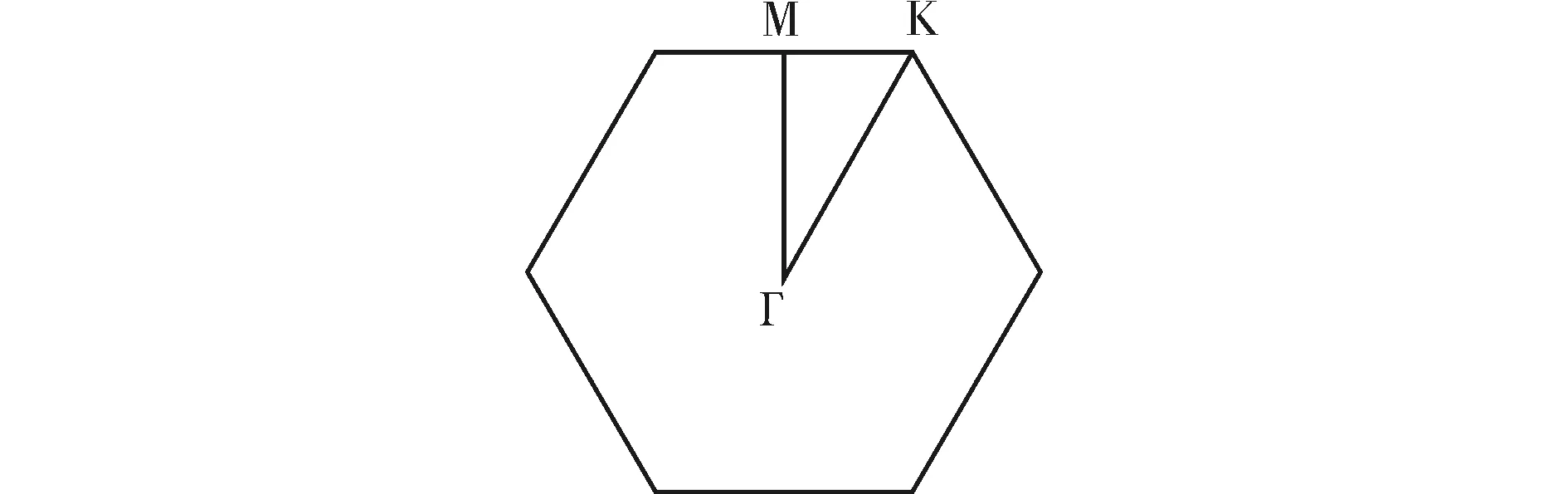
图2 二维平面正三角晶格的第一布里渊区Fig.2 First Brillouin Zone of two-dimensional equilateral trigonal lattice

2.1 第一布里渊区中沿三种特殊对称方向的色散关系

(Ⅰ)沿Γ-M方向上：

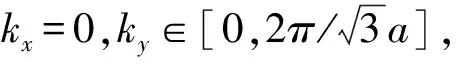
将它们代入(7)式得：

(8)

(9)

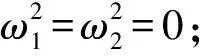
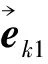
(Ⅱ)沿M-K方向上：

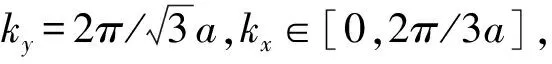
将它们代入(7)式得：

(10)

(11)

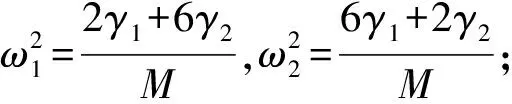
它们与M-K连线方向上每点波矢方向(Γ点与MK线上每点连线方向)既不平行，也不垂直，说明沿M-K线上的格波既非纵波，又非横波．

(Ⅲ )沿Γ-K方向上：

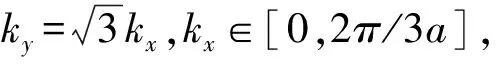
将它们代入(7)式中得到：

(12)

(13)

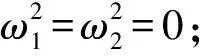
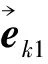
2.2 次近邻原子间作用对第一布里渊区中三种特殊对称方向色散关系的影响

将有关物理量取为无量刚的常数，如原子质量M取单位质量，晶格常数a取单位长度，最近邻原子间以及次近邻原子间相互作用的强弱通过弹性力耦合常数γ1和γ2来描述．我们考虑如下两种情况：当γ1≠0,γ2=0时，即只考虑最近邻原子间作用，不考虑次近邻原子间作用；当γ1≠0,γ2≠0时，即既考虑最近邻原子间作用，又考虑次近邻原子间作用．

若给定γ1=0.8，图3～5分别给出了γ2=0与γ2≠0时第一布里渊区中沿Γ-M、M-K和Γ-K三个特殊对称方向色散曲线．从图3～5中很明显地看出在缺乏次近邻原子作用下晶格振动频谱在Γ点从零开始，两支声学波在M点是非简并的，但是在K点是简并的；最近邻原子间作用足够可以在整个第一布里渊区产生振动频谱．无论γ2=0还是γ2=0.2、0.4、0.6的任意情况，每一个对称方向都存在两条声学支色散曲线，并且纵波频率高于横波频率．

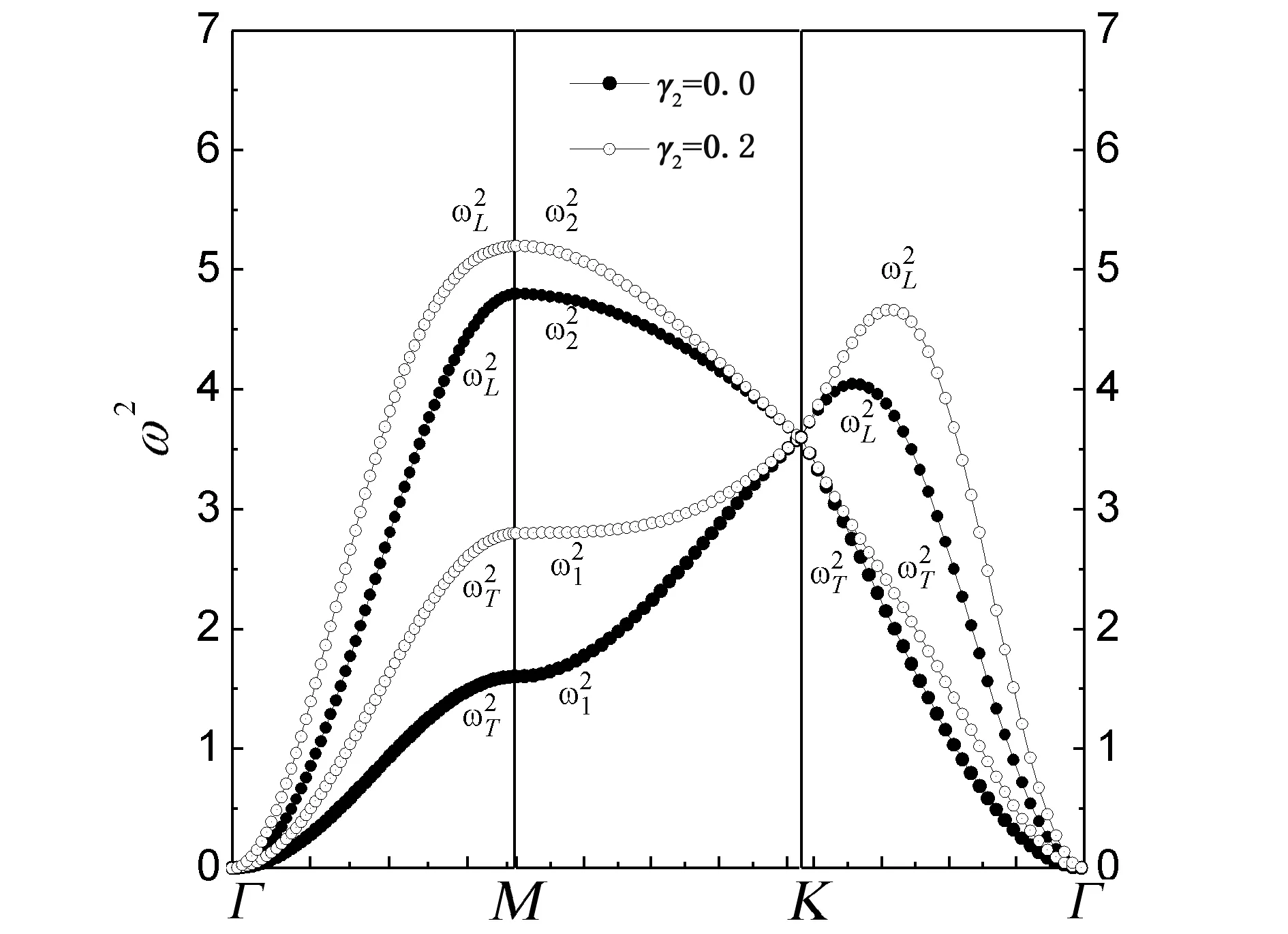
图3 当γ2=0与γ2=0.2时第一布里渊区中三个特殊对称方向色散曲线的比较Fig.3 The comparison of dispersion curves along three symmetry directions in the first Brillouin zone for γ2=0 and γ2=0.2

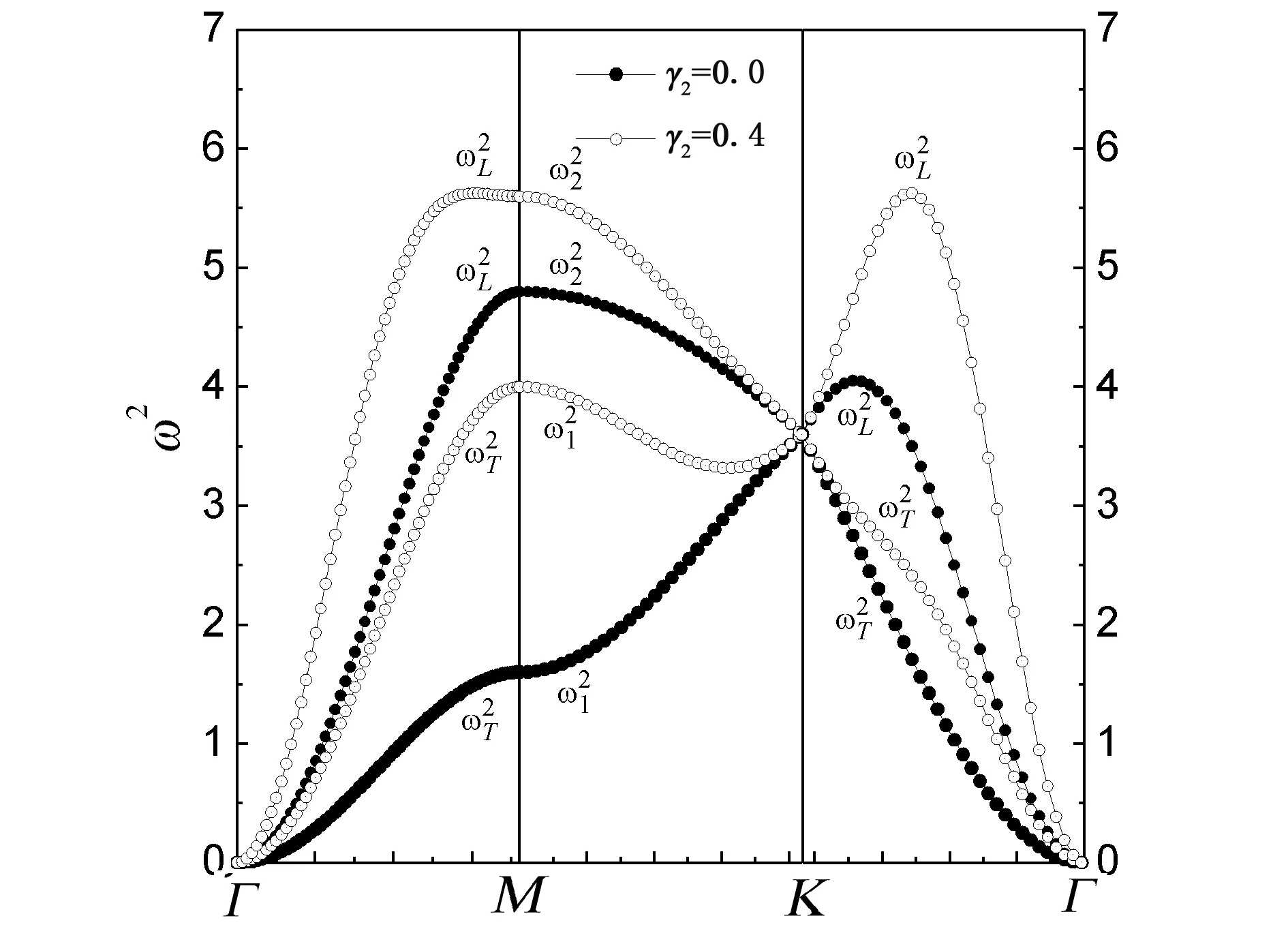
图4 当γ2=0与γ2=0.4时，第一布里渊区中三个特殊对称方向色散曲线的比较Fig.4 The comparison of dispersion curves along three symmetry directions in the first Brillouin zone for γ2=0 and γ2=0.4

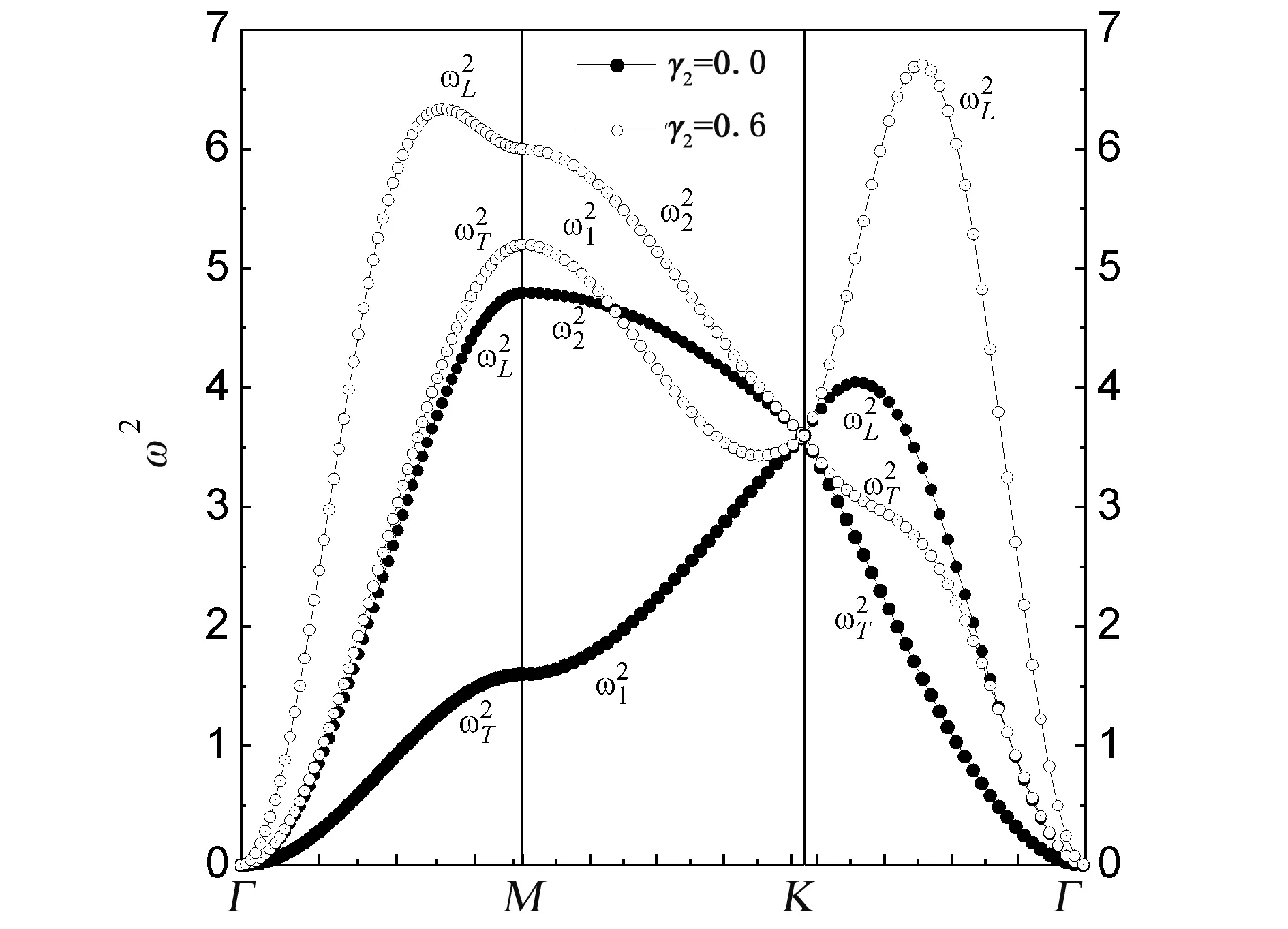
图5 当γ2=0与γ2=0.6时第一布里渊区中三个特殊对称方向色散曲线的比较Fig.5 The comparison of dispersion curves along three symmetry directions in the first Brillouin zone for γ2=0 and γ2=0.6

图3～5也显示，随着次近邻原子间作用的增强，声子频率不断增大(除Γ和K点)，Γ-M方向横波和纵波频率间隙不断减小，并且纵波频率出现极大值；M-K方向两声学波频率间隙也不断减小；Γ-K方向横波色散曲线部分逐渐趋近与最近邻原子作用下的纵波色散曲线重合，而纵波声子频率的极大值显著增大．结果表明，次近邻原子之间的相互作用对三角晶格色散关系影响显著．此外，经过比较发现次近邻原子作用下，声子频率在Γ和K点仍然分别都是简并的，并且其频率大小不受次近邻原子作用的影响，而在M点声子频率亦是非简并的．

3 结 语

本研究利用晶格动力学理论推导了计及次近邻原子作用下平面正三角晶格振动的色散关系，得到第一布里渊区中沿三个特殊对称方向的色散关系表达式；每一对称方向都有两支声学波，其中Γ-M和Γ-K方向有一支纵波和一支横波，而M-K方向两支声学波既非纵波、又非横波，且纵波的频率高于横波的频率．分析讨论了次近邻原子作用对色散关系的影响：在缺乏次近邻原子作用下，最近邻原子间作用足够可以在整个第一布里渊区产生振动频谱；随着次近邻原子间作用的增强，声子频率不断增大，Γ-M和M-K方向两声学支的频率间隙不断减小，Γ-K方向部分横波声子频率逐渐趋近于最近邻原子作用下的纵波声子频率，而其纵波声子频率的极大值显著增大， 表明次近邻原子之间的相互作用对平面正三角晶格色散关系有显著的影响．但是，声子频率在Γ和K点始终不变并分别简并，而在M点频率非简并．

致谢

本工作得到国家自然科学基金委员会和湖北省教育厅提供的资助，在此致以衷心的感谢!

参考文献：

[1] 黄昆,韩汝琦.固体物理[M].北京:高等教育出版社,1988:96-97.

HUANG Kun, HAN Ru-qi. Solid State Physics[M].Beijing: Higher Education Press,1988:96-97. (in chinese)

[2] Kettle C. Introduction of Solid State Physics[M]. 7th ed.New York: John Wiley & Sons inc., 1997:145-150.

[3] 魏建华,解士杰,梅良模.金属卤化物中的晶格振动[J].物理学报,2000,49(10):2027-2032.

WEI Jian-hua, XIE Shi-jie, MEI Liang-mo. The Lattice Vibration of MX Compounds[J].Acta Physica Sinica, 2000, 49(10):2027-2032. (in chinese)

[4] 张祖权.面心和体心立方金属的晶格振动[J].大学物理,1989,8 (10):11-13.

ZHANG Zu-quan. The Lattice Vibration of FCC and BCC Metals[J].College Physics, 1989,8 (10):11-13. (in chinese)

[5] Ashcroft N W, Mermin N D. Solid State Physics[M]. New York: Holt, Rinehart and Winston, 1976:424-440.

[6] Jones W, March N H. Theoretical Solid State Physics[M]. London: John Wiley and Sons,1985:222-223.

[7] 李正中.固体理论[M].北京:高等教育出版社,1985:23-33.

LI Zheng-zhong. Solid State theory[M].Beijing: Higher Education Press,1985:23-33. (in chinese)