基于遗传算法和模糊λ-tau技术对造纸工业清洗系统的行为预测

（1 数学系，印度技术研究所，Roorkee 247667，乌塔拉卡汉德，印度

2 机械与工业工程系，印度技术研究所，Roorkee 247667， 乌塔拉卡汉德，印度

3 应用数学系，ABV-印度信息技术和管理研究所，瓜廖尔，瓜廖尔474010，中央邦，印度）

基于遗传算法和模糊λ-tau技术对造纸工业清洗系统的行为预测

S.P. Sharma1， Dinesh Kumar2， Ajay Kumar3

（1 数学系，印度技术研究所，Roorkee 247667，乌塔拉卡汉德，印度

2 机械与工业工程系，印度技术研究所，Roorkee 247667， 乌塔拉卡汉德，印度

3 应用数学系，ABV-印度信息技术和管理研究所，瓜廖尔，瓜廖尔474010，中央邦，印度）

随着系统结构变得更加复杂，可用性分析成为工业系统设计领域中的一个重要问题。此外，系统的可用性受诸多因素影响，如设计、制造、安装等，所以针对系统的故障行为建模、分析和预测是非常困难的。本文目的是开发一种新的方法，用于计算任何工业系统中的各种性能指标，即可靠性、可用性、MTBF（平均故障间隔时间），ENOF（预期的故障次数），故障率和维修时间。在该方法中，采用遗传算法获得所有组成部件的故障率和维修时间，然后使用模糊λ-tau技术计算各种性能指标。本研究涉及的清洗系统是造纸工业的主要组成部分。运用Petri网络对工作部件之间的相互作用进行建模。使用三角模糊数表示故障率和修复频率，因为他们允许将可靠信息中的专家观点、语言变量、操作条件、不确定性和不精确性纳入系统模型中。基于计算的可靠性参数形成一个结构框架，可帮助维护工程师分析和预测系统行为。

可靠性；MTBF；Petri 网络；语言变量；遗传算法；最优化

1．介绍

随着工业系统的复杂性与日俱增，系统分析员的工作变得更具挑战性，需要研究、表征、测量和分析系统行为的不确定性。他们运用各种技术，而这些技术需要组件故障和维修的模式。但不幸的是，过去记录提供的数据是不完整、不精确、模糊和相互矛盾的，这导致了基本故障事件的信息缺乏。此外，使用年限、不利工作条件和各种变化，对系统各单元的影响不同[1]。因此，为系统建造一个准确和完整的数学模型是很困难的。为解决可靠性评估中的不确定性问题，概率和非概率技术得到使用。由于对系统复杂性的不精确和人类判断的模糊性[2]，概率法和模糊方法处理不确定性问题，在本质上是随机的。

模糊方法可以处理与系统性能相关的不精确和不确定信息，是比传统方法如Bayesian统计法[3]更好、更一致、更精确有效的方法。这些方法经常使用模糊集、可能性理论和语言变量，目前仍处于发展阶段。Singer[4]开发了一种新的方法，利用模糊集方法和故障树找出各种可靠性参数，使用三角模糊数来代表故障率和维修时间。Chen 和Mon[5]采用置信区间来分析模糊系统可靠性。通过理论分析和计算机模拟结果，已经表明相对Singer的方法，他们提出的方法更具普遍性且更直接。Chen[6]提出了一种新的方法，通过使用模糊数算术运算来分析模糊系统的可靠性。Knezevic和Odoom[7]通过利用Petri网（PNs）代替故障树，提出了模糊λ-tau 方法，能够更有效地提供可靠性指数。该方法中模糊集理论被用于代表故障和修复数据。Wang等人[8]提出一种方法，使用模糊模式可以在连续的工作范围内构造故障次数。该方法可以很容易地模拟可修复和不可修复的事故，并能识别系统修复后的再次故障。通过191辆汽车发动机的不同维修时间的验证，该方法已经得到证明。Yadav等[9]提出了一个机制用于收集不准确的信息和知识，并将它应用于可靠性改进预估。这个推荐方法已经被一个案例证明。Jiang和Chen[10]建立了具有模糊可靠度的系统的可靠性分析基础，铁路系统的一种传感器的模糊可靠性分析的案例验证了该算法的逻辑性。计算结果表明，该算法符合工程经验。Tanrioven等人[11]采用具有Markov模型的模糊逻辑来描述转换率和基于季节变化的温度，可识别多种气候条件。一个电力系统的例子也已经证明了该方法的有效性。通过运用模糊仿真和评估系统性能，Zhao和Liu[12]研究了预期系统寿命、系统寿命和系统可靠性，提出了多级系统和网络系统的一些数值实验。Huang等人[13]提出了一种新的方法，采用模糊算法、人工神经网络和遗传算法来确定评估参数的隶属度函数和多种参数寿命分布的可靠性函数。该方法的有效性已经被正态分布和威布尔分布举例证明。对于如何解决不确定/不精确参数的间隔优化问题，Rao等人[14]结合在印度加压重水反应堆安全系统应用的实例，提出了模糊-遗传方法。Ke等人[15]提出了一种方法用于构建系统特征的隶属函数，该方法假设操作和备用机组的失败次数和修复次数符合模糊指数分布，数值算例说明了该方法的实用性。W ang 和 Watada[16]使用模糊随机变量研究了一个串并联系统的冗余分配问题，数值算例可说明该方法的可行性，并量化其有效性。使用传统的λ-tau方法和遗传算法，Komal等[17]提出了一种基于λ-tau技术的遗传算法（GABLT），将该方法在造纸工业中应用洗涤装置，并给出改善系统性能的建议。Taheri和Zarei[18]研究了在模糊环境下Bayesian系统的可靠性。模型参数被假定为具有模糊先验分布的随机变量，并且已经计算出系统可靠性的模糊Bayesian评估值，一些案例验证了该方法的有效性。Kumar等人[19]采用实数编码遗传算法和模糊λ-tau方法对垃圾清理机器人的可靠性进行了分析。该方法可计算出各种可靠性参数，并做了各种故障发生概率的灵敏性分析。

除了修复系统的可靠性，模糊方法被广泛用于研究人的可靠性和探寻影响人可靠性的因素的相对重要性[7,20]。Bertolini[21]分析人的可靠性和使用模糊分类系统计算错误行为的概率。Li等人[22]开发了一种新的模糊人为错误的风险评估方法，用于确定人为错误风险的重要性。采用模糊逻辑来实现该模型，并有一个例子被用来证明该方法。结果表明，该方法比传统的方法更现实，而且是可行的和有价值的。

在不精确推理方法中，模糊方法（FM）作为最可行和最有效的工具之一。另一方面遗传算法（GA），作为启发式技术的成员，也是一个功能强大的工具，并多次运用于可靠性/可用性优化。当搜索的解空间相对较大、嘈杂和非线性时，GA能更好地运用。Hsieh等人[23]运用遗传算法，解决了多种可靠性设计问题，如串联系统、串并联系统和复杂系统的可靠性最优化。Jeang[24]提出，计算机辅助模拟软件将提供可靠性优化设计。已经开发了许多方法，并已被用于可靠性设计。但是，对于可靠性设计和优化已有的文献尚没有建立一种精确、科学的方法。考虑到最大的系统可靠性和最小的总成本，运用多个模糊目标规划，Li[25]解决了相关问题。Ram irez-Marquez和Coit[26]提出了一种新的启发式方法解决多阶段串并联系统的冗余分配问题。Yalaoui和Chatelet[27]针对串并联系统的可靠性分布问题，制定了一个逼近函数。针对串并联冗余的可靠性问题，You和Chen[28]提出了一种高效的启发式方法。Liu等人[29]为电力系统可靠性评估提出了一种新的状态选择技术。采用概率降序顺序，通过最小数目的计算和比较，已经推导出的快速排序算法（FSA）迅速选择系统状态要求的数目。动态地选择和分析系统状态直到满足指定的精度。Juang等[30]提出了一种新的基于遗传算法的方法，用于计算最优的MTBF，M TTR值。开发一个基于理论的互动性决策支持系统，用于在可修复的串并联系统的完整设计过程中帮助设计师建立和存储元件参数。Azaron等[31]利用遗传算法来解决不同单位不可修复的冷备用冗余系统的多目标离散可靠性优化问题。其结果与离散时间近似计算法得出的结果相比较，用来显示遗传算法的有效性。基于组件区间值可靠性的随机优化问题，Bhunia等[32]将优化问题可靠性作为机会约束公式，并通过实数编码遗传算法解决问题。通过灵敏度分析，已经分析了该方法的稳定性。通过使用多目标遗传算法与离散事件模拟，Lins和Droguett[33]解决了冗余分配问题，属于不完善的维修。通过具有分析解决方案实例，验证多目标GA，当和多目标蚁群算法相比，显示了其卓越的性能。

本文目的是设计一种方法来判断任何修复系统的性能测试结果。该设计方法是结合GA和模糊λ-tau方法，它可以描述为以下阶段：（i）为所选系统开发一个优化模型；（ii）利用GAs获得设计阶段的造纸工业清洗系统的各个组成部分的MTBF和MTTR，并优化可用性参数。可用性和GA程序的优化模型，确保可以获得系统可用性的成本效益参数，这将帮助系统分析员设计出最佳的设计政策和维修政策。（iii）使用模糊λ-tau方法来计算各种性能测试结果，如M TBF、可靠性、可用性、ENOF等等，Petri网（PN）是一个功能强大的工具，由于系统的动态建模能力，它被广泛地用在复杂制造系统和程序的建模和分析中。Petri网采用图形描述情况和事件的因果关系。PN有静态和动态部分。静态部分包括三个对象：地方，过渡和箭头，而动态部分只包含符号[34]。Desrochers和Al-Jaar[35]，Baccelli等[36]和Liu、Chiou等人[37]证明Petri网的故障树分析（FTA）和马尔可夫链模型的优越性。Adamyan和He[38,39]分析可知Petri网模型提供了评估质量的能力和对计划外故障和故障的顺序的可靠性影响。基于一些触发条件，Petri网有跟踪系统的状态和在这些状态间转换的能力。而这种能力允许结合故障模式进行分析，并预测其潜在的严重程度，以及估计故障模式发生的概率。这点来看，清洗系统的工作单位之间的相互作用是基于Petri网建模。用矩阵方法[37]，得到不同的割集。这样得到的结果，可以帮助系统设计人员制定最佳的设计和保养原则。

2．方法

解决方法分为两个阶段。在第一阶段中，使用GA获得最优M TBF和MTTR，在第二阶段使用中使用模糊λ-tau方法，获得各种可靠性参数。两个阶段的方法的流程图如图1所示，阶段描述如下：

2.1 第一阶段，形成推荐系统的优化模型

上文所述，从过去记录的信息来看，获得的信息依赖于系统的配置/结构，所以正确分析系统的行为是非常困难的。因此，为了找出成本有效方式（最佳值）的可用性参数，使用系统可用性优化模型和GA。阶段描述如以下步骤：

2.1.1 列出系统可用性的近似表达式

获得串并联系统的可用性表达式，先得假设：（i）组件是独立运行的，即组件的故障和修复特性在统计上是独立的；（ii）故障率λi和修复率μi是常数；（iii）λi《μi；（iv）为每个组件提供独立的维修设施。给定的工业系统被划分为其组成成分，并根据可靠性框图（RBD），可获得可用性、故障率和修复率的表达式[40]。

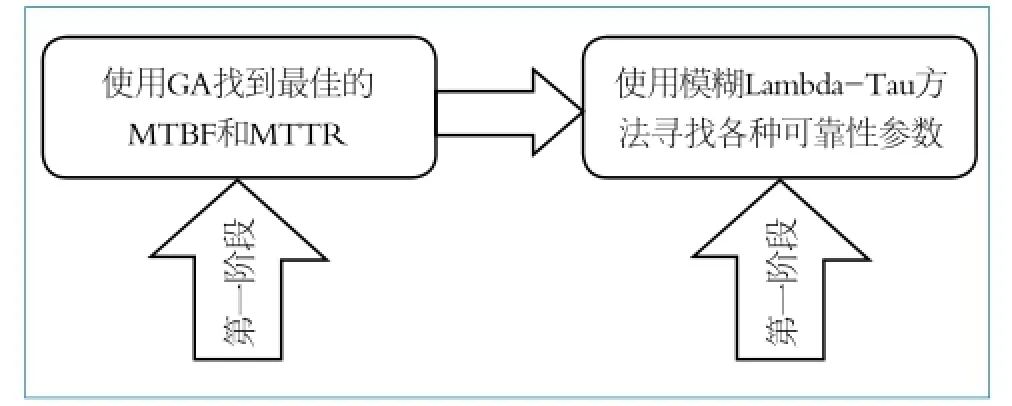
图1 推荐方法的流程图

串联和并联系统的基本参数如表1所示。基于表1中的表达式，系统中的近似可用性表达式可以写为：

2.1.2 列出系统总成本表达式

制造成本取决于产品规格。如果任何组件的MTBF较长，故障率将是较低的，表示该组件是高度可靠的，从而导致制造成本的急剧增加[25]。组件的MTBF和制造成本是彼此相关的，数学关系式可表示为[41]：

其中， CM TBFi和M TBFi分别代表第i个组件的制造成本和平均故障间隔时间（MTBF），而αi，βi和χi为常数，表示的第i个组件的物理性质，βi＞1。关系如说明图2(a)。

运行过程中，系统组件相互作用。任一组件的故障可能会导致其他故障或损害整个系统的效率。为了保证系统的运行，必须尽快修复故障组件。因此需要经验丰富的工作人员按时修复故障组件。在这种情况下，尽管维修时间短，巨大的设备投资导致较高的维修成本。假设M TTR和组件的维修成本具有线性关系，较低的MTTR表示较高的维修成本，数学关系可表示为[30]：

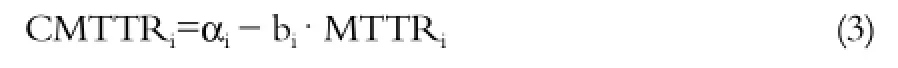
其中，CMTTR i和MTTRi分别表示组件第i个组件的维修成本和MTTR，其中，ai和bi是常数。关系如图2(b)所示。根据公式(2)及(3)，总成本可以写为：

2.1.3 构建目标函数

2.1.4 MTBF和MTTR的上限和下限

2.1.4 对模型求解

结合步骤（2.1.3）和（2.1.4）中的公式，形成一个优化模型。使用GA对该模型求解。GA程序的流程图如图3所示。GA求解过程可以简单地写成：

（i）生成随机初始对象总体。

（ii）评估总体中的每一个对象的适应度。

（iii）重复。

（a）选择最佳排名个体，对其进行重复生产。

（b）通过交叉和变异（遗传操作），重新生成新的一代，并繁衍后代。

（c）评价的后代个体的适应度。

（d）替换最差排名人口的后代。

表1 并串联系统可用性的基本参数

（iv）重复，直到满足终止条件。一旦获得最佳的M TBF，M TTR值，开始第二阶段。

图2 (a) MTBF和制造成本；(b) MTTR和维修成本之间的关系。

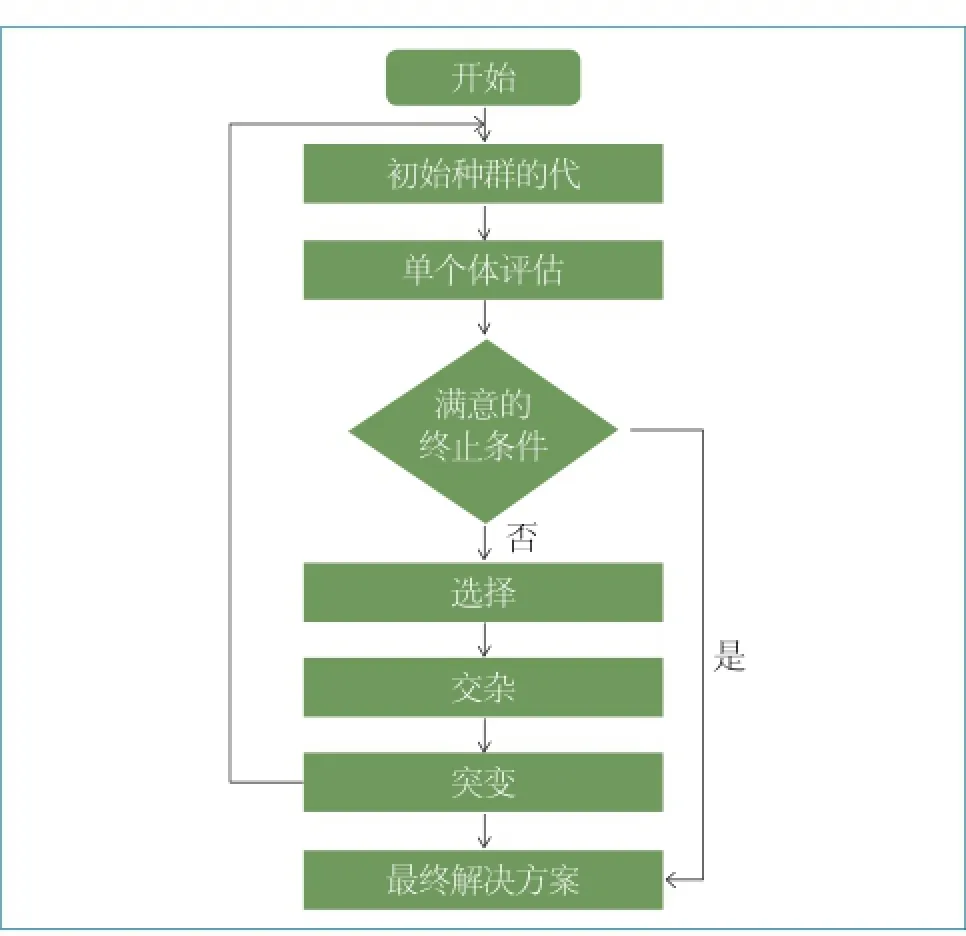
图3 GA流程图

2.2 第二阶段：采用模糊λ-tau方法，计算各种可靠性参数

在这个阶段，采用模糊λ-Tau方法，前阶段获得的最佳MTBF和MTTR值被用于计算各种可靠性参数，如模糊故障率，维修时间，可靠性，可用性，ENOF和平均无故障时间。提高了该方法的效率。模糊λ-tau方法的过程步骤可描述如下：

2.2.1 收集所有组件的故障和维修数据

在这个步骤中，历史/当前记录系统收集了所有与组件的故障率ki和维修时间Si相关的数据。在本研究中，利用第2.1阶段提出的技术，获得了有关故障率和维修时间的数据。

2.2.2 计算PN模型顶部的模糊数据

为了处理数据的模糊性和不确定性，所有组件的精确数据（λi和τi）被转换成三角形模糊数据（和），± 15%扩展范围（±25%，±50%扩展范围，如图4）。其中，是模糊故障率和是模糊维修时间。其中组分i，和j=1，2，3，分别作为三角形的隶属函数的下限、平均值（精确值）和上限值。

2.2.2.1 和转换的表达式

2.2.2.2 或转换的表达式

2.2.3 计算各种可靠性参数

只要每个组件的故障率和维修时间的三角模糊数输入值是已知的，精确故障率和维修时间的相应模糊值（和可以通过公式(7)-(10)获得。为了定量分析系统行为，可以通过图形获得和显示各种可靠性参数左右扩展值。

表3中列出了表达式。

2.2.4 找出所有计算参数的模糊化值

图4 三角模糊数输入值

表2 模糊λ-τ方法的基本表达式

表3 一些可靠性参数

由于大部分由人类或机器执行的行动或决定是二进制或精确的，所以将模糊输出值转换为一个精确值是必要的。模糊输出转换成精确值的过程被称为反模糊化。文献中介绍了许多反模糊化技术，如最大隶属原则，中心区（COA），求和中心，最大面积中心等[43]，根据不同的应用进行选择。本次研究选用COA方法，因为它与平均数据是等价的，它非常适合可靠性计算方法。如果模糊集合的输出值的隶属函数 μ( x ) 被描述在区间[x1，x2]内，那么COA去模糊可以被定义为：

3．实例

选择一个造纸厂来证明该方法。选择位于印度北部，每天生产180吨纸的造纸厂，运用提出的技术讨论其故障行为。造纸厂有许多功能单位，如进料、纸浆准备、洗浆、筛选、漂白和纸张准备。本此研究洗涤系统，包括以下组成部分：

（a）滤波器[SF]：它被用来从煮浆中排出黑色液体。一个单元是用于清洗系统的正常工作。

（b）除垢器[SC]：三个单元并联排列。该子系统通过离心作用来清洁纸浆。任一单元故障都将降低系统的运行效率，以及纸张质量。

（c）筛选装置[SS]：串联布置两个单元。通过过滤作用，用于去除过大，未煮过的和异形纤维纸浆。任何一个单元的故障将导致系统故障。

（d）脱水机[SD]：两个单元并联排列。脱水机的功能是减少纸浆的黑度。当两个组件都失效时，脱水机将完全处于故障状态。

图5 清洗系统的RBD模型

图5中RBD显示了清洗系统中各单元之间的相互作用。

基于RBD和表1中给出的表达式，给出系统的优化模型。

其中

目前的工作是基于计算清洗系统第2.1节的M TBF和MTTR最佳值，和系统（2.2）的各种模糊可靠性参数。从系统以前的历史收集到MTBF方差范围、制造成本、MTTR和维修成本，并分别如表4和表5所示。GA参数，即人口规模，交叉率和变异率，分别为80%、0.8和0.05。终止准则已被设置为最大数目4000代或运算的相对误差等于10-6。两者取其先。该程序运行了25次，并采用最佳人选。按照第2.1节中描述的步骤进行，并遵守第2节中的附加条件，表6中列出了优化设计参数计算值。该方案的一个执行过程所用时间为401s。

一旦获得M TBF和M TTR的最佳值，开始第二阶段（2.2）。使用Petri网，该系统的工作状态之间的相互作用如图6所示。最小割集为{SF}，{SC1，SC2，SC3}，{SS1}，{SS2}和{SD1，SD2}，使用矩阵方法可以得到。为了提高模糊λ-tau方法的效率，第一阶段（2.1）获得M TBF和M TTR最佳值，用于第二阶段（2.2）计算中，如表6所示。利用模糊λ-tau方法，获得各种模糊可靠性参数和不同扩展范围的反模糊化值，分别如图7和图8所示。表7介绍了解模糊值。

4．结果与讨论

可修复的串并联系统的设计是低效的，如果仅仅依靠经验方法，它往往由于继承设计经验的困难性而导致设计成本增加。应用软计算技术，如遗传算法，可修复的串并联系统的分析和优化设计问题，在促进决策系统参数设计方面是非常有用的。从一点来看，使用系统可用性和设计约束的优化模型，远离了变化莫测的系统。获得每个组件的MTBF和MTTR最优值（如表6），并将其应用到各种可靠性参数的计算中，使得模糊λ-tau技术的效率可能会增加。从表6中，明显看出每个组件的M TBF和M TTR的最优值在范围内，详细说明如表4和表5。

表4 MTBF的变换范围和组件的制造成本

表5 MTTR的变化范围和组件的维修成本

表6 参数的最优化设计

图6 洗涤系统的Petri网模型

目标函数的优化值是7.0912×10-8。

模糊可靠性参数总结如图7，每个置信区间（a-水平），范围从0到1，增量为0.1，左右偏差。根据a值，分析师预测系统的措施。图形化的结果（图7）表明，如果使用平均三角模糊数描述输入数据中的不确定性，那么故障率和维修时间的可能性分布是扭曲的三角形，因为运用模糊操作后，三角形的直边变成了抛物线。计算和描述了各种可靠性参数的精确值和反模糊化值误差范围±15%，±25%，±50%，如表7所示，图形方式见图8，这清楚地表明，各种可靠性参数的反模糊化值随着误差变化而改变。表和图还表明故障率，修复时间和预期的故障数的去模糊值，随着误差增加而增加。另一方面，故障、可靠性和可用性的平均时间反模糊化值随着误差增加而减少。这意味着，通过模糊方法得到的值本质上是保守的，从性能维护方面，这可能是有益于维护工程师进行维护的。因此，从上面的分析很清楚得到，维护应根据反模糊化MTBF而非精确MTBF，因为通过反模糊化值M TBF，可以建立维护时间之间的安全间隔，并可在系统达到精确值之前，对系统内各项设备的条件或状态进行检查。因此，在选择模糊输入数据的精确值的误差范围时，一定要对系统有全面的了解，熟悉系统的现有的数据和操作环境。

图7 ±15%、±25%和±50%误差下的各种模糊可靠性参数

5．管理的影响

在系统可靠性分析领域，分析师经常需要使用主观判断，由于系统依存性导致不确定数据和近似系统模型，其结果取决于分析师/专家的判断以及从不同来源收集到的信息的质量。此外，可靠性建模中，要非常细心地处理数据，以确保输入的数据和提出的方法质量好，否则结果有偏颇。保持逻辑性观点，工作人员对量化模糊和不精确性的判断的有效性，研究成功采用统一的方法（定性和定量）进行评价和评估系统故障行为。各种可靠性参数的估计通常能帮助维修管理者理解系统的动态行为。根据置信区间值（a），分析师可以预测系统的可靠性测量结果，并能采取必要的步骤以提高系统的性能。该方法将帮助管理人员：（i）进行设计修改，如有需要，以达到最小的故障，及（ii）有利于制定维护（维修和更换）决策。

图8 各种可靠性参数的精确值和模糊值，A：精确值，B、C和D：分别扩展±15%, ±25% 和 ±50%

6．结论

由于工业系统的复杂性不断增长，如果基于经验方法分析进行分析，可修复的串并联系统的设计是不够的。此外，该系统的设计成本会增加，因为基于经验分析系统行为是非常困难的。应用软计算技术，如GA来分析和优化可修复串并联系统的设计问题，应该对系统参数设计的决策是非常有用的。本研究给出一种新的方法来计算各种性能测量结果，并且基于计算的可靠性参数，开发了结构框架，可能有助于维护工程师分析和预测系统行为和每个组件的相关特性。由于系统配置的复杂性，从历史纪录中获得的数据，是不精确和不准确的。鉴于这一事实，在本文2.1节已尝试使用GA来区分数据，在第2.2节，模糊λ-tau方法的效率可能会增加。使用具有系统可用性和设计限制的最佳化模型来计算清洗系统的MTBF和MTTR的最佳值。已尝试对与清洁系统性能相关的不精确、不确定的依赖信息进行处理。已观察到的Petri网作为一种有价值的工具，用于模拟离散动态系统，并研究他们的行为。图示法帮助决策者理解系统不同组成部分之间的相互作用。计算各种可靠性参数，这可能有助于有关管理者计划和调整适当的维修习惯/策略来提升系统性能，从而降低运营和维护成本。因此，这将有助于管理重新分配资源、维修决策，实现系统长期运行可用性，提高造纸行业的整体生产力。除了这些优点，系统性能分析可用于进行成本效益分析、业务能力研究、库存/备件管理系统和更换决定。

表7 在不同扩展范围内的精确值和反模糊化值

（丁宇/编译）

[1] R.K.Sharma, D.Kumar, P.Kumar, Predicting uncertain behavior of industrial system using FM:a practical case, Appl.SoftComput.8 (1) (2008) 96-109.

[2] A.K.Verma, A.Srividya, R.S.P.Gaonkar, Fuzzy-Reliability Engineering, Concepts and Applications, Narosa Publishing House Pvt.Ltd.,New Delhi, India,2007.

[3] K.Y.Cai,System failure engineering and fuzzy methodology: an introductory overview, Fuzzy Sets Syst.83 (1996) 113-133.

[4] D.Singer, A fuzzy set approach to fault tree and reliability analysis, Fuzzy Sets Syst.34 (2)(1990) 145-155.

[5] C.H.Cheng, D.L.Mon, Fuzzy system reliability analysis byinterval of con fi dence, Fuzzy Sets Syst.56 (1)(1993) 29-35.

[6] S.M.Chen, Fuzzy system reliability analysis using fuzzy number arithmetic operations, Fuzzy Sets Syst.64 (1)(1994) 31-38.

[7] J.Knezevic, E.R.Odoom, Reliability modeling of repairable systems using petri nets and Fuzzy lambda-tau methodology, Reliab.Eng.Syst.Safety 73 (1) (2001) 1-17.

[8] K.S.Wang, H.J.Po,F.S.Hsu, C.S.Liu, Analysis of equivalent dynamic reliability with repairs under partial information, Reliab.Eng.Syst.Safety 76 (1) (2002) 29-42.

[9] O.P.Yadav, N.Singh, R.B.Chinnam, P.S.Goel, A fuzzy logic based approach to reliability improvement estimation during product development, Reliab.Eng.Syst.Safety 80 (1)(2003) 63-74.

[10] Q.Jiang, C.-H.Chen, A numerical algorithm of fuzzy reliability, Reliab.Eng.Syst.Safety 80 (3)(2003) 299-307.

[11] M.Tanrioven, Q.W u, D.Turner, C.Kocatepe, J.W ang, A new approach to real-time reliability analysis oftransmission system using fuzzy Markov model, Int.J.Elect.Power Energy Syst.26 (10) (2004) 821-832.

[12] R.Zhao, B.Liu, Standby redundancy optimization problems with fuzzy lifetimes, Comput.Indust.Eng.49 (2)(2005) 318-338.

[13] H.-Z.Huang, M.J.Zuo,Z.-Q.Sun, Bayesian reliability analysis for fuzzy lifetime data, Fuzzy Sets Syst.157 (12) (2006) 1674-1686.

[14] K.D.Rao,V.Gopika, H.Kushwaha, A.Verma, A.Srividya, Test interval optimizationofsafety systems ofnuclear power plant using fuzzy-genetic approach, Reliab.Eng.Syst.Safety 92 (7)(2007) 895-901.

[15] J.-C.Ke, H.-I.Huang, C.-H.Lin, A redundant repairable system with imperfect coverage and fuzzy parameters, Appl.Math.Modell.32 (12) (2008) 2839-2850.

[16] S.W ang, J.W atada, Modelling redundancy allocation fora fuzzy random parallel-series system, J.Comput.Appl.Math.232 (2)(2009) 539-557.

[17] Komal, S.Sharma, D.Kumar, RAM analysis of repairable industrial systems utilizing uncertain data, Appl.SoftComput.10 (4)(2010) 1208-1221.

[18] S.Taheri, R.Zarei, Bayesian system reliability assessment under the vague environment, Appl.SoftComput.11 (2)(2011) 1614-1622.

[19] N.Kumar, J.-H.Borm, A.Kumar, Reliability analysis of waste cleanup manipulator using genetic algorithms and fuzzy methodology, Comput.Oper.Res.39 (2)(2012) 310-319.

[20] M.Konstandinidou, Z.N ivolianitou, C.Kiranoudis, N.Markatos, A fuzzy modeling application ofcream methodology forhuman reliability analysis, Reliab.Eng.Syst.Safety 91 (6)(2006) 706-716.

[21] M.Bertolini, Assessment of human reliability factors: a fuzzy cognitive maps approach, Int.J.Indus.Ergonom.37 (5)(2007) 405-413.

[22] P.-C.Li, G.hua Chen, L.cao Dai,Z.Li, Fuzzy logic-based approach foridentifying the risk importance of human error, Safety Sci.48 (7) (2010) 902-913.

[23] Y.C.Hsieh, T.C.Chen, D.L.Bricker, Genetic algorithms forreliability design problems, Microelect.Reliab.38 (1998) 1599-1605