无序光子晶体提高GaN基蓝光发光二极管光提取效率的研究*

陈新莲 孔凡敏 李康 高晖 岳庆炀

1)(山东大学信息科学与工程学院，济南 250100)

2)(济南大学物理科学与技术学院，济南 250022)

(2012年2月7日收到;2012年7月29日收到修改稿)

1 引言

发光二极管(LED)作为一种半导体固体发光器件，具有环保节能、坚固耐用、可靠性高、体积小等诸多优点，在照明、通信、国防、医疗等领域有着广泛的应用前景[1,2].GaN基蓝光LED可作为白光照明的光源，很有可能替代白炽灯和荧光灯而成为新一代的绿色照明能源.由于GaN材料与空气折射率之间大的差异所引起的全内反射和Fresnel反射，有源层产生的光大部分陷落在半导体材料内部而转变为热能耗散掉，导致LED的外量子效率极差.LED的外量子效率(EQE)由内量子效率(IQE)和光提取效率(LEE)两部分相乘而得.目前对蓝光LED在波长450 nm IQE可以达到80%以上[3].较低的光提取效率成为限制其应用的主要瓶颈.已有大量文献报道了提高LEE的方法与技术，主要有倒装结构[4-6]、倒金字塔结构[7]、表面粗化[1,8]、光子晶体(PhCs)[9]等.表面粗化可以削弱全内反射限制，让更多的光经粗糙表面散射而逃逸出来，此方面的研究工作多集中在实验方面.近年来在LED顶端刻蚀PhCs的方法得到了广泛研究.虽然表面PhCs制作工艺水平越来越高，但在亚波长尺度，不可避免地会出现结构上的缺陷和无序，如空气孔圆柱的中心位置偏离格点位置、空气孔的半径及深度起伏等，这种无序变化会严重影响光子晶体的性能，使其出现一些新的特性，例如光子局域化就是由于在无序光子晶体中多重散射的光发生干涉造成的[10].近年来，由这种无序引起的光子晶体的特性在理论和实验上得到广泛研究.其主要研究工作集中在无序光子晶体中光传播的局域化特性[11,12]及其电磁模式[13]研究方面，有关光子晶体结构参数的无序变化量对LED光提取效率影响研究较少.本文研究了光子晶体的结构参数的无序变化对LED LEE的影响，以期为高性能蓝光PhCs LED的制作提供参考.

本文首先阐述了模拟构建的GaN基LED模型及其采用的计算方法，优化了有源层的位置及PhCs的空气孔半径;然后分析了位置无序变化、半径无序变化及深度无序变化对蓝光GaN基LED LEE的影响，并对结果从理论上给予解释和分析.

2 模型与计算方法

二维理想方形晶格光子晶体LED结构如图1所示.图1(a)为LED沿纵切面的结构示意图，图1(b)为理想的二维PhCs结构俯视图，自下而上依次为蓝宝石衬底、N-GaN、有源层和P-GaN，其中蓝宝石衬底厚度为1000 nm，N-GaN和P-GaN厚度为2000 nm.此外，表面PhCs的刻蚀深度为H0=350nm.计算采用中心波长为465 nm的蓝光，PhCs的晶格常数为a=200 nm保持不变，空气孔的半径为R0.

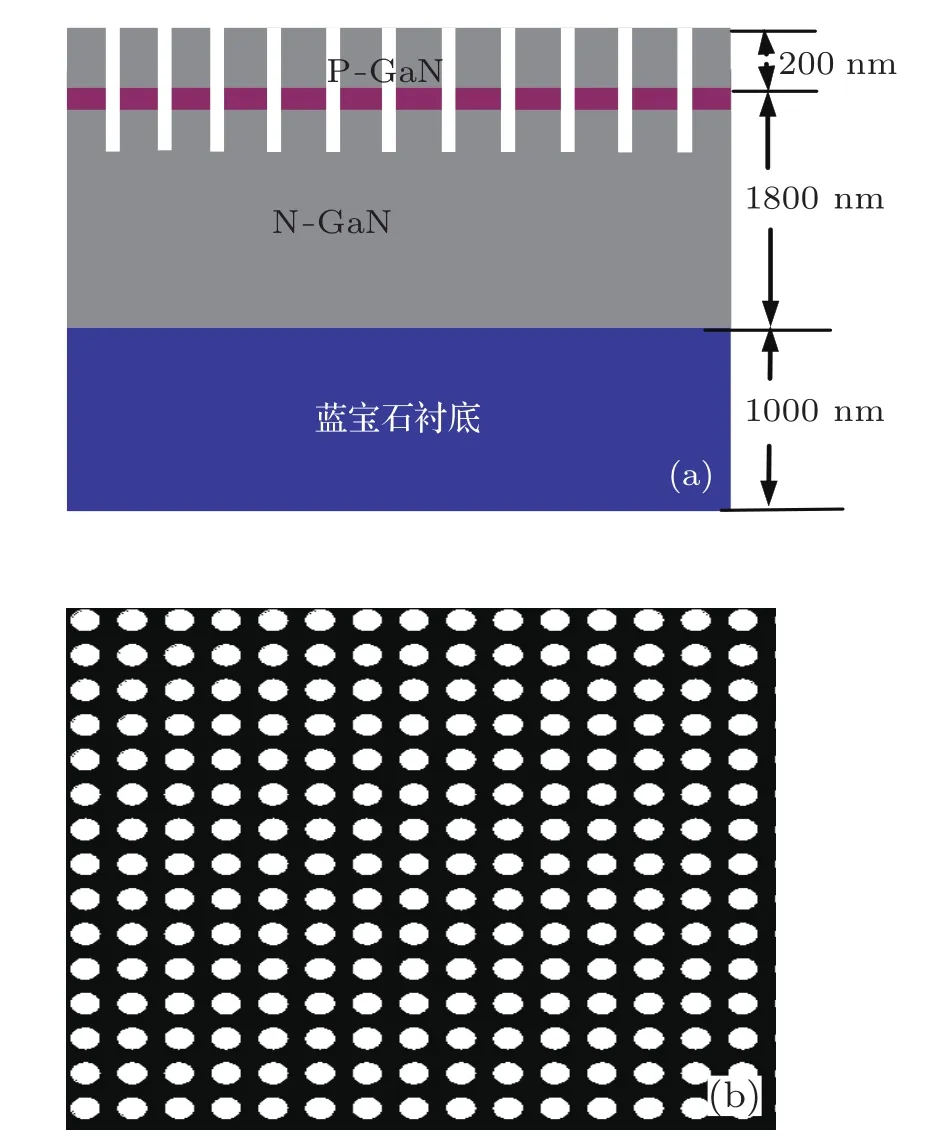
图1 二维理想方形晶格空气孔型光子晶体LED结构 (a)LED沿纵切面的结构示意图;(b)理想的二维光子晶体结构

对于二维无序PhCs结构，规定PhCs的空气孔的中心位置限制在200 nm×200 nm的方形区域内变化，用随机函数来模拟PhCs结构参数的无序变化[14,15]，无序变化的空气孔中心位置的坐标(x,y)可表示为

其中i,j=1，2，3，···，分别表示在x和y方向产生的空气孔的序号，imax，jmax分别为i，j的最大取值.Rnd为通过计算机产生的0到1之间的随机数，Dx和Dy分别表示在x和y方向无序变化量，为了简便，本文计算过程中取Dx=Dy.

无序变化的PhCs的空气孔半径和刻蚀深度分别用R和H表示，其定义如下：

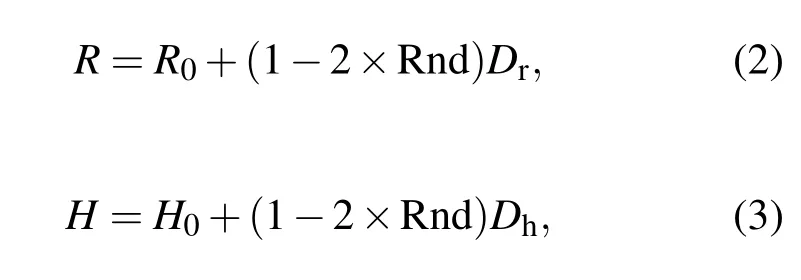
其中，Dr和Dh分别表示空气孔半径和刻蚀深度的无序变化量.

本文计算采用时域有限差分(FDTD)方法，用水平放置的电偶极子源模拟LED结构中电子-空穴复合发光.由于LED光源的非相干性和FDTD算法自身的特性，若在有源区选择多个电偶极子源或者引入周期性边界条件都将不可避免地产生非物理特性的干涉模式，导致计算结果失真，故本文只选择了单个电偶极子源模拟LED有源层.在FDTD的数值模拟中，由于目前计算机内存资源的限制，模拟实际的LED结构是不可能的.本文综合考虑仿真中数据所占内存及消耗时间的问题，仅在有限区域内对LED的能量分布进行数值计算.同时文献[16］证明，较大区域内LED的能量分布计算可以在较小区域范围内进行，故本文选取模拟区域横向空间大小为4000 nm×4000 nm，在计算区域四周添加了完美匹配层(PML)，以此避免截断边界处外来波和非电磁反射的影响.为了使计算结果尽量准确，本文计算中采用了至少3次计算结果的平均值.

LED顶端的LEE定义为

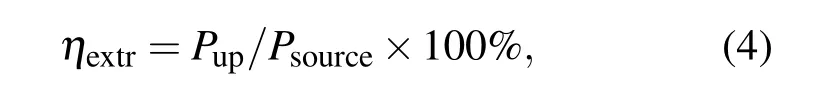
其中，Pup是LED顶端出光面法向功率积分值，即LED顶端辐射功率;Psource是包围电偶极子立方体的六个表面处向体外出射的功率的法向积分总和.另外，考虑到GaN介质的折射率虚部在蓝光频段近似为零[17]，所以计算中忽略了由GaN材料引起的功率损耗.

3 计算结果及分析

3.1 LED结构有源层位置和PhCs空气孔半径的优化

3.1.1 LED结构有源层位置的优化

对有源层的位置进行优化是为了消除PhCs刻蚀带来的上下两个界面上反射造成的影响.其实PhCs就像一个增透膜，有源层距出光面位置的改变就相当于这层增透膜厚度的改变，势必会对出光效率造成很大的影响，所以很有必要优化有源层的位置.图2考虑了当光子晶体的空气孔半径有一定的无序变化(60 nm≤R≤90 nm)时LEE随有源层距P-GaN上表面的距离dP-GaN的变化关系.通过计算可以发现，将有源层置于距P-GaN层上表面为200 nm时，顶端光提取效率最佳，最高的LEE达24.79%，与没有结构的平板LED相比LEE增加了6倍以上.实际上，200nm的长度近似为蓝光在GaN材料一个波长的长度∼λ/n(λ和n分别为空气中光的波长和材料的有效折射率)，这是经有源层发出的光到达P-GaN的上表面与从上表面反射的光发生干涉相长导致的.源的位置对LEE的影响与文献[18］给出的平板结构的情况相一致.无序PhCs的出现并未改变有源层的位置对LEE的影响.本文下面的计算均设定有源层距P-GaN层上表面的距离dP-GaN=200 nm.

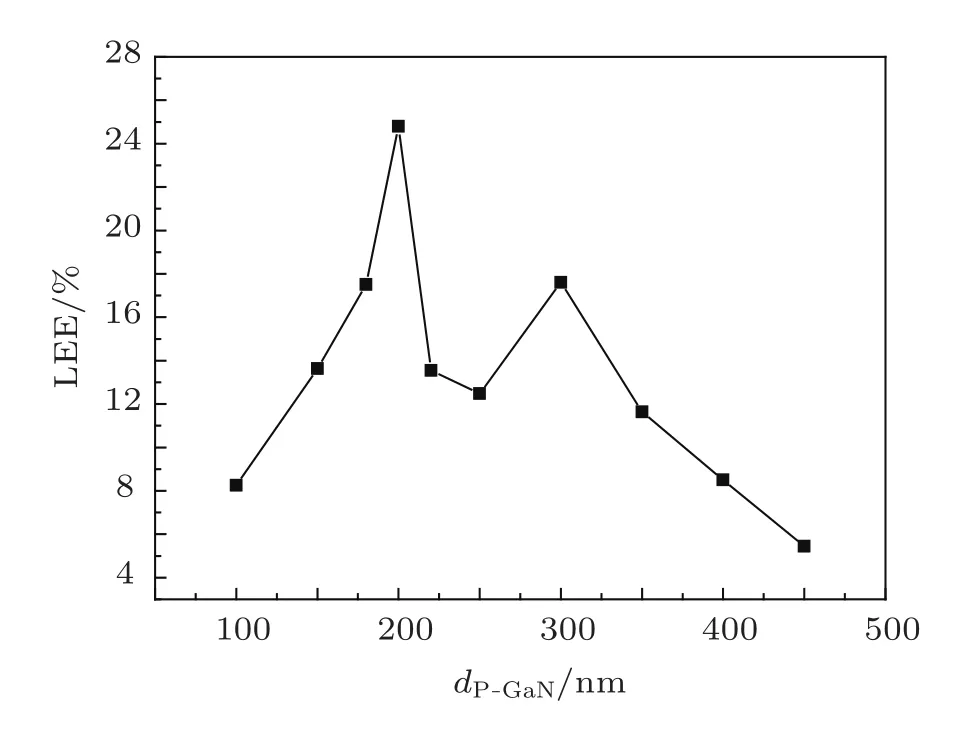
图2 光提取效率随dP-GaN的变化关系

3.1.2 PhCs空气孔半径的优化

理想方形PhCs的填充因子f=πR20/a2，R0为空气孔半径，a为晶格常数.当a一定时，f只与R0有关.

图3为LEE随空气孔半径R0的变化关系.为了后面的讨论，同时给出了填充因子f随R0的变化关系.由图3可以看出，在R0≤60 nm时，LEE随R0的增加而缓慢增加，当60 nm＜R0＜80 nm时LEE增加较快，当R0=80 nm时达到最大.R0=60 nm时对应的LEE为11.66%，此时填充因子f≈0.28;当R0=80 nm时光提取效率到达极大值，其值为28.71%，对应的填充因子f≈0.50.这表明填充因子对P hCs LED的LEE起着重要的作用，在晶格常数a一定时，空气孔过大或过小都不利于光的提取.

为了充分研究PhCs的结构参数的无序变化对LEE的影响，在保持a=200 nm不变的情况下，分别选择了非优化的半径R0=60 nm和优化半径R0=80 nm进行比较.之所以选择这两个半径进行比较，是因为由图3可以发现R0=60 nm是LEE缓慢变化与较快变化的一个转折位置;而R0=80 nm是LEE效率最高的半径宽度.

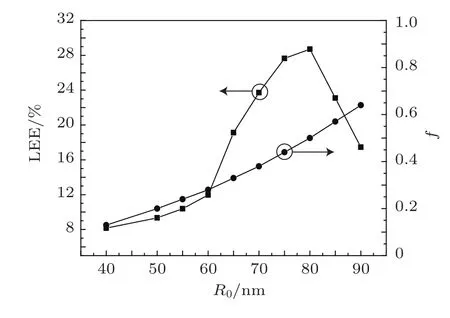
图3 光提取效率随空气孔半径R0的变化关系

3.2 空气孔半径不变,位置无序对LED光提取效率的影响

图4为由(1)式得到的当半径R0=60和80 nm、无序变化量Dx或Dy分别为20和40 nm时无序PhCs结构图.对于R0=60 nm的PhCs，为了避免在产生无序PhCs的过程中空气孔的重叠，其位置无序变化量最大为40 nm，相应地，R0=80 nm PhCs其位置的无序变量最大为20 nm.

图5是LEE随PhCs位置无序量Dx的变化关系.图5(a)为R0=60 nm时LEE随Dx的变化关系，虚线表示理想PhCs的结果，点划线表示有无序变化时计算结果的平均值，细竖线表示计算结果的浮动范围(以下相同).可以看出，R0=60 nm的无序PhCs LED其LEE略有增加，但不明显.因为当导模的波矢k//满足公式|k//+mG|＜k0的衍射条件时[19]，可以通过光的衍射使导模变成辐射模，式中k//为平面内导模的波矢，G=2π/a是晶格矢量.空气孔中心位置的无序变化，破坏了理想光子晶体的周期结构，a发生了变化，G相应地有一定的变化，致使有更多的导模被衍射成辐射模，使LEE增加.但由于计算过程中无序变化量Dx变化范围不大(≤40 nm)，以致a的变化范围并不大，所以增加的LEE能够满足衍射条件的导模有限，使得LEE有增加但变化不明显.图5(b)为R0=60和80 nm时LEE随Dx的变化关系.R0=80 nm时PhCs位置无序变化量对LEE的影响与R0=60 nm时规律相反，LEE随Dx的增加而减小，并且对位置无序变化的影响更敏感.这是因为对于R0=80 nm的无序光子晶体，位置的无序变化破坏了PhCs与导模的最佳耦合，使LEE随Dx的增加而减小;而对于R0=60nm的情况，位置的无序变化改变了晶格矢量，增加了满足衍射条件导模的数量，从而使LEE增加.

图4 位置无序时光子晶体结构 (a)R0=60 nm，Dx=40 nm;(b)R0=80 nm，Dx=20 nm

图5 光提取效率随Dx的变化关系 (a)R0=60 nm时光提取效率随Dx的变化关系;(b)R0=60和80 nm时光提取效率随Dx的变化关系

3.3 空气孔的中心位置不变,半径无序变化对LED光提取效率的影响

图6是由(2)式得到的当半径R0分别为60和80 nm，无序变量Dr均为20nm时无序PhCs的结构图，图7为对该结构计算得到的LEE随Dr的变化关系.图7(a)给出了当R0=60 nm时LEE随Dr的变化关系，虚线表示理想PhCs LED的LEE.从图中可以看出LEE随着Dr的增加而增加，当Dr从0增加到20 nm时LEE从11.66%增到17.93%，提高了53.8%.图7(b)比较了R0分别为60和80 nm时半径无序变化对LEE的影响.当R0=80 nm时LEE随着Dr的增加而减小，当Dr从0变到20 nm时，LEE从28.71%降到20.05%，降低了30%.由此可见，PhCs空气孔半径的无序变化使优化的80 nm空气孔PhCs LED的LEE下降，而可使非优化的60 nm空气孔PhCs LED的LEE增加.这是因为从图3可以发现，R0=60 nm时，当空气孔半径存在无序变化时，即使在60 nm两侧有相同的变化量，但由于半径大于60 nm后光提取效率增加速度要明显快于半径小于60 nm的情形，所以半径的无序使得60 nm孔径LED的光提取效率增加.而对于优化的R0=80 nm时，半径的任何无序都会使光提取效率降低.这进一步证明，晶格常数a确定时，必对应特定优化的空气孔半径，使PhCs LED可以获得最大的LEE.

图7 光提取效率随Dr的变化关系 (a)R0=60 nm时光提取效率随Dr的变化关系;(b)R0=60和80 nm时光提取效率随Dr的变化关系

3.4 空气孔的中心位置、半径不变,刻蚀深度的无序变化对光提取效率的影响

图8计算了由(3)式得到的当PhCs的刻蚀深度存在无序变化时LEE随Dh的变化关系.虚线为相应的理想PhCs LED的LEE.由图8可以看出，当PhCs的刻蚀深度有一定的无序变化时，光提取效率相对于理想光子晶体而言略有降低，但其变化均在1%—2%之间.因此在LED PhCs的制作中，可以忽略刻蚀深度的不准确对LED的LEE的影响.

综合前面的结果及分析不难发现，PhCs的空气孔位置、半径及刻蚀深度等结构参数的无序变化对LED LEE有不同程度的影响，在PhCs加工工艺允许的误差下，结合FDTD方法通过对结构优化，可获得最佳LEE的LED.

图8 光提取效率随Dh的变化关系

4 结论

本文利用FDTD方法研究了二维光子晶体空气孔位置、半径和刻蚀深度的无序变化对GaN基蓝光LED LEE的影响.研究结果表明，空气孔位置变化一般呈现弱无序状态，其对LEE的影响不显著;空气孔半径的无序变化可以显著地影响LED的LEE，最大变化幅度可达53.8%;空气孔在深度刻蚀情况下，其刻蚀深度在20%的范围无序变化时，对LEE的影响可以忽略;通过比较R0=60和80 nm的PhCs的位置、半径和刻蚀深度的无序变化对LEE影响，得到位置和半径的无序变化会使得R0=60 nm的PhCs的LEE增加，而使R0=80 nm的PhCs的LEE减小.这说明不同结构参数的PhCs LED受结构参数无序变化的影响不同，但每个PhCs LED会存在一组优化参数，使其LEE达到最大，其他PhCs结构参数的无序变化都会使LEE减小.

[1］Schubert E F 2006Light-Emitting Diodes(New York：Cambridge University Press)p21

[2］ Fang Z l，Qin J M 1992Semiconductor Light-Emitting Material and Device(Shanghai：Fudan Univerty Press)[方志烈，秦金妹 1992 半导体发光材料和器件(上海：复旦大学出版社)］

[3］DepartmentofEnergy 2008SolidStateLightingResearch andDevelopmentMulti-YearProgramPlanFY’09-FY’14＜http：//www.1eere.energy.gov/buildings/ssl/projects.html＞2012.2.7

[4］ Wierer J J，Steigerwald D A，Krames M R，O’Shea J J，Ludowise M J，Christenson G，Shen Y C，Lowery C，Martin P S，Subramanya S，Gotz W，Gardne N F，Kern R S，Stockman S A 2001Appl.Phys.Lett.78 3379

[5］Shchekin O B，Epler J E，Trottier T A，Margalith T，Steigerwald D A，Holcomb M O，Martin P S，Krames M R 2006Appl.Phys.Lett.89 071109

[6］Chao C H，Chuang S L，Wu T L 2006Appl.Phys.Lett.89 091116

[7］Krames M R，Ochiai-Holcomb M，H¨o fler G E，Carter-Coman C，Chen E I，Tan I H，Tan T S，Kocot C P，Hueschen M，Posselt J，Loh B，Sasser G，Collins D 1999Appl.Phys.Lett.75 2365

[8］Fujii T，Gao Y，Sharma R，Hu E L，Denbaars S P，Nakamura S 2004Appl.Phys.Lett.84 855

[9］Matioli E，Weisbuch C 2010J.Phys.D：Appl.Phys.43 354005

[10］Xu X S，Chen H D，Zhang D Z 2006Acta Phys.Sin.55 6433(in Chinese)[许兴胜，陈宏达，张道中2006物理学报55 6433］

[11］Raedt H D，Lagendijk A，Vries P D 1989Phys.Rev.Lett.62 47

[12］Wang B W，Jin Y，He S L 2009J.Appl.Phys.106 014508

[13］Savona V 2011Phys.Rev.B 85 085301

[14］Long D H，Hwang I K，Ryu S W 2009IEEE J.Sel.Top.Quan.Elec.15 1257

[15］Long D H，Kag H I，Wan S 2008Jpn.J.Appl.Phys.47 4527

[16］Wiesmann C 2009Ph.D.Dissertation(Regensburg：Regensburg Universit¨at)

[17］K¨ohler U，As D J，Sch¨ottker B，Frey T，Lischka K，Scheiner J，Shokhovets S，Goldhahn R 1999J.Appl.Phys.85 404

[18］Ryu H Y 2009J.Kore Phys.Soci.55 2644

[19］Matiolio E，Fleury B，Rangel E，Melo T，Hu E，Speck J，Weisbuch C 2010Appl.Phys.Exp.3 032103