模型二元有序合金固液界面结构的分子动力学研究*

郑小青 杨洋 孙得彦

(华东师范大学物理系，上海 200241)

(2012年4月6日收到;2012年7月26日收到修改稿)

1 引言

固液界面结构的研究对认识凝聚态物理中的许多现象有重要的科学意义，例如固化、外延生长、浸润、晶体生长等[1-3].当液体附着在晶体表面时，晶体的周期性结构通常会驱使其附近的液体产生有序结构.理论研究已预测了这种有序行为的存在[4-7]，其中一些预测已得到了实验的证实[8-13].晶体引起的界面附近液体的有序结构可分为两种类型：即垂直于界面方向的密度有序和平行于界面方向的原子二维有序.在基于X射线散射以及电子显微技术的实验中已经观察到了这种垂直于界面方向的密度有序[14-17].另外，界面层液体的二维有序也在一些实验和模拟研究中得到了证实[17].例如，在Pb和Sn的单原子层附着在Ge(111)晶体表面的简单体系中，就能观察到液体的二维有序结构[8,9,18].利用透射电子显微技术，人们在Si表面吸附的液体Al-Si合金体系中也观察到液体的二维有序化现象[19].最近人们利用高分辨透射电子显微镜在氧化铝和液体铝组成的界面体系中[20]同时观察到液体在垂直界面方向的密度有序和平行于界面方向的二维结构有序.该实验还发现液体的二维有序只在界面附近的三层液体中存在，明显比垂直于界面方向的密度有序衰减得更快.

迄今为止，对界面处液体有序性的实验研究主要集中在异质固液界面体系，即固相和液相有着完全不同的化学组成.对于固液相成分相同的界面，实验上很难直接测量其结构特征.目前，对这类界面结构的研究主要是通过计算机模拟来实现[17,21].固液界面的模拟研究已在许多体系中开展，比如硬球体系[7]，LJ(Lennard-Jones)体系[22,23]和许多简单金属体系[24-26]，也包括大量对异质界面体系的模拟研究[27-30].尽管合金体系通常会更有趣，但到目前为止，对多元合金体系界面有序性的研究却很少[31-38].

本文采用分子动力学方法研究了LJ模型二元有序合金固液界面的结构与原子扩散.选择此体系作为研究对象，主要基于三方面的考虑.第一，对有序合金固液界面而言，界面附近通常有多个序参量同时发生变化，比如结构序、化学序(不同化学元素的规则排布)、磁有序等.这些晶体中的序参量是如何协同影响液体结构的，目前还少有报道.在当前的体系中，晶体同时具有结构和化学序的变化，有可能引起液体里结构和化学序的反常存在，这种现象在前人的研究中几乎没讨论过.第二，该模型二元有序合金体系的固液界面是光滑界面(faceted interface).已有的对界面液体有序性的实验或者模拟研究中，涉及的界面多是粗糙界面(rough interface)，而对合金体系光滑界面的研究却很少.然而，对于合金光滑界面来说，界面附近液体层的二维有序结构可能更为复杂.第三，该二元有序合金代表了一大类二元有序半导体的结构.研究当前体系对认识该类半导体沿(111)方向的固化与生长有积极的意义.本文中，为获得体系界面附近液体的结构特征，计算了垂直于界面方向的密度和结构序分布.通过分析二维径向分布函数、二维密度和结构因子等，研究了界面层的二维结构信息.最后通过计算扩散系数研究了界面附近原子的扩散行为.我们的研究结果表明固体的结构序和化学有序对界面结构有强烈的调制作用.

2 研究方法

2.1 势函数的选取和分子动力学模拟细节

模型二元合金由A，B两种元素组成，它们之间的相互作用势用所谓截断LJ势来描述，其中的LJ势参数取自文献[39］.根据该文献，A原子与B原子之间的相互作用满足关系：σAA=σBB，εAA=εBB且εAB=eεAA，σAB=sσAA，其中参数e=1 和s=1.2分别描述原子A与B之间的相对相互作用强度和相对距离.为了方便计算，使用一个真实的单位(氩的LJ参数)来代替约化单位.取粒子之间的相互作用势参数εAA/kB=114.1 K和σAA=0.3405 nm.根据文献[39］，此时体系的固液转变温度为72 K.有趣的是，该体系属于congruent-melting，即在熔点液体和固体有相同的化学成分.对应于上面的势参数，二元合金具有所谓的fcc(111)-layered结构，此结构指的是A，B两种原子在fcc(111)方向上交替排列.该结构可以看作扭曲的闪锌矿结构，其中(111)方向的层间距有所变化.该结构合金在二元半导体中广泛存在，在核辐射检测技术中所使用的melt-grown化合物半导体，例如CdTe，即属于该类有序合金[38].在这类合金中，AB原子比较相近，这正是本文中的模型所具有的独特性.在一定程度上，尽管简单的LJ势也许难以和复杂的多体势相比，但它的形式简单、物理明确的特点仍使它被广泛采用.事实上，在对固液界面的研究中，简单LJ势往往可以获得和实验可比的结果[22,23].

所有的分子动力学模拟都采用LAMMPS(大尺度原子/分子的大规模并行计算)程序，时间步长取为1 fs[40].模拟体系的z轴方向垂直于固液界面，另两个平行于固液界面的方向为x和y坐标轴，三个坐标轴方向上均采用周期性边界条件.模拟体系的具体尺寸为76.35˚A×79.34˚A×338.28˚A，共包含36000个原子.

为建立平衡固液共存体系，首先按照上面的尺寸产生完全有序的fcc(111)-layered结构的晶体.完整的晶体建立以后，沿着模拟体系最长方向(z方向)将大约1/2的晶体在一个非常高的温度下熔化，而剩余的原子被固定在晶格位上.接下来，允许所有原子运动，并将整个体系的温度降到72 K进行热力学平衡，此过程用的是NPzAT系综(即平行于界面方向的周期长度保持一个固定值，垂直于界面方向的周期长度是动力学变化的，为了使体系在此方向上保持零压，该系综是固液界面研究中常用的[27,41,42]).最后将体系在NVE系综下进行长时间的平衡.演化平衡后体系稳定在72 K，此值即为固液共存的温度，也即熔点.该值与文献[39］中给出的72 K一致.在体系达到完全平衡后，在72 K体系持续50 ns的时间演化.所有的计算都是在这50 ns的平衡过程中进行的.最后建立的固液共存体系的原子坐标快照如图1所示，图中体系已处在固液两相平衡态.

图1 模型二元有序合金体系固液共存原子坐标快照 图中红色的实心点代表A原子，蓝色的空心点代表B原子，可以看出清晰的固液界面;箭头所指的层为界面过渡层

2.2 数密度与序参量的计算

为了描述界面的结构特征，我们计算了粒子数密度和结构序沿z方向的分布.这些分布可以刻画对应的物理量在穿过固液界面时的变化规律.我们具体计算了两种类型的分布：精细分布( fine-scale pro file)和经滤波法光滑的粗粒分布(coarse-grained pro files).在精细分布的计算中，首先将体系沿着z方向划分为很多等厚度的薄层，然后计算每个薄层内的物理量的平均值，最后这些平均值随z的变化就构成了对应物理量的精细分布.在计算中，薄层的厚度Δz取为界面法向方向层间距的1/40.为了得到各物理量的粗粒分布，采用了有限脉冲响应滤波法 ( finite-impulse-response filter，FIR)，有关该方法的技术细节见文献[7,42].FIR方法的关键是选择合适的N和ε的值，它们是控制平均加权范围的参数.用文献[42］的方法，对当前体系我们发现N=60和ε=145是最佳值.

数密度分布是分析固液界面处法向有序的重要物理量[32-34,42].我们分别计算了每个薄层中A原子数密度，B原子数密度与总的数密度.数密度的计算是通过50 ns的分子动力学模拟得到的.

为了分析结构变化的有序程度，还计算了结构序参量的分布.本文采用Hoyt等[25]在2001年提出的结构序参量来区分固液相原子.以前的研究表明，该序参量对bcc和fcc结构的晶体非常有效[43].根据文献[25］，第i个原子的序参量定义为，其中，N是原子的最近邻数目，rij是i原子与原子j之间的距离，而rideal代表该两原子在完美晶格中的最近邻位置.对当前关心的结构而言，取N=12.为求结构序参量的精细分布，对每个薄层里所有原子的序参量进行平均，平均历经50 ns的分子动力学模拟.

2.3 界面二维结构的描述

除了计算各物理量沿着z方向的分布外，还研究了界面处液体在平行于界面方向的二维结构.具体地，计算了二维径向分布函数、二维密度和二维结构因子[44].这些量的计算主要集中在界面附近的几层原子，具体计算方法与传统方法类似.惟一不同的是，此时原子位置仅由x和y方向的坐标决定.也就是说，此时这些界面层中的原子被投影到xy平面上.例如，二维径向分布函数的计算与三维情况相同，除了原子i与j之间的距离被定义为最后对这一层内的所有原子求平均值，平均用的分子动力学模拟时间为50 ns.为了计算二维密度ρxy(r)，将每一层划分为许多二维的格子(大约是200×200个)，计算每个格子里原子的平均密度.二维密度的计算通过500 ps的平均获得.得到二维密度后，二维结构因子Fxy(k)通过下式很容易计算：

其中，ρxy(k)是每个构型的二维密度的傅里叶变换.

2.4 扩散系数的计算

为了计算扩散系数在界面附近的变化，首先将体系沿着z方向划分为较大的区间，区间的大小大致相当于晶体中的面间距，这些区间由精细密度分布的最小值确定.对每个区间，计算该区间内每个粒子的均方位移粒子最初处在此区间中的时刻记为t=t0，每个区间的扩散系数由原子的均方位移随时间变化的斜率得到，即：

〈〉z表示对不同时间起点(t0)的平均，这里这个平均进行了10次.为研究扩散的各向异性，本文还计算了x，y和z三个方向的扩散系数.具体计算某一方向的扩散系数时，均方位移(MSD)仅包括该方向上原子位移的贡献.上面有关计算界面处原子扩散系数的方法在文献[27，32—34］中常用.

3 计算结果与讨论

3.1 密度和结构序的分布

图2是精细数密度沿界面法向方向的分布.从图中可以看出，在远离固液界面处，三种数密度在固体区域呈规则的周期振荡，并且A原子层和B原子层交替出现，两种元素的密度呈现出的这种交替排列的特征是晶体结构的反映.而在远离界面的液体区域，密度呈现平滑的分布，这正是典型合金液体的结构特征.

密度分布在界面附近的液体区域仍有明显的波动，并且这些波动在进入液体区域大约30˚A后才基本消失.这些密度波动的存在说明界面处的液体具有一定的有序性.虽然密度波动在通常的固液界面处广泛存在，但目前的密度波动呈现出一些异质界面和单质固液界面所没有的新特征.这些新特征体现在：第一，尽管总密度(图2中的实线)有类似单质中的周期密度波动，但液体中的密度峰明显不对称，例如，图2中d层峰的左边明显有“肩膀”存在，这说明界面处液体不是简单的无序合金液体;第二，液体没有呈现出简单的A原子和B原子密度交替振荡，从c层开始，总密度的波动与A，B原子密度的波动也不完全一致，例如在界面附近连续的两层即d层和e层中，A原子的密度占主导，而c层以B原子为主;第三，微观看来，界面处的液体层(c—g)由两个沿z方向相互分开的亚层组成.例如，d层的总密度就是由两个明显分开的A原子密度峰和B原子密度峰组成.

图2 模型二元有序合金体系固液界面密度的精细分布 实线代表总密度，点线代表A原子的密度，虚线代表B原子的密度;界面附近的几层用 a，b，c，d，e，f和 g 标记，c 层为过渡层，对应图1中箭头所指的层

就异质或单质固液界面而言，液体中的密度波动主要是由固体中的周期结构引起的.而目前的系统中，固体不仅具有结构上的周期性，同时具有所谓的化学序，这正是当前界面处液体密度变化的主要原因.固体的周期结构驱使界面处液体密度的周期波动，这可由图2中总密度的变化看出.而固体中的化学有序同样有驱使界面处液体保留化学序的趋势，这可以从界面附近液体A原子和B原子密度并不是完全无序看出.当然液体本身具有结构和化学无序的趋势，这种无序的动力来自无序导致的熵增加，从而降低液体的自由能.这种固体驱使的有序和熵驱使的无序的竞争导致界面处液体的复杂的密度波动.可以看出，结构序显然比化学序对密度的影响要强一些.因为总密度的波动和固体中的密度波动大体一致，而A原子B原子的密度波动并不完全符合固体中的密度波动.前者主要由结构序引起，而后者主要是化学序导致.这些竞争还导致一些亚层的出现，例如层c，d和e中出现的亚层对应图2中这些层包含的两种原子形成的两个峰.我们还将在后面有关的结构分析中进一步阐述.

界面的有效宽度是刻画界面特征的一个重要物理量.界面的空间分布范围通常由粗粒密度分布的10—90宽度来衡量[33,34,42].10—90宽度定义为：块体在固相的数密度ρs相对于液相的数密度ρl从10%变化到90%时，对应的z方向的距离.用双曲正切函数拟合界面附近的粗粒密度分布，就可得到界面的10—90宽度.根据文献[42］，可以计算两种界面宽度：即固有宽度和平均宽度.固有宽度是每个时刻密度的粗粒分布对应的10—90宽度的平均值.平均宽度是将所有时刻的密度求平均，获得精细密度分布后再求密度的粗粒分布对应的10—90宽度.

对同一个体系来说，密度固有宽度和平均宽度的差异是在原子尺度上衡量界面特征的重要指标，例如光滑界面还是粗糙界面.正如Buta等[42]讨论的，这两种宽度的差异与平衡态熔化和固化涨落导致的界面净移动有密切关系.如果净移动可以忽略，也就是这两种宽度差别很小时，表明此时界面是光滑界面.相反，对粗糙界面来说，这两种宽度存在明显的差异，也就是说界面存在不可忽略的净移动.可通过对比这两种宽度来确定界面是光滑界面还是粗糙界面.通过计算，我们获得该体系固液界面的固有宽度和平均宽度分别为12.84˚A和12.91˚A，说明这时界面在原子尺度上是光滑的.事实上，关于光滑界面可以清楚地从图1中看出.

图3 模型二元有序合金的密度和结构序的粗粒分布 实线φ∗(z)和虚线ρ∗(z)分别代表经过转化、归一的结构序和数密度分布

结构序参量也常用来研究固液界面的结构特征.图3给出结构序参量和密度的粗粒分布.图中的数据通过转化、归一使得固体对应的值为0而液体对应的值为1.通过对比可以看出，结构序和密度在界面附近彼此相交，这表明在界面附近，先是数密度的变化较快，到了一定的位置后，结构序反而变化得更快.如果我们定义结构序参量的平均值为界面中心的位置，可以看出，在靠近界面中心的固体端，结构更加有序但却有较低的固体密度.而在靠近界面中心的液体端，虽然结构已经非常无序但却仍有较高的液体密度.

图4 模型二元有序合金体系的二维径向分布函数，层的符号与图2密度中标记的一致

3.2 界面层的二维结构分布

为了分析界面处的二维结构特征，我们首先计算了图2中标示的b到g层的二维径向分布函数.图4是这些界面层对应的二维径向分布函数gxy(r)的计算结果.从图中可以看出，b层的gxy(r)具有典型长程有序的特点，表明这一层具有较完整的晶体结构.除了峰的高度不同外，c层和b层的二维径向分布函数非常类似，表明c层仍然以长程有序性为主，只是有序性的强度明显降低了.c层中，gxy(r)的形状与一个二维有序团簇在液体环境中很相似.然而，如果c层内二维有序团簇是随机分布的，还是不能解释gxy(r)中呈现出的长程有序.原因可能是在c层中出现的有序团簇被b层原子提供的二维周期势所约束，从而导致这些有序团簇不仅倾向于具有和晶体同样的平移对称性，同时被有效“锁定”在“正确”的晶格位上.这种现象在Si(111)光滑界面的二维径向分布函数中也被发现[42].由于化学序和熵的竞争，虽然d，e和g层表现出明显的液体特征，即长程无序.但它们仍然存在着复杂的微结构，例如它们的第一近邻峰都有明显的“肩膀”.这种复杂结构主要是由这些层具有两种原子形成的两个亚层引起的，这也可以从图2中看出.

为了深入分析界面层的二维结构，我们进一步计算了时间平均的二维密度和二维结构因子，具体结果如图5所示.从图5中四层原子的二维坐标快照和对应的二维密度分布中可以看出，a层和b层中的原子基本有序，d层基本显示出无序液体的特征，而c层的结构明显介于b和d层之间，有一定有序性的存在.

图5 模型二元有序合金体系界面层的二维结构分布 左栏：a，b，c，d这四层中原子位置的二维快照，红色的实心点代表A原子，蓝色的空心点代表B原子;中间栏：对应层的二维密度分布，图中线性灰色区域的点代表的密度范围是0到0.1˚A-3;右栏：对应四层的二维结构因子.k矢量在x和y方向上的范围分别为-100×2π/Lx到100×2π/Lx和-100×2π/Ly到100×2π/Ly

二维结构因子是分析层内原子结构的重要物理量.如图5所示，从a层到d层，晶体的对称性的强度逐渐减小.可以看出，a层中所有k值都体现出明显的晶体对称性.对于b层，晶体的对称性开始减小，但其长程有序仍然与a层的结构因子相匹配.而在c层中，较小的k值仍显示出明显的晶体对称性，而较大的k值对应着液体的各向同性.而d层的结构因子显示出基本的液体特征.从图5中还可以看出，从固体转变成液体就发生在界面附近的c层中.也就是说，平行于界面方向液体的结构序要比垂直于界面方向的密度有序减小得更快.

为了更直观地理解过渡层(c层)的复杂结构，我们研究了该层原子结构的动态变化.图6给出了该界面层的二维原子位置在几个不同时刻的快照.图中从上到下对应c层的结构序逐渐增强.从图中可以看出原子形成的二维晶体团簇，这些有序团簇被周围的液体状的原子所包围.从c(1)到c(3)这些团簇逐渐变大.团簇中的原子数目从几个到几十个不等的变化.通过对比c层在不同时刻的团簇分布图，可以看出，结构有序是随时间变化的，即存在团簇形成和破坏的动力学过程.这一现象与前面有关该层的结构因子和径向分布函数相一致.

图6 模型二元有序合金体系c层在三个不同时刻的二维原子坐标快照c(1)，c(2)和c(3)对应的时刻的结构序逐渐增强，图中红色的点(黑色)代表固体原子，绿色的点(灰色)代表液体原子，固液原子由结构序参量区分

3.3 扩散系数的分布

图7是体系界面处原子的扩散系数随界面法向距离的变化，其中图7(a)为总的扩散系数，图7(b)为原子在三个方向上的扩散系数.图中标记的最开始的7层对应图2中对应的a层到g层.从图7(a)可以看出，从固体到液体，扩散系数单调增大，并在远离界面的液体区达到饱和.最开始的两层(a和b层)的扩散系数几乎为零，表明这些层是完全有序的晶体结构，这与前面分析的结构因子的结果相符合.由于空穴和位错俘获在界面附近的区域中，扩散过程由液体里持续的原子运动变为界面处由空穴调制的扩散，所以原子在界面附近的扩散逐渐减慢.这种界面处扩散减慢的过程在前人研究固液界面的工作中有过类似的报道[7,45].

x，y和z三个方向的扩散系数(Dx，Dy和Dz)在远离界面处保持一致，这与液体的对称性相一致.在界面附近的过渡层(大约6层)中，这三个扩散分量存在明显的各向异性：Dz＜Dx，Dz＜Dy，且Dx≈Dy.界面处扩散系数的各向异性持续了大约6层.较小的Dz值可能是由界面处液体的有序结构引起，也说明这几层中平行于界面方向的二维扩散占主导.该结果与前人的有关计算类似[46].

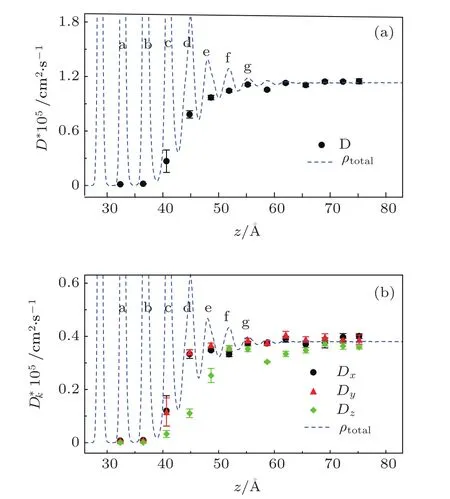
图7 模型二元有序合金体系的扩散系数 (a)总扩散系数D的分布;(b)扩散系数D的三个分量Dx(圆)，Dy(三角形)和Dz(菱形)的分布;误差代表从100个样本计算的平均值的二阶标准偏差

4 结论

采用分子动力学方法，系统研究了模型二元有序合金体系平衡固液界面的结构和原子扩散行为.为了研究界面法向方向的结构变化，计算了数密度和结构序参量沿着界面垂直方向的分布.通过分析二维径向分布函数、二维密度和二维结构因子研究了平行于界面方向上的二维原子层的结构.通过计算界面处原子的扩散系数，探索了界面附近原子的扩散行为.研究结果表明，当前的固液界面是光滑界面，即液体和固体存在一个明显的分界面.界面液体层中同时存在着垂直于界面方向的密度波动和化学有序，平行于界面方向存在一定的二维结构有序.这些有序现象和单质或异质固液界面中的有序明显不同.法向方向密度呈现A原子层和B原子层的复杂波动，这种波动形式一直延伸到液体中.对界面层的二维结构分析表明，从液体到固体的转变就发生在界面附近靠近液体的熔融层中，液体在固液转变层中形成了随时间变化的二维有序团簇.在界面附近，三个方向的扩散系数分量也显示出明显的各向异性.

[1］Liu X Y，Boek E S，Briels W J，Bennema P 1995Nature374 342

[2］Oxtoby D W 1990Nature347 725

[3］Vlieg E 2002Surf.Sci.500 458

[4］Spaepen F 1975Acta Metal.23 729

[5］Ladd A J C，Woodcock L V 1978J.Phys.C 11 3565

[6］Mori A，Manabe R，Nishioka K 1995Phys.Rev.E 51 R3831

[7］Davidchack R L，Laird B B 1998J.Chem.Phys.108 9452

[8］ de Vries S A，Goedtkindt P，Steadman P，Vlieg E 1999Phys.Rev.B 59 13301

[9］Reedijk M F，Arsic J，de Theije F K，McBride M T，Peters K F，Vlieg E 2001Phys.Rev.B 64 033403

[10］Reedijk M F，Arsic J，Hollander F F A，de Vries S A，Vlieg E 2003Phys.Rev.Lett.90 066103

[11］Arsic J，Kaminski D，Poodt P，Vlieg E 2004Phys.Rev.B 69 245406

[12］Oh S H，Kauffmann Y，Scheu C，Kaplan W D，Ruhle M 2005Science310 661

[13］Saka H，Sasaki K，Tsukimoto S，Arai S 2005J.Mater.Res.20 1629

[14］Toney M F，Howard J N，Richer J，Borges G L，Gordon J G，Melroy O R，Wiseler D G，Yee D，Sorensen L B 1994Nature368 444

[15］Huisman W J，Peters J F，Zwanenburg M J，de Vries S A，Derry T E，Abernathy D，van der Veen J F 1997Nature390 379

[16］Cheng L，Fenter P，Nagy K L，Schlegel M L，Sturchio N C 2001Phys.Rev.Lett.87 156103

[17］Kaplan W D，Kauffmann Y 2006Annu.Rev.Mater.Res.36 1

[18］Grey F，Feidenhans’l R，Pedersen J S，Nielsen M，Johnson R L 1990Phys.Rev.B 41 9519

[19］Donnelly S E，Birtcher R C，Allen C W，Morrison I，Furuya K，Song M，Mitsuishi K，Dahmen U 2002Science296 507

[20］Kauffmann Y，Oh S H，Koch C T，Hashibon A，Scheu C，Ruhle M，Kaplan W D 2011Acta Mater.59 4378

[21］Laird B B，Haymet A D J 1992Chem.Rev.92 1819

[22］Broughton J Q，Bonissent A，Abraham F F 1981J.Chem.Phys.74 4029

[23］Huitema H E A，Vlot M J，van der Eerden J P 1999J.Chem.Phys.111 4714

[24］Jesson B J，Madden P A 2000J.Chem.Phys.113 5935

[25］Hoyt J J，Asta M，Karma A 2001Phys.Rev.Lett.86 5530

[26］Becker C A，Hoyt J J，Buta D，Asta M 2007Phys.Rev.E 75 061610

[27］Palafox-Hernandez J P，Laird B B，Asta M 2011Acta Mater.59 3137

[28］Gersermans P，Gorse D，Pontikis V 2000J.Chem.Phys.113 6382

[29］Hashibon A，Adler J，Finnis M W，Kaplan W D 2002Comp.Mater.Sci.24 443

[30］Zhang X，Rice S A 2005J.Chem.Phys.123 104703

[31］Davidchack R L，Laird B B 1999Mol.Phys.97 833

[32］Davidchack R L，Laird B B 1996Phys.Rev.E 54 R5905

[33］Sibug-Aga R，Laird B B 2002J.Chem.Phys.116 3410

[34］Sibug-Aga R，Laird B B 2002Phys.Rev.B 66 144106

[35］Becker C A，Asta M，Hoyt J J，Foiles S M 2006J.Chem.Phys.124 164708

[36］Becker C A，Olmsted D L，Asta M，Hoyt J J，Foiles S M 2009Phys.Rev.B 79 054109

[37］Ramalingam H，Asta M，van de Walle A，Hoyt J J 2002Interface Sci.10 149

[38］Henager C，Morris J R 2009Phys.Rev.B 80 245309

[39］Vlot M J，van Miltenburg J C，Oonk H A J 1997J.Chem.Phys.107 10102

[40］Plimpton S J 1995J.Comput.Phys.117 1

[41］Gao Y F，Yang Y，Sun D Y，Asta M，Hoyt J J 2010J.Cryst.Growth312 3238

[42］Buta D，Asta M，Hoyt J J 2008Phys.Rev.E 78 031605

[43］Sun D Y，Asta M，Hoyt J J 2004Phys.Rev.B 69 174103

[44］Ashcroft N W，Mermin D N 1976Solid State Physics(Toronto：Thomson Learning)

[45］Broughton J Q，Gilmer G H 1986J.Chem.Phys.84 5759

[46］Yang Y，Olmsted D L，Asta M，Laird B B 2012Acta Mater.60 4960