极限存在性证明的几种主要方法*

陆永良 ， 嵇建峰

(1.平湖市城关中学, 浙江　平湖　314200；2.湖州职业技术学院, 浙江　湖州　313000)

极限是数学分析的基本概念之一,用以描述变量在一定的变化过程中的终极状态。数学分析中的几乎所有其他概念，诸如：连续、导数、微分、定积分、级数收敛性、多元函数偏导数、重积分、曲线积分、曲面积分等，都直接通过极限理论得以严密化。极限是沟通常量与变量、有限与无限的桥梁。理解极限的精确定义,掌握极限存在性证明的方法都是十分必要的，它是涉及分析的理论和计算是否可靠的基本问题。17世纪牛顿和莱布尼兹虽然完成了微积分的创立工作，但由于他们对极限概念还十分模糊，所以在微积分的基本理论上存在着明显的不严密性的缺陷，在逻辑上也有漏洞，以至于引发了第二次数学危机；直到19世纪，法国的柯西和德国的维尔斯特拉斯等人的工作，给出了极限、收敛概念的精确定义，确立了以极限论为基础的数学分析体系之后，才使微积分克服了逻辑上的困难，并使之建立在严格的理论基础之上。从此，各种极限问题才有了切实可行的判别准则。

众所周知，极限在整个微积分学乃至整个数学学科的研究中都占有举足轻重的作用，几乎都直接或间接与极限有关。证明极限的存在的方法很多，本文将把分散于数学分析各章节中的理论和方法较系统地进行归纳，并针对证明极限的存在性这个中心问题的常用解题方法进行探讨。

1　极限存在性证明的几种主要方法

极限存在性的证明是对数列极限和函数极限的存在性运用数学分析的定义和定理证明其收敛。依据不同的研究方法及所应用的数学工具，已有的极限存在性证明方法可大致分为九种，我们分别概述如下。

1.1　利用极限的基本定义证明

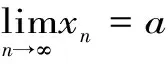
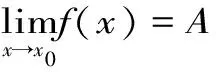
类似地，不难给定一元函数的左极限和右极限、一元函数当自变量趋于无穷大时的极限、多元函数的极限的定义。

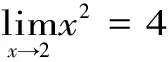
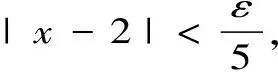
即

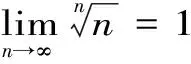
证明：根据二项式定理，得到

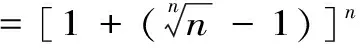
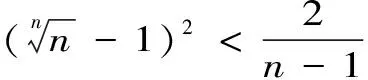
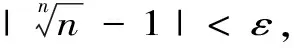
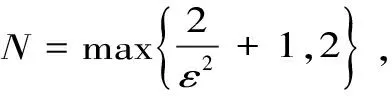
1.2　利用单调有界数列收敛定理

定理1： 单调有界数列必有极限[1]

利用单调有界数列收敛定理时，其难点有时在于单调性的证明，有时在于估计有界性，二者都常用数学归纳法。

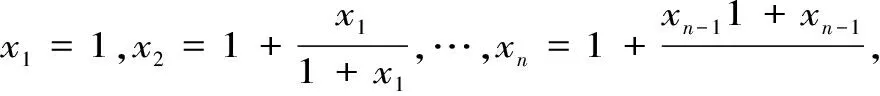
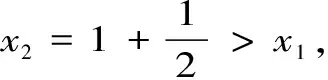
所以，数列{xn}有界。由单调有界数列收敛定理得，数列{xn}收敛。

1.3　利用柯西收敛准则

定理2：[1](柯西收敛准则)数列{xn}有极限的充要条件是：对任意给定的ε>0，有一正整数N，当m，n>N时，有|xm-xn|<ε

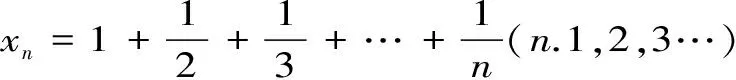
证明{xn}是发散的。

证明：根据柯西收敛准则，只须证明∃ε0>0，对

∀N(自然数)，∃m,n>N时，有|xm-xn|≥ε0，在本题中对任意正整数n，取m=2n，有：

因此，{xn}是发散的。

1.4　利用数列子列的性质

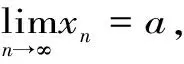
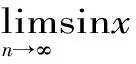
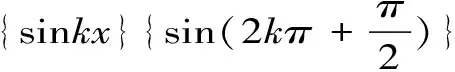
1.5　利用海涅定理判断极限的收敛性

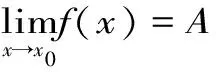
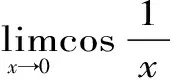
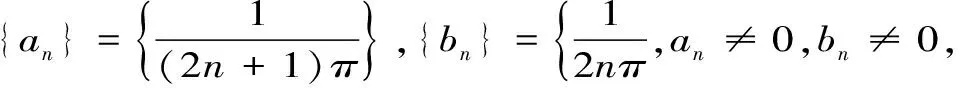
1.6　利用上、下限相等

因为任何有界数列必存在有穷的上、下限，而数列收敛的充要条件又是上、下限相等[1]，所以在已知数列不具有单调性或不易估计它能否满足柯西收敛准则的条件时，常常从上极限大于下极限或下极限不小于上极限入手来证明收敛性；或者从上、下极限不相等来证明数列发散。

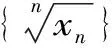
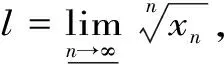
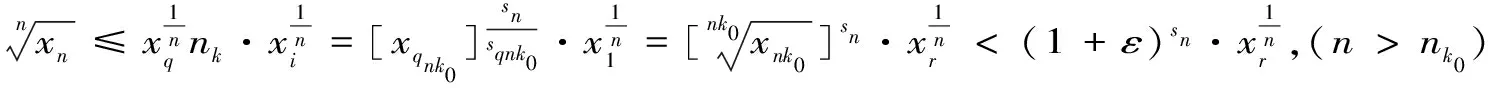
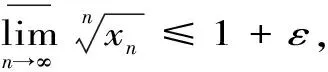
1.7　利用施笃兹定理

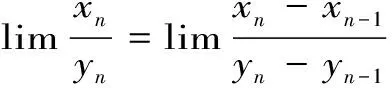
例8：设x1∈(0,1)，xn+1=xn(1-xn)(n=1，2，3，…)，证明数列{xn}是收敛的。

故根据施笃兹定理，得：

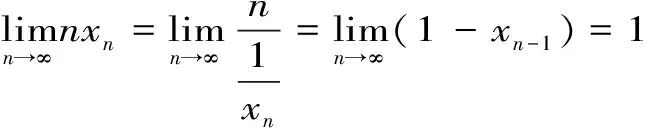
1.8　利用构造法

构造一个新的便于研究的数列，把它作为桥梁来研究原数列，这也是数学上常用的方法之一。

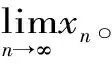
证明：设yn=xn-1，则yn=sinyn-1(n=1,2,3,…)

因为：-1≤sinx≤1,y0=-1所以：-1≤yn=sinyn-1<0

yn-1≤sinyn-1=yn(n=1,2,3…)故{yn}单调增加且有上界，所以数列{yn}收敛。

2　结　语

由于极限理论在数学分析中占有十分重要的地位，极限存在性的证明与方法有许多种，本文概述的九种证明方法仅是主要的几种，绝不是其全部方法。从以上方法中可以看到，只要灵活地加以综合运用，就能有效地解决不同形式的极限存在性证明问题。

参考文献：

[1] 陈传璋,金福临,朱学炎,等.数学分析[M].北京:高等教育出版社,1992：29,55,43,104-105,59,81-84.

[2] 刘玉琏,杨奎元,吕凤.数学分析讲义学习指导书[M].北京:高等教育出版社,1988:38,95,46.

[3] 李心灿,宋瑞霞,唐旭晖,等.高等数学专题十二讲[M].北京：化学出版社，2001:51.

[4] 菲赫金哥尔茨.微积分学教程(第一卷第一分册)[M]. 北京:人民教育出版社,1980:59-60.