基于标志点的三维数据拼接方法研究

秦绪红，赵杰，程俊廷

(1.辽宁石油化工大学，辽宁 抚顺 113001;2.黑龙江科技学院，黑龙江 哈尔滨 150027)

0 引言

逆向工程(reverse engineering)是利用电子仪器采集被测物体表面的原始数据，然后再利用相关软件计算出所采集数据的空间坐标，其主要任务是将原始物理模型转化为工程设计概念或产品数字化模型。数据拼接是逆向工程中的研究难点之一，对完善测量数据到曲面重构的各个环节都有着极其重要的意义。其目的是把两片或多片数据点云按正确的关系排列，拼合成一片完整的数据点云［1-2］，也就是把不同的坐标系下测得的数据点云进行坐标变换，问题的关键是坐标变换参数R(旋转矩阵)和T(平移矢量)的求取［3］。

多视点云拼接是计算机视觉和图形图像处理领域重要的研究方向，广泛应用于计算机辅助设计、虚拟现实、飞机制造、医学影像等领域。三维物体的复杂多样性和测量系统得到点云的海量散乱性是三维拼接的一个难点。

1 基于标志点的拼接

在对物体进行三维测量的过程中，为了将从不同视场扫描得到的点云数据整合到统一的坐标系下，需要对其进行刚体变换。在实际测量中，引入人工标志特征进行辅助拼接。引入的标志点是人为制作的图形特征点，将其贴于物体表面，通过检测可以得到若干标志点在不同视角下的三维坐标。由标志点的空间几何不变性，得到不同标志点在不同视角下的匹配关系［4］。根据已获得的若干标志点的匹配关系，来求解不同视场下的坐标系关系，进而对全部三维数据进行配准。此方法方便灵活，容易操作，且具有良好的鲁棒性。

将标志点贴于被测物体表面是在扫描之前要做的一项至关重要的工作。标志点以最小20 mm 的距离随机地粘贴于被测表面。如果表面曲率变化比较小，距离可达到100 mm。这些标志点使得系统可以在空间中完成自定位。定位点粘贴时需离开边缘12 mm 以上(图1)。

1.1 采用ICP 算法

国内外现有的多视点云拼接方法大多都是在Besl 和Mckay 提出的ICP(iterative closest point)方法［5］的基础上发展和改进而来的。迭代最近点法ICP 经过了十几年的发展，并得到了不断地补充和完善［6-7］。在ICP 算法中，对于待拼接的2 片点云(P，Q)，首先根据一定的准则确立对应点集P 与Q，其中对应点对的个数为n。然后通过使用最小二乘法迭代，计算出最优的坐标变换，即旋转矩阵R和平移矢量T，使得误差函数最小。

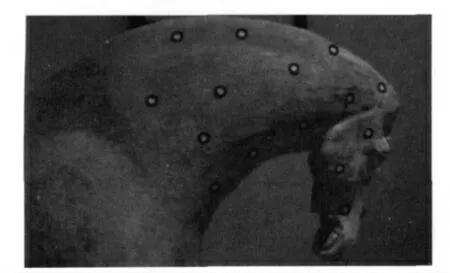
图1 贴圆形标志点的物体

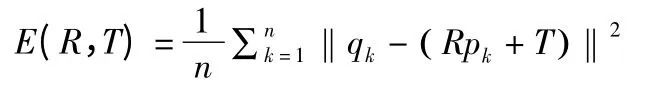
给定的初始变换估计以及在迭代过程中确立的对应关系在很大程度上决定了ICP 算法的运行速度和全局最优的收敛性。各种粗拼接技术可为ICP 算法提供较好的初始位置，所以迭代过程中确立正确的对应点集以避免迭代陷入局部极值成为各种改进算法的关键，决定了算法的收敛速度与最终的拼接精度。

1.2 SVD 算法

为了实现局部扫描点云所处坐标系与空间框架所处坐标的转换，与ICP 算法相同，SVD 算法也需要求解坐标变换参数R 和T。若已经得到两个不同视下的特征匹配点对是P={pi|pi∈P，i=1，2，…，n}和Q={qi|qi∈Q，i=1，2，…，n}，pi和qi和均为3×3 的相量，则所求解旋转矩阵R 和平移矢量T，应使下面的目标函数最小。

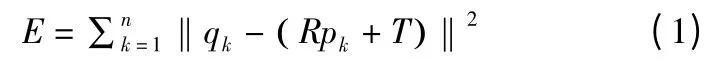
采用SVD 分解法［8］，具体步骤如下所示:

1)对于空间点集{pi|pi∈P，i=1，2，…，n}和{qi|qi∈Q，i=1，2，…，n}分别计算p 和q，(其中p=;q=)。

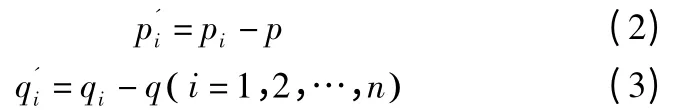
3)由式(1)，(2)，(3)可得:

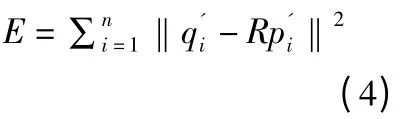
4)对于式(4)采用SVD 矩阵分解法得到R

5)求解平移向量T :

求出旋转矩阵R 和平移向量T 后对点Q 中的任意一点q，可由式(6)求得点转换到点集P 坐标系下的对应点，进而实现数据的拼接。

1.3 四元数法

由Horn［9］提出的四元数法是利用两组相互之间一一对应的三维坐标点集{pi}，{qi}以便求解两组三维点集之间的坐标旋转R 和平移矩阵T，定义四元数q=［q0，q1，q2，q3］，应用四元数法则3×3 旋转矩阵R(q)可表示为:

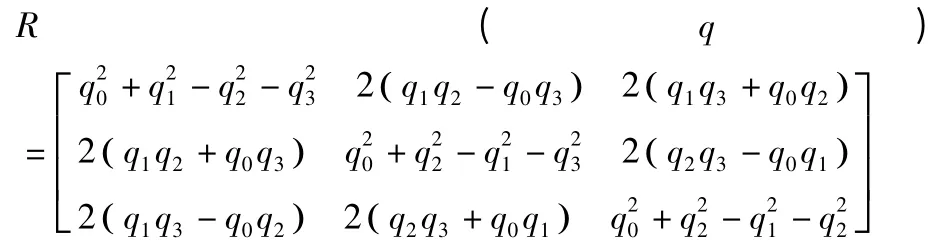
1)平移矩阵:T(q)=μp－R(q)μx(μp:参考点集{pi}的中心矢量，μx:参考点集{qi}的中心矢量);对各自质心平移三维点集 {pi}，{qi}，得到点集。

2 拼接实例与结果

首先用ZEISS CONTURA SELECT 三坐标测量仪(精度:2.3+L/300 μm)测出两球心间距离(S=999.780 mm)。为保证拼接时相邻区域公共标志点数不少于三个，对双球长杆进行分区域测量(本实验将被测物从左到右分五个区域测量)(图2)。

图2 单次测量结果

将ICP，SVD 和四元数法拼合后的结果分别用Geomagic Studio 逆向软件对其进行球心距测量(图3)。

图3 拼合后结果

测量结果证明:虽然ICP 参与计算的数据量比较大，但其拼接精度较高;SVD 和四元数算法精度相当，因而采用ICP 算法对双球长杆的球心距进行拼接精度测量。多次测量数据(保留小数点后三位有效数字)如表1 所示:

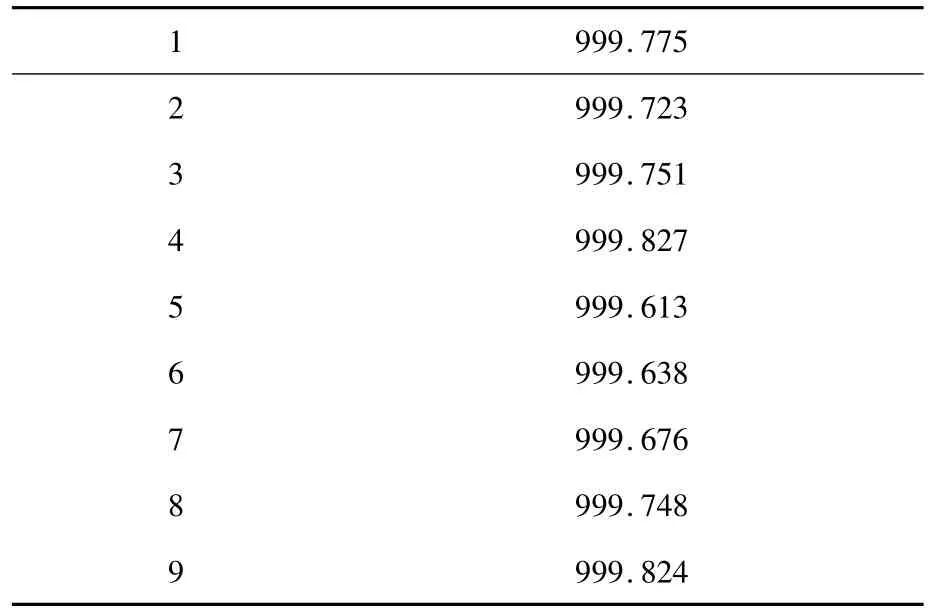
表1 采用ICP 算法的多次测差数据

此方法能够较好地实现测量数据的拼接，拼接误差在空间上分布较均匀，其精度完全可以满足实际的需求，且测量范围不受限制，具有较好的曲面特性，对后续的物体曲面建模提供便利，同时也适用于大型物体的测量。

3 结论

本文探讨了基于标志点的三维物体拼接技术。在获得物体不同视角下三维点云数据的基础上，对ICP，SVD和四元数法的点云拼接技术进行了实验分析。实验结果证明:ICP 法能较好地实现大型物体的三维数据拼接，精度较高，非常适用于实际应用。

［1］谢光辉，孙军华，杨珍.一种自由曲面视觉测量三维数据拼接方法［J］.北京航空航天大学学报，2009，35(7):877-811.

［2］欧阳祥波，宗志坚，熊会元.基于标志点的测量数据自动拼接方法［J］.中国图象图形学报，2008，13(2):298-301.

［3］雷家勇.逆向工程中三维点云拼接系统的研究与实现［D］.南京:东南大学，2005.

［4］梁云波，邓文怡，娄小平.基于标志点的多视三维数据自动拼接方法［J］.北京信息科技大学学报(自然科学版)，2010，25(1):30-34.

［5］Paul J Besl，Neil D McKay.A Method for Registration of 3-D Shapes［J］.IEEE Trans on Pat，Anal and Mach Intel，1992，14(2):239-256.

［6］解则晓，徐尚.三维点云数据拼接中ICP 及其改进算法综述［J］.中国海洋大学学报，2010，40(1):99-103.

［7］戴静兰，陈志杨，叶修梓.ICP 算法在点云配准中的应用［J］.中国图像图形学报，2007，12(3):517-521.

［8］王宫，钟约先.大面积形体三维测量数据拼接技术的研究［J］.机械设计与制造，2007(9):90-92.

［9］Horn B K P.Closed-form solution of absolute Orientation using quite quaternion［J］.Journal the Optical of Society American A:Optics Image Science and Vision，1987，4(4):629-642.