基于线性调频扩频定位的动态误差修正算法

席通专，丁希仑

（北京航空航天大学机械工程及自动化学院，北京 100191）

0 引言

随着无线传感器网络技术的发展，其低成本、低能量消耗、多功能［1］等特点吸引了大量研究，已经被广泛应用于物联网、人员定位、机器人定位等众多领域。定位功能是无线传感器网络的一大特点，与传统定位技术相比有组网灵活、成本低等特点。本文所采用的线性调频扩频技术（chirp spread spectrum，CSS）是基于IEEE802.15.4a的物理层标准的无线传感器技术，在中短距离内具有良好的定位精度和稳定性。

CSS技术是基于信号传播时间（TOA）的测距，获得节点之间的距离值后，可以采用无线传感器网络中常用的基于距离的定位算法进行定位。目前CSS定位的误差修正主要研究CSS传感器本身结构特点和底层协议来提高测距精度，结合多个测距信息来反馈修正误差的研究不多，这样可以使测量距离得到相互修正。近年来，Ming Cao等人在文献［2，3］中把Cayley-Menger行列式［4］引入定位中，推导出了平面定位误差满足的二次约束方程，这对定位误差修正研究意义重大。利用误差的距离几何约束方程来对误差进行最优估计的研究进展却不多。Ming Cao提出了一种基于距离几何约束方程转化为求误差平方和的最值问题来估计测量误差。文献［5，6］中，在不同定位系统中应用Ming Cao提出的方法来进行测距误差修正，再结合定位算法来提高定位精度，并进行了仿真分析验证。他们的研究仅采用仿真方法对算法进行验证，没有进行定位实验评估算法效果，本文通过分析Ming Cao的基于距离几何约束的误差平方和最小值来估计误差的方法后，发现该方法对定位精度的改善并不明显，本文实验也证明了这点。

根据上述分析，本文提出了一种结合测距误差模型与距离几何约束方程来对视距环境下0定位进行距离修正，给出实际定位中每个位置点的最优测距误差模型，再用这个系数在一定范围内变化的线性方程对测量值进行动态修正。文章第1节分析了视距环境下CSS测距误差模型特性，第2节介绍了距离几何约束方程，分析Ming Cao的误差平方和最优解问题来修正误差算法，然后提出了结合测距误差模型和距离几何约束的动态修正算法，文章最后部分通过室内CSS定位实验比较了动态修正算法、Ming Cao的距离几何约束算法及普通静态修正算法的效果。

1 CSS测距误差模型分析

线性调频扩频技术以前主要用于脉冲压缩雷达，能够很好地解决冲击雷达系统测距长度和测距精度不能同时优化的矛盾。IEEE将CSS技术列为802.15.4a技术标准的底层实现方式之一之后，CSS技术被越来越多被用于无线定位。CSS系统通过测量信号传播的时间来计算距离，采用一种对称双向两次测量法（SDS-TWR）［7］。该方法不需要节点之间时钟同步即可完成测量，减少时钟漂移带来的误差。CSS定位系统测距精度虽然比其他的无线传感器网络高，但测量距离也包含了噪声和误差。误差主要来源于两部分，定位系统自身所引起的误差和外部环境引起的误差。CSS自身所引起的误差为系统性误差，主要是由传感器的自身所有的参数如时钟精确性、天线性能等导致的偏移距离。同时系统还存在由于非视距、多经效应和具体环境特点带来的误差，非视距环境会导致CSS系统出现比较大的误差。由于本定位系统所应用的环境特点，研究视距范围内的误差修正，本文所提出的方法在非视距环境下并不能保证良好性能。

在视距环境下，CSS系统测距模型大致满足线性关系，模型的系数与测距传感器本身参数和环境有关，先通过测距测试研究CSS系统在视距环境的测距模型。测试分为两组，一组研究同一对测距模块在不同环境下的测距误差模型，一组研究两对不同测距模块在相同环境的测距误差模型。

测试1:选择一对测距模块，固定其中一模块，另一个模块依次放置在设定距离点测量;在室内不同位置环境重复上述测试。

测试2:选择两对测距模块，每一对测距模块在同一位置环境按照实验1测距方法进行测量。

得到测试结果后，通过最小二乘拟合得到相应的测距误差模型，数据点及拟和曲线如图1所示，（a）、（b）为测试1结果，（c）、（d）为测试2研究结果，拟合方程如下:

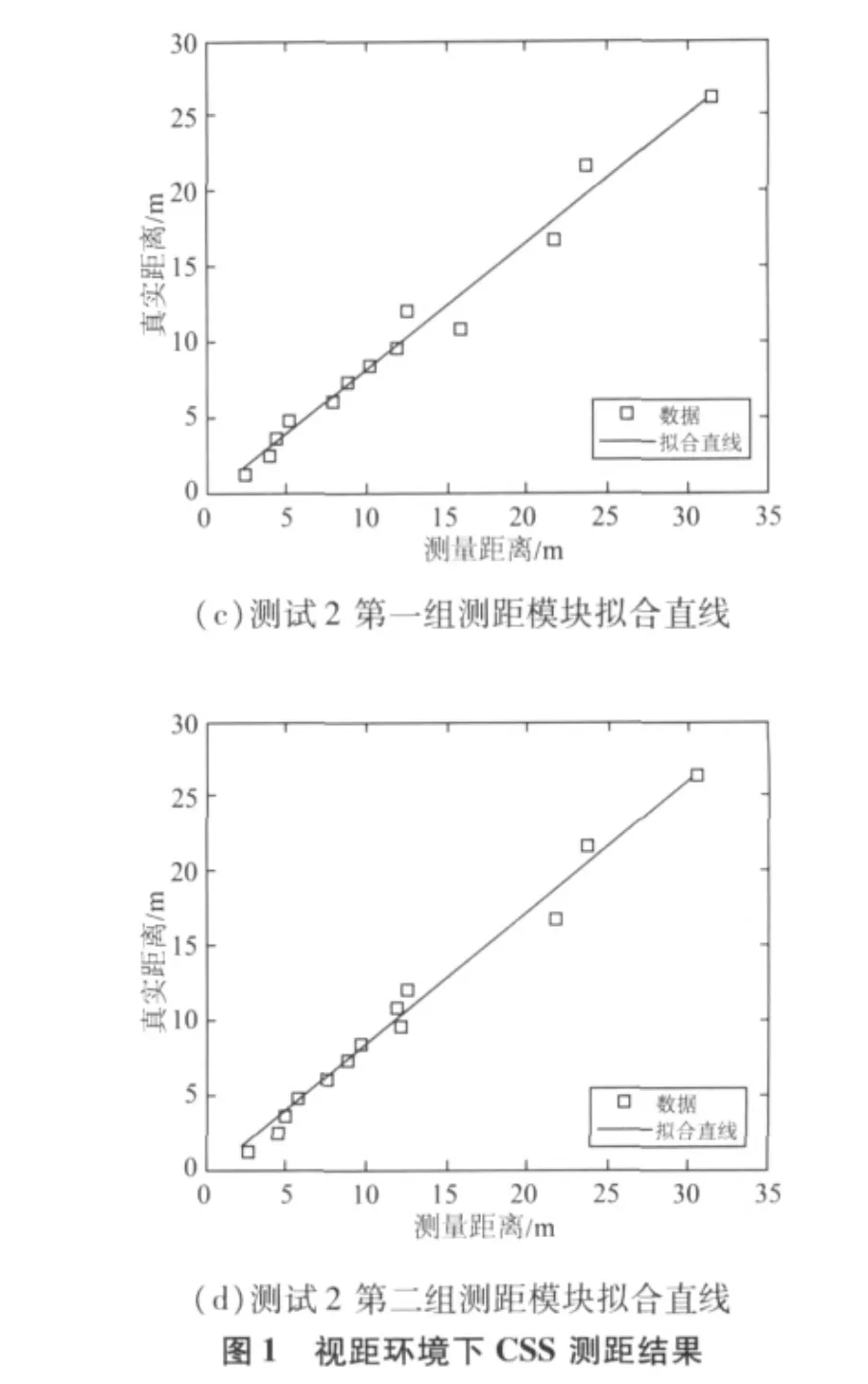
上面的测试结果验证了存在误差和其他干扰的CSS测距模型线性关系的系数并不是固定的，环境的变化、节点的不同，甚至测距模块的姿态变化，都会引起测距模型系数的变化。如果有非视距或其他多径效应存在，测量距离与真实距离可能不满足线性关系，或者拟合直线的系数会变动很大，此时拟合方程式没有意义。因此，视距环境下的CSS定位中有以下测距误差模型为:

其中:d是真实距离;d是测量距离;a，b为线性方程系数。其中a1，a2，b1，b2可以根据定位前对定位模块进行测距测试拟合所得系数平均值附近的一个较小区间。如果拟合系数超过所取范围，则认为有较大噪声干扰，仍然认为测距误差模型在式（5）的范围内。

目前视距范围内减少误差的方法一般是取测距测试所拟合的测距误差模型方程作为修正方程对测量结果进行修正，即在整个定位中不考虑节点之间的差异、环境特点等导致测距误差模型方程的差异，而采用同一方程对结果进行修正，本文中把这种方法叫做静态误差修正算法，研究根据每个定位最小单位（三个锚节点，一个待测节点，如图2所示）内利用三个测量距离，然后通过距离几何约束寻找最优的测距模型方程d=a*d+b*，最大限度地动态修正误差，第2节详细介绍了误差修正过程。

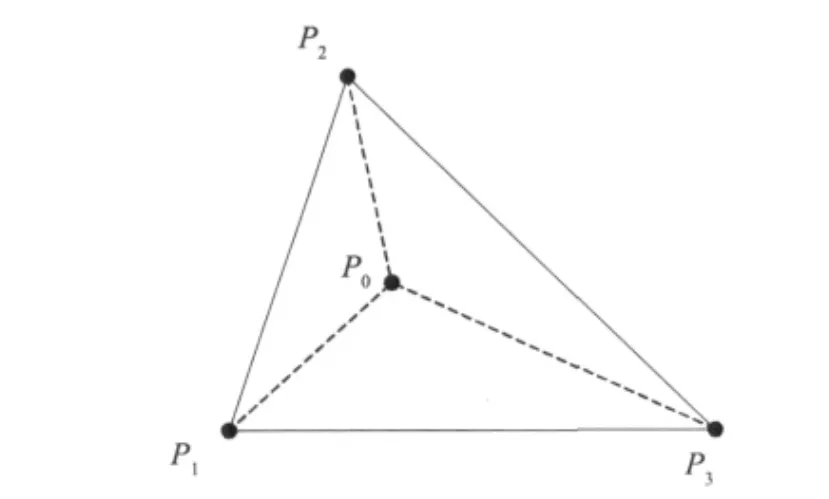
图2 三个锚节点定位示意图

2 距离几何约束及动态误差修正算法

2.1 Cayley-Menger行列式及距离几何约束修正误差法分析

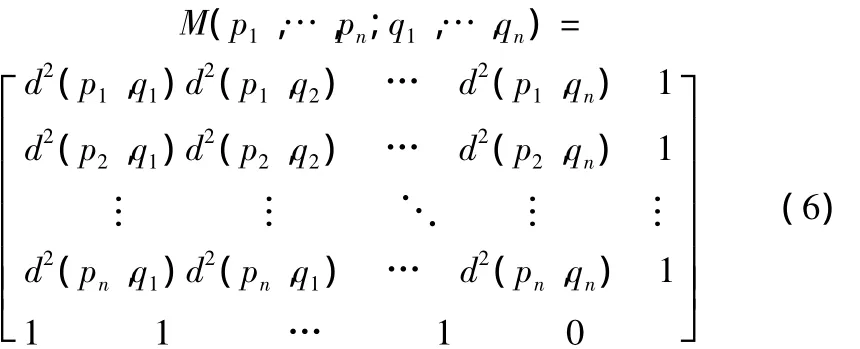
式中d（pi，qj）表示点pi和qj之间的欧几里得距离。两个点序列的Cayley-Menger双联行列式［4］定义为:

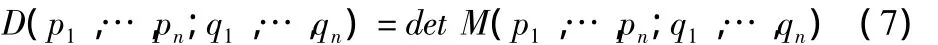
当两个点序列是同一序列时，用D（p1，…，pn）表示D（p1，…，pn;q1，…，qn）用 M（p1，…pn）表示 M（p1，…，pn;q1，…，qn）并把 D（p1，…，pn）叫做 Cayley-Menger行列式。

Cayley-Menger行列式有下面比较经典的结论:

定理1.（距离几何基本定理）考虑m维空间由点p1，…，pn组成的n元组。如果n≥m+2，则Cayley-Menger矩阵M（p1，…，pn）是奇异的，即:

图2为基于距离定位的一个常用最小定位单位，其中已知三个锚节点1，2，3的位置坐标，由无线传感器可以测得待测节点0到锚节点1，2，3的之间距离。待测节点0到锚节点1，2，3，4的测量距离记为，i=1，2，3;4个节点之间的实际欧式距离记为 dij=d（pi，pi），i，j=0，1，2，3＆i≠j。定义测量误差 εi为:

则由定理1 知，D（p0，p1，p2，p3）=0，联立D（p1，p2，p3）≠0，Ming Cao等人在文献［2，3］中推出以下误差关系式:

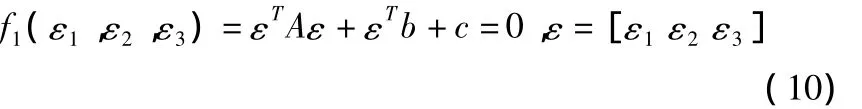
其中:A是3×3阶矩阵，b是3×1阶矩阵，c是一实数，且A，b，c是由dij表达的。可以看出式（10）是仅关于三个误差值的一个约束方程。

在此基础上，Ming Cao等提出了基于距离几何约束方程的误差估计方法。通过一个最小二乘法问题来求解最优值来估计误差如式（11）所示，本文中把这种方法叫做距离几何约束Ming Cao修正法。

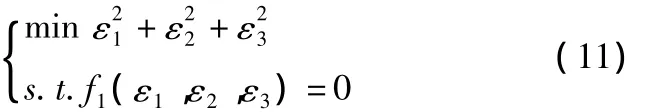
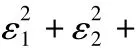
为了解决上述问题，下面部分根据CSS测距特点提出了误差动态修正方法，充分利用了距离几何约束方程把测量距离误差建立联系并达到相互修正的作用。

2.2 基于距离几何约束方程的动态误差修正算法

对于CSS定位系统来说，如第1节分析，视距环境下CSS测量距离非严格满足线性关系，且线性方程的系数也随着不同测距模块、测距环境等在一个范围内变化。实际定位中定位节点数量众多，不可能提前测试好每对节点之间的测距误差模型系数，即使能测也是没有意义的，因为测量过程中测距模块的位置、位姿、信道等变化都会引起系数变化。

目前针对上述问题的处理方法多采用如第1节所述静态修正算法。但是这种修正方法有明显不足，CSS测距系统是一种高精度的系统，在100 m范围内测距误差仅仅2～3 m，而测距误差模型修正的距离是同一个数量级数据，采用不准确测距模型方程修正后误差依然可能很大。因此采用更准确的测距误差模型是很必要的，最好的解决方法是能估计出最小定位单位中待测节点与三个锚节点的三个测距误差模型，但是由于约束方程数目不够求解出每个模型系数。本算法则假设最小定位单位中三个测距误差模型为同一模型，然后再根据距离几何约束条件找出这一最佳估计。在本算法中，把使得距离约束方程f1（ε1，ε2，ε3）取得最接近0的系数作为一个最小定位单位的最佳测距误差模型。满足距离几何约束为0的测距误差模型可能有多个，但是根据第1节研究，视距环境下的测距误差模型系数一般在一个范围内，而把超出这个范围系数的测距误差模型认为是其他较大随机误差或非视距等引起的，或是数学方法求出的无效解。研究中只考虑在已知系数范围内使距离约束方程左边最接近0的一组系数解为最佳测距误差模型的系数。

根据第一节的研究，根据定位实验前测距实验拟合测量模型方程，选取多个拟合测距误差模型系数的平均值作为中位置，然后选择中位置附近的一个区间 a∈［a1，a2］，b∈［b1，b2］作为求解最佳测距误差模型系数区间。联立

式（5）和式（9）得到以下方程组，

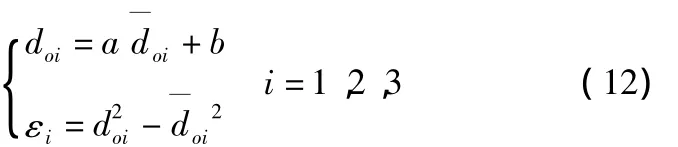
由式（12）可以推出:

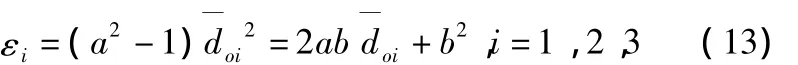
把εi带入距离几何约束方程式（10），得到关于未知数a，b的函数，记为

在 a∈［a1，a2］，b∈［b1，b2］内 F（ab）最接近 0 所对应的一组a*，b*就是测距误差模型的最佳系数估计.因此求解最佳测距误差模型方程的问题就转化为如式（15）的一个最优值求解的问题，

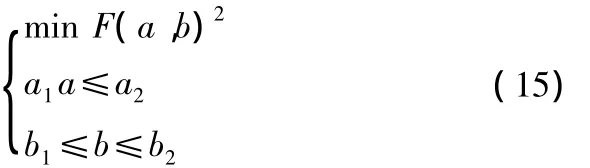
通过数值方法可以求解出系数的最优估计:a*，b*。求解出最佳测距误差模型d=a*+b*后，利用这个模型对测量距离进行修正，修正后的距离采用平面定位方法如三边法等即可求得待测节点位置坐标。动态误差修正算法的意义在于能够更准确的修正测量距离，修正后的距离再采用任何其他定位算法都提高定位精度，但是本算法相对于静态修正算法增加了计算量。

3 实验及结果分析

3.1 实验设计

本定位实验采取Nanotron公司开发的CSS测距模块。实验场地为室内15.2 m×15.2 m的空间，中间无障碍物，测距模块安装在1.5 m等高的支架上，三个锚节点位于P1（0.95，0.95），P2（14.25，14.25），P3（14.25，14.25），定位位置如图3所示的25个点上，图中每格距离为1.9 m。待定位节点依次放置在这25个位置上。

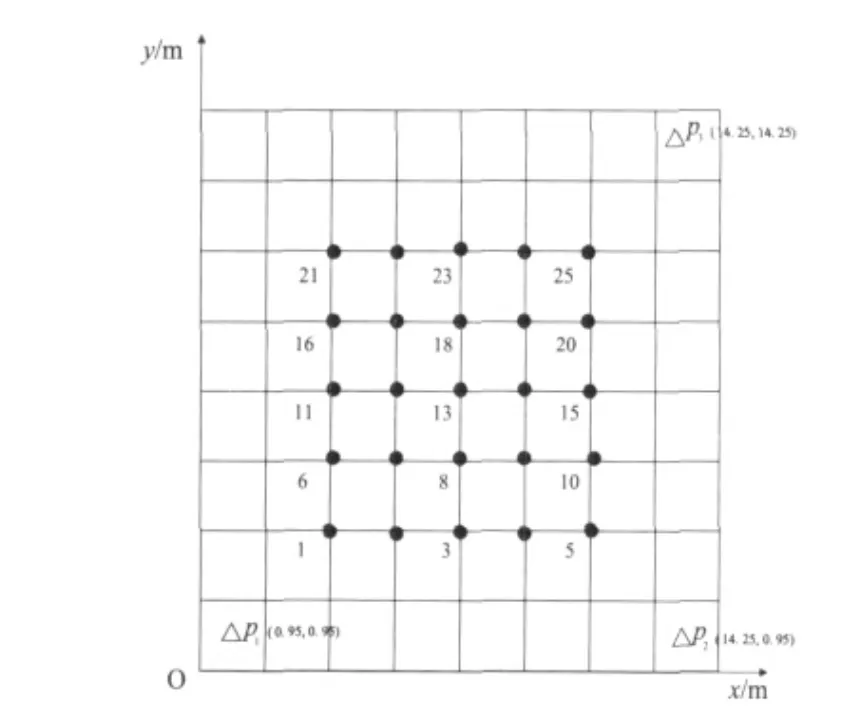
图3 定位实验布置图

3.2 实验结果分析

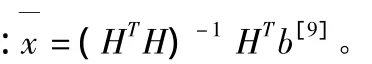
用式（16）作为定位误差来评价三种定位算法效果:

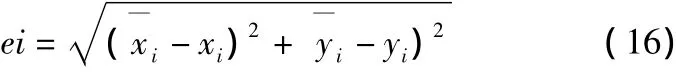
图4 定位误差对比图

从图4可以看出，本文所用方法在92% 的点比距离几何约束Ming Cao法和静态修正法有明显精度改善，距离几何约束Ming Cao修正法与静态修正法效果近似。定位误差去掉最大3个点和最小3个点计算出三种方法的误差值的平均值。通过表1中可以看出动态修正法的三项误差指标都远远优于距离几何约束Ming Cao修正法和静态修正法，动态修正的误差是静态修正法误差的61%，距离几何约束Ming Cao修正法的68% 。由此可得，本文所用误差动态修正方法大幅提高了定位精度。同时，本文所用方法修正的测量距离可以与其他定位精度更高的基于距离的定位算法结合，将能进一步提高定位算法的精度。

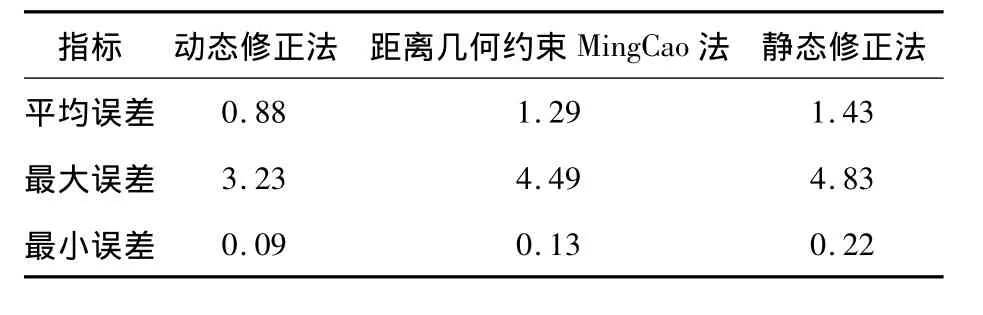
表1 实验指标对比

4 结论

CSS定位系统具有良好的视距环境下定位精度。距离几何约束方程准确地描述了平面定位中误差之间关系，能够用于测量距离误差修正。本文所提出的结合测距误差模型与距离几何约束方程的动态修正算法能有效地修正视距环境下CSS定位系统测量误差提高定位精度，效果好于其他常用方法。

［1］G.Mao，B.Fidan，B.D.O.Anderson.Wireless Sensor Network Localization Techniques［J］.Computer Networks，2007，Volume 51，Issue 10，Pages2529-2553.

［2］M.Cao，B.Anderson，A.Morse.Localization with imprecise distance information in sensor networks［J］.44th IEEE Conference on Decision and Control，and the European Control Conference，2005，pp.2829-2834.

［3］M.Cao，B.Anderson，A.Morse.Sensor network localization with imprecise distances［J］.Systems ＆ Control Letters，2006，pp.887-893.

［4］G.M.Crippen，T.F.Havel，Distance Geometry and Molecular Conformation［M］.Wiley，New York，1988.

［5］J.Zheng，C.Wu，H，Chu.Localization algorithm based on RSSI and distance geometry constrain for wireless sensor network［J］.Electrical and Control Engineering（ICECE），2010 International Conference on，2010，2836-2839.

［6］朱建新，高蕾娜，张新访.基于距离几何约束的二次加权质心定位算法［J］.计算机应用，2009，29（2）.

［7］IEEE Standard，IEEE Std 802.15.4a，Aug.2007.

［8］Leonard M.Blumenthal.Theory and Application of Distance Geometry［M］.Oxford:Oxford University，1953.

［9］A.H.Sayed and N.R.Yousef，"Wireless location，"in Wiley Encyclopedia of Telecommunications， J. Proakis， Ed. New York:Wiley，2003.