基于Lp范数的2DPCA的人脸识别方法

李 勇，梁志贞，夏士雄

LI Yong,LIANG Zhizhen,XIA Shixiong

中国矿业大学 计算机科学与技术学院，江苏 徐州 221116

School of Computer Science and Technology,China University of Mining and Technology,Xuzhou,Jiangsu 221116,China

1 引言

在大规模的数据分析问题中，高维的特征向量会造成高维协方差矩阵奇异性问题，从而使问题的解决变得困难，因此降维是非常重要的。要求它在不降低性能表现的前提下，通过降低特征向量的维数来简化问题。主成分分析（PCA）[1]就是一种常用的降维方法，它常用一组向量来最大限度地表示所给的数据。这些向量组成了一个低维的线性子空间，通过这个子空间，可以有效地获取原始输入空间中的数据的内在结构。

由于PCA是基于图像向量的方法，所以它在降低特征维数时，比不上直接基于两维图像矩阵的方法方便。1993年Liu等人提出利用数字图像矩阵直接构造图像散布矩阵，并在此基础上进行鉴别分析的新方法[2]；2003年Yang改进了Liu的方法[3]，得到一种具有统计不相关性的图像投影鉴别分析方法；2004年Yang等人[4]将文献[3]的方法用于图像重构，取得了很好的效果。

由于在PCA和2DPCA[4]中的目标函数都运用了L2范数，所以异常值的出现会因L2范数的使用而被扩大，所以这种方法对异常值较敏感。为了减轻这个问题的影响并且取得更好的稳定性，许多人做了相关的研究[5-9]，在文献[7]中，改进了以往的L1-PCA算法，并取得了不错的效果。在文献[8]中，改进了基于L2范数的传统的2DPCA，提出了基于L1范数的2DPCA（2DPCA-L1）方法。

本文对2DPCA-L1方法进行了改进和推广，提出了基于L1范数且受Lp范数约束的2DPCA方法（2DPCA-Lp），其主要思路是直接对图像矩阵进行操作，目标函数仍采用L1范数，而在求投影向量时，使用Lp范数进行约束。其特点为：它通过引入参数p控制投影向量的稀疏性，从而用不同的p值来处理不同的情况，提高识别率和鲁棒性。

2 2DPCA与2DPCA-L1

这章简要介绍了2DPCA和2DPCA-L1这两种方法。它们都是直接处理图像数据的方法。

2.1 2DPCA方法

2DPCA是图像矩阵的子空间学习方法。与PCA相比，2DPCA能够获取更多的子空间信息，从而有利于图像的分类或者重建。如果设列投影向量x∈ℜn，2DPCA的思想是将m×n的图像矩阵A通过线性变换Y=Ax投影到x上，从而可以得到图像 A的特征投影向量Y∈ℜm×1。设训练样本为 A1，A2，…，AN∈ℜm×n，其图像的总体散布矩阵C定义为：

在2DPCA中，需要找到一组最优投影矩阵U=[x1，x2，…，xd]∈ℜn×d，使得准则函数最大化：

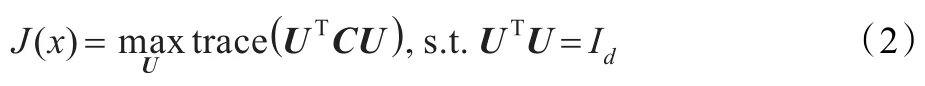
此时，各个图像矩阵在U上投影后所得特征向量的总体散布的程度最大。最优投影向量组 x1，x2，…，xd为C的d个最大特征值所对应的标准正交的特征向量。

2.2 2DPCA-L1

在2DPCA-L1方法中，设列向量 x∈ℜn×1为第一个主成分向量。对于N个训练样本图像，Ai∈ℜm×n，i=1，2，…，N，其对应的特征Yi∈ℜm为：

其中 Aij∈ℜ1×n为 Ai的第 j行。

2DPCA-L1是在低维特征空间中，找到向量x使得如下函数取得最大值：

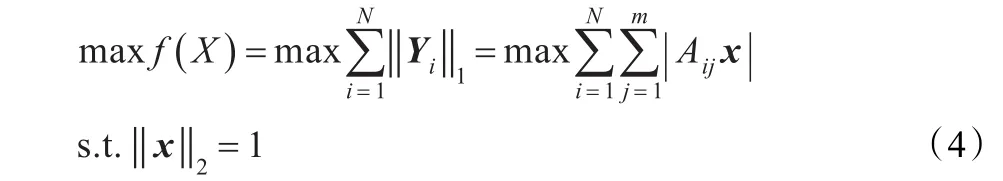
其中 ‖·‖1和 ‖·‖2分别表示 L1 范数和 L2 范数。注意到利用这个方法只能得到一个投影向量，为了取得多个投影向量，文献[8]中的作者利用了贪婪算法。

3 2DPCA-Lp方法

3.1 模型及算法

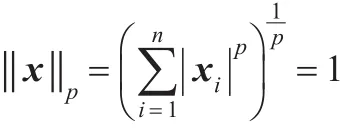
同样，设第 i幅图像 Ai∈ℜm×n，其对应的特征向量Bi∈ℜm×1：

其中，Aij∈ℜ1×n为图像 Ai的第 j行。

2DPCA-Lp的优化问题是在低维特征空间中寻求投影向量x使得下式取得最大值，即

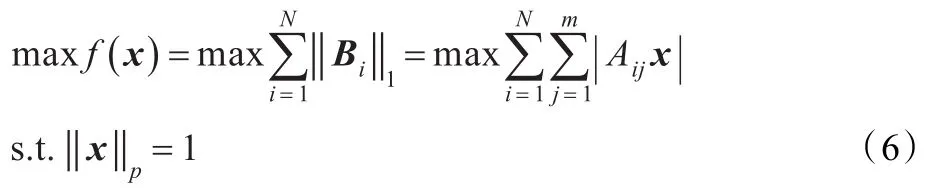
下面，首先给出算法求解式（6）。类似于文献[8]中的算法，给出算法1来求解式（6）。

算法1 2DPCA-Lp

（1）初始化：选择任意的 x(0)，令 x(0)←x(0)/‖x(0)‖p，t=0。

（2）极性检测：对于所有的 i∈{1，2，…，N}，j∈{1，2，…，m}，当 Aijx(t)＜0，pij(t)=-1，否则 pij(t)=1。

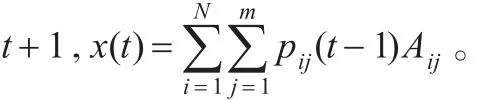
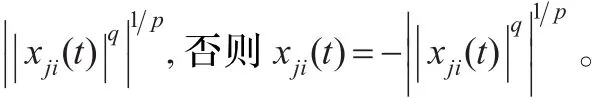
（4）收敛检查：

①如果 x(t)≠x(t-1)，执行（2）。

②否则，令x*=x(t)并结束算法。

为了分析算法，首先介绍了霍尔德不等式[10]。当 p，q∈(1，∞)，且1/p+1/q=1时，在 n 维欧式空间中，对于所有的(x1，x2，…，xn)，(y1，y2，…，yn)∈ℜn，有如下不等式成立：

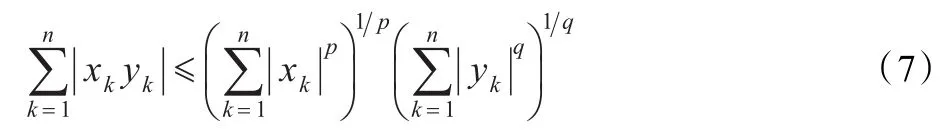
等号成立当且仅当|xk|p与|yk|p成比例时成立。

既然该算法是一种迭代方法，下面给出定理1来表明算法1的局部收敛性。

定理1由算法1得到的向量收敛于局部最大值。

证明 首先，由算法1的（2）和（3）得到：

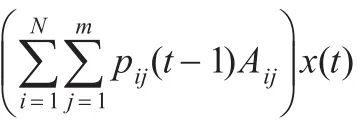
3.2 选取多个关联特征（k＞1）

注意到通过式（6）只能取得一个最佳投影向量x。但是在实际情况下，仅仅利用一个投影向量是不合适的，往往经常需要多个投影向量，为了取得多个投影向量，采用类似献[8]中的贪婪算法，描述如下：

在文献[8]中，由于在约束集中采用了L2范数，容易证得取得的xt与xt-1是正交的。而本文的方法采用Lp范数，所以通常所取得的xt与xt-1并不正交。注意到2DPCA-Lp方法仅仅取得局部最优值。很显然当 p=2时，本文的方法就退化为2DPCA-L1方法。另外，由于采用多次赋给不同初始的值来选取目标函数的最大值，所以使得该方法取得全局最大值的可能性就较大。

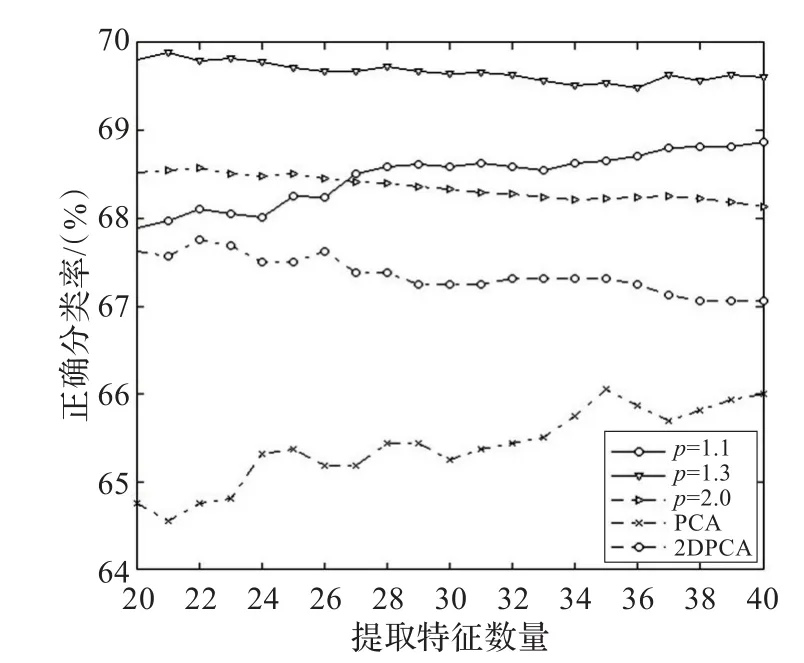
图1 在ORL数据集上性能的比较

4 实验结果与分析

4.1 ORL数据库

ORL人脸数据库由40个人、每人10幅，分辨率为112×92的人脸图像组成，这样总共400幅图像。样本包含着不同姿态，不同光照和不同面部细节的人脸图像。首先测试了2DPCA-Lp，PCA，2DPCA方法在ORL人脸数据库中的性能。对于2DPCA-Lp方法在求训练样本的特征时，需要先把训练样本中值化。令p={1.1，1.2，…，2.0}，其中当p=2.0时，2DPCA-Lp方法就退化成2DPCA-L1方法[8]。对于每类样本，随机选取其中的20%作为训练集，80%作为测试集进行交叉验证实验，提取特征数量为20至40并采用最小距离分类器进行分类，部分实验结果如图1所示。表1也列出了每种方法的最好性能以及取得最好性能所对应的提取特征数量。另外，在实验的图像上加入了8×8的遮挡块，从而进一步测试这几种方法在遮挡情况下的性能，实验结果如图2所示，各种方法的最佳识别率如表1所示。

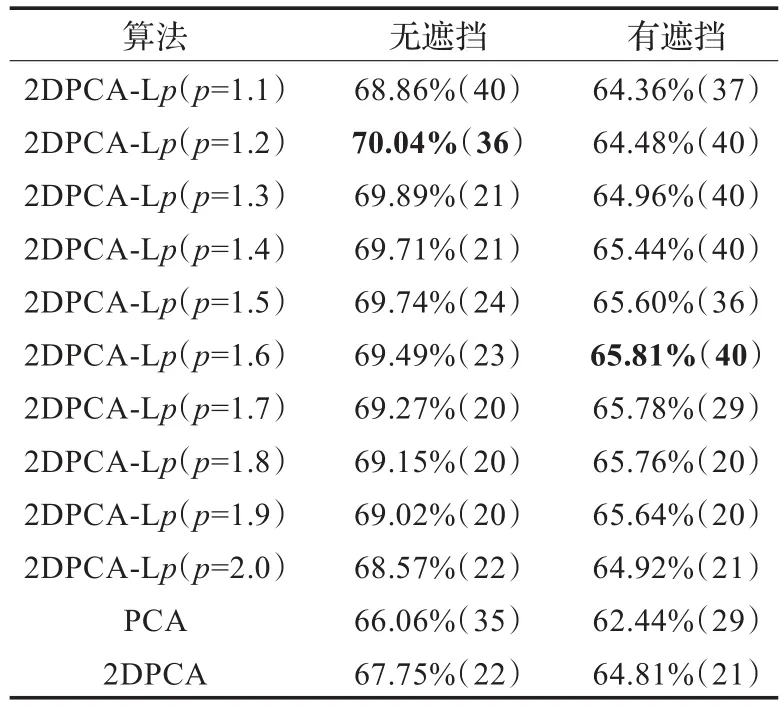
表1 ORL上的最优分类率及对应的提取特征数量

从图1可以看出，p=1.2时识别率比其他方法都要高，所以在图像没有遮挡的条件下，本文的方法要优于其他几种方法。

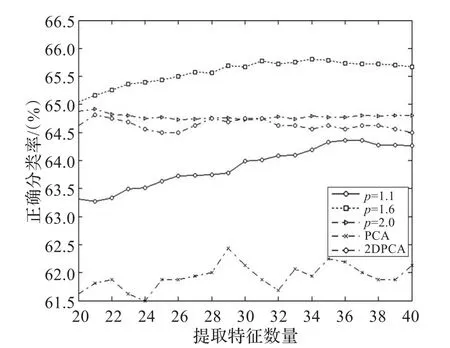
图2 在ORL上加入8×8的遮挡后性能的比较

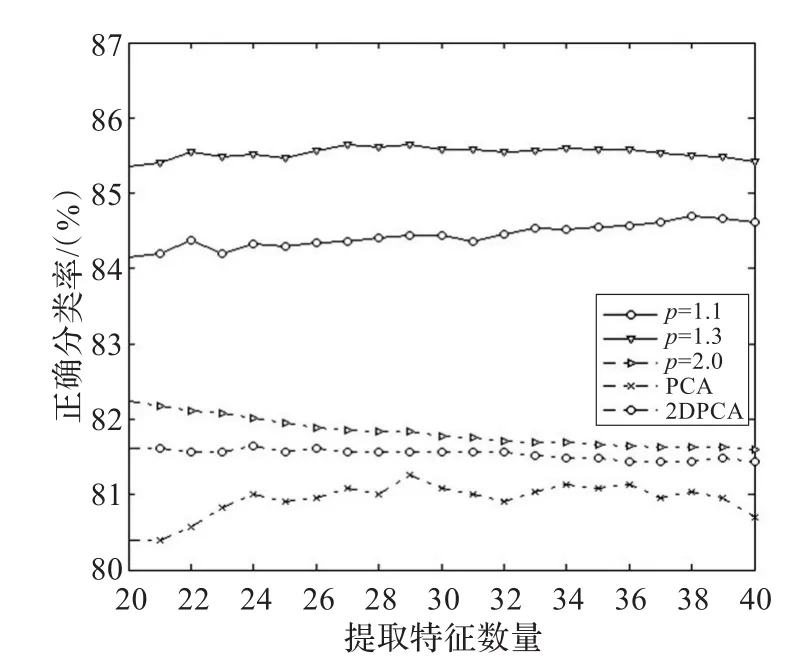
图3 在UMIST上性能的比较

从图2很明显地看出，当p=1.6时2DPCA-Lp方法取得最佳性能，并且比 PCA，2DPCA，2DPCA-L1（p=2.0）的性能好。

从表1可以看出，当取得最大正确分类率时，p=1.6～2.0等方法对应的提取特征数量较小，而p=1.1～1.5等方法对应的提取特征数量较大。这是因为当p较小时，得到的投影向量较稀有，因此需要更多的投影向量来进行识别以达到最大分类率。

遇到异常值的影响时，PCA，2DPCA，以及2DPCA-L1（p=2.0）的最高分类率都下降了，且2DPCA-Lp的下降率要大于其他方法。但是不管参数p怎样，2DPCA-Lp方法在性能上仍然高于其他的方法。本文方法的主要优点之一是当p取较小的值时，得到的投影可能是稀疏的。在求图像的特征时，最佳投影向量的稀疏使得图像中的异常值被滤去，进而使得异常值的影响降低。

4.2 UMIST数据库

在UMIST人脸数据库中继续测试提出算法的性能。在UMIST人脸库中，有20人，总共564幅图像。实验的方法与在ORL上的方法相同，部分实验结果如图3所示。

同样，在UMIST的图像上也加入8×8的块遮挡，测试这几种方法在有遮挡情况下的性能，部分实验结果如图4所示。各种方法的最佳识别率如表2所示。

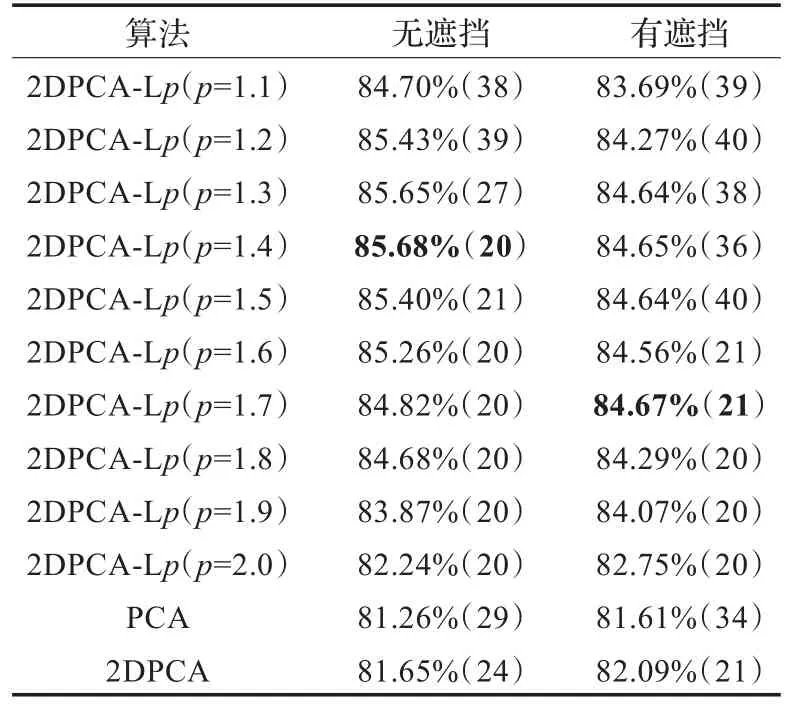
表2 UMIST上的最优分类率及对应的提取特征数量

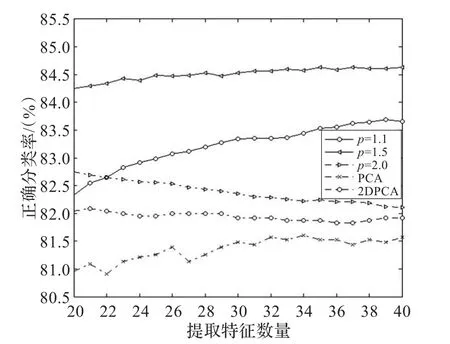
图4 在UMIST上加入8×8的遮挡后性能的比较

从图3可以看出，在分类性能上PCA算法最差，2DPCA算法优于PCA但又劣于2DPCA-L1，同时注意到2DPCA-Lp方法在p=1.3时性能最佳。

从图4同样可以发现2DPCA-Lp（p=1.5）比PCA，2DPCA，2DPCA-L1有更高的识别率和稳定性。从表2可以看出在无遮挡时，2DPCA-Lp（p=1.1至1.9）在最高分类率上，与PCA，2DPCA，2DPCA-L1的相比，之差分别为4.42%，4.03%，3.44%。有遮挡时，分别为3.06%，2.58%，1.92%。当无遮挡时p=1.4取得最优分类率，当有遮挡时p=1.7取得最优分类率。实验结果表明通过选择合适的参数p，本文方法优于其他方法。

5 结束语

本文首先介绍了PCA和2DPCA，然后提出了2DPCA-Lp。与2DPCA-L1相同的是，它在求最佳投影向量时的目标函数采用L1范数。不同的是它采用Lp范数进行约束，因此2DPCA-Lp是2DPCA-L1的一种推广，也可以说2DPCA-Lp是2DPCA-L1的一般化。它通过引入参数p对投影向量进行约束，这样可以选择合适的参数p，从而取得最好的分类性能。同时通过实验，表明2DPCA-Lp又比PCA，2DPCA，2DPCA-L1具有更高的识别率和鲁棒性。此外，如果文中算法在其他数据库中的性能不理想又如何进一步改进是今后的工作方向之一。

[1]Jolliffe I T.Principal component analysis[M].New York：Springer-Verlag，1986.

[2]Liu K，Cheng Y Q，Yang J Y，et al.Algebraic feature extraction for image recognition based on an optimal discriminant criterion[J].Pattern Recognition，1993，26（6）：903-911.

[3]杨键，杨静字.具有统计不相关性的图像投影鉴别分析及人脸识别[J].计算机研究与发展，2003，40（3）：447-452.

[4]Yang Jian，Zhang D，Yang Jing-yu.Two-dimensional PCA：a new approach to appearance-based face representation and recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26（1）：131-137.

[5]Baccini A，Besse P，Falguerolles A D.A L1-norm PCA and a heuristic approach[C]//Ordinal and Symbolic Data Analysis.Berlin：Springer，1996：359-368.

[6]KeQ，Kanade T.Robust subspace computation using L1 norm[R].Pittsburgh：Carnegie Mellon Univ，2003.

[7]Kwak N.Principal component analysis basedonL1-norm maximization[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2008，30（9）：1672-1680.

[8]Li Xuelong，Pang Yanwei，Yuan Yuan.L1-norm-based 2DPCA[J].IEEE Transactions on Systems，Man，and Cybernetics-Part B：Cybernetics，2009，40（4）：1170-1175.

[9]郭志强，杨杰.双向压缩二维特征抽取人脸识别新方法[J].计算机科学，2009，36（11）：296-299.

[10]夏道行，吴卓人，严绍宗，等.实变函数论与泛函分析[M].北京：高等教育出版社，2010.