影响图的渐进式构建方法
2013-04-03刘惟一
马 冯,刘惟一,杨 樱
MA Feng1,LIU Weiyi2,YANG Ying3
1.云南财经大学 信息学院,昆明 650221
2.云南大学 信息学院,昆明 650091
3.云南财经大学 国际工商学院,昆明 650221
1.School of Computer and Information,Yunnan University of Finance and Economics,Kunming 650221,China
2.School of Information Science and Engineering,Yunnan University,Kunming 650091,China
3.International Business School,Yunnan University of Finance and Economics,Kunming 650221,China
1 引言
影响图[1]作为一种有效的决策工具得到了人们广泛的关注,并在诸多领域[2-7]中应用广泛。然而,由于传统的影响图构建方法[8]需要专家或领域知识来确定原始数据集中变量间的相互关系,因此如果原始数据集增长,那么原有与之对应的影响图可能就不再适用于新的数据集了。此时,如果用传统的构建方法为新数据集构建影响图,那么就需要再次引入专家或领域知识来确认新环境下,各个变量间的关系如何,并重新构建一个适合新数据的影响图。
事实上,在大部分的实际应用中,新增长的数据集与原始数据集相比,大部分的变量变化程度很小。因此,本文针对这种情况,提出了一种影响图的渐进式构建方法,即在已知原始数据集和与之对应的影响图时,如果原始数据集增长,此方法可以通过调整现有影响图的结构和参数而获得一个适用于新数据集的新影响图。
这种方法的主要思想是,首先将与原始数据集对应的影响图转换为相应的简化图[9],然后对变化后的数据集,采用一个评分函数来判断当前的简化图是否适用于新数据。如果仍然适用,则仅需要调整各个变量的参数表即可。否则,需要先找出现有的简化图中差异度最大的地方。此处引入一个节点影响度的概念,用来判断各个节点对新数据的不符合程度。找出现有的简化图中影响度最大的节点,然后依据新数据对其进行调整,再利用评分函数对调整后的整个简化图进行评分。如果评分的结果已到达事先设定的阈值,则算法结束,否则,继续重复上述步骤,直至评分结果达到阈值为止。最后将获得的新简化图转换为影响图即可。
本文的主要贡献可以归结为以下两点:
(1)给定一个原始的数据集合对应的影响图,当原始数据集增长时,影响图的渐进式构建方法可以在不需要增加专家或领域知识的前提下,构建出一个新的符合要求的新影响图。
(2)影响图的渐进式构建方法在构建新的影响图时,只需要对原影响图进行局部调整即可,从而避免了从头开始重建一个影响图的问题。
2 背景知识
影响图是一种基于不确定性信息表示,用于处理复杂决策问题的图模型[1]。它包含两个部分:图结构和参数表。图结构表示数据集上变量间的依赖和时序关系,参数表体现了变量间的依赖程度。
定义2.1[1]影响图是一种有向无环图,它包含三种类型的节点:自然节点,决策节点和效用节点。变量间的相互影响关系,用节点间的箭头表示。
贝叶斯网,是一种可以用来表示变量间的相互影响关系的图模型。它也可以被看成是一种有向无环图,其中的节点表示随机变量,而有向边则表示变量间的相互关系。Pearl曾指出,贝叶斯网可以视为仅包含自然节点的影响图[10]。
定义2.2对于一个给定的影响图G,如果忽略节点的类型并将所有的节点都视为自然节点,那么它就变成了一个贝叶斯网,并且称这种图为影响图G的简化图。
然而贝叶斯网和影响图之间,还是有差异的,具体可以总结为以下几点[9]:
(1)影响图中的效用节点,不能有后继节点;贝叶斯网中无此限制。
(2)影响图中决策节点的顺序,必须要和现实世界中的实际情况一致。
(3)影响图中至少有一个决策节点和一个效用节点,并且决策节点应该是效用节点的祖先。
(4)影响图中的所有效用节点都要有对应的决策节点作为其祖先节点。
因此,在将影响图转化为其对应的简化图,即贝叶斯网时,或从贝叶斯网将其转换为影响图时,均需要遵循上述的几点规则。
3 影响图的渐进式构建方法
在影响图的渐进式构建方法中,有两个关键步骤:一个是构建影响图的图结构,另一个是计算图中各个变量的参数表。对于后一个步骤,刘惟一已经在文献[9]中给予了详细的描述,因此本文在此就不再冗述。本文提出的方法将专注于如何将原有影响图的结构调整成适合新数据的新结构。
3.1 影响图的渐进式构建方法描述
为了便于描述,假设Do是原始数据集,Dn是新数据集(原始数据增长以后的结果)。gido是原始数据集Do的影响图,go是 gido的简化图。 gidn是新数据集Dn的影响图,gn是 gidn的简化图。CH(go|Dn)是用来判断 go和 Dn之间的相符程度的评分函数,T表示事先设定的阈值。如果CH(go|Dn)的值小于T,则表示当前的go仍不适用于Dn。在描述具体的方法前,先给出一些相关和定义和定理,以便能够更加明确地说明方法执行的具体过程。
定义3.1.1如果xi是go的一个节点,那么xi的直接前驱节点就成为xi的父节点,记为Pa(xi)。
定理3.1.1如果xi是go的一个节点,是xi参数表中的值集,并且是Pa(xi)参数表中的值集,那么评分函数
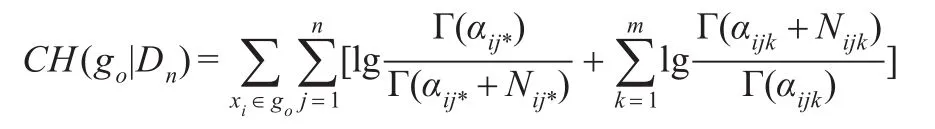
可以用来表示go和Dn之间的符合程度。
这个定理是Copper在文献[11]中给出的,并予以了证明。其中,Γ()是一个伽马函数,当n代表正整数时,Γ(n)=(n-1)!。Nijk代表Dn中符合并且条件的记录个数。αijk代表等价样本的个数。
定义3.1.2如果xi是go的一个节点,那么xi相对父节点的条件概率变化程度,Δ(p(xi|Pa(xi)))就称为节点xi对Dn的影响度。
定理3.1.2如果U是一个概率参数集,ukj∈U表示xi=并且时的条件概率,那么节点x对D的影响in度 Δ(p(xi|Pa(xi)))可以写成这里,“o”和“n”分别代表老的和新的训练数据集,并且r是U中概率参数的个数。
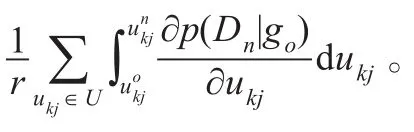
综上所述,影响图的渐进式构建方法(Incremental Building Method for Influence Diagram Structure,IBMIDS)的具体过程,可描述如下:
Input:
Do:原始数据集
Dn:新数据集
gido:原始数据的影响图
T:阈值
Output:
gidn:符合新数据集的影响图
Variables:
go:gido的简化图
gt:go的临时调整结果
gn:gidn的简化图
CH(gt|Dn):评分函数
xi:gt中的一个节点
步骤:
Begin
步骤1将gido转换为与其对应的简化图go
步骤2
(1)将当前的go记为临时调整结果gt。
(2)判断当前临时调整结果的评分制CH(gt|Dn)是否能够大于或等于阈值T。如果不满足条件,则循环执行下面几步直至满足条件为止。
①计算gt中每个节点xi的影响度,并找出影响度值最大的节点,记为xtag。
②在xtag的马尔科夫覆盖范围内,尝试着对边进行反向,增加或删除等操作对原图进行调整,从而将gt变为中间调整结果gt'。
③找出所有临时调整的图中,能够使得CH(gt'|Dn)取到最大值的那个,记为gt'。
④将临时调整结果gt调整成上一步找出的中间调整结果gt',并返回(2)的判断条件。
(3)将(2)中找出的最终 gt记录为新影响图的简化图gn。
步骤3将新影响图的简化图gn,按照第2部分中提到的方法转换成最终的新影响图gidn。
End
3.2 影响图的渐进式构建方法的有效性
定理3.2.1影响图的渐进式构建方法得出的最终结果gidn是符合新数据集Dn的。
证明 根据第2章中提到的影响图定义,如果gidn的结构能够表示Dn中变量间的依赖和时序关系,参数表体现了变量间的依赖程度,那么可以说gidn是符合Dn的。由于在结构上,gidn与gn是等价的,并且根据方法执行的过程可知,作为一个贝叶斯网,有CH(gn|Dn)≥T。因此,可以说明,gidn在结构上是符合Dn的。又由于在将gn转换为gidn的过程中,严格地遵守了第2章中提到的几条规则,因此可以确保各个变量在gidn中的时序关系与之在Dn中是一致的。获取各个变量参数表方法的有效性已经在文献[9]中被证明过了。因此,本文中提出的影响图的渐进式构建方法得出的最终结果gidn是符合新数据集Dn的。
4 实验和分析
4.1 实验
为了便于分析实验结果,实验选取了两个经典的数据集Hepar II[13]和Alarm[14]。现先以Hepar II为例,说明具体的实验过程。实验中,选取其原数据集中的部分变量进行实验,并将前100条记录作为Do,构建出的相应影响图为gido。
将Hepar II中的全部数据视为Dn,阈值T设定为0.95。首先,将 gido转换为 go,并得出CH(go|Dn)=0.83。由于CH(go|Dn)<T,因此下一步就是要找出影响度最大的节点。通过计算得知,是“Hepatic steatosis”这个节点。经过计算后得知,在“Hepatic steatosis”的各种调整方法中,删除“Hepatic steatosis”到“PBC”的边可以使得评分函数的值达到当前的最大值0.86。由于此时仍不满足事先设定的阈值要求,因此需要重复上述步骤,直至找到符合条件的图为止。最后,得到了一个合适的gn,使得CH(gn|Dn)=0.97。再将gn转换为gidn,如图1所示。
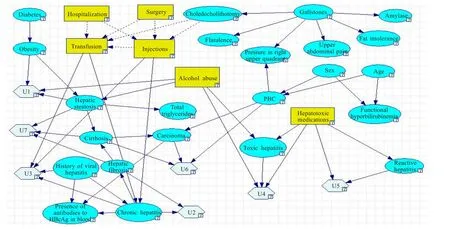
图1 IBMIDS构造出的Hepar II影响图
同理,可以用IBMIDS方法构建出Alarm数据集的影响图,如图2所示。
4.2 分析
文献[13]中已经给出了用传统方法基于Hepar II数据集构建的影响图,如图3所示。文献[14]中已经给出了用传统方法基于Alarm数据集构建的影响图,如图4所示。可以看出,图1与图3相比,图2与图4相比,两者均是等价的。因此,可以表明影响图的渐进式构建方法对于这两个经典的数据集都是有效的。
由于该方法的最终结果是由贝叶斯网转换而来的,但是对于一个给定的数据集,其有效的贝叶斯网结构并不唯一。因此,有时候影响图的渐进式构建方法得出的结果,并不一定与传统方法构建出的影响图在结构上完全一致,但这并不是说明该影响图是无效的。根据之前的讨论可知,它只是一个有效,但表现形式不同的影响图。
5 结束语
本文提出了一种影响图的渐进式构建方法。对于一个给定的数据集和与之对应的影响图,如果原数据集增长,那么该方法可以通过调整原影响图而得到一个适用于新数据集的新影响图。与传统方法相比,它可以有效减少影响图在构建过程中对专家或领域知识的依赖,避免了遇到新数据集时,需要重新构建影响图的情况。文中对该方法的有效性在理论上进行了证明,并用Hepar II数据集进行了实验验证。
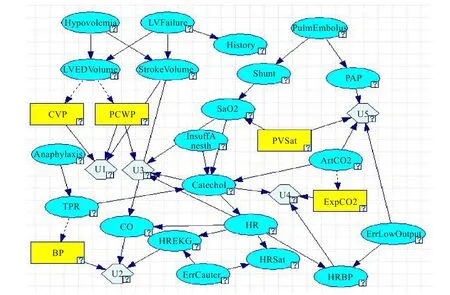
图2 IBMIDS构造出的Alarm影响图
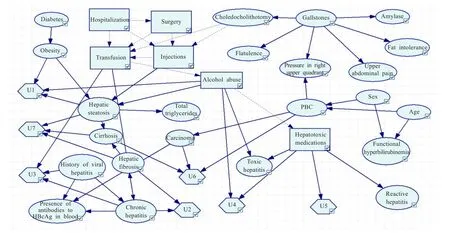
图3 用传统方法构建出的Hepar II影响图
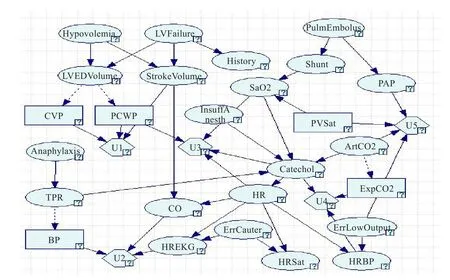
图4 用传统方法构建出的Alarm影响图
在经过大量的实验后发现,如果新数据集与原始数据集相比,大部分的变量在其分布情况上都发生了重大的变化,那么这种方法的效率就会受到很大的影响。因为此时每个节点都会耗费很多时间在与之相关的边调整上,以便于找到合适的新结构。如何改进这个问题,将会是下一步工作的重点。通过研究发现,现实应用中的大部分情况,其新数据集与原始数据集相比,都属于仅有小部分的变量在分布情况上有较大改变,其余大部分的变量变化很小的情况。因此,本文提出的方法在大部分的实际应用中都可以得到较好的结果。
[1]Howard R A,Matheson J E.Influence diagram[J].Decision Analysis,2005(3):127-143.
[2]Pauker S G,Wong J B.The influence of influence diagrams in medicine[J].Decision Analysis,2005,2:238-244.
[3]Meyer J,Phillips M H,Cho1 P S,et al.Application of influence diagrams to prostate intensity-modulated radiation therapy plan selection[J].Physics in Medicine and Biology,2004,49:1637-1653.
[4]Fernández del Pozo J A,Bielza C,Gómez M.A list-based compact representation for large decision tables management[J].European Journal of Operational Research,2005,160:638-662.
[5]Bielza C,Fernández del Pozo J A,Lucas P.Explaining clinical decisions by extracting regularity patterns[J].Decision Support Systems,2008,44:397-408.
[6]Shachter R D.Efficient value of information computation[C]//Proceedings of the 15th Annual Conference on Uncertainty in Artificial Intelligence(UAI-99).San Francisco,CA:Morgan Kaufmann,1999:594-602.
[7]Liao W H,Ji Q.Efficient non-myopic value-of-information computation for influence diagrams[J].International Journal of Approximate Reasoning,2008,49(2):436-450.
[8]Chung T Y,Kim J K,Kim S H.Building an influence diagram in a knowledge-based decision system[J].Expert Systems with Applications,1992,4(1):33-44.
[9]刘惟一,李维华,岳昆.智能数据分析[M].北京:科学出版社,2007:244-256.
[10]Pearl J.Probabilistic reasoning in intelligent systems:networks of plausible inference[M].California:Morgen Daufmann Publishers,1998:116-131.
[11]Cooper G,Herskovits E.A Bayesian method for the induction of probabilistic networks from data[J].Machine Learning,1992,9(4):309-347.
[12]Russel S,Norvig P.Artificial intelligence:a modern approach[M].Beijing:Posts&Telecom Press,2002:320-354.
[13]Li Oni_sko A,Druzdzel M J,Wasyluk H.Learning Bayesian network parameters from small data sets:application of Noisy-OR gates[J].International Journal of Approximate Reasoning,2001,27(2):165-182.
[14]Beinlich I A,Suermondt H J,Chavez R M,et al.The ALARM monitoring system:a case study with two probabilistic inference techniques for belief networks[C]//Proceedings of the 2nd European Conference on Artificial Intelligence in Medical Care,1989:247-256.
