基于UG和ANSYS Workbench的对辊辊形优化
2013-03-30程小明王晓红陈建魁
程小明,王晓红,陈建魁
(华中科技大学数字制造装备与技术国家重点实验室,湖北 武汉 430074)
0 引言
对辊常用于钢板冷轧[1]、薄膜复合[2]和薄膜输送[3]等场合。钢板冷轧使用金属钢辊,而薄膜复合、薄膜输送主要利用包裹橡胶层的钢辊或铝辊,称为橡胶金属辊。薄膜复合、薄膜输送都会使用2个橡胶金属辊,橡胶金属辊之间的压力分布对薄膜复合、薄膜输送均有较大影响。压力分布不均匀会使薄膜复合的压合效果不一致而影响成膜质量,也会使薄膜输送的张力增量不统一而导致薄膜褶皱[4]或跑偏[5],因此有必要研究橡胶金属辊之间的压力分布,并采取措施获得均匀的压力分布。
目前,国内求解橡胶金属辊间压力分布和辊形优化的文献较少,高鼎铭[6]通过数学推导得到轧制时的压力分布,白振华[7]用幂函数优化过轧辊辊形曲线,但对于小面积橡胶金属辊均不太适用;国外Parish[8]和 Ali[9]分别研究过橡胶金属辊和锥形辊间的压力分布,但通过压力分布曲线近似假设所获得的结果不够精确。将使用UG和ANSYS Workbench研究橡胶金属辊之间的压力分布,根据压力分布结果对2个橡胶金属辊(对辊)的辊形做进一步优化。
1 对辊压力分布
在优化对辊辊形之前须获得对辊压力分布规律,进行对辊压力分布仿真的步骤如图1所示。

图1 对辊压力分布求解步骤
1.1 压力分布仿真分析
图2为对辊接触宽度B、橡胶层厚度h和金属层直径d等3个几何参数直接影响对辊压力分布,其余几何参数根据支撑零件确定。利用这些参数在UG中建立三维模型,然后采用双向依附模式将UG模型导入ANSYS Workbench的DesignModeler模块中。

图2 对辊关键几何参数
关于对辊金属层,定义其密度ρ、弹性模量E和泊松比μ。橡胶层属于非线性材料,需额外指定屈服强度σy和切线模量ET。塑性变形发生与否需要通过后期的计算结果判断。
对辊接触在工作时既存在接触非线性,又存在材料非线性,是一种高度非线性行为[10],需要耗费较多资源。加之对辊接触是线或小面积接触,计算更加复杂,因而有必要仔细分析接触定义中的强制接触协调方法、接触类型、对称与非对称行为、接触探测区域和法向接触刚度等。
将上下辊子各组成一个“多体部件体”,每个多体部件体包含橡胶层和金属层2类实体。它们可分别设置材料属性,独立划分网格,之间的节点共享并无接触设置。此外,网格划分还需注意:①金属层变形小,橡胶层变形大,因此金属层的网格稀疏,分割后的接触橡胶层网格密集,其余网格稍稀疏,以减小计算规模;②网格尽量采用六面体二十节点单元,以进一步减小计算规模并保证计算精度;③网格应该关于2个法向接触中心面对称,以保证对称部分的节点位移和受力情况相同。
边界条件包含位移边界和载荷边界。上辊子受力压向下辊子,下辊子两端轴承支撑;然后下辊子被驱动着绕轴线旋转,上辊子受下辊子的摩擦力同步旋转。于是上辊子包含竖直、轴线旋转2个自由度,下辊子只含轴线旋转自由度。对于载荷条件,上辊子两端受向下压力,同时系统受重力。
对辊旋转速度很慢,可将仿真类型简化为静力学分析,研究对象是对辊接触线,研究内容包括接触线的节点位置、切向滑移、法向位移、压力、应力和应变等。组合这些数据可研究接触线处切向滑移和位置的关系、应力和应变的关系、压力和位置的关系、法向位移和位置的关系。从而既可判断橡胶层是否发生切向滑移、弹性变形,又可得到对辊之间的压力分布以及法向变形分布。
1.2 压力分布应用实例
在UG中建立对辊三维模型,对辊接触宽度B=250mm,橡胶层厚度h=5mm,金属层直径d=50mm。采用双向依附模式将三维模型导入ANSYS Workbench的DesignModeler模块中。接着分割对辊,上辊子橡胶层被分成5份:底部对称2份是接触探测区,左右对称2份是过渡区,顶部1份由平面附加产生。下辊子的分割方式类似。分割后确保只有2个多体部件体,每个多体部件体分别包含上下辊子的分割实体。
进入Engineering Data模块,按照表1中数据指定3种材料,并在后续材料定义中说明橡胶层为聚氨酯,上辊子金属层是钢,下辊子金属层是铝。

表1 3种材料属性
进入Model模块设置接触,选择分割后接触的四份橡胶层作为接触体,采用增广Lagrange法,摩擦接触类型,摩擦因数为0.4,对称接触行为,Pinball radius=6mm,程序控制法向接触刚度。接着采用MultiZone划分2个多体部件体网格,最后控制局部网格。
进入Setup模块添加7个边界条件。关于位移边界,分别设置下辊子的2个轴承端为圆柱体约束,切向自由;在上辊子的2个圆柱端分别建立局部坐标系,设置远程位移,轴向旋转和竖直位移自由。关于载荷边界,首先添加系统重力加速度,然后在上辊子两端的圆柱面上分别添加竖直向下的轴承载荷48N。最后进入Solution模块设置对辊接触线的节点位置、切向滑移、法向位移、压力、应力和应变等,直至计算结束。图3为对辊压力分布图,最大压力为0.106 75MPa,出现在接近橡胶层边缘,接触面积(条纹部分)非常小。组合上述数据,以揭示接触线的新规律。

图3 对辊接触压力分布
对于上下辊子接触线处节点切向滑移和节点位置的关系,节点切向滑移在1.98E-5~2.02E-5 mm之间,约等于0,因而接触线几乎无切向滑移,即对辊间无相对转动。对于下辊子接触线处节点应力和节点应变的变化规律,应力和应变呈现线性关系,由此判断在现有边界条件下,橡胶层之间仅发生弹性变形。图4为上下辊子接触线处节点压力和节点位置的关系曲线。由图4可知,①两曲线完全重合,上下辊子接触线处的压力分布一致,与实际相符;②最大压力0.107MPa,位置接近橡胶层边缘,说明此处变形最大;③最小压力0.078MPa,位置处于橡胶层边缘,主要由于橡胶层边缘无材料延续,压力突变,此处不适合作工作段;④-100~100mm区域的压力分布相对均匀,呈现“下凹”弧线分布,适合作为工作段。

图4 节点压力与节点位置的关系曲线
上下辊子接触线处节点法向位移和节点位置的关系曲线如图5所示。由图5可知,①上辊子接触线处节点法向位移处于0.050 8~0.052 3mm 之间,相隔0.001 7mm;下辊子接触线处节点法向位移处于0.067 5~0.069 1mm 之间,相隔0.001 6 mm,与上辊子接触线的变化范围几乎相等,说明二者接触紧密,与实际相符;②上辊子接触线处节点法向位移比下辊子接触线的小,说明上辊子轴线产生了“上凸”变形,下辊子产生了“下凹”变形,致使上辊子接触线在压力变形的基础上向上发生了刚体位移,下辊子向下发生了刚体位移;③接触线在橡胶层边缘存在变形突变,不适合作为工作段,与节点压力的规律类似;④-100~100mm区域的变形分布相对均匀,整体呈现“上凸”弧线分布,与”下凹”弧线压力分布反映的结果一致。因此,综合分析仿真数据,目前方案对辊接触处存在压力差异大、变形不均等问题。为得到更加均匀的压力分布,需要对对辊辊形进行优化。

图5 节点法向位移与节点位置的关系曲线
2 对辊辊形优化设计
对辊辊形优化设计包括几何建模、仿真建模、参数相关分析、响应曲面分析和驱动优化等过程。
2.1 几何建模
据已有分析结果,需将橡胶层外形设计成弧线形式。为使设计加工方便,暂将弧线定为二次曲线形式。ANSYS Workbench无法精确绘制二次曲线,UG则能实现,所以笔者将UG建模和ANSYS Workbench分析结合起来。图6为1/4辊形截面,不同于圆柱辊形之处是:橡胶层截面外轮廓由相切的直线段和二次曲线段组成,当直线段长度为0时,外轮廓就退化成一条二次曲线。以对辊轴线为X轴,对辊中心为原点O,竖直方向为Y轴建立直角坐标系。于是,橡胶层外轮廓方程为:
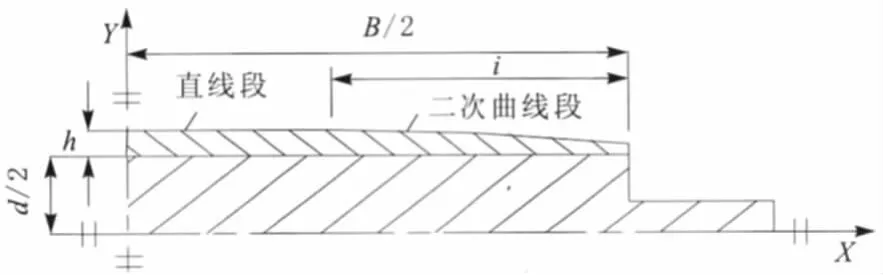
图6 1/4辊形截面

B为对辊接触宽度;h为橡胶层厚度;d为金属层直径;i为二次曲线顶点与边缘的偏距;a为二次项系数。在a的后面加上10-6是为了将a扩大106,避免在计算中出现“大数吃小数”以及在UG与ANSYS Workbench的数据传递中出现数据截断而带来较大误差。
在UG中建立h,d,i,a表达式,初始值定义为DS_h=5,DS_d=50,DS_i=80,DS_a=10.112 5。在每个变量的前面加上前缀DS,是便于ANSYS Workbench在模型生成过程中能识别。接着利用表达式绘制橡胶层轮廓曲线,通过实体操作得到对辊三维模型,每个橡胶层均是由弧线段、圆柱段和弧线段3部分组成。
2.2 优化仿真模型
建立有限元模型,然后划分网格,接触面增加了弧线段,其他接触设置未变。
定义边界条件和设置结果选项,计算得到橡胶层接触线的压力分布,最大压力0.032 5MPa与最小压力0.022 9MPa的比值为1.42。而对于圆柱对辊而言,最大压力0.107MPa与最小压力0.078 MPa的比值为1.37。可见对辊压力分布的均匀性并无改善,需要进一步优化设计。
2.3 参数相关性
参数相关性研究输入参数对结果的敏感性,下面将利用参数相关性研究橡胶层厚度DS_h,金属层直径DS_d,二次项系数DS_a,二次曲线偏距DS_i等4个设计参数对压力均匀性[7]Pmax/Pmin的影响。
首先将4个设计参数及Pmax/Pmin设为变量,接着进入 Design Exploration的 Parameters Correlation模块,指定3≤DS_h≤8,35≤DS_d≤55,0.1≤DS_a≤0.15,60≤DS_i≤100,然后创建50个设计点进行相关性计算,最后得到DS_h,DS_d,DS_a,DS_i与Pmax/Pmin的相关性和敏感性如表2所示。分析可知,①压力均匀性与4个参数的线性相关和二次相关均比较小,与二次曲线偏距的二次相关比线性相关要高,可见与4个参数是多次相关;②压力均匀性对橡胶层厚度、二次曲线偏距比较敏感,减小橡胶层厚度的上限或增大二次曲线偏距的下限均有利于减小压力均匀性;③压力均匀性对金属层直径不敏感,主要是金属层在所给范围内的刚性好,基本是橡胶层发生变形;④压力均匀性对二次项系数不敏感,需要增大DS_a的范围进一步观察。

表2 Pmax/Pmin与4个设计参数的相关性 mm
2.4 响应曲面
优化设计在ANSYS Workbench中是通过响应曲面(线)完成的。进入Design Exploration的Response Surface模块,按照表3设置参数。表中缩小了橡胶层厚度DS_h的上限,增大了金属层直径DS_d的下限、二次项系数DS_a的上限以及二次曲线偏距DS_i的上下限。

表3 Response Surface模块数据设置
随机计算80个实验数据点,根据kriging插值法得到响应曲面。压力均匀性对金属层直径、二次曲线偏距的响应曲面是一高阶函数曲面,耦合影响比较复杂。质量对橡胶层厚度、金属层直径的响应曲面是一平面,对橡胶层厚度的斜率小、对金属层直径的斜率大,表明质量受橡胶层厚度影响小,受金属层直径影响大,与实际相符。
2.5 目标驱动优化
目标驱动优化需在响应曲面的基础上指定目标。进入 Design Exploration的 Goal Driven Optimization模块后,将Pmax/Pmin,Gremetru Mass设置最小作为目标,Pmax/Pmin比 Gremetru Mass重要。采用筛选法从响应曲面上获取80个设计点进行计算。接着得到Pmax/Pmin,Gremetru Mass的重要程度权衡图,数值越大代表重要性越小,可以从中选取可行点作为候选优化点,也可选用系统推荐的候选优化点。
选取系统推荐的候选优化点为A(5.927 7,44.515 2,0.142 5,93.098 3)计算得到Pmax/Pmin=1.26,Gremetru Mass=4.94kg。图7为优化后的对辊压力分布曲线,最大压力为0.248MPa,最小压力为0.197MPa;橡胶层边缘的压力仍存在突变,不作为工作区间即可;-100~100mm的工作区域曲线接近一条水平直线,压力分布非常均匀,达到优化目的。最终优化出的对辊设计参数为:对辊接触宽度B=250mm,橡胶层厚度h=5.93mm,金属层直径d=44.52mm,二次曲线偏距i=93.1mm,二次项系数a=142 5。

图7 优化后节点压力与节点位置的关系曲线
3 结束语
利用UG和ANSYS Workbench分析出对辊之间的压力分布规律,通过结果说明对辊边缘压力存在突变,不适合作为工作区域;对辊中间压力呈现“下凹”弧线分布,需要优化。以压力均匀性、质量最小为目标确定出对应边界条件下的辊形参数,使对辊工作区域的压力分布更加均匀。目前市场上有部分厂家通过在金属辊外面包裹橡胶层的方式,改善薄膜输送对辊之间的压力分布,文中前期的压力分布结果体现出此方式产生的压力分布相对均匀。在此基础上按照特定的工况定量地进行辊形的优化设计,使得辊形结构更加合理。
研究没能确定外部载荷、辊形截面曲线与对辊压力分布函数的定量关系,尽管如此,通过文中的流程修改外部载荷,依然可以针对各种特定工况求出最优辊形参数。
[1]Mitsoulis E,Hatzikiriakos S G.Rolling of mozzarella cheese:Experiments and simulations[J].Journal of Food Engineering,2009,91(2):269-279.
[2]李智刚.柔性基板输送系统的结构优化及纠偏控制[D].武汉:华中科技大学,2008.
[3]Chevalier L,Eddhahak Ouni A,Cloupet S.On a simplified model for numerical simulation of wear during dry rolling contacts[J].Journal of Tribology,2009,131(1):1-15.
[4]杜星文,王长国,万志敏.空间薄膜结构的褶皱研究进展[J].力学进展,2006,36(2):187-199.
[5]Kang H,Lee C,Shin K.A novel cross directional register modeling and feedforward control in multi-layer roll-to-roll printing[J].Journal of Process Control,2010,20(5):643-652.
[6]高鼎铭.轧辊的压力分布[J].纺织机械,2002,(4):33-37.
[7]白振华,冯宪章,蒋岳峰.极薄带钢平整轧制过程辊型改造方案的研究[J].中国机械工程,2007,18(23):2887-2890.
[8]Parish G J.Calculation of the behaviour of rubber-covered pressure rollers[J].British Journal of Applied Physics,1961,12(7):333-336.
[9]Ali M,Shakoor M,Flugrad D,et al.Contact stresses in conical rollers[J].Journal of Strain Analysis for Engineering Design,2007,42(8):595-604.
[10]李 兵.ANSYS Workbench设计、仿真与优化[M].北京:清华大学出版社,2008.
