四足机器人在非规则地形上的路径规划

夏任司，孙容磊

（华中科技大学机械科学与工程学院数字制造装备与技术国家重点实验室，湖北 武汉 430074）

0 引言

与轮式机器人相比，足式机器人在地形适应性上有非常大的优势，但是非规则地形上的路径规划是其面临的重要难题。目前，大多数研究局限于保证机器人自身平衡和机器人基本步态的研究上，缺乏对足式机器人总体路径规划的研究，限制了足式机器人在野外探险、外星勘测和核电站救援等诸多复杂环境的应用[1]。

遗传算法作为一种启发式算法，具备搜索效率高，有自组织、自适应和自学习性，算法简便，易于实现的优点。近年来有关遗传算法的研究越来越活跃，进一步促进了遗传算法在各个领域的应用[2]。

四足机器人穿越非规则地形时，其四足按照运动需求以一定规律踩在地面。为保证机器人稳定行走，机器人在运动过程中不可以翻到并需要保证足够稳定裕度[3]，同时，机器人足底与踩踏地面不能存在相对滑动，因此非规则地形四足机器人路径规划是一个多因素影响下可行解求解问题[4]。提出了一种不规则地形下的智能路径生成算法：基于遗传算法的非规则地形上的四足机器人路径规划方法。综合考虑了机器人自身稳定性和机器人足与地面交互过程中的稳定性，得出问题可行域上的较优解，为非规则地形上的四足机器人的运动规划提出了一种有效方法。

1 环境表示和问题建模

对于非规则地形，优先采用静步态。静步态是各种步态中稳定性最佳的，它使得机器人始终有3条腿跟地面接触，而且它的慢速能为机器人赢取内部控制系统对自身状况、环境情况和自身与环境交互的分析控制时间，实现机器人的地形适应性。

对于移动机器人来说，获知环境信息是其进行各种活动的前提。为了获取地形信息，现在比较成熟的就是双摄像头和激光雷达组合的地形探测系统，通过地形探测系统来获取地形的完整信息。由于重点在于路径规划，所以设定地形信息为已知，即知道地形的高度起伏。将地形信息通过高程图表示，生成一个矩阵，矩阵每个元素的角标为位置，元素值为高度，这样就可以建立模型如图1所示。

图1 高程图

图中地形用矩阵A表示，机器人从S出发，目标为E点。这样就完成了问题的建模，即寻找一条路径，能让四足机器人从S点出发，顺利到达E点。同时，如果有关于机器人耗能和机器人运动距离的优化，也需要一并考虑进去。

2 机器人连续运动的离散化

四足机器人具体静步态运动过程如图2所示。

图2 静步态循环

从图2中可以看出，机器人在静步态运动的一个循环中，分出了6个步骤，先是一边的脚摆动，然后身体调整来保证后面阶段的运动，接着是另一边的脚摆动，然后继续身体调整，依次循环往复。在这个过程中，始终有不少于3只脚着地。

这样就可以把机器人的运动看成从前一个矩形过渡到后一个矩形，实现机器人连续运动的离散化。实际上，为了提高机器人的稳定性，一个运动循环中首尾四足着地状态，可以预设为平行四边形，如图3所示。

图3 静态模型

如此便将问题转化为在高程图上寻找一系列前后关联的着地点，这些点需要满足四足机器人运动的各种约束。

3 遗传算法的种群初始化

对于遗传算法，如何将问题解编码为种群个体，是算法使用过程中的关键问题。种群的设计直接影响到算法的工作效率和解的质量。经过多次试验，得出如下的种群设置方式能实现种群的良好收敛和较高的计算效率。

取机器人中心在地面的投影点为机器人每个离散状态的标记点，设定在标记点，机器人转身位姿为该标记点与上一步运动标记点的连线方向。通过投影点的坐标就可求出机器人四只脚的坐标。

种群的个体显然应该为若干个相互关联的标记点的集合，为了得到合理的路径，个体中的各个标记点应该首尾相接，同时从S点一次过度到E点。为此，把矩阵均匀划分为N块区域，如图4所示。

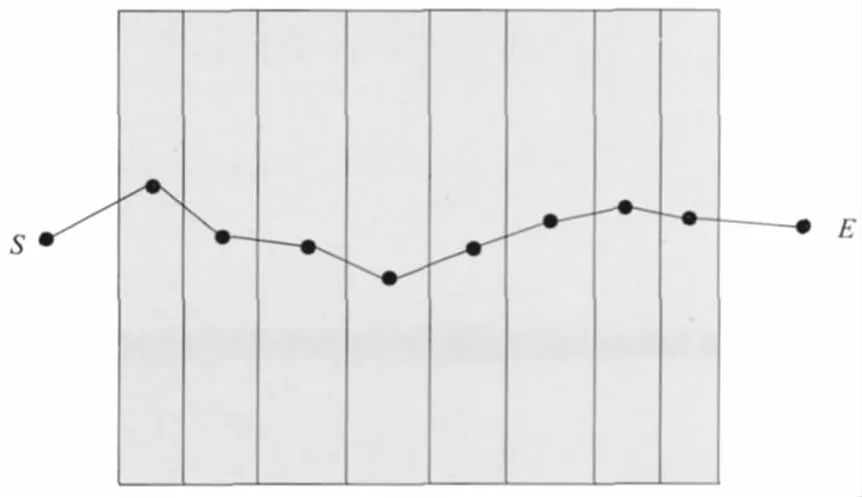
图4 问题建模

这样算法的个体就为从S点依次连接各个区域的点直到E点的点的集合。可以看出，所有个体的起点都是S点，终点都是E点，而且限制了机器人运动的步数为N＋1步。

算法的优化目标主要有2个。一是在路径序列点上机器人都能稳定；二是路径要足够顺滑，因为四足机器人的运动能力跟自身四足的尺寸，运动方式有很大的关系，例如对于K点和K＋1点，如果K＋1点与K点在纵向的距离过大，超出了机器人的运动能力，使得机器人根本无法在K点通过静步态运动到K＋1点，那么这样一条路径就是无效的。

通过算法实验发现，如果将这个约束放在适应度函数中考虑，种群的收敛性非常的差，几乎无法得到可用的规划路径。因此，在种群初始化中就将这一条考虑进去，即在初始化种群时，对于一个个体，除了S点，其余点的生成都与前一个点有关系，具体如图5所示。

图5 可选区域

4 适应性函数与进化方法

对于所涉及的问题，是很明显的多目标优化问题，选用分组进化方法。如图6所示。将种群分为2组，按照2个适应度来进行新种群的筛选，然后进行混合交配和随机变异即可。至于新种群的筛选，选用轮盘法，实现适应度值越大，存活概率越高的进化要求。

图6 混合进化

适应性函数的选择也是遗传算法的一个关键。对种群的选择主要考虑2个方面。一是机器人在路径序列点上要稳定；二是路径要足够顺滑。对于要求一，构建了四足机器人静态稳定模型。

模型的具体参数：

a.四只脚各自着地点地形的网格高度的偏差。

b.四只脚着地点之间的最大高度差。

c.机器人几何中心对应的地形高度与机器人身体的高度差。

对于要求二，关于路径顺滑性的要求，虽然在种群初始化中应经做了一定的考虑，但在进化过程中也需要考虑，做进一步的优化。

上式为考虑静步态稳定性的适应度计算公式。p1，p2，p3，p4为每只脚与地面接触的区域的网格高度的公差即地形平整度；H为着地点的最大高度差；cenh为机器人中心即序列点对应地形的高度。

采用exp指数函数是为了拉大各种地形情况的适应度值，同时为了进一步拉大各类地形的适应度值，提高进化效率，引入罚函数机制。

如果S＞y，S＝S＋100，否则S＝S。这样可以很好地淘汰完全站不稳的序列点。

对于第二点路径顺滑性，适应度函数直接用前后两点的纵向差的和的倒数。

这样对于所涉及的问题，算法能够实现较好的进化，得到合适的结果。

5 实验结果

在Matlab 6.0平台上进行该算法的仿真，图7为进化1 500代，耗时2 456s后搜索出的最优解。图中星点代表机器人的运动驻点，基本实现了路径规划的能力，让机器人顺利跨越可跨越障碍后，又避开了不可跨越高墙，使得算法基本实现了预定功能。

图7 仿真结果

6 结束语

所述遗传算法实现了一定的四足机器人路径规划的智能算法，较好的将四足机器人内部相互作用与机器人四足与地面的交互系统的统一在了一起，实现了四足机器人运动的全局规划。使得四足机器人摆脱了简单的循环规律运动，真正实现了高地形适应能力。但是目前该算法还存在耗时过长，效率过低，应用不灵活，对实时地理勘测系统依赖性过高等缺点。未来有望通过马尔可夫智能决策与遗传算法的结合来实现高效，高智能化的路径规划方法，真正发挥出四足机器人的强地形适应能力。

[1]孙明轩，黄宝健.迭代学习控制[M].北京：国防工业出版社，1999.

[2]Fang Z，Han Z G，Chen P N.Recent developments of iterative learning Control[J].Control Theory and Applications（S1672-6340），2002，19（2）：161-166.

[3]李俊仁，韩正之，唐厚君.一类迭代学习控制的自适应参数优化[J].系统仿真学报，2005，17（8）：1833-1836.

[4]吴 杰，许忠仁，詹习生，等.不确定性线性系统鲁棒迭代学习控制器设计及应用[J].自动化与仪表，2005，（5）：1-4.