负梯度浅海混响条件下吊放声纳主动探测深度研究

孙明太，周利辉，赵志允

（海军航空工程学院青岛校区，山东青岛266041）

当前反潜重点已由深海转入浅海海域，混响往往成为吊放声纳（以下简称吊声）主要干扰。在海上实验过程中发现，吊声在负梯度声速梯度条件下，通过调整探潜深度可产生混响聚集、回声信号纯净的现象。通过仿真和对吊声信号的分析发现，负梯度条件下，混响级随时延衰减的同时，在某些时段会出现“峰”现象，混响级明显高于相邻时段。

浅海混响以海底混响为主。海底混响的计算，主要包括声源到海底散射源的传播，海底散射源散射过程以及散射源到接收器的传播过程；吊声收发合置，声源与接收器处于同一位置。声纳与散射源之间的传播过程，目前主要以球面波体积扩展衰减和简正波方法进行研究[1-6]；海底散射源的散射包括不平整界面散射和海底沉积物体积散射，分别采用Lambert 模型及修正、GKirchhoff近似及扰动近似理论、体积散射理论进行分析。Jackson 等人提出了单基地高频海底散射模型[6]，分析了反向散射强度与掠射角、频率、海底声学参数的关系。

吊声工作频率较高，若采用球面波体积扩展衰减，计算简便，但假设条件过于理想；若采用简正波计算吊声与海底散射源之间的传播因素，高频情况下计算量较大。因此，本文采用高斯束射线Bellhop模型[7]计算混响传播衰减，采用Jackson 模型计算海底反向散射截面，进而计算混响衰减，结合信号余量的分析，对混响干扰下吊声工作深度的选择进行研究。

1 浅海混响计算

1.1 混响级

混响是由于海洋中大量无规则散射体及起伏不平的界面对入射声信号产生散射，在接收点上接收到的所有散射波的总和。混响的产生包括3 个过程：声源传播到散射源，散射源的散射过程以及散射声波传播到接收器。根据散射源不同可分为体积混响、海面混响、海底混响。在浅海中，混响强度的预报往往只需要考虑海底散射而忽略海面和体积散射。

本文采用Bellhop 模型计算声源传播到海底散射源和散射声压在接收器处的混响强度，海底散射源的散射过程采用Jackson模型。

时刻t的平均混响级为：

式（1）中：Q0为声源级；Hm、θmn分别为沿着路径m从吊声主动基阵到海底散射元dAmn的传播与掠射角；Hn、θ′mn分别为沿着路径n从海底散射元dAmn到吊声接收基阵的传播与掠射角；A(t)为脉宽时间τ0在时刻t对混响有贡献的所有海底散射面积；sb为海底散射元反向散射参数；B为吊声发射指向性图；B′为吊声接收指向性图。

1.2 海底反向散射参数

根据Jackson 模型，对于单基地声纳，设掠射角为θ，海底反向散射截面为sb(θ)=σbv+σbr。其中，σbr为不平整海底界面的散射截面，σbv为海底沉积物的体积散射截面。在小掠射角情况下，σbv为海底反向散射的主要贡献。吊声发射主动信号时，垂直波束宽度往往在±15°以内，满足小掠射角条件。因此，在计算吊声主动探测混响级时仅需对σbv进行计算[8-9]。

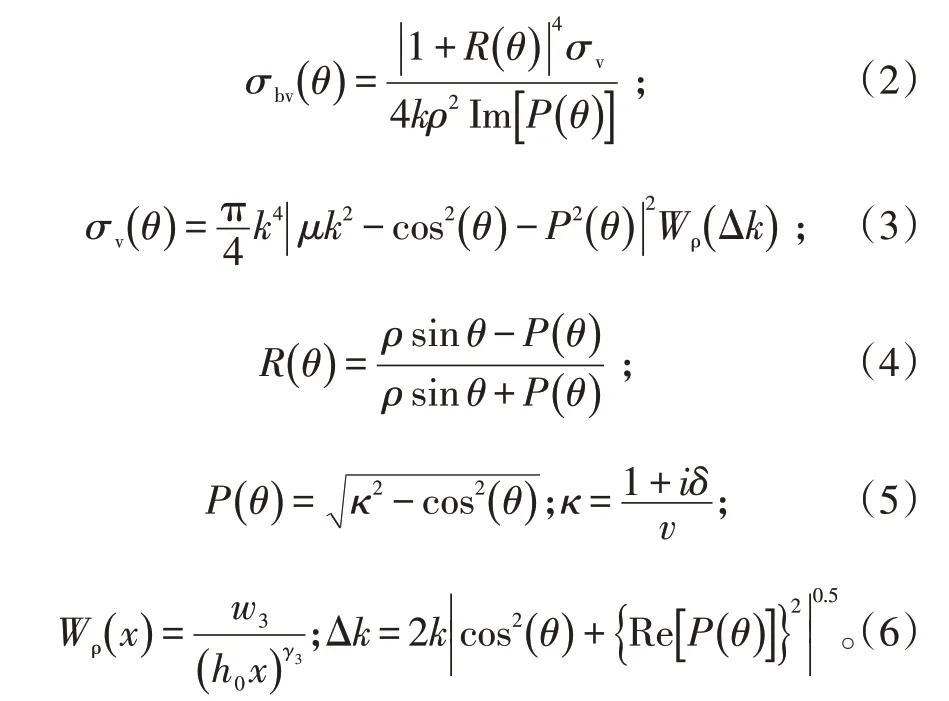
式（2）～（6）中：k为波数；ρ为海底沉积层与海水密度之比；v为海底沉积层与海水声速之比，δ为沉积物中虚波数和实波数的比率；w3为不均一性强度；γ3为不均一性指数；μ为沉积物中密度扰动的压缩比；h0为平衡量纲设定的参考长度（1 cm）。

1.3 混响传播因数

Porter 等人开发的Bellhop 模式采用高斯射线近似代替几何射线，能够较好地处理声线能量焦散和完全影区等问题。假设海底平坦，海深为z0，设吊声位置位于(zs,0)，散射元位于(z0,r)。根据Bellhop 模型，声能叠加采用半相干的计算方法，吊声位置(zs,0)到海底(z0,r)处的传播影响为：

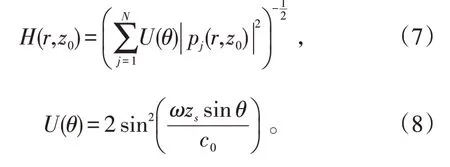
式（7）、（8）中：U(θ)为与掠射角θ有关的声线振幅的权重函数；N为由声源到达海底散射元dAmn的特征声线的个数；ω为圆频率；c0分别为声源处的声速；pj(r,z0)由Bellhop模型计算。

由声场的互易性，对于收发合置的吊声，Hm(θmn)=Hn(θ′mn)=H(θ)，仅需计算H(θ)。设吊声距海底高度为h，根据r=h/sinθ进行坐标转换，获取Bellhop模型计算结果，求得H(θ)。

1.4 海底散射面积与混响级计算

吊声发射主动信号时，垂直波束宽度往往在±15°以内，满足小掠射角条件。设脉宽为τ，对混响有贡献的海底散射面积A(t)近似为一个半径为r，宽度为0.5ct的海底圆环[10-11]。如图1所示，可以看出，dAmn≈rdφdr，θ=arcsin(h/r)=arcsin(2h/ct)。

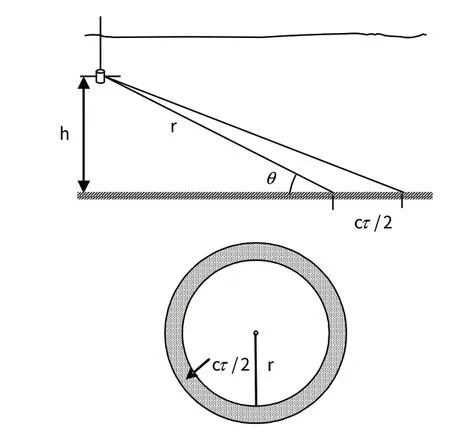
图1 海底散射面积计算

对于平坦海底，由于海底反向散射的各向同性，混响级计算起始时间为t0=2h/(csinθ)。混响为

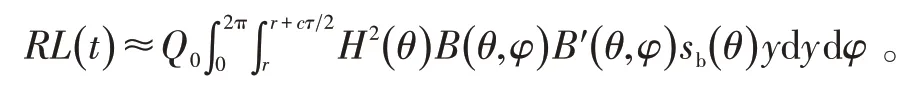
设B(θ,φ)=1，水平波束宽度Φ为12°，B′(θ,φ)为

则混响级化简为

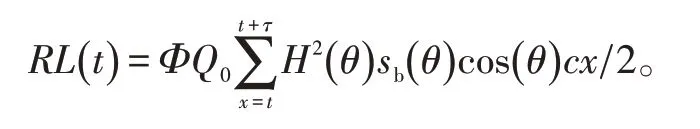
2 仿真与结果分析

2.1 海底混响计算与分析

设吊放声纳声源级为216 dB，发射频率9.0 kHz，发射脉宽39 ms，垂直波束宽度-15°～+15°。海水平均声速为c=1 500 m/s，t从t0到12 s以间隔0.001 s进行离散化。设反潜海域海深为70 m，泥沙底。为了分析梯度值对混响级的影响，取等声速与负梯度声场条件，声速梯度值分别为0 s-1、-0.085 7 s-1、-0.228 6 s-1、-0.371 4 s-1。吊声主动工作探潜深度在5～65 m 之间，间隔5 m取13个离散的值。图2～5为4个声速梯度值条件下，吊声不同探潜深度时，在12 s内，海底混响随时延衰减情况。

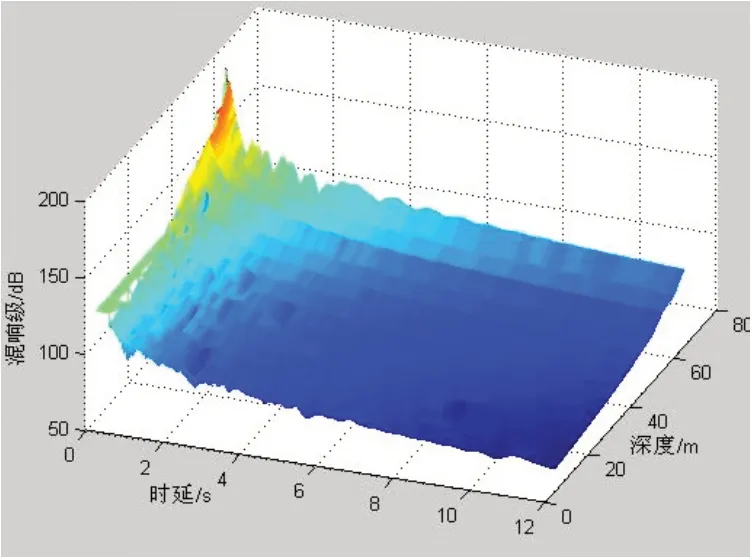
图2 等声速条件下海底混响级

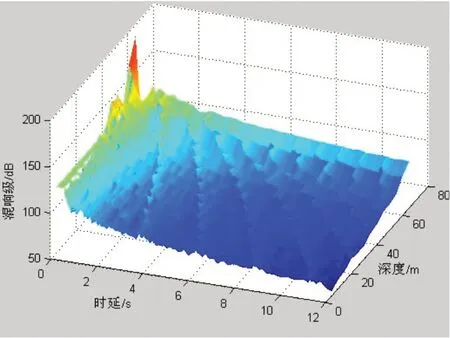
图3 声速梯度-0.085 7 s-1条件下海底混响级

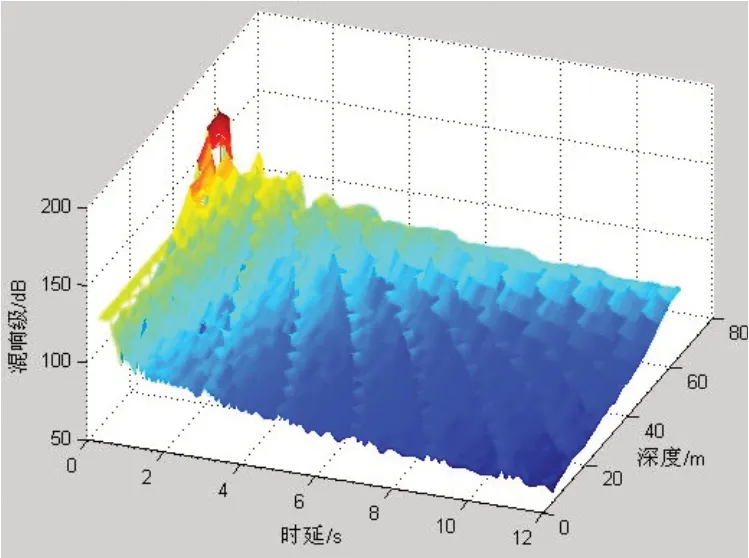
图4 声速梯度-0.228 6 s-1条件下海底混响级

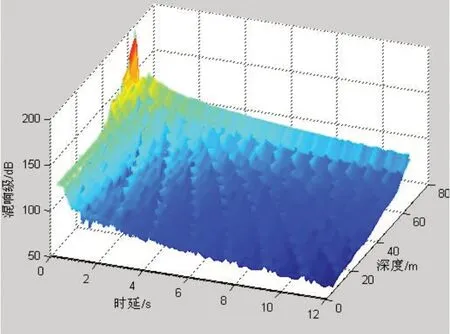
图5 声速梯度-0.371 4 s-1条件下海底混响级

从图2～5 可以看出，混响级总体上随吊声深度增大，随时延衰减。在负梯度条件下，在某些时刻出现混响“峰”现象，这是由于声线向海底弯曲造成的；在等声速条件下，仅在接近海底的深度出现较弱的混响“峰”现象。

混响峰数值分析结果见表1所示。从图3～5及表1可以看出，声速梯度和吊声深度相同前提下，混响峰高度随时延变小，峰之间间隔减小，但不明显；声速梯度相同，吊声深度不同时，混响峰高度随深度增大，峰之间间隔变小，即吊声深度减小时，混响峰呈现“展宽”现象；当声速梯度不同时，随着梯度值增大，混响峰高度增大，混响峰间隔减小，即随着声速梯度值减小时，混响峰呈现“展宽”现象；混响峰比相邻时间段混响级高15～20 dB左右，其中第1个“峰”时刻超出最多，其余依次递减；在接近海底的深度上，混响峰现象减弱，但整体上混响值较大。仿真与分析结果解释了吊声海上试验过程中通过调整探潜深度可以使得混响“聚集”的现象。

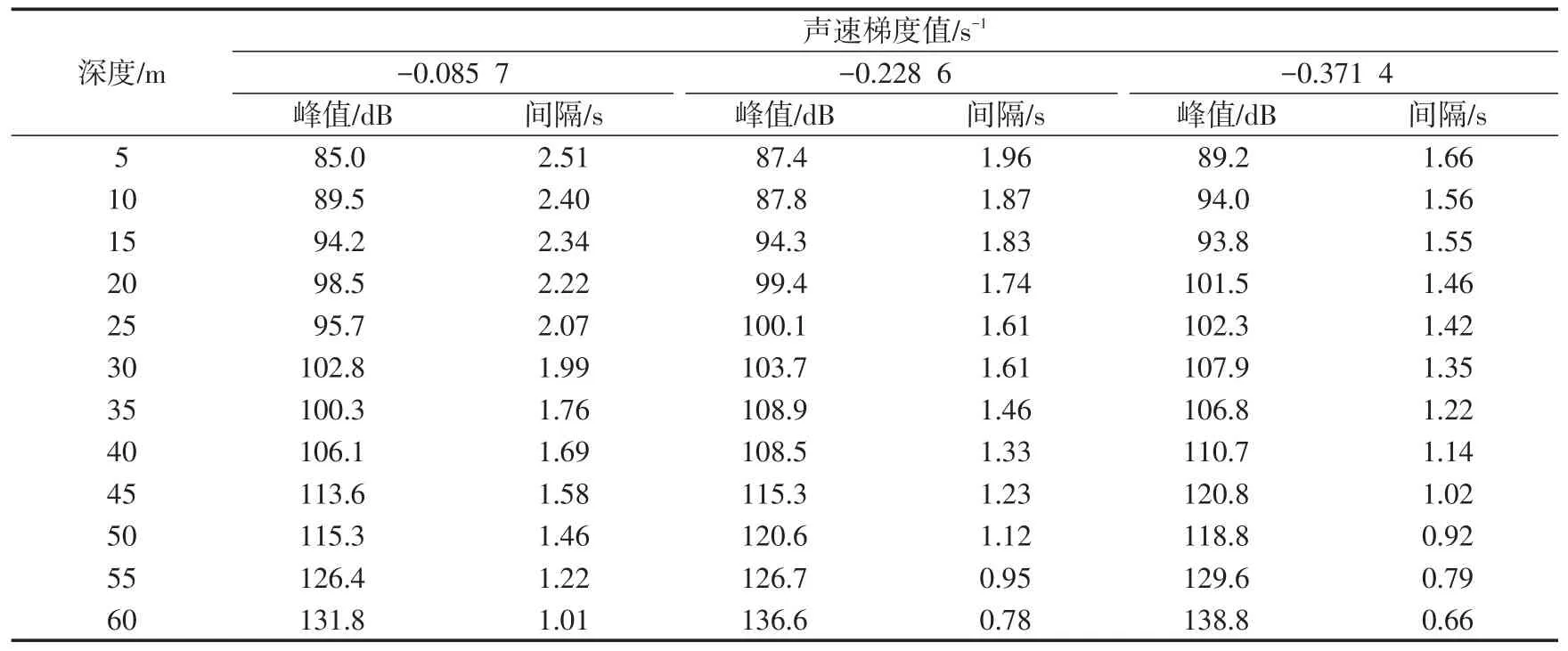
表1 混响首峰高度及峰间隔均值

2.2 吊声信号余量估算

设距离吊声足够小距离s0处的声压为q0(t)，则吊声发射声源声能级定义[12]为：

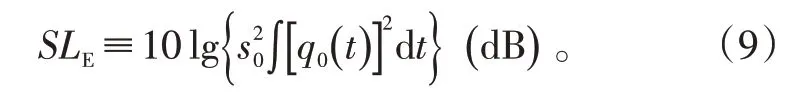
若在脉冲持续时间T内功率恒定，设均方声压（MSP）声源级为SL，则，

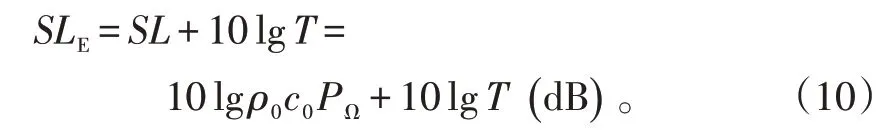
式（9）、（10）中：ρ0c0为吊声处海水特性阻抗；PΩ为单位立体角声功率。

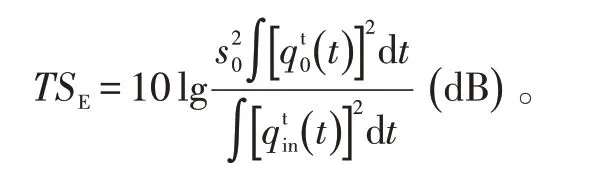
设声能传播损失因子为F，则，

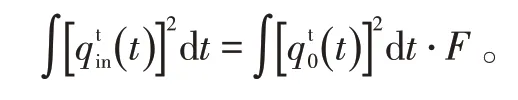
声能传播损失定义为

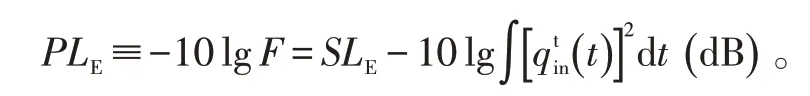
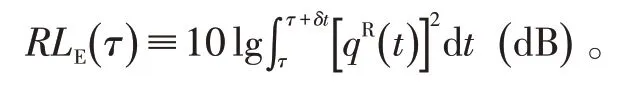
设声纳传感器处的信混比Rhp，波束形成后的信混比为Rarr，则声纳列增益为

设吊声信混比门限，即检测概率为p时的信混比为Rp，则检测阈为

信号余量定义为：

根据声纳方程各项的估算，即可计算吊声阵列输出信号余量SEE。

2.3 负梯度浅海条件下吊声主动探测深度选择

不失一般性，取梯度值为-0.228 6 s-1的负梯度声速条件，吊声探测深度为10 m、25 m，潜艇目标弦角60°，潜艇处于不同深度时的信号余量计算结果如图6所示。可以看出，吊声在10 m、25 m探测时，大多数混响峰处于不同时延处。计算结果显示，混响峰出现时，信号余量低于0，吊声很难发现潜艇目标；混响峰出现与否，信号余量相差最大可达10 dB以上；在同一距离上，当潜艇深度不同时，信号余量通常在小于3～5 dB。

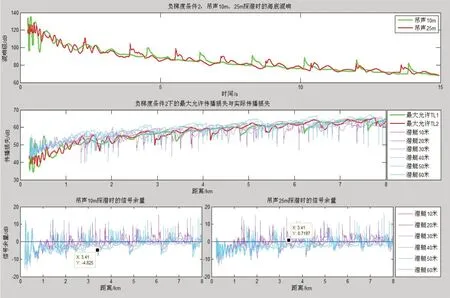
图6 声速梯度-0.228 6 s-1条件吊声10 m、25 m探潜时信号余量分析

经分析可知，负梯度条件下混响为主要干扰背景时，由于混响峰现象的存在，不应单独考虑同深探测的问题。通过对从图3～5及表1的分析，总体上看，吊声应尽量在靠近海面的深度进行探测，此时混响级整体水平较低，且混响峰高度最小，峰之间间隔也较大；同时吊声应适当增大深度补充探测一次，以免回声信号掩蔽在混响峰区域。例如，在图5所示的情况下，吊声在10 m 探潜时，在4.56 s 处出现混响峰，当潜艇目标距离吊声3.41 km，且深度在10～60 m 之间时，信号余量为-8～-4 dB之间，吊声很难发现潜艇。此时，若吊声改变探测深度，在25 m 探测，可使目标回波信号偏离混响峰时刻，此时信号余量为-1～2 dB之间，吊声发现概率明显提高。

3 结论

仿真与分析结果表明，负梯度条件下，浅海混响整体随时间衰减，在某些时刻出现“峰”现象，混响级高于相邻时间段10～15 dB。其出现时刻（即位置）、间隔、高度随时延变小；随着吊声工作深度减小，混响峰数量、高度减小，间隔增大，呈现展宽现象；随着梯度值减小，混响峰高度减小，混响峰间隔增大，也呈现展宽现象，混响峰现象减弱；在接近海底的深度上，混响峰现象减弱，整体上混响值较大。

负梯度浅海条件下，吊声主动探测时，吊声应首先在接近海面深度探测，使混响能量集中在较小的时间间隔内；然后，适当增大工作深度进行补充探测，避免潜艇目标回声信号掩蔽在混响峰区域，以提高搜潜效果。

[1] 杨丽，蔡志明.混响背景下单双基地声纳的探测范围比较[J].系统仿真学报，2006，18（11）：3263-3266.

YANG LI，CAI ZHIMING. Comparison of detectable region for bistatic and monostatic sonar in reverberation background[J]. Journal of System Simulation，2006，18（11）：3263-3266.（in Chinese）

[2] 吴金荣，孙辉，黄益旺.浅海近程混响衰减[J].哈尔滨工程大学学报，2002，23（6）：4-8.

WU JINRONG，SUN HUI，HUANG YIWANG. Short range reverberation intensity decaying in shallow water[J]. Journal of Harbin Engineering University，2002，23（6）：4-8.（in Chinese）

[3] 高伟.浅海混响统计反演海底声参数和界面统计参数研究[D].青岛：中国海洋大学，2008.

GAO WEI. Statistical inversion of acoustical and statistical parameters of seafloor from shallow water reverberation[D]. Qingdao：Ocean University of China，2008.（in Chinese）

[4] 笪良龙.海洋水声环境效应建模与应用[M].北京：科学出版社，2012：43-49.

DA LIANGLONG. Ocean acoustical environment effectiveness modeling and application[M]. Beijing：Science Press，2012：43-49.（in Chinese）

[5] 张明辉.三维环境海洋混响强度衰减规律研究[D].哈尔滨：哈尔滨工程大学，2005.

ZHANG MINGHUI. Research on decaying law of oceanic reverberation intensity in three dimensions[D].Harbin：Harbin Engineering University，2005.（in Chinese）

[6] MOURAD D D，JACKSON DR. High frequency sonar equation medels for bottom backscatter and forward loss[C]//Proceedings of OCEANS.1989：1168-1175.

[7] PORTER M B. Bellhop Manual and User’s Guide[EB/OL]. USA：Heat，Light and Sound Research Inc.，（2011-01-31）[2012-04-17]. http：//oalib.hlsresearch.com/Rays/HLS-2010-1.pdf.

[8] HOLLAND C W，NEUMANN P. Sub-bottom scattering：a modeling approach[J]. Journal of the Acoustical Society of America，1998，104：1363-1370.

[9] 徐超.海底散射模型与多波束混响信号统计特性研究[D].哈尔滨：哈尔滨工程大学，2009.

XU CHAO.Research of seafloor scattering model and statistical characteristic of multibeam reverberation signal[D]. Harbin：Harbin Engineering University，2009.（in Chinese）

[10]郭熙业，苏绍璟，王跃科，等.收发合置情况下海底混响仿真[J].国防科技大学学报，2010，32（2）：141-145.

GUO XIYE，SU SHAOJING，WANG YUEKE，et al. Research on simulating seafloor reverberation in the case of monostatic[J]. Journal of National University of Defense Techology，2010，32（2）：141-145.（in Chinese）

[11]赵烨，冯西安，郑玉峰，等.海底混响的空时模型及仿真[J].计算机仿真，2011，28（12）：398-401.

ZHAO YE，FENG XIAN，ZHENG YUFENG，et al.Simulation and space-time model of seafloor reverberation[J].Computer Simulation，2011，28（12）：398-401.（in Chinese）

[12] MICHAEL A AINSLIE. Principles of sonar performance modelling[M]. Berlin：Springer & Chichester：Praxis，2010：53-122.