最优1→3对称型经济实态量子克隆的固态电路实现方案

赵英燕，王 辉，陈 娟，姜年权

（温州大学物理与电子信息工程学院，浙江温州 325035）

最优1→3对称型经济实态量子克隆的固态电路实现方案

赵英燕，王 辉，陈 娟，姜年权†

（温州大学物理与电子信息工程学院，浙江温州 325035）

提出一种最优1→3对称型经济实态量子克隆的固态电路实现方案.在方案中，通过利用磁脉冲控制磁通量、电荷和穿过约瑟夫森结的相位差来实现最优1→3对称型经济实态量子克隆.经济实态量子克隆只需要对比特进行操作，不需要其它辅助操作，实验上简化了量子克隆的实现过程.由于超导比特具有耦合强度强，又没有非线性电感和能量的耗散等优点.相比于腔QED系统，固态系统在实验上便于集成和操作.

经济实态量子克隆；固态电路；超导比特

近些年，量子信息科学得到了广泛的关注[1-2]，主要是因为它提出了一些新的处理量子通信和量子计算的方法.在量子信息科学中，最显著地特点是对于任意的量子态不可能被精确地复制.Buzek[3]和Vion[4]是最早提出能够获得未知量子态两个拷贝的近似量子克隆的科学家.若二维空间量子克隆的输入态为=+1，且相位φ∈[0,2π），其中α，β为振幅，满足正交归一化条件=1.根据输入态的信息不同，可将量子克隆分为以下三类：当α，β和φ完全未知时，称普适量子克隆（universal quantum cloning machine，UQCM）；当α和β已知，φ未知时，称相位量子克隆（phase-covariant quantum cloning，PCC）；当φ已知，α和β未知时，称实态量子克隆（real state cloning，RSC），对于最优实态量子克隆是指态矢作用到初始态幺正变换后，保真度可达到FSERS=56.经济型的量子克隆只需要对量子比特进行操作，不需要其它的辅助性操作，因此，在实验上极大的简化了量子克隆的实现过程.相比于其它的量子克隆，经济型量子克隆在实验上提高了效率.

目前，作为量子计算机的信息存储和处理单元——量子比特，已经在许多物理系统被广泛研究，如离子阱、腔QED、核磁共振和量子点等.根据约瑟夫森结耦合能和单电子库伦阻塞能的相对大小，已实现的超导约瑟夫森量子比特可分为电荷量子比特、磁通量子比特和相位量子比特三种类型.近年来，Wendin和Shumeiko等人[5-6]对超导量子比特、超导量子电路和计算做了系统的研究和总结.在量子计算中，引起计算误差的主要原因是量子比特的消相干.在固态系统中，超导量子比特是关键因素，量子比特不可避免的要同外部环境耦合，从而导致量子计算出错.因此，如何克服超导量子比特的消相干是实现量子计算机的关键.超导系统作为量子计算机的最佳候选人之一，已成为科学研究的热点.相比于离子阱、腔QED、波色爱因斯坦凝聚等系统，超导系统更便于操纵和扩展.在过去几年，量子克隆的实现已在腔QED[7-14]系统得到了证明.本文将通过控制磁通量、电荷和穿过约瑟夫森结的相位差来实现最优的1→3对称型经济实态量子克隆.

1 最优1→3对称型经济实态量子克隆的实现

我们选用一个由超导量子干涉器件（superconducting quantum interference devices，SQUID）组成的量子电路，SQUID可作为一个耦合器，通过SQUID每一个电荷比特都可以和其它的电荷比特进行选择性耦合.图1 – 3描述的是基本的电荷比特及比特间的耦合电路图.

图1 第i个电荷比特模型图（右侧）,等效电路图（左侧）

图2 Couper对（右侧）,等效电路图（左侧）

图3 三个电荷比特耦合原理图

系统的哈密顿量为：

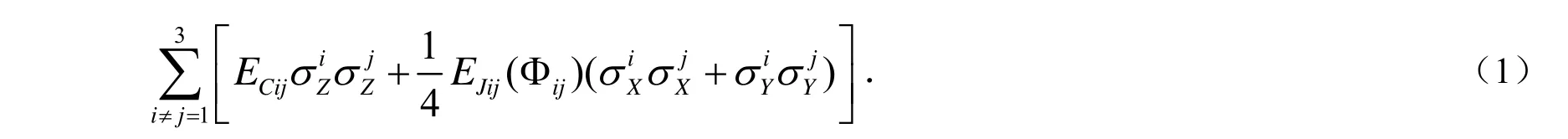
在ECij非常小时，我们可以忽略第三项，目前这个条件在实验上很容易做到.当我们选取系统的哈密顿量简化为：

系统相互作用的哈密顿量为：

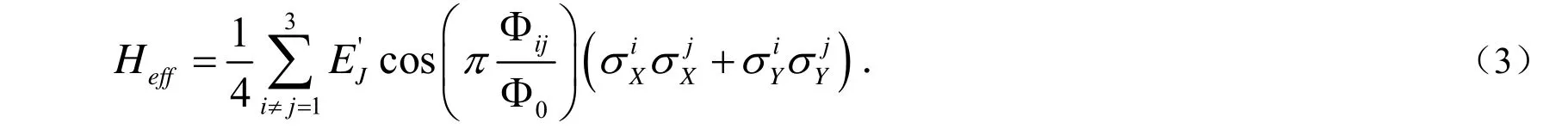
当Φij=0时，两比特间相互作用耦合强度最强，

则相互作用的哈密顿量为

在基矢空间中，两个比特的基矢表示为{|00＞,|01＞,|10＞,|11＞}，相应的演化算符矩阵：

下面我们将证明如何实现3比特的对称型经济实态量子克隆（symmetric economical real state cloning，SERSC）.

假设比特1的输入态为|ψ＞1=α|0＞1+eiφβ|1＞1，其中α和β满足归一化条件，即|α|2+|β|2=1,φ∈[0,2π）.其它两个比特最初制备的态为|10＞，通过调节磁场和门电压使比23特2和3发生耦合，相互作用时间t后，系统的输出态为：

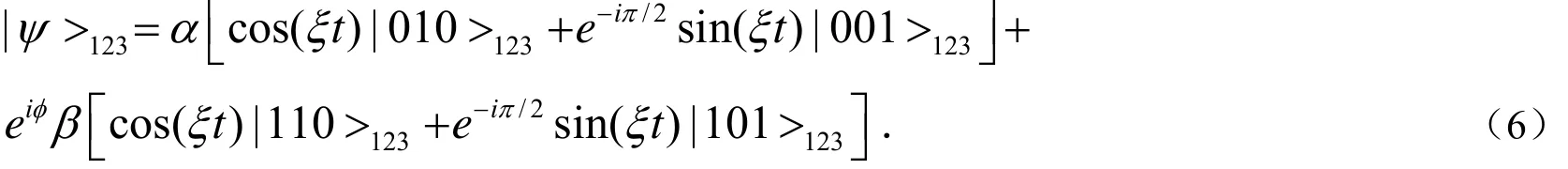
具体操作过程如下：

（1）当ng1=ng2=，ΦX1=ΦX2=ΦX3时，我们把（2）式中的耦合项比作开关，选取外加磁通量Φij=2nΦ0，于是=0，开关关闭.

（2）当Φ=0，比特2和3发生耦合，系统的有效哈密顿量为

23

让比特2沿着Z方向旋转角θ1，满足条件（m取整数），n=1，g 3相应哈密顿量表示为则系统的态矢可以用如下形式描述：

（3）比特1，2和比特1，3同时执行C-NOT门操作[15]，通过调节外加磁通量和们电压，我们可以很容易得到第i个比特和第j个比特的C-NOT门，即

执行上面的变换后，（7）式变成

（4）对比特2进行单比特操作，即|0＞2→|1＞2,|1＞2→|0＞2，则（9）式将表示为：

（5）对比特1沿着Z方向旋转，转角为θ，即|0＞→e-iθ2|0＞，|1＞→eiθ2|1＞，整个21111系统演化态矢描述为：

图4为实现SERSC原理图，其中Ri（i=1,2）是单比特操作，U23（ξt）表示比特2和比特3的变换，符号⊕表示对于每一个比特的NOT操作，即|1＞→|0＞和|0＞→|1＞.X表示比特沿着X方向旋转.

图4 SERSC原理图

假设输入态矢为|ψ＞1=α|0＞1+β|1＞1，系统参数满足条件φ=，θ2=0，cos（ξt）=，sin（ξt）=，（11）式表示为：

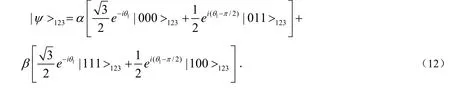
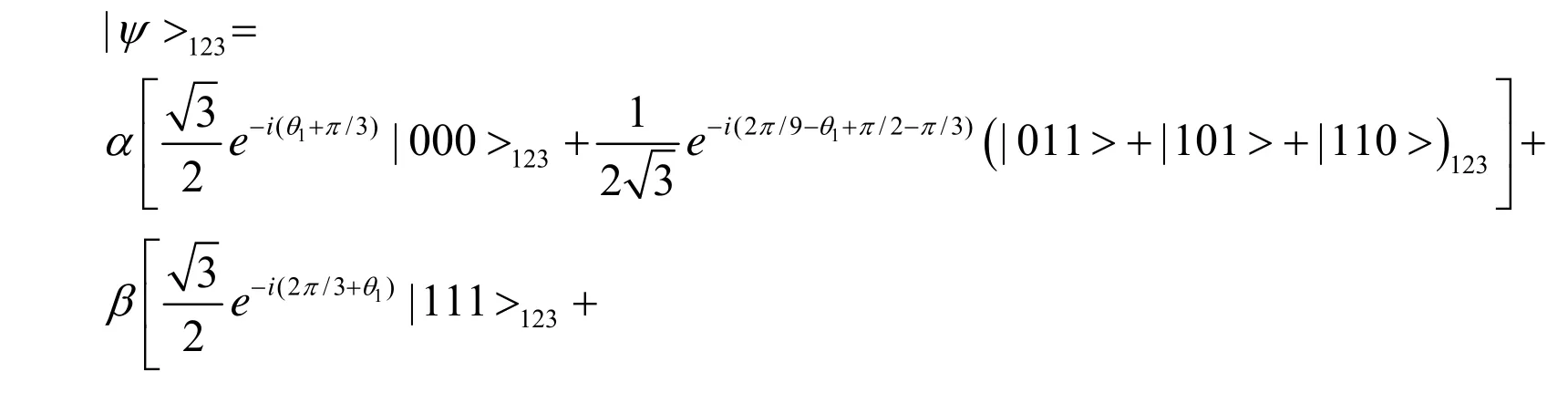
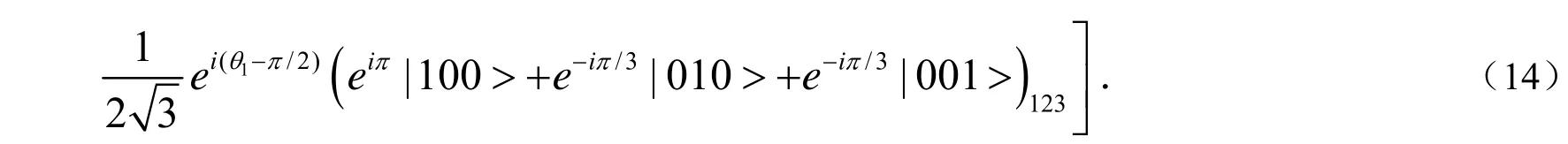
当选取Φ23=0，比特2和比特3发生耦合，相互作用时间t后，态矢表示为：

比特3沿Z方向进行单比特操作，转角为θ3，相应哈密顿量为则整个系统的态矢为：

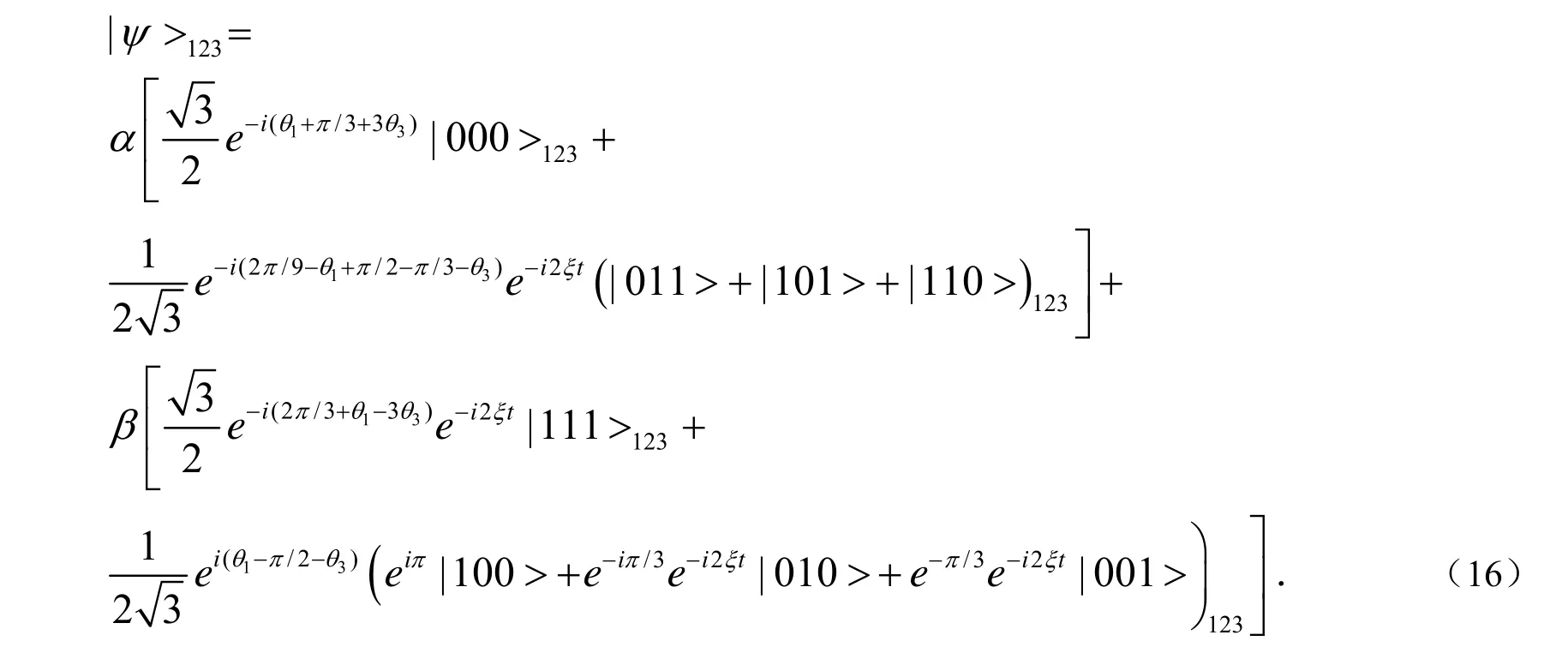
为了实现最优1→3对称型经济实态量子克隆，我们选取恰当的参数θ=-，θ=-，13Ωt=-，即

其中，常相位ei19π/36可以被忽略.当保真度时，称对称型的相位协变量子克隆.

2 结论与讨论

在实验上，C-NOT门[17]和SWAP门[18]的操作时间top远小于能量的弛豫时间tr，Tc=Q2πμ是固态电路的可操作时间，其中Q和μ分别是固态电路的质量指标和谐振腔频率，操作过程中相应的概率为P≅toptr，根据理论计算，固态电路中的有效衰退时间Tc/P ＞＞tr，此方案在实验上是可行的.

本文给出了实现最优1→3对称型经济实态量子克隆的模型及理论推导.在操作实验电路的过程中，运用不同逻辑门间的操作，制备所需的量子态，这种门操作的形式可以简单、清楚表示量子态的制备过程，便于该量子态传输过程中数据分析.本文的研究价值在于，对于经济型实态量子克隆只需要对比特进行操作，不需要其它辅助操作，实验上简化了量子克隆的实现过程.由于超导比特具有耦合强度强，又没有非线性电感和能量的耗散等优点.相比于腔QED系统，固态系统在实验上便于集成和操作.

[1] Wang Y H, Song H S.Preparation of multi-atom specially entangled W-class state and splitting quantum information [J].China Science Bull, 2009, 54：2599-2605.

[2] Zhang Y J, Xia Y J, Man Z X, et al.Simulation of the Ising model, memory for Bell states and generation of four-atom entangled states in cavity QED [J].Science in China Series G：Physics Mechanics ＆ Astronomy, 2009, 52：700-707.

[3] Bužek V, Hillery M, Werner R F.Optimal manipulations with qubits：Universal-NOT gate [J].Physical Review A, 1999, 60：R2626-R2629.

[4] Vion D, Aassime A, Cottet A, et al.Manipulating the quantum state of an electrical circuit [J].Science, 2002, 296：886-889.

[5] Wendin G, Shumeiko V S.Quantum bits with Josephson junctions [J].Low Temperature Physics, 2007, 33：724-725.

[6] Lofwander T, Shumeiko V S, Wendin G.Andreev bound states in high-Tc superconducting juntions [J].Superconductor Science and Technology, 2001, 14：53-58.

[7] Song Q M, Fang B L, Wu T, et al.Optical realization of optimal symmetric universal and phase-covariant quantum cloning [J].Journal of Modern Optics, 2011, 58：160-164.

[8] Zheng S B, Guo G C.Entangling and cloning machine with increasing robustness against decoherence as the number of qubits increases [J].Physical Review A, 2005, 72：064303-064307.

[9] Zhang W H, Ye L.Scheme to implement general economical phase-covariant telecloning [J].Physical Letter A, 2006, 353：130-137.

[10] Zhao Z, Zhang A N, Zhou X Q, et al.Experimental Realization of Optimal Asymmetric Cloning and Telecloning via Partial Teleportation [J].Physical Review Letter, 2005, 95：030502-030506.

[11] Chen H W, Lu D W, Chong B, et al.Experimental Demonstration of Probabilistic Quantum Cloning [J].Physical Review Letter, 2011, 106：180404-180408.

[12] Sabuncu M, Andersen U L, Leuchs G.Experimental Demonstration of Continuous Variable Cloning withPhase-Conjugate Inputs [J].Physical Review Letter, 2007, 98：170503-170520.

[13] Sabuncu M, Leuchs G, Anderson U L.Experimental continuous-variable cloning of partial quantum information [J].Physical Review A, 2008, 78：052312-052317.

[14] Hu J Z, Yu Z W, Wang X B.Quantum cloning machine of a state in a belt of Bloch sphere [J].European Physical Journal D, 2009, 51：381-385.

[15] Astafev O, Pashkin Y A, Nakamura Y, et al.Quantum Noise in the Josephson Charge Qubit [J].Physical Letter A, 2004, 93：267007-267011.

[16] Dagmar B, Mirko C, D’Ariano G M, Chiara M.Phase-covariant quantum cloning [J].Physical Review A, 2000, 62：12302-12309.

[17] McDermott R, Simmonds R W, Steffen M, et al.Simultaneous State Measurement of Coupled Josephson Phase Qubits [J].Science, 2005, 307：1299-1302.

[18] Wu D H, Yang M, Cao Z L.Generation of remote W-type entangled state via tripartite entanglement swapping of continuous variables [J].Optics communications, 2009, 282：1944-1947.

A Scheme to Implement the Optimal 1→3 Economical Real State Quantum Cloning in Solid State Circuit

ZHAO Yingyan, WANG Hui, CHEN Juan, JIANG Nianquan
（School of Physics and Electronic Information Engineering, Wenzhou, China 325035）

We design a solid-state circuit scheme to implement the optimal 1→3 symmetric economical real state cloning in solid state circuit.In this scheme, our quantum cloning is obtained by using electromagnetic pulses to control the magnetic flux, the charge and the phase difference across a Josephson junction （a device with nonlinear inductance and no energy dissipation）.The economical cloning machine, which will greatly simplify the experimental implementation, does not require any ancilla except SQUID qubits.Compared to the cavity QED system, due to much stronger coupling constant in this circuit, the solid system is easy for integration and operation.

Economical Real State Quantum Cloning；Solid State Circuit；Superconducting Qubit

O413.2

A

1674-3563（2013）04-0024-08

10.3875/j.issn.1674-3563.2013.04.005 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：封毅）

2013-03-02

国家自然科学基金（10947017/A05）

赵英燕（1987- ），女，黑龙江鹤岗人，硕士研究生，研究方向：量子信息