广义指数分布场合下简单步进应力加速寿命试验的最优设计

李新翼，郑海鹰

（温州大学数学与信息科学学院，浙江温州 325035）

广义指数分布场合下简单步进应力加速寿命试验的最优设计

李新翼，郑海鹰†

（温州大学数学与信息科学学院，浙江温州 325035）

对加速寿命试验进行最优设计，不仅可以使产品的各种可靠性指标获得更准确的估计，而且也能够节省试验的时间和费用.针对简单步进应力加速寿命试验，以在正常应力水平下给定时间可靠性估计的渐进方差最小为标准，提出了定时截尾场合下，广义指数分布函数步进应力加速寿命试验的优化设计模型，并通过理论推导，得到了相应的优化设计方案.

加速寿命试验；广义指数分布；渐近方差；最优设计

由于制造设计的持续改进，高寿命、高可靠性的电子产品越来越多，应用也越来越广泛，对于这些高可靠性的产品或材料的寿命，想通过在正常条件下的测试来获得有关产品的寿命信息是非常困难的.例如[1]，不少电子器件的寿命很长，在正常工作温度40℃下可达数百万小时以上，若取1 000个这样的电子器件，进行数万小时的试验，可能也只有一两个失效，甚至没有一个失效，这些对产品的可靠性评估是非常不利的.假如我们把工作温度由40℃提高到60℃，甚至80℃，只要失效机理不变，由于工作环境变得恶劣，电子器件的失效个数会增多，这对评估高温下的可靠性指标是很有利的，这种在超过正常应力水平下的寿命试验称为加速寿命试验.

加速寿命试验方法主要有三种：一是恒定应力加速寿命试验，简称恒加试验；二是步进应力加速寿命试验，简称步加试验；三是序进应力加速寿命试验，简称序加试验.陈文华[2]从试验时间和试验样本量上对三种加速寿命试验进行了比较，发现步进加速寿命试验具有试验样本失效快、所需样本量小、试验设备简单等优点，因此，步进加速寿命试验的应用更为广泛.

有关加速试验的最优化问题最早是由H.Chernoff于1962年提出的.R.Miller和W.B.Nelso[3]应用极大似然法讨论了步加试验的最优设计，茆诗松[4]应用线性估计方法讨论了简单步加试验的优化设计.所谓最优化问题就是在加速寿命试验中，确定各个应力水平下的试验样本数和每个应力水平下的截尾时间，从而使正常应力水平下某种特定参数的估计量的方差达到最小.通常情况下，我们以对数平均寿命的极大似然估计（MLE）渐进方差或者对数分位点的MLE的渐进方差达到最小为标准.本文将在定时截尾场合下，建立寿命分布服从广义指数分布的简单步进应力加速寿命模型，并以在正常的应力水平下，在给定时间ζ，可靠性估计的渐进方差最小为标准来讨论试验方案的优化设计问题.

1 简单步进应力加速寿命试验

1.1 加速试验方案

假设初期n 个独立同分布的电子器件在应力水平为S1下进行加速寿命试验，当试验进行到时间τ时，把应力水平增加到S2，试验继续，直到全部部件都失效或者达到预先设定的结尾时间T.n1表示从试验开始到τ时失效的器件数，n2表示从时间τ到结尾时间T失效的部件数.根据试验方案，在加速寿命试验中能够观察到电子器件的失效时刻，从而可以得到一组观测值：1.2 加速试验方案的模型假设

假设1 在简单步加应力加速寿命试验中，两个加速应力记为S1和S2（S1＜S2），S0是正常情况下的应力水平.

假设2 在任何应力水平下，产品的寿命都服从广义指数分布，其分布函数为：

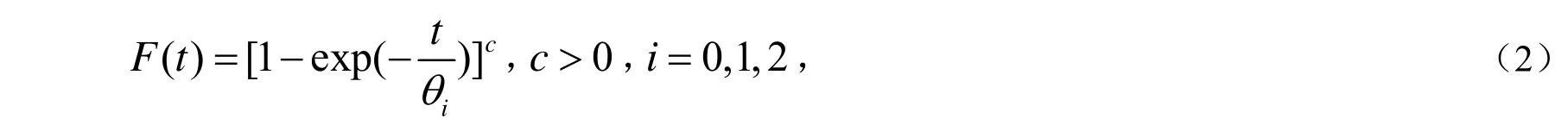
其中c 是形状参数，θi是尺度参数.

假设3 尺度参数θi与应力水平Si有如下对数线性关系：

这里的0β和1β是未知参数，取决于试验样品的性质和测试方法.

假设4 累计失效模型：产品的剩余寿命仅依赖于当时已累积的失效部分及当时的应力水平,而与累积的方式无关.

假设4可以认为是：在应力水平Si下，产品工作ti时间内累积失效的概率Fi（ti），相当于此种产品在应力水平Sj下工作tij时间内累积失效的概率，即Fi（ti）=Fj（tij），其中i≠j，从概率角度看，在应力水平Si下产品工作时间ti相当于在应力水平Sj下工作时间tij.

根据累计失效模型，简单步进加速试验下产品的累积分布函数为：

根据式（2）、（4）、（5）可得：

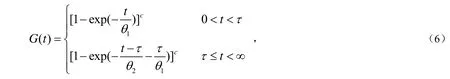
进而可得概率密度函数为：

2 用于加速寿命试验的极大似然理论

2.1 参数的极大似然估计

在加速寿命试验参数估计分析中，极大似然估计法是最重要和应用最广泛的参数估计方法.由（1）式可以得到似然函数：

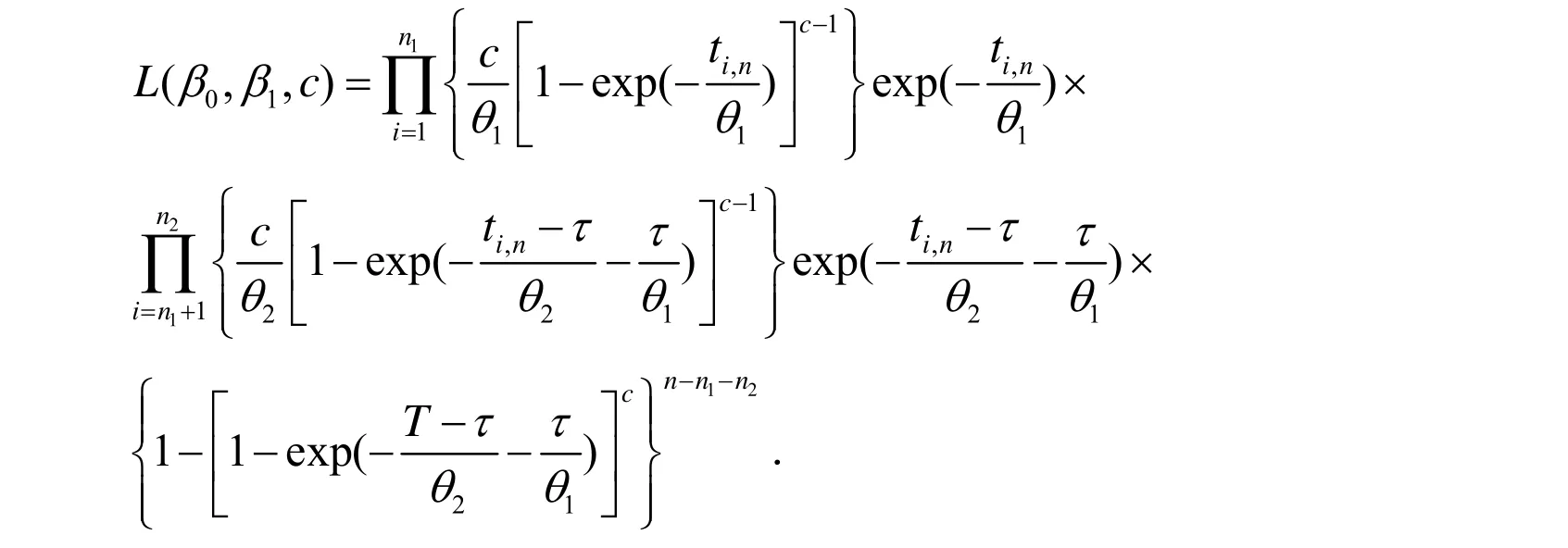
通常情况下，比较容易得到的是自然对数似然函数的最大化，而不是似然函数本身，因此，对数似然函数为：

对数似然函数分别对β0、β1和c求一阶偏导数，并令一阶偏导数等于零：

其中，

2.2 Fisher信息矩阵

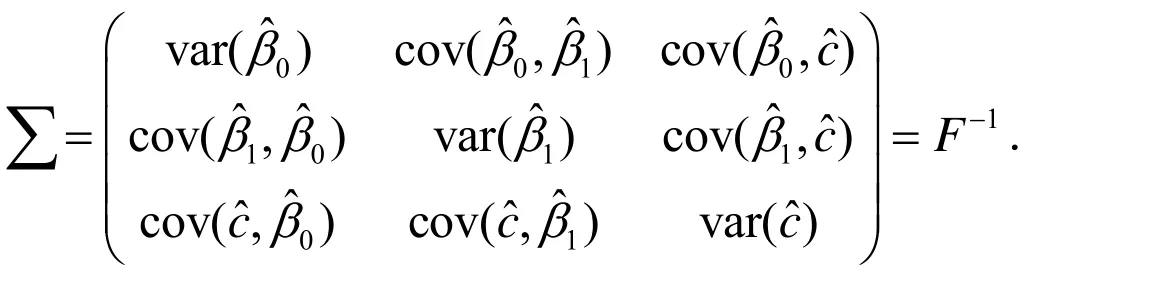
由于信息矩阵为似然函数负二阶偏导数矩阵的数学期望，想得到确切的上述期望的数学表达式是非常困难的，根据文献[5]，信息矩阵元素似然函数负二阶偏导数矩阵的数学期望可用负二阶偏导数的值来近似，即：

3 简单步进应力加速寿命试验的优化设计

在简单步进加速寿命试验中，通过对试验方案的优化找到最优的试验应力水平和应力变化点，可以达到节约试验成本、提高统计精度的目的.最优设计标准一般是以设定应力下对数平均寿命的MLE的渐近方差最小为标准，或以设定应力下对数分位点的MLE的渐近方差最小为标准，例如，文献[6]以设定应力下平均寿命的极大似然估计的渐近方差最小作为优化标准.但是，对于广义指数分布，在设定应力下平均寿命是很难得到的，考虑到可靠性函数和故障平均时间的关系，即MTTF=R（t）dt ，本文以在正常应力水平下，在给定时间ζ，可靠性估计的渐进方差最小为优化标准，因此，最优设计的关键是要求在正常的应力水平下，在给定时间ζ，可靠性估计的渐进方差达到最小.

在正常的应力水平下，在给定时间ζ，可靠性估计的极大似然估计是：

在正常的应力水平下，在给定时间ζ，可靠性估计的渐进方差为：

式中H为：

试验方案的最优设计方法就是：对于给定的时间ζ、n、截尾时间T、应力水平S1和S2以及、和ˆ的值，求出正常应力水平S0和应力变化点τ的值，使得AV（）达到最小.

4 结 语

本文主要讨论了简单步进应力加速寿命试验方案优化设计的准则和方法，并建立了在定时截尾场合下简单步进应力加速寿命试验方案优化设计的数学模型，最后给出了试验方案的最优设计方法.

[1] 茆诗松, 王玲玲.加速寿命试验[M].北京：科学出版社, 1997：3.

[2] 陈文华, 刘俊俊, 潘骏, 等.步进应力加速试验方案优化设计理论与方法[J].机器工程学报, 2010, 46（10）：182-187.

[3] Miller R, Nelson W B.Optmum simple step-strees plans for accelerated life testing [J].IEEE Trans on Reliability, 1983, R32（1）：59.

[4] 茆诗松.简单步进应力加速寿命试验及最优设计[J].应用概率统计, 1989, 15（2）：173-179.

[5] Cohen A C.Maximum likelihood estimation in the weibull distribution based on complete and on censored samples [J].Technometrics, 1965, 7（4）：579-588.

[6] 施方, 葛广平.Weibull分布场合下简单步进应力加速寿命试验的最优设计[J].上海大学学报：自然科学版, 1998, 4（3）：248-249.

The Optimal Design for the Accelerated Life Tests of Simple Step-stress under Generalized Exponential Distributions

LI Xinyi, ZHENG Haiying
（School of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035）

The optimal design of accelerated life test can not only make a variety of product reliability indexes obtain a more accurate estimate, but also can save the time and cost of the test.In view of simple step-stress tests for accelerated life, optimization criterion being defined as minimizing the AV of the reliability estimate at a specified time under normal operating condition, optimal design model is proposed of generalized exponential distribution function under step stress accelerated life tests based on Type I censoring.Through the theoretical derivations, the corresponding optimal design plan is obtained.

Accelerated Life Tests；Generalized Exponential Distributions；Asymptotic Variance；Optimal Design

O213

A

1674-3563（2013）04-0012-06

10.3875/j.issn.1674-3563.2013.04.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2012-12-27

李新翼（1987- ），男，安徽合肥人，硕士研究生，研究方向：应用统计.† 通讯作者，wzzhying@163.com