应用软件复杂条件处理的详细设计方法 —— N+2表法

王 咏

（温州大学物理与电子信息工程学院，浙江温州 325035）

应用软件复杂条件处理的详细设计方法
—— N+2表法

王 咏

（温州大学物理与电子信息工程学院，浙江温州 325035）

对于应用软件中复杂条件处理或加工的详细设计，针对传统的过程设计工具存在的问题，依据集合论提出了N+2表方法.该方法通过构造特定结构的二维表——N+2表来快速获取处理逻辑，用行扫描算法替代嵌套的多层条件判断以实现处理逻辑，更为重要的是该方法使得条件组合、动作以及二者之间的映射独立于程序和算法，通过元组增、删、改操作就可以实现处理逻辑的动态变化.多个信息系统的开发实践表明，该方法比传统方法具有明显的优势.

复杂条件处理；详细设计方法；N+2表

详细设计阶段是软件生命周期中的一个重要阶段.详细设计的根本目标是确定应该怎样具体地实现所要求的系统，也就是应该得出对目标系统的精确描述从而在编码阶段可以把这个描述直接翻译成用某种程序设计语言书写的程序[1].因此，在详细设计阶段，人们会根据需要选择图形、表格和语言等过程设计工具来简明清晰地表示程序处理过程，即处理算法.

应用软件的分析设计中经常会涉及复杂条件的处理或加工问题，比如保险、贷款等信息系统，需要根据给出的多个条件的不同组合及其处理规则设计出处理算法.传统方法是采用判定表[2]或判定树作为过程设计工具，即首先构造一张判定表（如表1所示），然后将其归并去除冗余优化为判定树，最后将判定树转变为嵌套的多层多条件判断（IF-THEN-ELSE）从而得到处理算法.随着条件数量的增多和每种条件取值的增多，这种传统方法将存在以下3个问题：

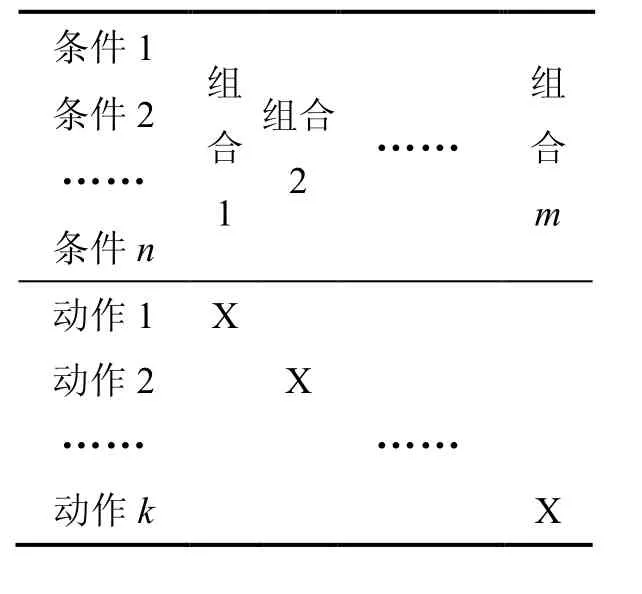
表1 传统判定表

1）快速获取处理逻辑困难

条件越多，每种条件的取值越多，条件的组合就会越多，判定表也就会越复杂，判定表向判定树的转换也随之会变得更加复杂，因此快速获取处理逻辑很难做到，同时也会使获取处理逻辑这一过程更加依赖于分析设计人员的经验.

2）业务逻辑动态改变无法实现

处理逻辑或处理规则是否能够实现动态改变是很多应用软件用户关注的问题之一.对于复杂条件的处理或加工，这就要求条件组合和处理动作之间的对应关系能够动态改变.但是采用传统的判定表等方法，条件组合和处理动作的对应关系都是通过编程在代码级定义的，因而，一旦软件开发完成，这种对应关系就无法改变，除非每次业务逻辑改变都去修改源代码，否则无法实现业务逻辑的动态变化要求.

3）程序可读性和维护性差

传统做法中将判定表转换为判定树之后，详细设计人员采用嵌套的多层多条件判断（IFTHEN-ELSE）来实现处理逻辑.随着条件的增多和每种条件的取值的增多，条件判断的嵌套层次数和条件数量都会随之增加，这就使得程序算法变得更加繁冗复杂，程序可读性和维护性随之大幅下降.

近十年来国内外涉及判定表的研究大都与问题1）相关.在这些工作中判定表是一个重要的获取加工逻辑的工具，学者们在规则生成算法、规则约简以及判定表处理性能等方面提出了不少方法.

张福源团队、王立荣团队和张永强的工作虽然属于软件测试范畴，但是他们研究的测试用例技术是由因果图借助判定表生成测试用例，这实质上就是借助判定表获取输入（处理）逻辑.张福源团队和王立荣团队分别提出了由因果图生成判定表的算法和改进算法，提高了判定表的生成效率[3-4]；张永强提出了基于粗糙集理论的判定表约简步骤和方法，简化了判定表的归并和优化过程[5]；C.Grana团队提出减小判定表大小来降低复杂度的方法[6].他们对判定表的定义进行了扩充，提出了或判定表（OR-decision table）的概念，将传统的判定表称为与判定表（AND- decision table），通过把与判定表中相同的动作合并形成或判定表以达到降低判定表大小的目的.Phaisarn Sutheebanjard等人提出了将或判定表快速转换为判定树的算法，通过加快判定表转化为判定树的过程来提高处理的性能[7].

国防科技大学谢红卫等人[8]在故障树分析软件MFTA的开发中采用字符串表格组件实现判定表的直接输入，实现了系统内逻辑关系的动态变化.这对于问题2）的解决提供了一种独特的思路.除此之外，业务处理管理领域的工作也涉及判定表的应用研究，成果主要是给出应用判定表获取和编辑商业逻辑的方法和步骤[9-10].同时，有软件公司开发出了基于判定表的业务逻辑管理软件，如IBM公司的WebSphere ILOG JRules BRMS①IBM® WebSphere® ILOG® JRules BRMS 版本7.1文档.参见：http：//pic.dhe.ibm.com/infocenter/brjrules/v7r1/index.jsp?topic=％2Fcom.ibm.websphere.ilog.jrules.doc％2FContent％2FBusiness_Rules％2FDocumentation％2F_pubsk el％2FJRules％2Fps_JRules_Global510.html.，Catalyst development公司的LogicGem②LogicGem 3.0（Logic Processor and Decision Table Analysis Tool）.参见：http：//www.catalyst.com/products/logicgem/index.html.等，在其中能够灵活地编辑和管理规则，并对规则进行完备性检查，最后自动生成特定语言的业务规则程序源代码，这为信息系统的开发提供了极大的便利.但是，这些方法仍然采用的是传统的判定表形式和处理方法，不能很好地解决上述提及的2）和3）的问题.

遗憾的是鲜有文章专门探讨判定表在详细设计阶段存在的问题及改进，这似乎也印证了图灵奖得主Sifakis教授在CCF CNCC2011大会上的所讲，“在广大计算机科学研究人员的研究日程和计划上，系统设计并未得到足够的重视”[11].

为了完整解决上述问题，笔者依据集合论提出了一种全新的详细设计方法——N+2表法，该方法通过构造一张特定结构的二维表（本文称之为N+2表）以确立条件组合和动作之间的映射，从而方便快速地获取处理逻辑.这些处理逻辑表现为该二维表中的元组，因此对它的处理算法不再是复杂的多层多条件判断而是简单的行选择，从而使得处理算法简单高效.更为重要的是该方法使得条件组合、处理动作以及二者之间的映射独立于程序和算法，因而能够很好地实现处理逻辑动态变化的要求.

1 方法原理

根据集合论，每个条件可以看成是一个集合，该条件的所有取值就是该集合的元素.

定义1（条件集合） 如果条件D有m个取值，则条件D定义为一个基数为m的集合，条件D的诸个取值就是该条件集合的元素.

定义2（条件组合） 条件组合定义为：

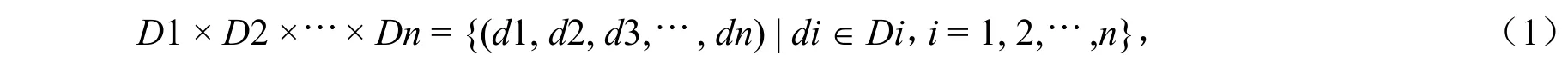
定义3（条件组合的总个数） 条件组合的总个数M定义为：

M等于各集合Di的基数之积.每一个动作或计算模型也可以看成是一个集合的元素，该集合就是动作或计算模型集合.每一个条件组合与一个动作或计算模型相关，一个动作或计算模型可以与多个条件组合相关，因此动作集合的基数k小于等于条件组合的总个数M.

定义4（动作或计算模型集合） 动作或计算模型定义为：

该集合的元素Aj可以表示每一个动作或计算模型.

对于复杂条件处理问题，如果能够确定条件组合和动作之间的映射关系就意味着获取了处理逻辑.借助上述定义可以明确：获取处理逻辑的实质就是找出上述公式（1）中笛卡尔集的每一元组（d1, d2, d3,?, dn）与公式（3）中动作或计算模型集合A中元素Aj存在的映射关系，也就是说，一旦能够表示出公式（1）和（3）的映射关系，也就获取了该问题的处理逻辑或处理规则.如果能够方便快速地表达公式（1）和（3）的映射关系就能实现快速获取处理逻辑.

借助上述定义还可以看到：处理逻辑发生变化，其实质就是公式（3）中某个动作或计算模型元素发生变化或是公式（1）和（3）的映射发生改变，如果能够不修改源程序就能实现二者的改变，就能实现处理规则的动态改变.

由于笛卡尔集可以表示为一个二维表[12]，因此，本文提出一种基于二维表的方法来解决传统判定表方法在复杂条件情况下存在的问题.

2 N+2表法

由于笛卡尔集可以表示为一个二维表，因此公式（1）定义的n个条件的条件组合可以用一张n列二维表表示，表中的一列表示一个条件集合，一行（即元组）表示条件的一个组合.为了提高处理性能，将该二维表再增加2列，一列表示公式（3）定义的动作集合，另一列用于表示条件组合的编码.由此构造的这个n+2列二维表本文称之为N+2表，如表2所示.基于N+2表进行复杂条件处理的详细设计方法本文称之为N+2表法.

表2 N+2表的结构

下面详细介绍该方法中N+2表的构造、处理逻辑实现算法和方法步骤.

2.1 N+2表的构造

根据需求，如果问题域中涉及的条件有n个，那么N+2表的结构就为n+2列的二维表.第1列到第n列对应n个条件，第n+1列存放动作或计算模型，第n+2列存放条件组合编码.该条件组合编码是一个n位编码，每位代表一个条件的某个取值，每一条件取值用一位编码表示，编码规则由设计人员自主定义.假定最高位为第一位，第一位代表第一个条件的某个取值，第二位代表第二个条件的某个取值，以此类推，由此可由该编码唯一标识一个条件组合的取值，也就是该N+2表的一行元组.

我们可以根据需求将各条件的组合和动作添加到该N+2表中，其中每行元组包括n列的条件组合信息、1列的动作信息和1列的条件组合编码.显然，得到了这个二维表中各元组数据实质上就是获得了条件组合和动作二者的对应关系，即获得了公式（1）和（3）的映射，这其实就是获得了该复杂条件判断的处理逻辑.

表3 判断二维表结构示例

例如：某处理涉及性别、年龄、学历、婚否4个条件，则构造的N+2表是一个6（4+2）列的二维表，如表3所示.表3前4列对应4个条件，第5列存放动作或计算模型，第6列存放4位条件组合编码，分别表示性别、年龄、学历、婚否四个条件的某个取值.假定条件取值编码规则为“性别”条件取值为“男”用“1”表示，“年龄”条件取值在30 – 39岁之间用“c”表示，“学历”条件取值为本科用“5”表示，“婚否”条件取值为已婚用“1”表示，那么，“性别为男、年龄在30 – 39岁之间、学历为本科、婚否为已婚”这一条件组合编码则为“1c51”.

2.2 处理逻辑实现算法

构造了上述的N+2表后，就可以根据需求将各条件及其动作以元组（行）的方式插入到表中.N+2表中的所有元组实质上就是该复杂条件判断问题的处理逻辑，此时，要实现这个处理逻辑将不再需要多层嵌套的多条件判断，而只需用简单的行选择算法，即逐行扫描N+2表以寻找与输入的条件组合编码相同的元组（行）即可，如果找到，则该元组的动作或计算模型就是所需结果，如果没有找到，则说明处理规则还需要补充，可以给出提示.

基于N+2表的复杂条件处理算法如图1所示.图1中t[i]表示N+2表中的第i行元组，“t[i]条件编码”表示该表中第i行元组的条件编码的分量值.

如果采用RDBMS建立上述N+2表，上述处理的实现将变得更加简单，我们就可以直接使用RDBMS提供的元组增、删、改操作获取处理逻辑，使用“SELECT-FROM-WHERE”查询语句实现处理.同时，处理逻辑表现为二维表中的元组，通过修改元组数据就可以方便实现处理逻辑的改变，这时处理逻辑的改变是独立于程序和算法的，因而不需修改源程序就能实现处理逻辑的动态改变.

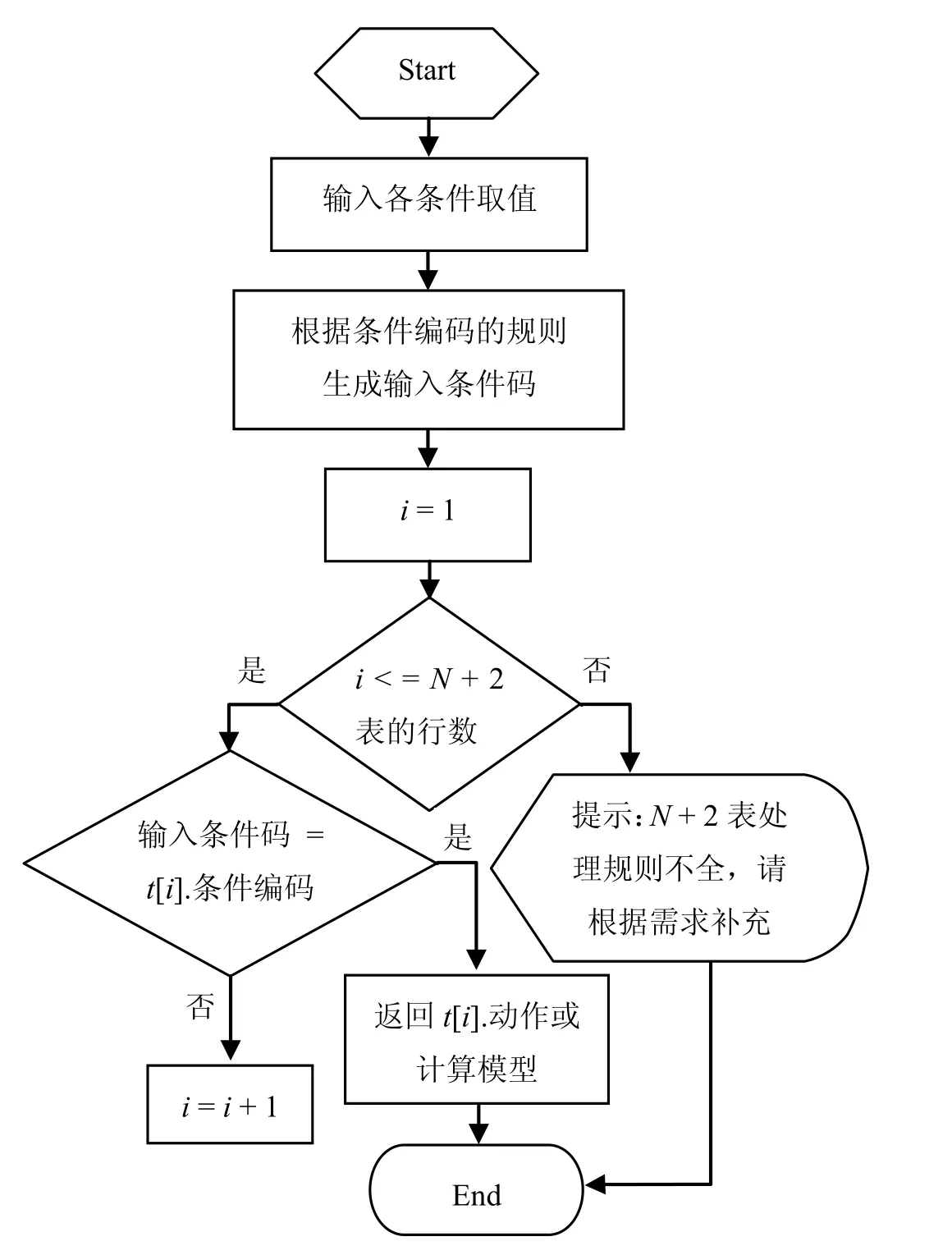
图1 基于判定二维表的复杂条件处理算法

2.3 N+2表法方法步骤

针对复杂条件处理的详细设计，可以应用N+2表法进行，其主要步骤如下：

第一步：分析、整理处理涉及的条件及其数量，条件的总个数即为n；

第二步：构造N+2表，即构造n+2列的二维表，前n列存放n个条件的取值，第n+1列存放动作或计算模型，第n+2列存放条件组合编码，该条件组合编码是一个n位编码，每位代表一个条件的某个取值，每一条件取值用一位编码表示，编码规则由设计人员自主定义，条件组合编码唯一标识每个条件组合，是N+2表的主键；

第三步：列出每个条件的不同取值，用1位编码表示，编码规则自定；

第四步：建立该N+2表（可在RDBMS中建立）；

第五步：根据需求将各条件及其动作以元组（行）的方式插入到表中，每行元组表示一个处理逻辑或处理规则；

第六步：根据2.2中给出的算法编码.

3 应用实例

笔者在研发某高校宣传奖励综合信息系统时应用上述N+2表法简便高效地解决了复杂条件处理问题.该系统是涵盖高校对外宣传奖励工作全业务过程的管理信息系统，功能包括作品收录、作品审核、作品奖励、作品归档、调档查询、奖励规则设置等，其中的奖励计算和奖励规则设置功能是系统的核心功能。奖励计算功能要求按照奖励规则对已经通过审核的作品自动进行奖励计算，奖励规则涉及的因素（条件）有9个，分别是作者的单位部门、媒体级别、媒体类型、作品类型、作者身份、报刊版面、文字字数、作品时长以及是否批阅转发，而每个条件又有多种不同的取值，奖励规则设置功能则要求实现每年都能改变部分具体的奖励规则.

该奖励部分涉及的条件有9个之多，每个条件的取值少则3个，多则9个，如果采用传统设计方法，不仅构造判定表困难重重，容易出错，而且随后要快速得到清晰的处理逻辑也是非常困难的，更致命的是无法简便地实现奖励规则的动态变化.

在上述功能的详细设计过程中，我们按照2.3所述的N+2表方法步骤，构造了2.1所述的N+2表，如表4所示.该奖励计算涉及的条件有9个，因此该N+2表是11列（9+2）的二维表，其中前9列为9个条件，第10列是奖金数额或计算公式，第11列是9位数构成的条件组合编码（每位代表一个条件的某个取值），其中条件组合编码作为该表的键码.

表4 某高校宣传奖励综合信息系统奖励计算判定二维表

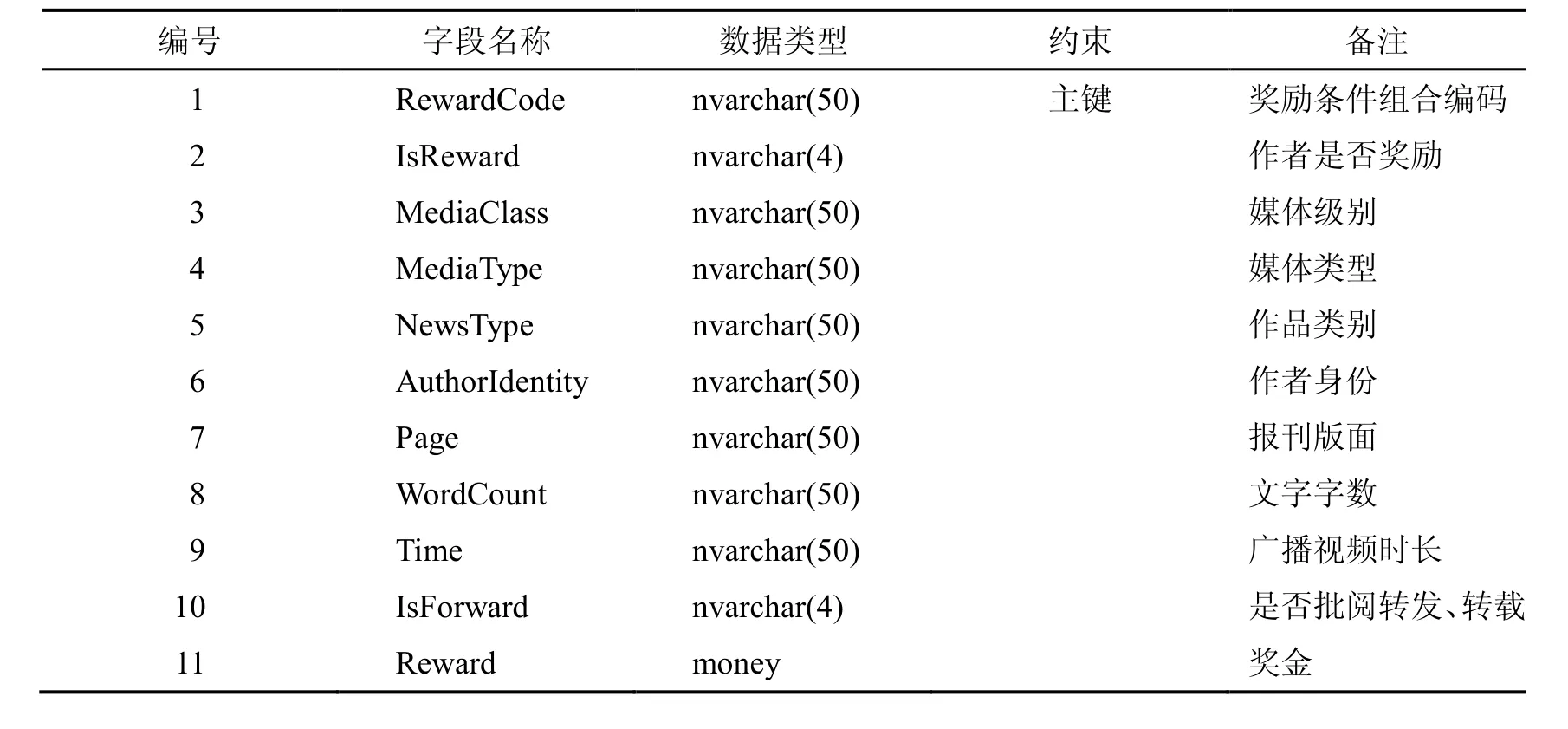
表5 奖励计算判定二维表逻辑结构

把上述二维表在RDBMS中创建，其逻辑结构如表5所示.之后，根据奖励文件（共有21页）将各条件组合、奖金金额和条件组合编码填入该二维表中，得到的二维表中的元组数据实质上就是奖励规则.奖励计算功能的实现按照2.2所述的算法，只需对表中的元组进行行扫描即可实现.这里直接使用RDBMS的SELECT-FROM-WHERE查询就可高效简便地实现，无须使用多层多条件判断.由于元组数据就是奖励规则，因此奖励规则设置功能实质就是对表中元组的增加、修改和删除，只要该二维表的结构不发生变化，也就是条件的种类不发生变化，那么仅仅通过增加、删除和修改二维表的元组数据就能方便地实现奖励规则的改变，而不需要修改算法和程序，真正实现了处理逻辑动态变化的要求.

4 结 论

本文依据集合论提出了N+2表法，通过构造特定结构的二维表N+2表快速获取复杂条件处理问题的处理逻辑，通过对该表的行扫描实现处理逻辑，通过对该表中元组的增、删、改操作实现处理逻辑的动态变化.自2011年6月起，笔者在多个应用系统的开发实践中应用该方法进行复杂条件处理的详细设计，实践表明，与传统详细设计工具相比，该方法在以下3方面有明显优势：

1）获取处理逻辑 为了将需求转变为较为清晰便于实现的处理规则，采用传统的判定表和判定树方法需要分析设计人员多次进行合并和转换以实现规则的约简，这使得处理逻辑的获取时间较长，同时也非常依赖于分析设计人员的经验.而N+2表方法只需经过简单的条件分析就能方便快速地构造出一张二维表形式的N+2表，这张二维表中的元组就是处理逻辑（规则），因此，不再需要依赖设计人员依据经验进行规则约简就能方便、迅速、直观地获取处理逻辑（规则）.

2）算法实现 传统的判定表和判定树为了实现处理逻辑（规则）需要多层多条件的复杂判断，这使得算法繁冗复杂，可读性和可维护性都较差，这也就是传统的判定表须进行多次合并和转换以进行规则约简的根本原因，目的在于降低判断的复杂度，增强程序的可读性和可维护性.而使用N+2法，二维表中的元组就是处理逻辑，实现处理逻辑时只需进行“行选择”即可，不仅算法简单，程序易实现，更为重要的是可以不必对众多规则进行约简，处理效率也较高.假设整个处理涉及5个条件，每个条件有4个不同取值，则条件的组合为45=1 024种，即至多应有1 024条处理规则才能完整涵盖整个处理，如果采用传统的判定表，为了获取处理加工逻辑，即使进行长时间约简，一般情况下算法的复杂程度也仍会十分惊人，但如果采用N+2表法，只需构造一张7列的二维表，其中的每一行即表示一个处理规则，要完整涵盖整个处理只需向表中添加1 024行规则即可，同时也不需进行规则约简，直接通过执行“行选择”操作就可以实现处理逻辑.

3）适应变化的能力 传统方法中，处理逻辑是嵌入在程序代码中的，因而，适应变化的能力很差，一旦处理逻辑发生变化，就必须修改源程序代码.尽管有一些商业软件能够进行规则或逻辑的管理、审查以至自动生成处理逻辑的源代码，但是，这些规则或逻辑仍然是嵌入到源代码中的，也无法实现处理逻辑的动态改变要求.而N+2表法中的处理逻辑就是二维表的元组，因此，这些处理逻辑与关系数据库中的数据一样是完全独立于程序和算法的，只需通过增、删、改元组操作就能实现处理规则的动态改变，因而适应变化的能力强，很好地解决了传统工具无法实现规则动态变化的要求.

随着信息技术在各领域的应用普及，各类应用系统研发的数量日益增多，系统要求也日益提高，这就要求我们勇于对传统的软件工程方法和技术进行改进和创新，从而推动软件工程持续不断的发展.

[1] 张海藩.软件工程导论[M].第五版.北京：清华大学出版社, 2008：117-118.

[2] Codasyl.A Modern Appraisal of Decision Tables：Report of the Decision Table Task Group [R].New York：ACM, 1982：2-4.

[3] 张福源, 杨云.基于因果图的软件测试工具的研究与设计[J].计算机学报, 1993, 16（3）：219-224.

[4] 王立荣, 何炜.基于因果图的软件测试方法[J].计算机系统应用, 2010, 19（4）：104-107.

[5] 张永强, 刘彦瑞.基于粗糙集的因果图方法简化研究[J].计算机技术与发展, 2006, 16（7）：42-44.

[6] Grana C, Borghesani D, Cucchiara R.Optimized block-based connected components labeling with decision trees [J].IEEE Transactions on Image Processing, 2010, 19（6）：1596-1609.

[7] Sutheebanjard P, Premchaiswadi W.Fast Convert OR-Decision Table to Decision Tree [C] //Sterritt R.2010 Eighth International Conference on ICT and Knowledge Engineering.New York：IEEE, 2010：37-40.

[8] 谢红卫, 夏家海, 张明.基于立方体理论的MFTA软件设计与实现[J].国防科技大学学报, 2000, 22（15）：99-102.

[9] Auechaikul T, Vatanawood W.A Development of Business Rules with Decision Tables for Business Processes [C] //Sterritt R.TENCON 2007-2007 IEEE Region 10 Conference.New York：IEEE, 2007：1-4.

[10] Thirumaran M, Dhavachelvan P, Subhashree S.Business Rule Management Framework for N-Tier E-Business Applications [J].International Journal of Managing Public Sector Information and Communication Technologies, 2010, 1（1）：1-14.

[11] Sifakis J.GreenOrbs绿野千传项目组译.计算机科学的愿景：系统发展观[J].中国计算机学会通讯, 2012, 8（3）：11-18.

[12] 王珊, 萨师煊.数据库系统概论[M].第四版.北京：高等教育出版社, 2006：41-44.

The Detailed Design Method for Complicated Multi-conditions Process of Application Software —— N+2 Table

WANG Yong
（School of Physics and Electronic Information Engineering, Wenzhou University, Wenzhou, China 325035）

During the development of application software, many problems will occur when using traditional tools in detailed design stage of complicated multi-conditions process.A new method called ―N+2 table” is then proposed on the basis of set theory in this paper.With the method, a particular two-dimensional table, N+2 table, is constructed to acquire process logics rapidly.When programming process logics, the algorithm of row-scanning is adopted instead of nested multi-layer ―IF-THEN-ELSE” structures.Furthermore, the method makes independent of algorithm the combinations of conditions, actions and the mapping between them.Thus it makes the dynamic changes of process logics come true just by inserting, deleting and updating tuples.The method has been applied to the development of some application system.Practice indicates that it has obvious advantages over the traditional methods.

Complicated Multi-conditions Process；Detailed Design Method；N+2 Table

TP311.52

A

1674-3563（2013）04-0032-08

10.3875/j.issn.1674-3563.2013.04.006 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2013-03-01

王咏（1968- ），女，湖北武汉人，高级工程师，硕士，研究方向：软件工程，商务智能