最小一乘估计性质的讨论

寇桂晏，陈希镇

（温州大学数学与信息科学学院，浙江温州 325035）

最小一乘估计性质的讨论

寇桂晏，陈希镇†

（温州大学数学与信息科学学院，浙江温州 325035）

解决某些问题时，最小一乘准则在很大程度上优于最小二乘准则.通过对最小一乘准则与最小二乘准则的比较分析，给出了最小一乘估计的一些优良性质，如无偏性、渐近正态性、有效性等，并做了相应的理论证明.

最小一乘法；无偏性；渐近正态性；有效性

在实际问题的分析中，常常需要研究某一现象与影响它的某一最主要因素的关系.针对类似问题，我们常常会建立相应的数学模型，然后对模型中的参数进行估计.普通最小二乘方法（OLS）是常用的参数估计方法，由于它在正态分布模型中表现出很好的性质，故随着正态模型的广泛应用而发展得比较成熟和完善.但是，当测量数据中存在噪声时，特别地，当所作的拟合有较大干扰的尖峰时，应用最小二乘法得到的参数精度不高，因为当尖峰突出时，其误差平方值相对更大，为了降低平方和，需要将就这些奇异点，因而残差本身大的数据对参数的影响就更大了，从而使参数估计的精度大大降低.最小一乘法受异常值的影响相对于最小二乘法要小，具有良好的稳健性[1-3].但最小一乘准则有一个主要不足 —— 准则函数不可微，不能很好地利用已有的非线性规划方法来快速搜索其最优解，所以很长一段时间，最小一乘法处于停滞状态.现在，随着计算机科学的发展，有关寻找它最优解的算法也越来越易于实现，且计算速度快，精度高[4]，因此，最小一乘法在理论和应用中都越来越受重视.

实际上，从统计学的发展史来看，拉普拉斯提出最小一乘法比高斯提出最小二乘法要早，1961年，Walter D.Fisher在文献[5]中就给出了线性模型中的最小一乘曲线拟合；此后，陈希孺在文献[1]和文献[2]中分别讨论了在一维和多维情况下，最小一乘估计的本质，即其最优解为中位数.人们通常假定回归模型中的随机误差服从正态分布，在这种假设下，最小二乘估计有一些好的性质，但某些数量经济模型涉及的随机误差不具有正态性，而是服从某种厚尾分布，且方差可能是无限的，在这种情况下，最小一乘估计的统计性能优于最小二乘估计[1-2]，最小一乘准则拟合图形更接近于人的直觉.本文将给出最小一乘估计的一些优良性质，并对相应的理论给出证明.

1 最小一乘准则

假设给定n 个样本点（x1,y1），（x2,y2），…，（xn,yn），其中yi∈R1，xi∈Rm，i=1,2,…,n，现将由这些数据拟合一个超平面方程y=xβ′，并使参数β满足偏差绝对值之和最小，其中β=（β0,β1,β2,…,βm）∈Rm+1为待估计的参数，上标一撇表示向量的转置.

2 最小一乘估计的定理及一些优良性质的证明

由于最小一乘法的以上几种优点，且基于现代计算机编程能力的快速发展，对最小一乘的最优解也更容易实现了，所以现在最小一乘法应用相当广泛.为了便于以后最小一乘的应用，下面给出并证明最小一乘所具有的良好的数学性质：无偏性、渐近正态性、有效性等.

2.1 最小一乘估计的定理

定理1 设Y服从某连续型分布，并记g（y）为其密度函数，则使达到最小的解是Y的中位数p.

证明：由于

为使f（m）达到最小，则应满足一阶导数条件f′（m）=0，因此对上式求导得：

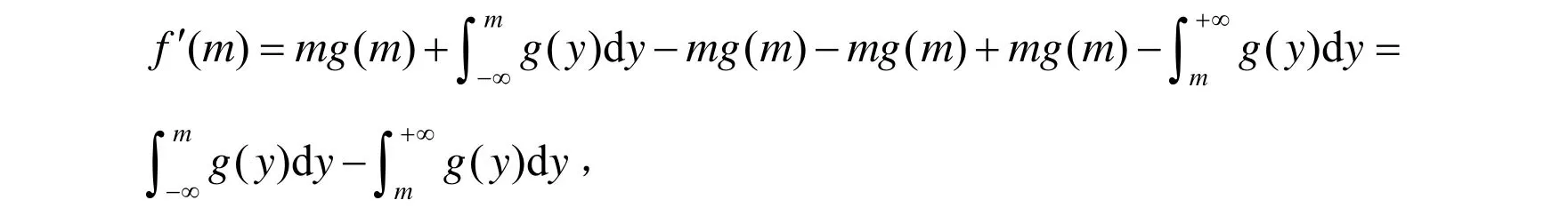
满足上述方程的m 即为Y的中位数p.验证二阶导数条件：

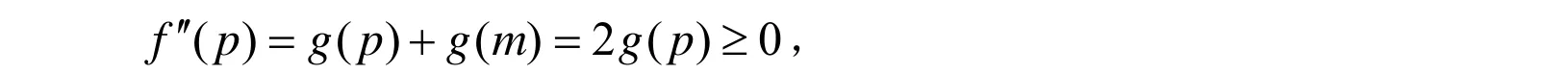
定理2 设Y具有某离散型分布，则使达到最小值的是中位数ymed.

证明：对Y进行排序得y1≤y2≤…≤yn有序数列.不妨设m=yk使得达到最小值.令J（k）=由于yk-yk+1≤0，当时，J（k ）-J（k +1）≥0，当 时，J（k ）-J（k +1）≤0，故只有在时取得最小值，即为样本中位数时，

达到最小.定理得证.

2.2 参数及其估计

一般地，任何定义在Θ上的实值函数都可以称为参数，但参数的定义不止参数统计结构中有，在非参数、半参数统计结构中也同样有.

定义在P={Pθ：θ∈Θ}上的一个实值泛函g（P）称为参数，而（Y,B,P）上的用来估计g（P）的实值统计量称为g（P）的点估计量，简称估计.

由上述定义看出，估计的概念应用相当广泛，针对相应的模型都可以给出估计，如果不对估计的好坏加以明确，参数的估计就失去了意义.下面将讨论估计的好坏标准.为了寻找参数的一个好的估计，首先对估计提出一些合理性要求，把不合理的估计排除在外，然后在满足这种合理性要求的估计类中找到好的估计.最常用的一种合理性要求便是无偏性.

2.2.1 无偏性

定义1 设（Y,B,P）为可控参数统计结构，其中，P={Pθ：θ∈Θ}，g（θ）是未知参数，Y= （Y1,…,Yn）是来自该统计结构的一个样本，若用ˆ（Y）估计g（θ），且Eθ（ˆ（Y））=g（θ），∀θ∈Θ，则称ˆ（Y）为g（θ）的无偏估计.

通过下面的例子，给出最小一乘估计的无偏性.

例1 若总体Y～N（μ,σ2），Y1,Y2,…,Yn为Y的一个样本，证明为σ的无偏估计.

证明：因为

并且由总体Y的分布可得：

此性质通过样本平均绝对偏差引进了正态分布标准差σ的一个无偏估计，即最小一乘估计具有无偏性.无偏性体现了一种频率思想，只有在大量重复使用时，无偏性才有意义.

下面将证明最小一乘估计在大样本场合所具有的渐进性质.

2.2.2 渐近正态性

下面通过例2给出有关最小一乘估计的渐进正态性.

例2 i）若总体Y的密度函数为f（y），其中位数为p，且f（p）≠0，而Y1,Y2,…,Yn为它的一个样本，其样本中位数为Ymed，则Xn=n（Ymed-p）的极限分布为N（0,1/[4（f2（p ）]）；

ii）若总体Y～N（μ,σ2），而Y1,Y2,…,Yn为它的样本，Ymed为其中位数，则Ymed的分布渐近于N（μ,πσ2/2n）.

证明：i）记g（ymed）为Ymed的密度函数，设n为奇数，由次序统计量的密度函数公式可得：

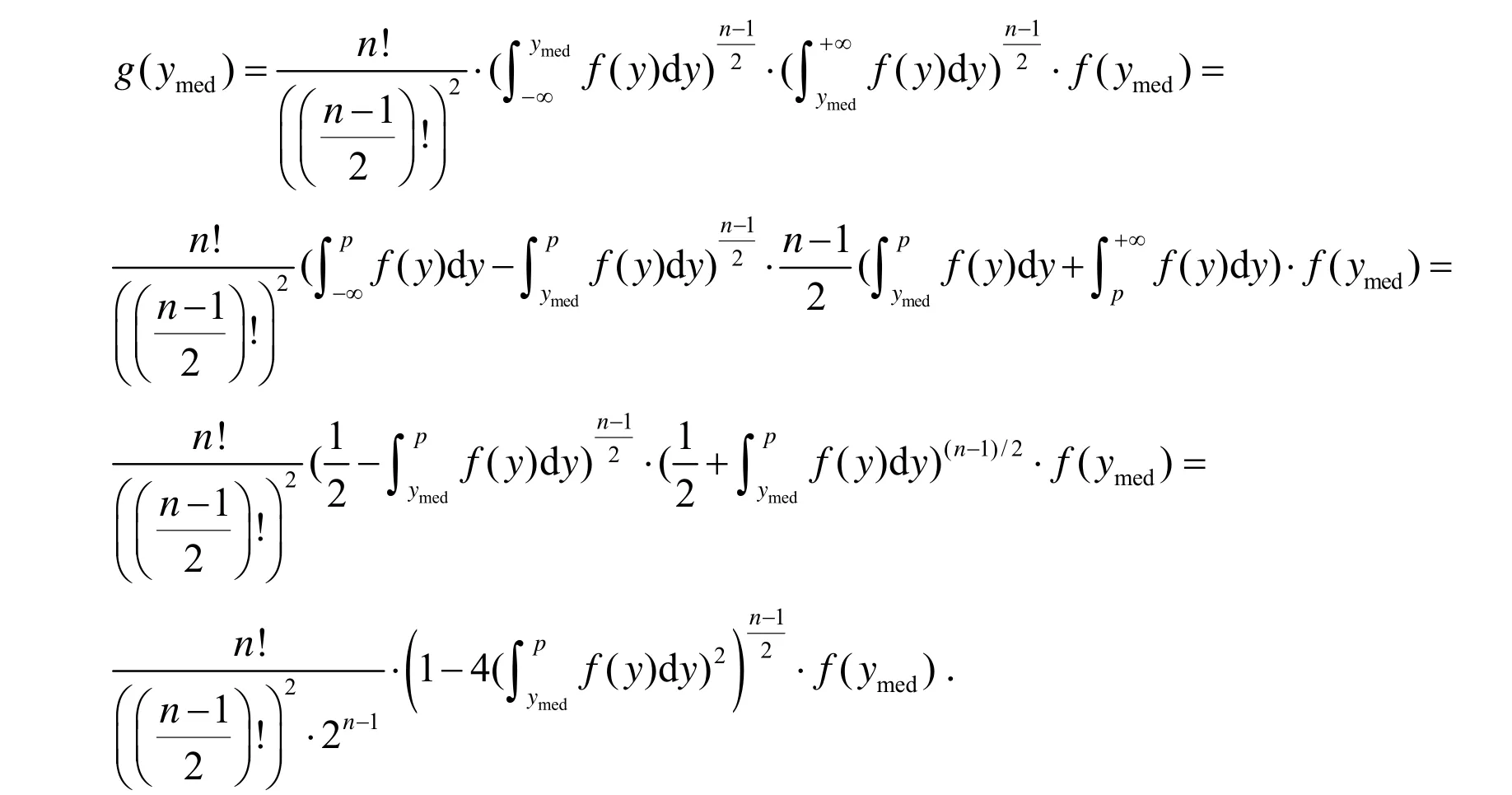
设Xn的密度函数为hn（x），则有：

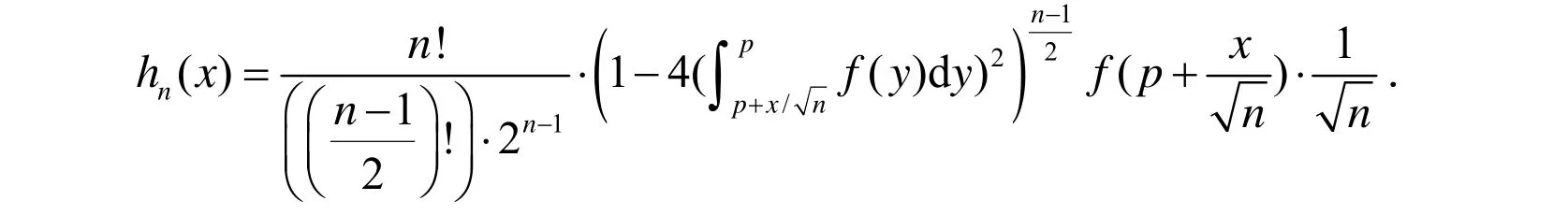
一方面，当n→∞时，有：

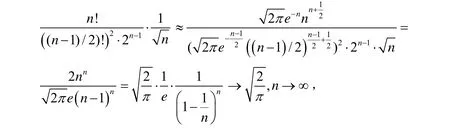
所以，当n→∞时，有hn（x）→，即X=n（Y-p）的极限分布为n med

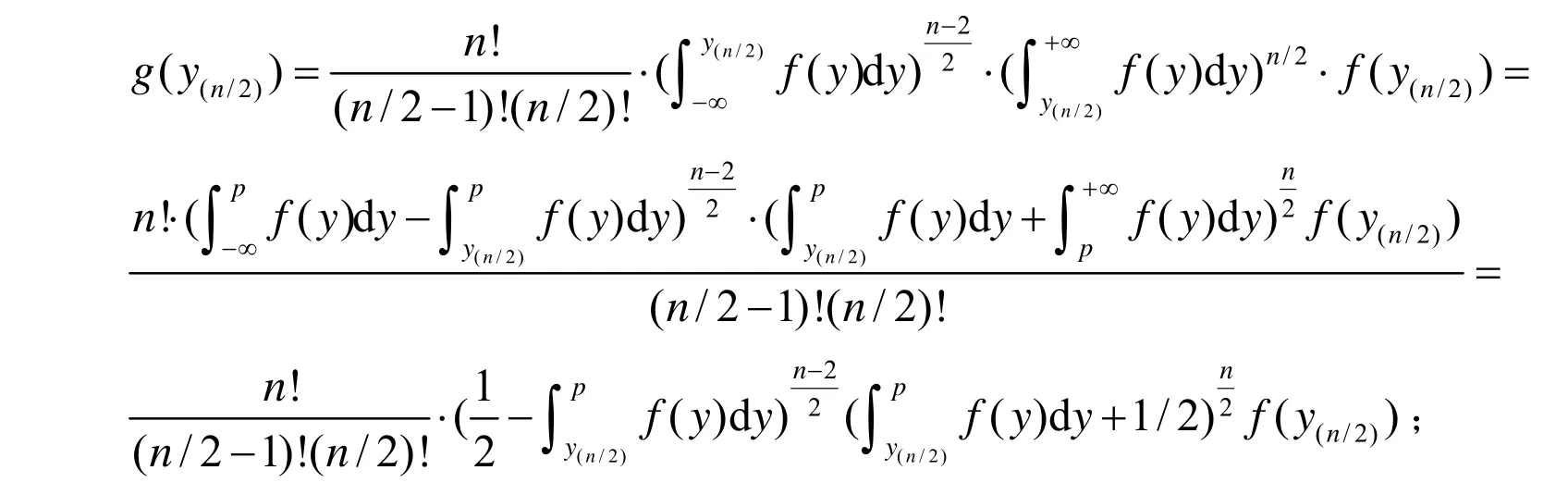
次序统计量Y（n/2+1）的密度函数为：

由于密度函数是连续的，所以有：

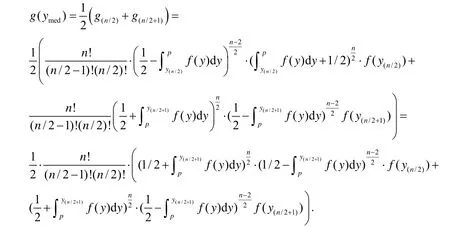
Xn的密度函数hn（x）同样经过重要极限和Stirling公式可以得出：当n→∞时，有hn（x）→即Xn=n（Ymed-p）的极限分布为

ii）在正态N（μ,σ2）场合，，p=μ，f（p）=f（μ）=1/（2πσ）≠0，这时Ymed的分布渐近于即导出了一般场合及正态场合样本中位数的渐近分布.

2.2.3 有效性

有些正则条件下的分布族中参数的无偏估计的C-R下界可以达到，有些则不能.我们将达到C-R下界的无偏估计称为有效无偏估计，将无偏估计的方差与其C-R下界之比的倒数称为该估计的效[6].

定义3 设{Pθ（Y ）：θ∈Θ}是Cramer-Rao正则族，g（θ）是可估参数，ˆ（Y）是g（θ）的一个无偏估计，则称为估计ˆ（Y）的效，如果效等于1，则称ˆ（Y）为g（θ）的有效无偏估计.

证明：由于lnf（y,μ）=-lnπ-ln[1+（y -μ）2]，，可求得Fisher信息：I（μ）=因此，参数μ的估计量方差的C-R下界为.又由

2.2.2 知，柯西分布总体的一个容量为n 的样本中位数Y渐近服从N（μ,π2/4n），因此这个估med计量的渐近有效率为：

所以，对厚尾分布之一的柯西分布，在估计参数μ时，样本中位数Ymed比样本均值优胜得多.

3 结 语

最小二乘法的优点在于其有良好的数学性质，它的理论基础是希尔伯特空间的投影理论，基于该空间理论的完备性，对于最小二乘数值求解比较容易，因此，该方法已广泛应用于各种领域.但是，最小二乘估计容易受异常值的影响.本文证明了最小一乘估计的一些优良性质，因为最小一乘准则所考虑的是残差的一次方并非平方，因此受异常值的影响小得多，故它具有比最小二乘准则更好的稳健性，但在样本容量n较大时，计算比较复杂[3].现在，已经可以通过Lingo10、Matlab等计算机软件实现最小一乘最优解的快速计算[4].我们相信随着相关算法的计算机实现，最小一乘法会得到更为广泛的应用.

[1] 陈希孺.最小一乘线性回归：上[J].数理统计与管理, 1989, （5）：48-55.

[2] 陈希孺.最小一乘线性回归：下[J].数理统计与管理, 1989, （6）：48-56.

[3] 李仲来.最小一乘法介绍[J].数学通报, 1992, （2）：42-45.

[4] 吕书龙, 刘文丽.最小一乘估计快速算法[J].应用概率统计, 2008, （12）：621-630.

[5] Fisher W D.A note on curve fitting with minmum deviations by linear programming [J].Jiurnal of American Statistical Association, 1961, （56）：359-361.

[6] 茆诗松, 王静龙, 濮晓龙.高等数理统计[M].第二版.北京：高等教育出版社, 2006：98-107.

A Discussion on the Properties of the Least Absolute Deviation Estimator

KOU Guiyan, CHEN Xizhen
（School of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035）

In addressing certain issues, the criterion of the Least Absolute Deviation is better than that of the Least Square Method to a large extent.After the contrastive analysis between the criterion of the Least Absolute Deviation and that of the Least Square Method, some of the good properties of the Least Absolute Deviation are given, such as unbiased property, asymptotic normality properties, effectiveness, and so on, which are then proved theoretically.

Least Absolute Deviation；Unbiased Property；Asymptotic Normality Properties；Effectiveness

O212

A

1674-3563（2013）04-0005-07

10.3875/j.issn.1674-3563.2013.04.002 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2013-01-30

寇桂晏（1989- ），男，江西上饶人，硕士研究生，研究方向：应用统计.† 通讯作者，kgy0207@163.com